Напиши пару

Пара Туси (также известная как механизм Туси) [1] [2] [3] ) — математический аппарат, в котором маленький круг вращается внутри большего круга, диаметр которого в два раза превышает диаметр меньшего круга. Вращение кругов приводит к тому, что точка на окружности меньшего круга колебания вперед и назад совершает линейные вдоль диаметра большего круга. Пара Туси представляет собой двухбугорную гипоциклоиду .
Пара была впервые предложена персидским астрономом и математиком 13-го века Насир ад-Дином ат-Туси в его Тахрир аль-Маджисти (Комментарий к Альмагесту) 1247 года как решение проблемы широтного движения нижних планет. [4] и позже широко использовался в качестве замены экванта, введенного более тысячи лет назад в Птолемея » «Альмагесте . [5] [6]
Исходное описание
[ редактировать ]

Перевод копии оригинального описания его геометрической модели Туси намекает по крайней мере на одну инверсию модели, которую можно увидеть на диаграммах:
- Если две компланарные окружности, диаметр одной из которых равен половине диаметра другой, считать внутренне касающимися в одной точке, и если на меньшей окружности взять точку — и пусть она будет в точке касания - и если два круга движутся простыми движениями в противоположном направлении таким образом, что движение меньшего [круга] в два раза больше, чем движение большего, так что меньший совершает два оборота за каждый оборот большего, тогда эта точка будет Видно, что он движется по диаметру большего круга, который первоначально проходит через точку касания, колеблясь между конечными точками. [8]
Описание не является последовательным и, по-видимому, произвольно сочетает в себе черты нескольких как возможных, так и невозможных инверсий геометрической модели.
Алгебраически модель можно выразить комплексными числами как
Другие комментаторы заметили, что пару Туси можно интерпретировать как катящуюся кривую , где вращение внутреннего круга удовлетворяет условию прилипания, поскольку его точка касания движется вдоль фиксированного внешнего круга.
Другие источники
[ редактировать ]
Термин «пара Туси» — современный термин, придуманный Эдвардом Стюартом Кеннеди в 1966 году. [9] Это одно из нескольких позднеисламских астрономических устройств, имеющих поразительное сходство с моделями из Николая Коперника » «О революции , включая его модель Меркурия и его теорию трепета . Историки подозревают, что Коперник или другой европейский автор имел доступ к арабскому астрономическому тексту, но точная цепочка передачи пока не установлена. [10] Ученый и путешественник XVI века Гийом Постель был предложен в качестве одного из возможных координаторов. [11] [12]
Поскольку пара Туси использовалась Коперником в его переформулировке математической астрономии, существует растущее согласие в том, что он каким-то образом осознал эту идею. Было предложено [13] [14] что идея четы Туси, возможно, пришла в Европу, оставив мало рукописных следов, поскольку она могла возникнуть без перевода какого-либо арабского текста на латынь. Один из возможных путей передачи мог проходить через византийскую науку ; Григорий Хиониад перевел некоторые произведения ат-Туси с арабского на византийский греческий язык . Несколько византийских греческих рукописей, содержащих пару Туси, до сих пор сохранились в Италии. [15]
Существуют и другие источники этой математической модели преобразования круговых движений в возвратно-поступательные линейные движения. Встречается в комментарии Прокла к первой книге Евклида. [16] и эта концепция была известна в Париже к середине 14 века. В своих вопросах о Сфере (написанных до 1362 года) Николь Орем описала, как объединить круговые движения для создания возвратно-поступательного линейного движения планеты по радиусу ее эпицикла. Описание Орема неясно, и неясно, представляет ли оно собой независимое изобретение или попытку разобраться с плохо понятным арабским текстом. [17]
Более поздние примеры
[ редактировать ]Хотя пара Туси была разработана в астрономическом контексте, позже математики и инженеры разработали аналогичные версии того, что стало называться гипоциклоидными прямолинейными механизмами. Математик Джероламо Кардано разработал систему, известную как движение Кардана (также известное как карданная передача ). [18] Инженеры девятнадцатого века Джеймс Уайт, [19] Мэтью Мюррей , [20] как и более поздние конструкторы, разработали практическое применение гипоциклоидного прямолинейного механизма.
Практичная и механически простая версия пары Туси, в которой отсутствует использование внешней зубчатой передачи, была разработана в 2021 году Джоном Гудманом для обеспечения линейного движения. [21] [ не удалось пройти проверку ] [ сомнительно – обсудить ] В нем используются 3 стандартные цилиндрические шестерни. Вращающийся (синий) рычаг установлен на центральном валу, к которому прикреплена фиксированная (желтая) шестерня. (Красная) промежуточная шестерня на рычаге входит в зацепление с неподвижной шестерней. Третья (зеленая) шестерня входит в зацепление с натяжным роликом. Третья шестерня имеет вдвое меньше зубьев, чем неподвижная шестерня. К третьей передаче прикреплен рычаг (оранжевый). Если длина рычага равна расстоянию между фиксированной и внешней шестернями = d, то рычаг будет описывать прямую линию броска = 2d. Преимущество этой конструкции состоит в том, что при использовании стандартных модульных шестерен, которые не обеспечивают требуемого хода, промежуточная шестерня не обязательно должна быть коллинеарна двум другим шестерням.
Гипотрохоид
[ редактировать ]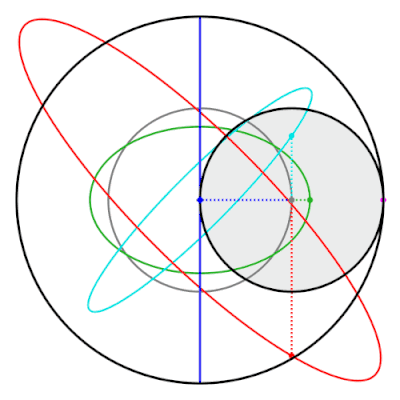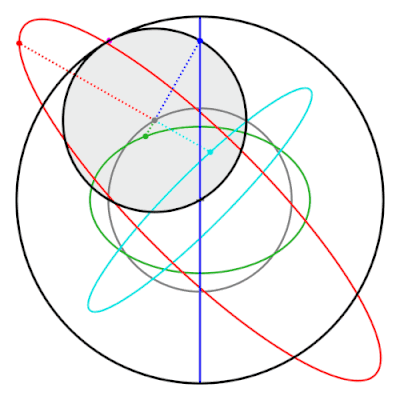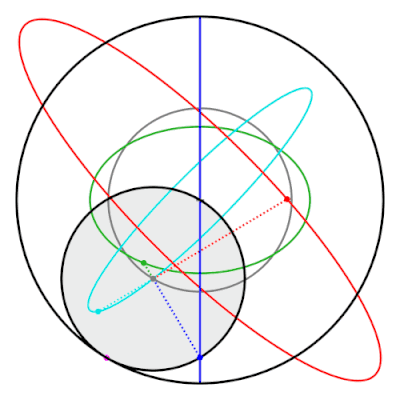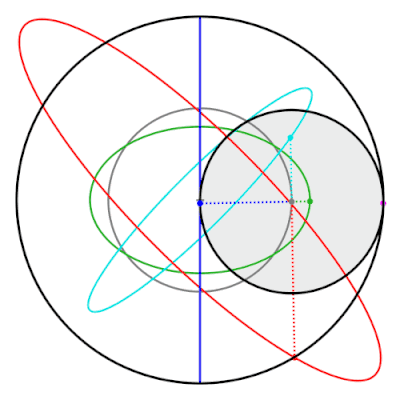
Свойством пары Туси является то, что точки на внутренней окружности не входят в эллипсы окружностей . Эти эллипсы и прямая линия, проведенная классической парой Туси, представляют собой частные случаи гипотрохоидов . [22]
См. также
[ редактировать ]- Гипоциклоидальный двигатель Мюррея , в котором используется пара Тузи вместо направляющих крейцкопфа или параллельного движения.
- Эпициклическая передача
- Прямолинейный механизм
- Спирограф
- Геометрический токарный станок
- Гильош
- Дельтовидная кривая
Примечания
[ редактировать ]- ^ Рошди Рашед (ред.). Энциклопедия истории арабской науки .
- ^ Салиба, Джордж (1 июля 2002 г.). «Греческая астрономия и средневековая арабская традиция: средневековые исламские астрономы были не просто переводчиками. Возможно, они также сыграли ключевую роль в революции Коперника» . Американский учёный . 90 (4): 360–368. дои : 10.1511/2002.27.360 .
- ^ Носоновский, Михаил (14 августа 2018 г.). «Абнер Бургосский: недостающее звено между Насир ад-Дином ат-Туси и Николаем Коперником?» . Зутот . 15 (1): 25–30. дои : 10.1163/18750214-12151070 . ISSN 1571-7283 . S2CID 135358186 .
- ^ Джордж Салиба (1995), « История арабской астрономии: планетарные теории во время золотого века ислама », стр. 152–155.
- ^ «Позднесредневековая планетарная теория», Э.С. Кеннеди, Isis 57 , № 3 (осень 1966 г.), 365–378, JSTOR 228366 .
- ^ Крейг Г. Фрейзер, « Космос: историческая перспектива », Greenwood Publishing Group, 2006, стр. 39.
- ^ Библиотека Ватикана, Ват. ар. 319 фол. 28 оборотная сторона math19 NS.15. Архивировано 24 декабря 2014 г. в Wayback Machine , копия рукописи из Туси четырнадцатого века.
- ^ Переведено в Ф. Дж. Рагепе, Мемуары по астрономии II.11 [2], стр. 194, 196.
- ^ Э.С. Кеннеди, «Планетарная теория позднего средневековья», с. 370.
- ^ Э.С. Кеннеди, «Планетарная теория позднего средневековья», с. 377.
- ^ Салиба, Джордж (1996), «Написание истории арабской астрономии: проблемы и разные точки зрения», Журнал Американского восточного общества , 116 (4): 709–18, doi : 10.2307/605441 , JSTOR 605441 , стр. 716- 17.
- ^ Чья наука является арабской наукой в Европе эпохи Возрождения? , Джордж Салиба Колумбийский университет
- ^ Клаудия Крен, «Катающееся устройство», с. 497.
- ^ Джордж Салиба , «Чья наука - арабская наука в Европе эпохи Возрождения?» [1]
- ^ Джордж Салиба (27 апреля 2006 г.). «Исламская наука и становление Европы эпохи Возрождения» . Библиотека Конгресса . Проверено 1 марта 2008 г.
- ^ Веселовский И.Н. (1973). «Коперник и Насир ад-Дин ат-Туси» . Журнал истории астрономии . 4 (2): 128–30. Бибкод : 1973JHA.....4..128В . дои : 10.1177/002182867300400205 . S2CID 118453340 .
- ^ Клаудия Крен, «Катающееся устройство», стр. 490-2.
- ^ Веселовский И.Н. (1973). «Коперник и Насир ад-Дин ат-Туси». Журнал истории астрономии . 4 (2): 128–130. Бибкод : 1973JHA.....4..128В . дои : 10.1177/002182867300400205 . S2CID 118453340 .
- ^ «Словарь Эпплтона по машинам, механике, двигателестроению и технике» . 1857.
- ^ «Моделирование Полли: комплекты стационарных двигателей — модели Энтони Маунта» . Архивировано из оригинала 27 марта 2019 г. Проверено 30 декабря 2016 г.
- ^ «Уравнение времени – Введение» . уравнение-оф-времени.info . Проверено 4 сентября 2022 г.
- ^ Бранде, WT (1875), Словарь науки, литературы и искусства , Longmans, Green and Company, стр. 181 , получено 10 апреля 2017 г.
Ссылки
[ редактировать ]- Ди Боно, Марио (1995). «Устройство Коперника, Амико, Фракасторо и Туси: наблюдения по использованию и передаче модели». Журнал истории астрономии . 26 (2): 133–154. Бибкод : 1995JHA....26..133D . дои : 10.1177/002182869502600203 . S2CID 118330488 .
- Кеннеди, ЕС (1966). «Позднесредневековая планетарная теория». Исида . 57 (3): 365–378. дои : 10.1086/350144 . S2CID 143569912 .
- Крен, Клаудия (1971). «Вращающееся устройство Насира ад-Дина аль-Туси в De spera Николь Орем». Исида . 62 (4): 490–498. дои : 10.1086/350791 . S2CID 144526697 .
- Рагеп, Ф.Дж. «Две версии пары Туси», в книге « От почтительного к равному: том исследований по истории науки на древнем и средневековом Ближнем Востоке в честь Э.С. Кеннеди» , изд. Дэвид Кинг и Джордж Салиба, Анналы Нью-Йоркской академии наук, 500. Нью-Йоркская академия наук, 1987. ISBN 0-89766-396-9 (пбк.)
- Рагеп, Ф. Дж. Насир ад-Дин ат-Туси «Мемуары по астрономии», « Источники по истории математики и физических наук», 12. 2 тома. Берлин/Нью-Йорк: Springer, 1993. ISBN 3-540-94051-0 / ISBN 0-387-94051-0 .
Внешние ссылки
[ редактировать ]- Деннис В. Дьюк, «Анимация древних планетарных моделей» включает в себя две интересные ссылки:
- Джордж Салиба, «Чья наука - арабская наука в Европе эпохи Возрождения?» Обсуждает модель Насир ад-Дина ат-Туси и взаимодействие арабских, греческих и латинских астрономов.
