Гипотрохоид

Красная кривая представляет собой гипотрохоиду, нарисованную по мере того, как меньший черный круг вращается внутри большего синего круга (параметры: R = 5, r = 3, d = 5 ).

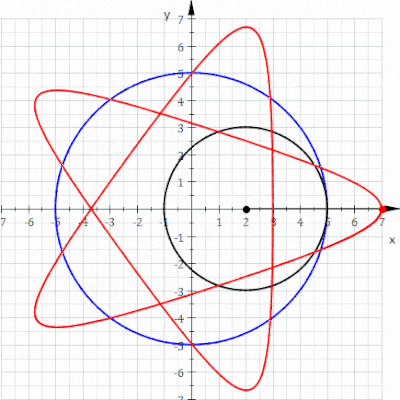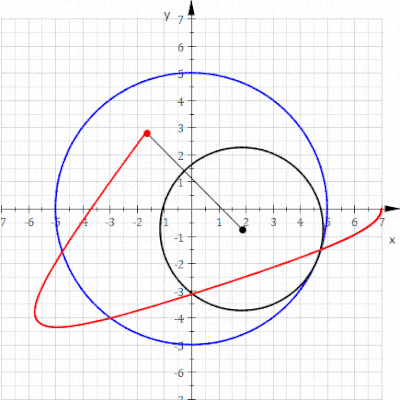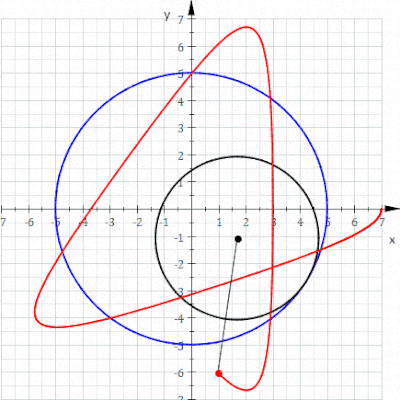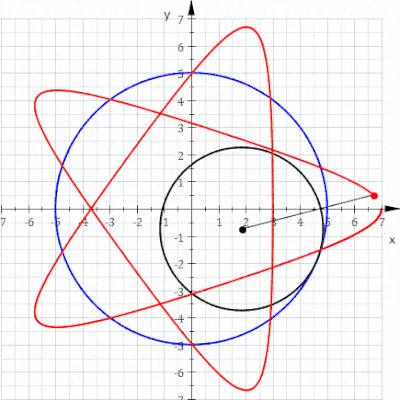
В геометрии гипотрохоид , — это рулетка очерченная точкой, прикрепленной к кругу радиуса катящемуся r, по внутренней части фиксированного круга радиуса R , где точка находится на расстоянии d от центра внутреннего круга.

Параметрические уравнения гипотрохоиды:

${\begin{aligned}&x(\theta )=(R-r)\cos \theta +d\cos \left({R-r \over r}\theta \right)\\&y(\theta )=(R-r)\sin \theta -d\sin \left({R-r \over r}\theta \right)\end{aligned}}$

где θ — угол, образованный горизонталью и центром катящегося круга (это не полярные уравнения, поскольку θ не является полярным углом). При измерении в радианах θ принимает значения от 0 до $2\pi \times {\tfrac {\operatorname {LCM} (r,R)}{R}}$ (где НОК — наименьшее общее кратное ).

Особые случаи включают гипоциклоиду с d = r и эллипс с R = 2 r и d ≠ r . Эксцентриситет эллипса

$e={\frac {2{\sqrt {d/r}}}{1+(d/r)}}$

становится 1, когда $d=r$ (см. пару Туси ).

Эллипс ) (нарисованный красным) может быть выражен как частный случай гипотрохоида с R = 2 r ( пара Туси ; здесь R = 10, r = 5, d = 1 .

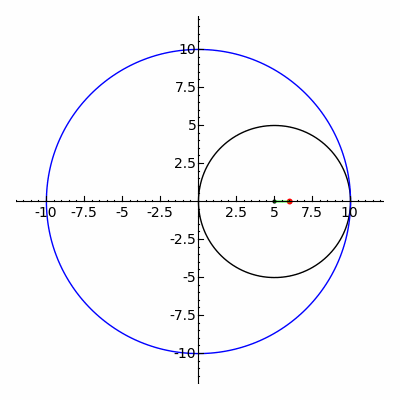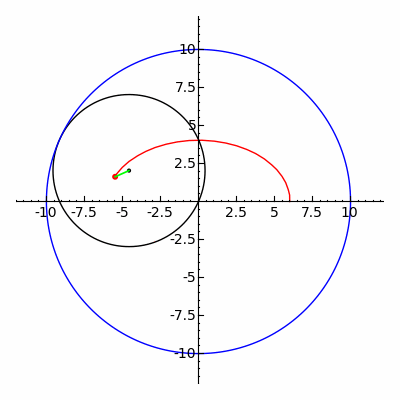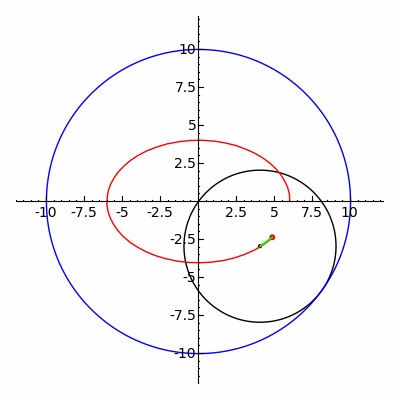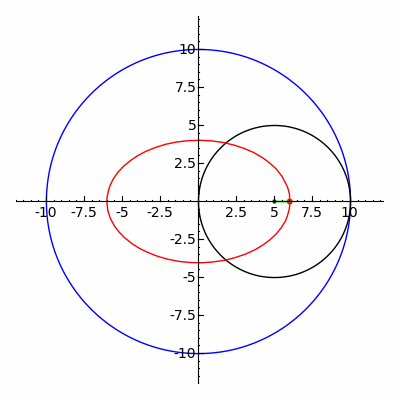
Классическая игрушка Спирограф отслеживает кривые гипотрохоиды и эпитрохоиды .

Гипотрохоиды описывают поддержку собственных значений некоторых случайных матриц с циклическими корреляциями.

См. также

• циклоида
• Циклогон
• Эпициклоида
• Розетта (орбита)
• Апсидальная прецессия
• Спирограф

Внешние ссылки

• Вайсштейн, Эрик В. «Гипотрохоид» . Математический мир .
• Флеш-анимация гипоциклоиды
• Гипотрохоид из Визуального словаря специальных плоских кривых, Кса Ли
• Интерактивная гипотрохоидная анимация
• О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Гипотрохоид» , Архив истории математики MacTutor , Университет Сент-Эндрюс