Эпитрохоид

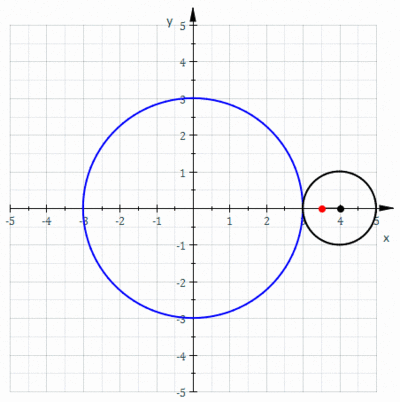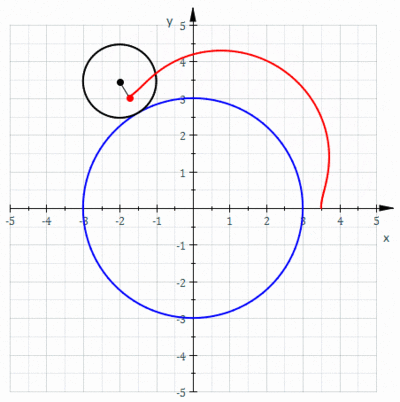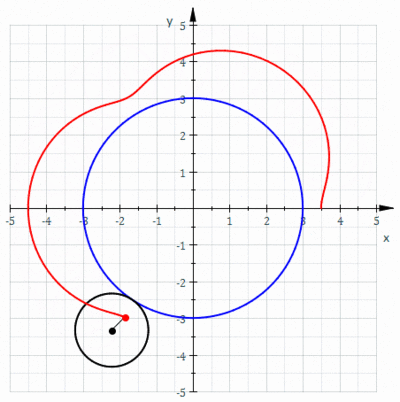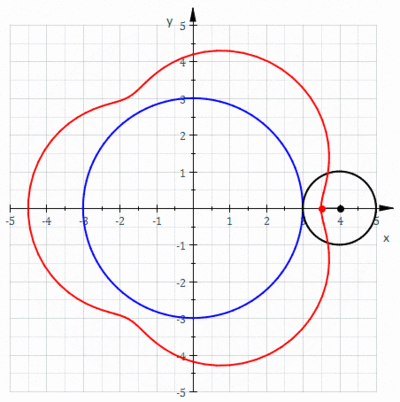
В геометрии эпитрохоид очерченная ( / ɛ p ɪ ˈ t r ɒ k ɔɪ d / или / ɛ p ɪ ˈ t r oʊ k ɔɪ d / ) — это рулетка, точкой, прикрепленной к кругу радиуса катящемуся $r,$ вокруг внешней стороны. фиксированного круга радиуса $R$ , где точка находится на расстоянии $d$ от центра внешнего круга.

Параметрические уравнения эпитрохоиды:

{\begin{aligned}&x(\theta )=(R+r)\cos \theta -d\cos \left({R+r \over r}\theta \right)\\&y(\theta )=(R+r)\sin \theta -d\sin \left({R+r \over r}\theta \right)\end{aligned}}

Параметр $θ$ геометрически представляет собой полярный угол центра внешнего круга. (Однако $θ$ не является полярным углом точки $(x(\theta ),y(\theta ))$ на эпитрохоиде.)

Особые случаи включают лимасон с $R = r$ и эпициклоиду с $d = r$ .

Классическая игрушка Спирограф рисует кривые эпитрохоиды и гипотрохоиды .

Пути планет в некогда популярной геоцентрической системе деферентов и эпициклов представляют собой эпитрохоиды с $d>r,$ как для внешних, так и для внутренних планет.

Орбита Луны, когда она центрирована вокруг Солнца, приближается к эпитрохоиде.

Камера сгорания двигателя Ванкеля представляет собой эпитрохоиду.

См. также

Ссылки

Дж. Деннис Лоуренс (1972). Каталог специальных плоских кривых . Дуврские публикации. стр. 160–164 . ISBN 0-486-60288-5 .

Внешние ссылки