Спирограф

Спирограф

Набор спирографа (британская версия начала 1980-х годов)
Изобретатель(и)	Денис Фишер
Компания	Хасбро
Страна	Великобритания
Доступность	1965 – настоящее время
Материалы	Пластик
Официальный сайт

Спирограф — это устройство для геометрического рисования, которое создает математические кривые рулетки , технически известные как гипотрохоиды и эпитрохоиды . Известная игрушечная версия была разработана британским инженером Денисом Фишером и впервые продана в 1965 году.

Это имя является зарегистрированным товарным знаком Hasbro . Inc. с 1998 года после покупки компании, которая приобрела компанию Дениса Фишера Бренд Spirograph был перезапущен по всему миру в 2013 году компанией Kahootz Toys с оригинальными конфигурациями продуктов .

История

Рисование узоров с помощью кольца и колеса спирографа.

Уличный торговец в Форт-Кочи, Индия, демонстрирует спирографы, которые он продает.

В 1827 году английский архитектор и инженер греческого происхождения Питер Юбер Девинь разработал и рекламировал «Спейраграф», устройство для создания сложных спиральных рисунков. Человек по имени Дж. Джоплинг вскоре заявил, что ранее изобрел подобные методы. Работая в Вене между 1845 и 1848 годами, Девинь сконструировал версию машины, которая помогла бы предотвратить подделку банкнот. поскольку любой из почти бесконечных вариантов моделей рулетки, которые он мог создать, было чрезвычайно сложно перепроектировать. Математик Бруно Абаканович изобрел новый спирограф между 1881 и 1900 годами. Он использовался для расчета площади, ограниченной кривыми.

Игрушки для рисования на основе шестеренок существуют как минимум с 1908 года, когда The Marvelous Wondergraph рекламировалась в каталоге Sears . Статья, описывающая, как сделать чертежную машину Wondergraph, появилась в издании Boys Mechanic в 1913 году.

Настоящая игрушка-спирограф была разработана британским инженером Денисом Фишером в период с 1962 по 1964 год путем создания машин для рисования из деталей конструктора . Фишер выставил свой спирограф на Нюрнбергской международной ярмарке игрушек 1965 года . Впоследствии он был произведен его компанией. Права на распространение в США были приобретены компанией Kenner , Inc., которая представила ее на рынке США в 1966 году и продвигала ее как креативную детскую игрушку. Позже Кеннер представил Spirotot, Magnetic Spirograph, Spiroman и различные сменные наборы.

В 2013 году компания Kahootz Toys перезапустила бренд Spirograph по всему миру с оригинальными шестернями и колесами. В современных изделиях вместо штифтов используется съемная замазка, удерживающая неподвижные детали на месте. Спирограф стал «Игрушкой года» в 1967 году и финалистом «Игрушки года» в двух категориях в 2014 году. Kahootz Toys была приобретена компанией PlayMonster LLC в 2019 году.

Операция

Оригинальный спирограф, выпущенный в США, состоял из двух пластиковых колец (или статоров ) разного размера с зубьями шестерни как на внутренней, так и на внешней стороне окружности. После того, как любое из этих колец удерживалось на месте (с помощью штифтов, клея или вручную), любое из нескольких предоставленных зубчатых колес (или роторов ), каждое из которых имело отверстия для шариковой ручки , можно было вращать вокруг кольца, чтобы рисовать геометрические фигуры. . Позже в суперспирографе появились дополнительные формы, такие как кольца, треугольники и прямые полосы. Все края каждой детали имеют зубцы для зацепления с любой другой деталью; Шестерни меньшего размера помещаются внутри колец большего размера, но они также могут вращаться вдоль внешнего края колец или даже вокруг друг друга. Шестерни можно комбинировать по-разному. В наборы часто входили ручки разного цвета, которые могли улучшить дизайн за счет переключения цветов, как показано на примерах, показанных здесь.

Новички часто проскальзывают шестерни, особенно при использовании отверстий по краям больших колес, что приводит к ломаным или неправильным линиям. Опытные пользователи могут научиться перемещать несколько фигур относительно друг друга (скажем, треугольник вокруг кольца, с кругом, «перелезающим» из кольца на треугольник).

• 
  Анимация спирографа
• 
  Несколько рисунков спирографа, нарисованных с помощью набора спирографов с использованием нескольких ручек разного цвета.
• 
  Крупный план колеса спирографа

Математическая основа

Геометрические конструкции для математического объяснения спирографа.

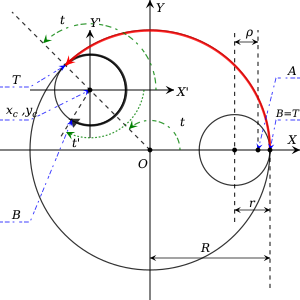
Рассмотрим фиксированный внешний круг $C_{o}$ радиуса $R$ сосредоточено в начале координат. Меньший внутренний круг $C_{i}$ радиуса $r<R$ катится внутри $C_{o}$ и непрерывно касается его. $C_{i}$ предполагается, что он никогда не поскользнется $C_{o}$ (в настоящем спирографе такое проскальзывание предотвращают зубцы на обоих кругах). Теперь предположим, что точка $A$ лежит где-то внутри $C_{i}$ находится на расстоянии $\rho <r$ от $C_{i}$центр. Этот момент $A$ соответствует отверстию для ручки во внутреннем диске настоящего спирографа. Без ограничения общности можно считать, что в начальный момент точка $A$ был на $X$ ось. Чтобы найти траекторию, созданную спирографом, следуйте пункту $A$ как внутренний круг приходит в движение.

Теперь отметьте две точки $T$ на $C_{o}$ и $B$ на $C_{i}$. Суть $T$ всегда указывает место соприкосновения двух окружностей. Точка $B$, однако, будет путешествовать дальше $C_{i}$, а его начальное положение совпадает с $T$. После установки $C_{i}$ в движении против часовой стрелки вокруг $C_{o}$, $C_{i}$ имеет вращение по часовой стрелке относительно своего центра. Расстояние, в котором находится эта точка $B$ проходит по $C_{i}$ такое же, как и точка, через которую проходит точка касания $T$ на $C_{o}$, из-за отсутствия скольжения.

Теперь определим новую (относительную) систему координат. $(X',Y')$ с его происхождением в центре $C_{i}$ и его оси параллельны $X$ и $Y$. Пусть параметр $t$ - угол, под которым точка касания $T$ вращается $C_{o}$, и $t'$ быть углом, под которым $C_{i}$ вращается (т.е. посредством чего $B$ путешествия) в относительной системе координат. Поскольку скольжения нет, расстояние, пройденное $B$ и $T$ вдоль соответствующих окружностей должны быть одинаковыми, поэтому

$tR=(t-t')r,$

или эквивалентно,

$t'=-{\frac {R-r}{r}}t.$

Принято считать, что движение против часовой стрелки соответствует положительному изменению угла, а движение по часовой стрелке — отрицательному изменению угла. Знак минус в приведенной выше формуле ( $t'<0$) соответствует этому соглашению.

Позволять $(x_{c},y_{c})$ быть координатами центра $C_{i}$ в абсолютной системе координат. Затем $R-r$ представляет собой радиус траектории центра $C_{i}$, который (опять же в абсолютной системе) совершает круговое движение, таким образом:

${\begin{aligned}x_{c}&=(R-r)\cos t,\\y_{c}&=(R-r)\sin t.\end{aligned}}$

Как определено выше, $t'$ – угол поворота в новой относительной системе. Потому что точка $A$ подчиняется обычному закону кругового движения, его координаты в новой относительной системе координат $(x',y')$ являются

${\begin{aligned}x'&=\rho \cos t',\\y'&=\rho \sin t'.\end{aligned}}$

Чтобы получить траекторию $A$ в абсолютной (старой) системе координат сложите эти два движения:

${\begin{aligned}x&=x_{c}+x'=(R-r)\cos t+\rho \cos t',\\y&=y_{c}+y'=(R-r)\sin t+\rho \sin t',\\\end{aligned}}$

где $\rho$ определено выше.

Теперь используйте соотношение между $t$ и $t'$ как получено выше, чтобы получить уравнения, описывающие траекторию точки $A$ по одному параметру $t$:

${\begin{aligned}x&=x_{c}+x'=(R-r)\cos t+\rho \cos {\frac {R-r}{r}}t,\\y&=y_{c}+y'=(R-r)\sin t-\rho \sin {\frac {R-r}{r}}t\\\end{aligned}}$

(используя тот факт, что функция $\sin$ это странно ).

Удобно представить приведенное выше уравнение через радиус $R$ из $C_{o}$ и безразмерныйпараметры, описывающие структуру спирографа. А именно, пусть

$l={\frac {\rho }{r}}$

и

$k={\frac {r}{R}}.$

Параметр $0\leq l\leq 1$ показывает, насколько далеко находится точка $A$ находится от центра г. $C_{i}$. В то же время, $0\leq k\leq 1$ показывает, насколько велик внутренний круг $C_{i}$ это по отношению к внешнему $C_{o}$.

Сейчас наблюдается, что

${\frac {\rho }{R}}=lk,$

и поэтому уравнения траектории принимают вид

${\begin{aligned}x(t)&=R\left[(1-k)\cos t+lk\cos {\frac {1-k}{k}}t\right],\\y(t)&=R\left[(1-k)\sin t-lk\sin {\frac {1-k}{k}}t\right].\\\end{aligned}}$

Параметр $R$ является параметром масштабирования и не влияет на структуру спирографа. Различные значения $R$ дадут аналогичные рисунки спирографа.

Два крайних случая $k=0$ и $k=1$ приводят к вырожденным траекториям спирографа. В первом крайнем случае, когда $k=0$, у нас есть простой круг радиуса $R$, что соответствует случаю, когда $C_{i}$ сократилось до точки. (Деление на $k=0$ в формуле не является проблемой, поскольку оба $\sin$ и $\cos$ являются ограниченными функциями.)

Другой крайний случай $k=1$ соответствует внутреннему кругу $C_{i}$радиус $r$ соответствие радиусу $R$ внешнего круга $C_{o}$, то есть $r=R$. В этом случае траектория представляет собой одну точку. Интуитивно, $C_{i}$ слишком велик, чтобы его можно было катить внутри такого же размера $C_{o}$ без скольжения.

Если $l=1$, тогда точка $A$ находится на окружности $C_{i}$. В этом случае траектории называются гипоциклоидами , и приведенные выше уравнения сводятся к уравнениям для гипоциклоиды.

См. также

• Кардиоида
• Апсидальная прецессия
• Циклограф
• Геометрический токарный станок
• Гильош
• Гармонограф
• Гипотрохоид
• Кривая Лиссажу
• Список периодических функций
• Пантограф
• Шестерня
• Роза (математика)
• Розетта (орбита)
• Туманность Спирограф — планетарная туманность с тонкой филигранью, напоминающей спирограф.
• Напиши пару

Внешние ссылки

• Официальный сайт
• Воевудко А.Е. (12 марта 2018 г.). «Географические кривые» . Код проекта .