Перпендикуляр

В геометрии два геометрических объекта являются перпендикулярными , если их пересечение образует прямые углы ( углы шириной 90 градусов или π/2 радиана) в точке пересечения, называемой футом . Условие перпендикулярности можно представить графически с помощью символа перпендикуляра , ⟂. Перпендикулярные пересечения могут происходить между двумя прямыми (или двумя отрезками), между прямой и плоскостью, а также между двумя плоскостями.

Перпендикулярность — это один из частных случаев более общей математической концепции ортогональности ; Перпендикулярность — это ортогональность классических геометрических объектов. Таким образом, в высшей математике слово «перпендикуляр» иногда используется для описания гораздо более сложных геометрических условий ортогональности, например, между поверхностью и ее вектором нормали .

Говорят, что прямая перпендикулярна другой прямой, если две прямые пересекаются под прямым углом. ^[2]Явно первая линия перпендикулярна второй линии, если (1) две линии пересекаются; и (2) в точке пересечения прямой угол на одной стороне первой линии разрезается второй линией на два равных угла . Можно показать, что перпендикулярность симметрична , то есть если первая линия перпендикулярна второй линии, то вторая линия также перпендикулярна первой. По этой причине мы можем говорить о двух линиях как о перпендикулярных (друг другу) без указания порядка. Отличный пример перпендикулярности можно увидеть в любом компасе, обратите внимание на стороны света; Север, Восток, Юг, Запад (NESW) Линия NS перпендикулярна линии WE, а углы NE, ES, SW и WN составляют 90° друг к другу.

Перпендикулярность легко распространяется на отрезки и лучи . Например, отрезок прямой ${\overline {AB}}$ перпендикулярен отрезку прямой ${\overline {CD}}$ если, когда каждая из них продлена в обоих направлениях, образуя бесконечную линию, эти две полученные линии перпендикулярны в указанном выше смысле. В символах, ${\overline {AB}}\perp {\overline {CD}}$ означает, что отрезок AB перпендикулярен отрезку CD. ^[3]

Прямая называется перпендикулярной плоскости, если она перпендикулярна каждой прямой в плоскости, которую она пересекает. Это определение зависит от определения перпендикулярности между линиями.

Две плоскости в пространстве называются перпендикулярными, если двугранный угол , под которым они встречаются, является прямым.

Основание перпендикуляра [ править ]

Слово « фут» часто используется в отношении перпендикуляров. Пример такого использования показан на верхней диаграмме выше и в ее заголовке. Диаграмма может иметь любую ориентацию. Стопа не обязательно находится внизу.

Точнее, пусть $A$ — точка, а $m$ — линия. Если $B$ — точка пересечения $m$ и единственной прямой, проходящей через $и$ перпендикулярной $m$ , то $B$ называется основанием этого перпендикуляра, проходящего через $A.$ A

Построение перпендикуляра [ править ]

Построение перпендикуляра (синего цвета) к прямой АВ через точку Р.

Построение перпендикуляра к полупрямой h из точки Р (применимо не только в конечной точке А, М выбирается свободно), анимация в конце с паузой 10 с

Чтобы провести перпендикуляр к прямой АВ через точку Р с помощью построения циркуля и линейки , поступите следующим образом (см. рисунок слева):

Шаг 1 (красный): постройте круг с центром в точке P, чтобы создать точки A' и B' на линии AB, которые равноудалены от P.
Шаг 2 (зеленый): постройте круги с центрами A' и B', имеющие одинаковый радиус. Пусть Q и P — точки пересечения этих двух окружностей.
Шаг 3 (синий): соедините Q и P, чтобы построить нужный перпендикуляр PQ.

Чтобы доказать, что PQ перпендикулярен AB, используйте теорему о сравнении SSS для QPA' и QPB', чтобы заключить, что углы OPA' и OPB' равны. Затем используйте теорему сравнения SAS для треугольников OPA' и OPB', чтобы заключить, что углы POA и POB равны.

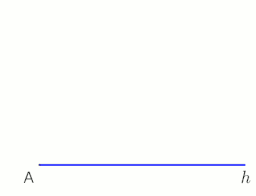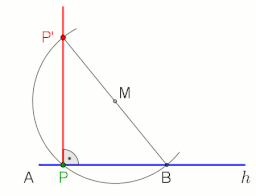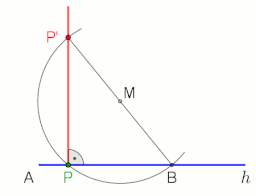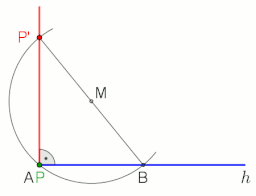
Чтобы провести перпендикуляр к линии g в точке P или через нее, используя теорему Фалеса , см. анимацию справа.

Теорема Пифагора может быть положена в основу методов построения прямых углов. Например, подсчитав звенья, можно получить три куска цепи с соотношением длин 3:4:5. Их можно сложить в виде треугольника, у которого против самой длинной стороны будет прямой угол. Этот метод полезен при планировке садов и полей, где размеры большие и большая точность не нужна. Цепи можно использовать повторно, когда это необходимо.

По отношению к параллельным линиям [ править ]

Если две линии ( a и b ) перпендикулярны третьей линии ( c ), все углы, образованные вдоль третьей линии, являются прямыми. Следовательно, в евклидовой геометрии любые две прямые, перпендикулярные третьей прямой , параллельны друг другу из-за постулата параллельности . И наоборот, если одна линия перпендикулярна второй линии, она также перпендикулярна любой линии, параллельной этой второй линии.

На рисунке справа все углы, заштрихованные оранжевым цветом, конгруэнтны друг другу, а все углы, заштрихованные зеленым, конгруэнтны друг другу, поскольку вертикальные углы конгруэнтны, а чередующиеся внутренние углы, образованные поперечными разрезающими параллельными линиями, равны друг другу. конгруэнтный. Следовательно, если прямые a и b параллельны, любой из следующих выводов приводит ко всем остальным:

Один из углов на диаграмме — прямой.
Один из углов, заштрихованных оранжевым цветом, равен одному из углов, заштрихованных зеленым.
Линия с перпендикулярна линии а .
Линия c перпендикулярна линии b .
Все четыре угла равны.

В вычислениях расстояний [ править ]

В геометрии расстояние по перпендикуляру между двумя объектами — это расстояние от одного до другого, измеренное вдоль линии , перпендикулярной одному или обоим объектам.

Расстояние от точки до линии — это расстояние до ближайшей точки на этой линии. Это точка, в которой отрезок от нее до данной точки перпендикулярен прямой.

Аналогично, расстояние от точки до кривой измеряется отрезком линии, перпендикулярным касательной к кривой в ближайшей точке кривой.

Расстояние от точки до плоскости измеряется как длина от точки по отрезку, перпендикулярному плоскости, то есть перпендикулярному всем прямым в плоскости, проходящим через ближайшую к данной точке точку плоскости. .

Другие случаи включают в себя:

Точка на плоскости, ближайшая к началу координат , для перпендикулярного расстояния от начала координат до плоскости в трехмерном пространстве.
Ближайшее расстояние между наклонными линиями для перпендикулярного расстояния между двумя непараллельными линиями в трехмерном пространстве.

Перпендикулярная регрессия подгоняет линию к точкам данных путем минимизации суммы квадратов перпендикулярных расстояний от точек данных до линии. Существуют и другие методы подбора геометрической кривой, использующие перпендикулярное расстояние для измерения качества подбора, например, метод общих наименьших квадратов .

Понятие перпендикулярного расстояния можно обобщить до

ортогональное расстояние между более абстрактными негеометрическими ортогональными объектами, как в линейной алгебре (например, анализ главных компонент );
расстояние по нормали, включающее нормаль к поверхности , между произвольной точкой и ее основанием на поверхности. Его можно использовать для подгонки поверхностей и для определения смещенных поверхностей .

График функций [ править ]

В двумерной плоскости прямые углы могут быть образованы двумя пересекающимися прямыми, если произведение их наклонов равно −1. Таким образом, для двух линейных функций $y_{1}(x)=m_{1}x+b_{1}$ и $y_{2}(x)=m_{2}x+b_{2}$ , графики функций будут перпендикулярны, если $m_{1}m_{2}=-1.$

Скалярное произведение векторов так , также можно использовать для получения того же результата: сначала сдвиньте координаты чтобы начало координат располагалось там, где пересекаются линии. Затем определите два смещения вдоль каждой линии, ${\vec {r}}_{j}$ , для $(j=1,2).$ Теперь воспользуемся тем фактом, что скалярное произведение равно нулю для перпендикулярных векторов:

{\vec {r}}_{1}=x_{1}{\hat {x}}+y_{1}{\hat {y}}=x_{1}{\hat {x}}+m_{1}x_{1}{\hat {y}}

{\vec {r}}_{2}=x_{2}{\hat {x}}+y_{2}{\hat {y}}=x_{2}{\hat {x}}+m_{2}x_{2}{\hat {y}}

{\vec {r}}_{1}\cdot {\vec {r}}_{2}=\left(1+m_{1}m_{2}\right)x_{1}x_{2}=0

\therefore m_{1}m_{2}=-1

(пока не

x_{1}

или

x_{2}

исчезает.)

Оба доказательства справедливы для горизонтальных и вертикальных линий в той степени, в которой мы можем предположить, что один наклон равен $\varepsilon$ , и возьмем предел, который $\varepsilon \rightarrow 0.$ Если один наклон стремится к нулю, другой стремится к бесконечности.

В кругах и других кониках [ править ]

Круги [ править ]

Каждый диаметр круга этому кругу в точке , перпендикулярен касательной к где диаметр пересекает круг.

Отрезок, проходящий через центр окружности и делящий хорду пополам , перпендикулярен хорде.

Если пересечение любых двух перпендикулярных хорд делит одну хорду на длины a и b , а другую хорду на длины c и d , то a ² + б ² + с ² + д ² равен квадрату диаметра. ^[4]

Сумма квадратов длин любых двух перпендикулярных хорд, пересекающихся в данной точке, равна квадрату длин любых других двух перпендикулярных хорд, пересекающихся в той же точке, и определяется выражением 8 r. ² – 4 р. ² (где r — радиус круга, а p — расстояние от центральной точки до точки пересечения). ^[5]

Теорема Фалеса утверждает, что две прямые, проходящие через одну и ту же точку окружности, но проходящие через противоположные конечные точки диаметра, перпендикулярны. Это эквивалентно утверждению, что любой диаметр окружности образует прямой угол в любой точке окружности, кроме двух конечных точек диаметра.

Эллипсы [ править ]

Большая и малая оси эллипса . перпендикулярны друг другу и касательным к эллипсу в точках пересечения осей эллипса

Большая ось эллипса перпендикулярна директрисе и каждой широкой прямой кишке .

Parabolas[editпритчи

В параболе ось симметрии перпендикулярна широкой прямой кишке, директрисе и касательной в точке, где ось пересекает параболу.

От точки касательной к вершине параболы другая касательная к параболе перпендикулярна линии, проходящей через фокус параболы .

Ортоптическое свойство параболы состоит в том, что если две касательные к параболе перпендикулярны друг другу, то они пересекаются по направляющей. И наоборот, две касательные, пересекающиеся по направляющей, перпендикулярны. Это означает, что любая парабола, если смотреть из любой точки ее директрисы, образует прямой угол.

Гиперболы [ править ]

Поперечная ось гиперболы . перпендикулярна сопряженной оси и каждой направляющей

Произведение перпендикулярных расстояний от точки P на гиперболе или на сопряженной ей гиперболе до асимптот является константой, не зависящей от местоположения P.

Прямоугольная гипербола имеет асимптоты , перпендикулярные друг другу. Он имеет эксцентриситет , равный ${\sqrt {2}}.$

В полигонах [ править ]

Треугольники [ править ]

Катеты прямоугольного треугольника перпендикулярны друг другу.

Высоты треугольника основаниям соответствующим . перпендикулярны Серединные перпендикуляры сторон также играют важную роль в геометрии треугольника.

равнобедренного Линия Эйлера треугольника перпендикулярна основанию треугольника.

Теорема Дроза -Фарни о прямой треугольника касается свойства двух перпендикулярных прямых, пересекающихся в ортоцентре .

Теорема Харкорта касается соотношения отрезков прямых, проходящих через вершину и перпендикулярных к любой прямой, касательной треугольника к вписанной окружности .

Четырехугольники [ править ]

В квадрате или другом прямоугольнике все пары смежных сторон перпендикулярны. Правильная трапеция — это трапеция , у которой две пары смежных сторон перпендикулярны.

Каждая из четырех сторон четырехугольника середину является перпендикуляром к стороне, проходящим через противоположной стороны.

Ортодиагональный четырехугольник – это четырехугольник, диагонали которого перпендикулярны. К ним относятся квадрат , ромб и воздушный змей . По теореме Брахмагупты в ортодиагональном четырехугольнике, который также является вписанным , линия, проходящая через середину одной стороны и точку пересечения диагоналей, перпендикулярна противоположной стороне.

По теореме Ван Обеля , если на сторонах четырехугольника снаружи построены квадраты, отрезки, соединяющие центры противоположных квадратов, перпендикулярны и равны по длине.

Линии в трех измерениях [ править ]

До трех линий в трехмерном пространстве могут быть попарно перпендикулярными, примером чему служат оси x, y и z трехмерной декартовой системы координат .

См. также [ править ]

Примечания [ править ]

^ Кей (1969 , стр. 114)
^ Кей (1969 , стр. 91)
^ Кей (1969 , стр. 91)
^ Посаментье и Салкинд, «Сложные проблемы геометрии» , Дувр, 2-е издание, 1996: стр. 104–105, № 4–23.
^ Журнал колледжа математики 29 (4), сентябрь 1998 г., стр. 331, задача 635.

Ссылки [ править ]

Альтшиллер-Корт, Натан (1952) [1-е изд. 1925], Геометрия колледжа: введение в современную геометрию треугольника и круга (2-е изд.), Нью-Йорк: Barnes & Noble.
Кей, Дэвид К. (1969), Геометрия колледжа , Нью-Йорк: Холт, Райнхарт и Уинстон , LCCN 69-12075

Внешние ссылки [ править ]

Определение: перпендикулярно с интерактивной анимацией.
Как нарисовать серединный перпендикуляр к линии с помощью циркуля и линейки (анимационная демонстрация).
Как провести перпендикуляр в конечной точке луча с помощью циркуля и линейки (анимационная демонстрация).

[1] Кей (1969 , стр. 114)

[2] Кей (1969 , стр. 91)

[3] Кей (1969 , стр. 91)

[4] Посаментье и Салкинд, «Сложные проблемы геометрии» , Дувр, 2-е издание, 1996: стр. 104–105, № 4–23.

[5] Журнал колледжа математики 29 (4), сентябрь 1998 г., стр. 331, задача 635.

[1]

[2]

[3]

[4]

[5]