Платоново твердое тело

В геометрии Платоново тело — это выпуклый правильный многогранник в трёхмерном евклидовом пространстве . Правильный многогранник означает, что грани представляют собой конгруэнтные (одинаковые по форме и размеру) правильные многоугольники (все углы равны и все ребра сходится одинаковое количество граней конгруэнтны), и в каждой вершине . Таких многогранников всего пять:

Тетраэдр	Куб	Октаэдр	Додекаэдр	Икосаэдр
Четыре лица	Шесть лиц	Восемь лиц	Двенадцать лиц	Двадцать лиц
( Animation , 3D model )	( Animation , 3D model )	( Animation , 3D model )	( Animation , 3D model )	( Animation , 3D model )

Геометры изучали Платоновы тела на протяжении тысячелетий. Они названы в честь древнегреческого философа Платона , который в одном из своих диалогов « Тимей» выдвинул гипотезу , что классические элементы состоят из этих правильных твердых тел.

История

Кеплера Платоническая твердотельная модель Солнечной системы из Mysterium Cosmographicum (1596 г.)

Отнесение к элементам в «Harmonices Mundi» Кеплера.

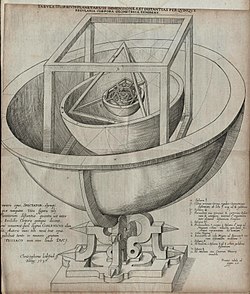
Платоновы тела известны с античных времен. Было высказано предположение, что определенные резные каменные шары, созданные жителями неолита Шотландии позднего эти формы представляют собой ; однако эти шары имеют закругленные выступы, а не многогранники, число выступов часто отличалось от числа вершин платоновых тел, не существует шара, выступы которого соответствовали бы 20 вершинам додекаэдра, и расположение выступов не было всегда симметричен.

Древние греки широко изучали Платоновы тела. Некоторые источники (например, Прокл ) приписывают Пифагору свое открытие . Другие данные свидетельствуют о том, что он, возможно, был знаком только с тетраэдром, кубом и додекаэдром и что открытие октаэдра и икосаэдра принадлежит Теэтету , современнику Платона. В любом случае Теэтет дал математическое описание всех пяти и, возможно, был ответственным за первое известное доказательство того, что других выпуклых правильных многогранников не существует.

Платоновые тела занимают видное место в философии Платона , их тезки. Платон писал о них в диалоге «Тимей» ок. 360 г. до н.э., в котором он связал каждый из четырех классических элементов ( землю , воздух , воду и огонь ) с правильным твердым телом. Земля ассоциировалась с кубом, воздух — с октаэдром, вода — с икосаэдром, а огонь — с тетраэдром.

О пятом платоновском теле, додекаэдре, Платон неясно заметил: «...бог использовал [его] для расположения созвездий на всем небе». Аристотель добавил пятый элемент, аитер (эфир по-латыни, «эфир» по-английски) и постулировал, что небеса состоят из этого элемента, но он не был заинтересован в сопоставлении его с пятым телом Платона.

Евклид полностью математически описал Платоновы тела в « Началах» , последняя книга (книга XIII) которых посвящена их свойствам. Предложения 13–17 в книге XIII описывают построение тетраэдра, октаэдра, куба, икосаэдра и додекаэдра в указанном порядке. Для каждого твердого тела Евклид находит отношение диаметра описанной сферы к длине ребра. В предложении 18 он утверждает, что больше не существует выпуклых правильных многогранников. Андреас Спейзер отстаивал точку зрения, согласно которой построение пяти правильных тел является главной целью дедуктивной системы, канонизированной в « Элементах» . Большая часть информации в Книге XIII, вероятно, заимствована из работ Теэтета.

В 16 веке немецкий астроном Иоганн Кеплер попытался связать пять известных в то время внеземных планет с пятью Платоновыми телами. В книге «Mysterium Cosmographicum» , опубликованной в 1596 году, Кеплер предложил модель Солнечной системы , в которой пять твердых тел помещены друг в друга и разделены серией вписанных и описанных сфер. Кеплер предположил, что отношения расстояний между шестью планетами, известными в то время, можно было понять с точки зрения пяти платоновых тел, заключенных в сферу, которая представляла орбиту Сатурна . Каждая из шести сфер соответствовала одной из планет ( Меркурию , Венере , Земле , Марсу , Юпитеру и Сатурну). Твердые тела были упорядочены так, что самым внутренним был октаэдр, за ним следовали икосаэдр, додекаэдр, тетраэдр и, наконец, куб, тем самым диктуя структуру Солнечной системы и отношения расстояний между планетами с помощью платоновых тел. В конце концов от первоначальной идеи Кеплера пришлось отказаться, но в результате его исследований родилась его идея. три закона орбитальной динамики , первый из которых заключался в том, что орбиты планет представляют собой эллипсы, а не круги, изменив ход физики и астрономии. Он также открыл тела Кеплера , представляющие собой два невыпуклых правильных многогранника.

Декартовы координаты

Для платоновых тел с центром в начале координат простые декартовы координаты вершин приведены ниже. Греческая буква φ используется для обозначения золотого сечения. 1 + √ 5 / 2 ≈ 1.6180.

Параметры

Фигура	Тетраэдр		Октаэдр	Куб	Икосаэдр		Додекаэдр
Лица	4		8	6	20		12
Вершины	4		6 (2 × 3)	8	12 (4 × 3)		20 (8 + 4 × 3)
Позиция	1	2			1	2	1	2
Вертекс координаты	(1, 1, 1) (1, −1, −1) (−1, 1, −1) (−1, −1,  1)	(−1, −1, −1) (−1, 1, 1) (  1, −1,  1) (  1,  1, −1)	(±1,  0,  0) (  0, ±1,  0) (  0,  0, ±1)	(±1, ±1, ±1)	(  0, ±1, ± φ ) (±1, ± φ ,  0) (± φ ,  0, ±1)	(  0, ± φ , ±1) (± φ , ±1,  0) (±1,  0, ± φ )	(±1, ±1, ±1) (  0, ± 1 / φ , ± φ ) (± 1 / φ , ± φ ,   0) (± φ ,  0, ± 1 / ж )	(±1, ±1, ±1) (  0, ± φ , ± 1 / ж ) (± φ , ± 1 / ф ,   0) (± 1 / φ ,   0, ± φ )

Координаты тетраэдра, додекаэдра и икосаэдра заданы в двух положениях так, что каждая может быть выведена из другой: в случае тетраэдра - путем изменения всех координат знака ( центральная симметрия ) или, в остальных случаях, путем обмена двумя координатами ( отражение относительно любой из трех диагональных плоскостей).

Эти координаты раскрывают определенные отношения между платоновыми телами: вершины тетраэдра представляют половину вершин куба, как {4,3} или , один из двух наборов из 4 вершин в двойных положениях, например h{4,3} или . Обе позиции тетраэдра образуют составной звездчатый октаэдр .

Координаты икосаэдра связаны с двумя чередующимися наборами координат неоднородного усеченного октаэдра t{3,4} или , также называемый курносым октаэдром , как s{3,4} или , и виден в соединении двух икосаэдров .

Восемь вершин додекаэдра являются общими с кубом. Выполнение всех ориентаций приводит к соединению пяти кубов .

Комбинаторные свойства

Выпуклый многогранник является платоновым телом тогда и только тогда, когда выполняются все три следующих требования.

• Все его грани представляют собой конгруэнтные выпуклые правильные многоугольники .
• Ни одна из его граней не пересекается, кроме как по краям.
• сходится одинаковое количество граней В каждой его вершине .

Таким образом, каждому Платонову телу можно присвоить пару { p , q целых чисел }, где p — количество ребер (или, что то же самое, вершин) каждой грани, а q — количество граней (или, что то же самое, ребер), которые встречаются в каждой вершине. Эта пара { p , q }, называемая символом Шлефли , дает комбинаторное описание многогранника. Символы Шлефли пяти Платоновых тел приведены в таблице ниже.

Свойства платоновых тел

Многогранник		Вершины	Края	Лица	Символ Шлефли	Конфигурация вершин
тетраэдр		4	6	4	{3, 3}	3.3.3
куб		8	12	6	{4, 3}	4.4.4
октаэдр		6	12	8	{3, 4}	3.3.3.3
додекаэдр		20	30	12	{5, 3}	5.5.5
икосаэдр		12	30	20	{3, 5}	3.3.3.3.3

Вся остальная комбинаторная информация об этих телах, такая как общее количество вершин ( V ), ребер ( E ) и граней ( F ), может быть определена из p и q . Поскольку любое ребро соединяет две вершины и имеет две смежные грани, мы должны иметь:

$$pF=2E=qV.\,$$

Другая связь между этими значениями определяется формулой Эйлера :

$$V-E+F=2.\,$$

Это можно доказать многими способами. Вместе эти три отношения полностью определяют V , E и F :

$$V={\frac {4p}{4-(p-2)(q-2)}},\quad E={\frac {2pq}{4-(p-2)(q-2)}},\quad F={\frac {4q}{4-(p-2)(q-2)}}.$$

Замена p и q меняет местами F и V, оставляя E неизменным. Геометрическую интерпретацию этого свойства см. в § Двойственные многогранники .

В качестве конфигурации

Элементы многогранника можно выразить в виде матрицы конфигурации . Строки и столбцы соответствуют вершинам, ребрам и граням. Диагональные числа говорят, сколько элементов каждого элемента встречается во всем многограннике. Недиагональные числа показывают, сколько элементов столбца встречается в элементе строки или рядом с ним. Матрицы конфигураций двойных пар многогранников повернуты на 180 градусов друг от друга.

{п, д}	Платонические конфигурации
Групповой заказ : g = 8 pq /(4 - ( p - 2)( q - 2))	г = 24	г = 48		г = 120
v и ж v г /2 г д д и 2 г /4 2 ж п п г /2 р	{3,3} 4 3 3 2 6 2 3 3 4	{3,4} 6 4 4 2 12 2 3 3 8	{4,3} 8 3 3 2 12 2 4 4 6	{3,5} 12 5 5 2 30 2 3 3 20	{5,3} 20 3 3 2 30 2 5 5 12

Классификация

Классический результат состоит в том, что существует только пять выпуклых правильных многогранников. Два общих аргумента, приведенных ниже, показывают, что может существовать не более пяти Платоновых тел, но положительная демонстрация существования любого данного твердого тела - это отдельный вопрос, требующий явной конструкции.

Геометрическое доказательство

Полигональные сети вокруг вершины

{3,3} Дефект 180°	{3,4} Дефект 120°	{3,5} Дефект 60°	{3,6} Дефект 0°
{4,3} Дефект 90°	{4,4} Дефект 0°	{5,3} Дефект 36°	{6,3} Дефект 0°
Для вершины необходимо как минимум 3 грани и дефект угла . Дефект угла 0° заполнит евклидову плоскость правильной мозаикой. По теореме Декарта число вершин равно 720°/ дефект .

Следующий геометрический аргумент очень похож на тот, который приводит Евклид в « Началах» :

1. Каждая вершина тела должна быть вершиной как минимум трёх граней.
2. В каждой вершине твердого тела сумма углов между смежными гранями между соответствующими смежными сторонами должна быть строго меньше 360°. Величина менее 360° называется угловым дефектом .
3. Правильные многоугольники с шестью и более сторонами имеют только углы 120° и более, поэтому общей гранью должен быть треугольник, квадрат или пятиугольник. Для этих разных форм лиц справедливо следующее:

   Треугольные лица

   Каждая вершина правильного треугольника имеет угол 60°, поэтому фигура может иметь три, четыре или пять треугольников, сходящихся в вершине; это тетраэдр, октаэдр и икосаэдр соответственно.

   Квадратные лица

   Каждая вершина квадрата равна 90°, поэтому возможно только одно расположение с тремя гранями в вершине - куб.

   Пятиугольные грани

   Каждая вершина равна 108°; опять-таки возможно только одно расположение трех граней в вершине — додекаэдр.

   В общей сложности это дает пять возможных платоновых тел.

доказательство

Чисто топологическое доказательство можно провести, используя только комбинаторную информацию о твердых телах. Ключевым моментом является наблюдение Эйлера о том, что V − E + F = 2, и тот факт, что pF = 2 E = qV , где p обозначает количество ребер каждой грани, а q — количество ребер, сходящихся в каждой вершине. Объединяя эти уравнения, получаем уравнение

Ортографические проекции и диаграммы Шлегеля с гамильтоновыми циклами вершин пяти платоновых тел - только октаэдр имеет эйлеров путь или цикл, расширяя его путь пунктиром.

$${\frac {2E}{q}}-E+{\frac {2E}{p}}=2.$$

Тогда простая алгебраическая манипуляция дает

$${1 \over q}+{1 \over p}={1 \over 2}+{1 \over E}.$$

Поскольку E строго положительно, мы должны иметь

$${\frac {1}{q}}+{\frac {1}{p}}>{\frac {1}{2}}.$$

Используя тот факт, что p и q должны быть не менее 3, можно легко увидеть, что существует только пять возможностей для { p , q }:

{3, 3}, {4, 3}, {3, 4}, {5, 3}, {3, 5}.

Геометрические свойства

Углы

С каждым платоновым телом связано несколько углов . Двугранный угол — это внутренний угол между любыми двумя плоскостями граней. Двугранный угол θ твердого тела { p , q } определяется формулой

$$\sin \left({\frac {\theta }{2}}\right)={\frac {\cos \left({\frac {\pi }{q}}\right)}{\sin \left({\frac {\pi }{p}}\right)}}.$$

Иногда это удобнее выражать через тангенс :

$$\tan \left({\frac {\theta }{2}}\right)={\frac {\cos \left({\frac {\pi }{q}}\right)}{\sin \left({\frac {\pi }{h}}\right)}}.$$

Величина h (называемая числом Кокстера ) равна 4, 6, 6, 10 и 10 для тетраэдра, куба, октаэдра, додекаэдра и икосаэдра соответственно.

в Недостаток угла вершине многогранника — это разница между суммой углов граней в этой вершине и 2 π . Дефект δ в любой вершине платоновых тел { p , q } равен

$$\delta =2\pi -q\pi \left(1-{2 \over p}\right).$$

По теореме Декарта это равно 4 π, делённому на количество вершин (т.е. общий дефект во всех вершинах равен 4 π ).

Трехмерным аналогом плоского угла является телесный угол . Телесный угол Ω в вершине платонова тела определяется через двугранный угол выражением

$$\Omega =q\theta -(q-2)\pi .\,$$

Это следует из сферического избытка формулы сферического многоугольника и того факта, что вершинная фигура многогранника { p , q } является правильным q -угольником.

Телесный угол грани, вытянутой из центра платонового тела, равен телесному углу полной сферы (4 π стерадиана), разделенному на количество граней. Это равно угловому недостатку его двойника.

Различные углы, связанные с Платоновыми телами, сведены в таблицу ниже. Численные значения телесных углов приведены в стерадианах . Константа φ = + √ 5/2 – 1 это золотое сечение .

Многогранник	двугранный угол ( я )	загар я / 2	Дефект ( д )	при вершине Телесный угол ( Ω )	Лицо твердый угол
тетраэдр	70.53°	$1 \over {\sqrt {2}}$	$\pi$	$\arccos \left({\frac {23}{27}}\right)\quad \approx 0.551286$	$\pi$
куб	90°	$1$	$\pi \over 2$	${\frac {\pi }{2}}\quad \approx 1.57080$	$2\pi \over 3$
октаэдр	109.47°	${\sqrt {2}}$	${2\pi } \over 3$	$4\arcsin \left({1 \over 3}\right)\quad \approx 1.35935$	$\pi \over 2$
додекаэдр	116.57°	$\varphi$	$\pi \over 5$	$\pi -\arctan \left({\frac {2}{11}}\right)\quad \approx 2.96174$	$\pi \over 3$
икосаэдр	138.19°	$\varphi ^{2}$	$\pi \over 3$	$2\pi -5\arcsin \left({2 \over 3}\right)\quad \approx 2.63455$	$\pi \over 5$

Радиусы, площади и объёмы

Еще одним достоинством регулярности является то, что все Платоновы тела обладают тремя концентрическими сферами:

• , описанная сфера проходящая через все вершины,
• , средняя сфера касающаяся каждого края в средней точке края, и
• , вписанная сфера касающаяся каждой грани в центре грани.

Радиусы и этих сфер называются описанным радиусом , средним радиусом внутренним радиусом . Это расстояния от центра многогранника до вершин, середин ребер и центров граней соответственно. Радиус описанной окружности R и внутренний радиус r твердого тела { p , q } с длиной ребра a определяются выражением

$${\begin{aligned}R&={\frac {a}{2}}\tan \left({\frac {\pi }{q}}\right)\tan \left({\frac {\theta }{2}}\right)\\[3pt]r&={\frac {a}{2}}\cot \left({\frac {\pi }{p}}\right)\tan \left({\frac {\theta }{2}}\right)\end{aligned}}$$

где θ — двугранный угол. Средний радиус ρ определяется выражением

$$\rho ={\frac {a}{2}}\cos \left({\frac {\pi }{p}}\right)\,{\csc }{\biggl (}{\frac {\pi }{h}}{\biggr )}$$

где h — величина, использованная выше при определении двугранного угла ( h = 4, 6, 6, 10 или 10). Отношение радиуса описанной окружности к внутреннему радиусу симметрично относительно p и q :

$${\frac {R}{r}}=\tan \left({\frac {\pi }{p}}\right)\tan \left({\frac {\pi }{q}}\right)={\frac {\sqrt {{\csc ^{2}}{\Bigl (}{\frac {\theta }{2}}{\Bigr )}-{\cos ^{2}}{\Bigl (}{\frac {\alpha }{2}}{\Bigr )}}}{\sin {\Bigl (}{\frac {\alpha }{2}}{\Bigr )}}}.$$

Площадь поверхности A -угольника на платонова тела { p , q } легко вычисляется как произведение площади правильного p количество F. граней Это:

$$A={\biggl (}{\frac {a}{2}}{\biggr )}^{2}Fp\cot \left({\frac {\pi }{p}}\right).$$

Объем умноженный вычисляется как F, на объем пирамиды , основанием которой является правильный p -угольник, а высотой – внутренний радиус r . То есть,

$$V={\frac {1}{3}}rA.$$

В следующей таблице перечислены различные радиусы платоновых тел, а также их площадь поверхности и объем. Общий размер фиксируется путем принятия длины ребра a равной 2.

Многогранник, а = 2	Радиус			Площадь поверхности, А	Объем
	В-, р	Середина-, р	Около-, R		V	Края блока
тетраэдр	$1 \over {\sqrt {6}}$	$1 \over {\sqrt {2}}$	${\sqrt {3 \over 2}}$	$4{\sqrt {3}}$	${\frac {\sqrt {8}}{3}}\approx 0.942809$	$\approx 0.117851$
куб	$1\,$	${\sqrt {2}}$	${\sqrt {3}}$	$24\,$	$8\,$	$1\,$
октаэдр	${\sqrt {2 \over 3}}$	$1\,$	${\sqrt {2}}$	$8{\sqrt {3}}$	${\frac {\sqrt {128}}{3}}\approx 3.771236$	$\approx 0.471404$
додекаэдр	${\frac {\varphi ^{2}}{\xi }}$	$\varphi ^{2}$	${\sqrt {3}}\,\varphi$	$12{\sqrt {25+10{\sqrt {5}}}}$	${\frac {20\varphi ^{3}}{\xi ^{2}}}\approx 61.304952$	$\approx 7.663119$
икосаэдр	${\frac {\varphi ^{2}}{\sqrt {3}}}$	$\varphi$	$\xi \varphi$	$20{\sqrt {3}}$	${\frac {20\varphi ^{2}}{3}}\approx 17.453560$	$\approx 2.181695$

Константы φ и ξ, указанные выше, определяются выражением

$$\varphi =2\cos {\pi \over 5}={\frac {1+{\sqrt {5}}}{2}},\qquad \xi =2\sin {\pi \over 5}={\sqrt {\frac {5-{\sqrt {5}}}{2}}}={\sqrt {3-\varphi }}.$$

Среди платоновых тел додекаэдр или икосаэдр можно рассматривать как лучшее приближение к сфере. Икосаэдр имеет наибольшее количество граней и наибольший двугранный угол, он наиболее плотно охватывает вписанную сферу, а отношение площади его поверхности к объему наиболее близко к соотношению сферы того же размера (т. е. либо той же площади поверхности, либо тот же объем). С другой стороны, додекаэдр имеет наименьший угловой дефект, самый большой телесный угол при вершине и больше всего заполняет описанную сферу.

Точка в пространстве

Для произвольной точки пространства платонова тела с радиусом описанной окружности R , расстояния которой до центра тяжести платонова тела и его n вершин равны L и d _i соответственно, и

$$S_{[n]}^{(2m)}={\frac {1}{n}}\sum _{i=1}^{n}d_{i}^{2m}$$

,

у нас есть

$${\begin{aligned}S_{[4]}^{(2)}=S_{[6]}^{(2)}=S_{[8]}^{(2)}=S_{[12]}^{(2)}=S_{[20]}^{(2)}&=R^{2}+L^{2},\\[4px]S_{[4]}^{(4)}=S_{[6]}^{(4)}=S_{[8]}^{(4)}=S_{[12]}^{(4)}=S_{[20]}^{(4)}&=\left(R^{2}+L^{2}\right)^{2}+{\frac {4}{3}}R^{2}L^{2},\\[4px]S_{[6]}^{(6)}=S_{[8]}^{(6)}=S_{[12]}^{(6)}=S_{[20]}^{(6)}&=\left(R^{2}+L^{2}\right)^{3}+4R^{2}L^{2}\left(R^{2}+L^{2}\right),\\[4px]S_{[12]}^{(8)}=S_{[20]}^{(8)}&=\left(R^{2}+L^{2}\right)^{4}+8R^{2}L^{2}\left(R^{2}+L^{2}\right)^{2}+{\frac {16}{5}}R^{4}L^{4},\\[4px]S_{[12]}^{(10)}=S_{[20]}^{(10)}&=\left(R^{2}+L^{2}\right)^{5}+{\frac {40}{3}}R^{2}L^{2}\left(R^{2}+L^{2}\right)^{3}+16R^{4}L^{4}\left(R^{2}+L^{2}\right).\end{aligned}}$$

Для всех пяти Платоновых тел мы имеем

$$S_{[n]}^{(4)}+{\frac {16}{9}}R^{4}=\left(S_{[n]}^{(2)}+{\frac {2}{3}}R^{2}\right)^{2}.$$

Если d _i — расстояния от n вершин платонова тела до любой точки описанной им сферы, то

$$4\left(\sum _{i=1}^{n}d_{i}^{2}\right)^{2}=3n\sum _{i=1}^{n}d_{i}^{4}.$$

Собственность Руперта

многогранник P Говорят, что обладает свойством Руперта , если многогранник того же или большего размера и той же формы, что и P, пройти через отверстие в P. может Этим свойством обладают все пять Платоновых тел.

Симметрия

Двойные многогранники

Двойные соединения

Каждый многогранник имеет двойственный (или «полярный») многогранник с перепутанными гранями и вершинами . Двойником каждого Платонова тела является другое Платоново тело, так что мы можем расположить пять тел в двойственные пары.

• Тетраэдр самодуален (т.е. ему двойственным является другой тетраэдр).
• Куб и октаэдр образуют двойственную пару.
• Додекаэдр и икосаэдр образуют двойственную пару.

Если многогранник имеет символ Шлефли { p , q }, то его двойственный многогранник имеет символ { q , p }. Действительно, каждое комбинаторное свойство одного Платонова тела можно интерпретировать как другое комбинаторное свойство двойственного.

Двойственный многогранник можно построить, приняв вершины двойственного многогранника за центры граней исходной фигуры. Соединение центров соседних граней в оригинале образует ребра двойственной и тем самым меняет местами количество граней и вершин, сохраняя при этом количество ребер.

В более общем смысле, можно дуализировать платоново тело относительно сферы радиуса d, концентрической с телом. Радиусы ( R , ρ , r ) твердого тела и радиусы двойственного ему тела ( R *, ρ *, r *) связаны соотношением

$$d^{2}=R^{\ast }r=r^{\ast }R=\rho ^{\ast }\rho .$$

Дуализация по средней сфере ( d = ρ ) часто удобна, поскольку средняя сфера имеет одинаковое отношение к обоим многогранникам. Принимая д ² = Rr дает двойное твердое тело с одинаковым радиусом описанной и внутренней окружности (т.е. R * = R и r * = r ).

Группы симметрии

В математике понятие симметрии изучается с помощью понятия математической группы . Каждый многогранник имеет связанную с ним группу симметрии , которая представляет собой набор всех преобразований ( евклидовых изометрий ), которые оставляют многогранник инвариантным. Порядок группы симметрии — это число симметрий многогранника. Часто различают полную группу симметрии , включающую отражения , и собственную группу симметрии , включающую только вращения .

Группы симметрии Платоновых тел представляют собой особый класс трехмерных точечных групп, известных как многогранные группы . Высокую степень симметрии Платоновых тел можно интерпретировать по-разному. Самое главное, что вершины каждого тела эквивалентны под действием группы симметрии, как и ребра и грани. Говорят, что действие группы симметрии транзитивно на вершинах, ребрах и гранях. Фактически, это еще один способ определения правильности многогранника: многогранник является правильным тогда и только тогда, когда он однороден по вершинам , однороден по ребрам и однороден по граням .

С платоновыми телами связаны только три группы симметрии, а не пять, поскольку группа симметрии любого многогранника совпадает с группой симметрии двойственного ему многогранника. В этом легко убедиться, рассмотрев конструкцию двойственного многогранника. Любая симметрия оригинала должна быть симметрией двойственного и наоборот. Три многогранные группы:

• тетраэдрическая группа Т ,
• октаэдрическая группа O (которая также является группой симметрии куба) и
• группа икосаэдра I (которая также является группой симметрии додекаэдра).

Порядки собственных групп (вращения) равны 12, 24 и 60 соответственно — ровно в два раза больше числа ребер в соответствующих многогранниках. Порядки полных групп симметрии снова вдвое больше (24, 48 и 120). См. (Coxeter 1973) вывод этих фактов. Все Платоновы тела, за исключением тетраэдра, центрально симметричны, то есть сохраняются при отражении через начало координат .

В следующей таблице перечислены различные свойства симметрии платоновых тел. Перечисленные группы симметрии представляют собой полные группы с подгруппами вращения, указанными в скобках (аналогично количеству симметрий). Конструкция калейдоскопа Витгофа — это метод построения многогранников непосредственно из их групп симметрии. Они перечислены для справки по символу Витхоффа для каждого из Платоновых тел.

Многогранник	Шлефли символ	Витхофф символ	Двойной многогранник	Группа симметрии (отражение, вращение)
				Многогранник	Хороший.	Кокс.	Орб.	Заказ
тетраэдр	{3, 3}	3 | 2 3	тетраэдр	Тетраэдрический	Т д Т	[3,3] [3,3] +	*332 332	24 12
куб	{4, 3}	3 | 2 4	октаэдр	Октаэдрический	Ой ​ ТО	[4,3] [4,3] +	*432 432	48 24
октаэдр	{3, 4}	4 | 2 3	куб
додекаэдр	{5, 3}	3 | 2 5	икосаэдр	икосаэдрический	I h я	[5,3] [5,3] +	*532 532	120 60
икосаэдр	{3, 5}	5 | 2 3	додекаэдр

В природе и технике

Тетраэдр, куб и октаэдр естественным образом встречаются в кристаллических структурах . Этим ни в коем случае не исчерпывается число возможных форм кристаллов. Однако среди них нет ни правильного икосаэдра, ни правильного додекаэдра. Одна из форм, названная пиритоэдром (по имени группы минералов , для которой она типична), имеет двенадцать пятиугольных граней, расположенных по тому же принципу, что и грани правильного додекаэдра. Однако грани пиритоэдра неправильные, поэтому пиритоэдр тоже неправильный. Аллотропы бора и многих соединений бора , таких как карбид бора , включают в себя дискретные икосаэдры B ₁₂ внутри своих кристаллических структур. Карборановые кислоты также имеют молекулярную структуру, приближающуюся к правильным икосаэдрам.

Циргониевые икосаэдры — разновидность радиолярий , по форме напоминающая правильный икосаэдр .

В начале 20 века Эрнст Геккель описал (Haeckel, 1904) ряд видов радиолярий , скелеты некоторых из которых имеют форму различных правильных многогранников. Примеры включают Circoporus октаэдр , Circogonia икосаэдры , Lithocubus геометрический и Circorregma dodecahedra . Формы этих существ должны быть очевидны из их названий.

Многие вирусы , такие как герпес вирус, имеют форму правильного икосаэдра. Вирусные структуры построены из повторяющихся идентичных белковых субъединиц, и икосаэдр — самая простая форма для сборки с использованием этих субъединиц. Правильный многогранник используется потому, что его можно построить из одной базовой единицы белка, используемой снова и снова; это экономит место в вирусном геноме .

В метеорологии и климатологии все больший интерес вызывают глобальные численные модели атмосферных потоков, в которых используются геодезические сетки , основанные на икосаэдре (уточненном триангуляцией ) вместо более часто используемой сетки долготы / широты . Преимущество этого метода состоит в равномерном распределении пространственного разрешения без сингулярностей (т.е. полюсов) за счет несколько большей вычислительной сложности.

Икосаэдр как часть памятника Спинозе в Амстердаме

Геометрия пространственных рамок часто основана на платоновых телах. В системе MERO Платоновы тела используются для обозначения различных конфигураций пространственных рамок. Например, 1/2 T относится к конфигурации , O + состоящей из половины октаэдра и тетраэдра.

несколько платоновых углеводородов Было синтезировано , в том числе кубан и додекаэдр , но не тетраэдран .

• 
  Тетраэдр
• 
  Кубинский
• 
  Додекаэдр

Набор многогранных игральных костей.

Платоновы тела часто используются для изготовления игральных костей , поскольку игральные кости такой формы можно сделать справедливыми . Шестигранные игральные кости очень распространены, но в ролевых играх обычно используются и другие числа . Такие игральные кости обычно обозначаются как d n, где n — количество граней (d8, d20 и т. д.); см . в обозначении кубиков более подробную информацию .

Эти формы часто встречаются в других играх или головоломках. Головоломки, похожие на кубик Рубика, бывают всех пяти форм – см. волшебные многогранники .

платоновых

Для промежуточной материальной фазы, называемой жидкими кристаллами , существование такой симметрии было впервые предложено в 1981 году Х. Кляйнертом и К. Маки. В алюминии икосаэдрическая структура была открыта через три года после этого Дэном Шехтманом , что принесло ему Нобелевскую премию по химии в 2011 году.

Связанные многогранники и многогранники

Однородные многогранники

Существуют четыре правильных многогранника, которые не являются выпуклыми, которые называются многогранниками Кеплера – Пуансо . Все они имеют икосаэдрическую симметрию и могут быть получены как звездочки додекаэдра и икосаэдра.

кубооктаэдр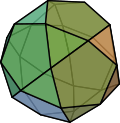

икосододекаэдр

Следующими наиболее правильными выпуклыми многогранниками после Платоновых тел являются кубооктаэдр , являющийся спрямлением куба и октаэдра, и икосододекаэдр , являющийся спрямлением додекаэдра и икосаэдра (спрямление самодвойственного тетраэдра - это правильный октаэдр). Оба они квазирегулярны , что означает, что они однородны по вершинам и ребрам и имеют правильные грани, но не все грани конгруэнтны (относятся к двум разным классам). Они образуют два из тринадцати архимедовых тел , которые представляют собой выпуклые однородные многогранники с многогранной симметрией. Их двойники, ромбический додекаэдр и ромбический триаконтаэдр , транзитивны по ребрам и граням, но их грани не являются правильными, и каждая из их вершин бывает двух типов; это два из тринадцати каталонских тел .

Однородные многогранники образуют гораздо более широкий класс многогранников. Эти фигуры являются однородными по вершинам и имеют один или несколько типов правильных или звездчатых многоугольников для граней. К ним относятся все упомянутые выше многогранники вместе с бесконечным набором призм , бесконечным набором антипризм и 53 другими невыпуклыми формами.

Твердые тела Джонсона представляют собой выпуклые многогранники с правильными гранями, но не однородные. Среди них пять из восьми выпуклых дельтаэдров , имеющих одинаковые правильные грани (все равносторонние треугольники), но не однородные. (Другие три выпуклых дельтаэдра — это платонов тетраэдр, октаэдр и икосаэдр.)

Обычные тесселяции

Регулярные сферические мозаики

Платонический
{3,3}	{4,3}	{3,4}	{5,3}	{3,5}
Правильный двугранник
{2,2}	{3,2}	{4,2}	{5,2}	{6,2}...
Правильный одногранник
{2,2}	{2,3}	{2,4}	{2,5}	{2,6}...

Три регулярных мозаики плоскости тесно связаны с Платоновыми телами. Действительно, можно рассматривать Платоновы тела как регулярные мозаики сферы . Это делается путем проецирования каждого твердого тела на концентрическую сферу. Грани проецируются на правильные сферические многоугольники , которые точно покрывают сферу. Сферические мозаики образуют два бесконечных дополнительных набора правильных мозаик: осоэдры {2, n } с двумя вершинами в полюсах и лунными гранями, а также двойственные диэдры { n ,2} с двумя полусферическими гранями и регулярно расположенными вершинами на экватор. Такие мозаики были бы вырождены в истинном трехмерном пространстве как многогранники.

Каждая регулярная мозаика сферы характеризуется парой целых чисел { p , q } с 1 / п + 1 / кв > 1/2 ​ ​ . Аналогично регулярное замощение плоскости характеризуется условием 1 / п + 1 / д = 1/2 ​ ​ . Есть три возможности:

Три правильных мозаики евклидовой плоскости

{4, 4}	{3, 6}	{6, 3}

Аналогичным образом можно рассматривать регулярные мозаики гиперболической плоскости . Для них характерно состояние 1 / п + 1 / q < 1/2 ​ ​ . Существует бесконечное семейство таких мозаик.

Пример регулярных мозаик гиперболической плоскости

{5, 4}	{4, 5}	{7, 3}	{3, 7}

Высшие измерения

Дополнительная информация: Список правильных многогранников.

Количество измерений	Количество выпуклых правильных многогранников
0	1
1	1
2	∞
3	5
4	6
> 4	3

В более чем трёх измерениях многогранники обобщаются до многогранников , причем многомерные выпуклые правильные многогранники являются эквивалентами трёхмерных Платоновых тел.

В середине 19 века швейцарский математик Людвиг Шлефли открыл четырехмерные аналоги Платоновых тел, названные выпуклыми правильными 4-многогранниками . Таких фигур ровно шесть; пять аналогичны Платоновым телам: 5-ячеечное как {3,3,3}, 16-ячеечное как {3,3,4}, 600-ячеечное как {3,3,5}, тессеракт как {4,3 ,3}, и 120-ячеечный как {5,3,3}, и шестой, самодвойственный 24-клеточный , {3,4,3}.

Во всех измерениях выше четырех существует только три выпуклых правильных многогранника: симплекс { 3,3,...,3}, гиперкуб {4,3,...,3} и перекрестный многогранник . как {3,3,...,4}. В трех измерениях они совпадают с тетраэдром как {3,3}, кубом как {4,3} и октаэдром как {3,4}.

См. также

• Архимедово тело
• Каталонский солид
• Дельтаэдр
• Джонсон твердый
• Многогранник Гольдберга
• Многогранник Кеплера-Пуансо
• Список правильных многогранников
• Куб принца Руперта
• Правильный многогранник
• Правильный косой многогранник
• Тороидальный многогранник

Общие и цитируемые источники

• Атья, Майкл ; Сатклифф, Пол (2003). «Многогранники в физике, химии и геометрии». Милан Дж. Математика . 71 : 33–58. arXiv : math-ph/0303071 . Бибкод : 2003math.ph...3071A . дои : 10.1007/s00032-003-0014-1 . S2CID   119725110 .
• Бойер, Карл ; Мерцбах, Ута (1989). История математики (2-е изд.). Уайли. ISBN  0-471-54397-7 .
• Коксетер, HSM (1973). Правильные многогранники (3-е изд.). Нью-Йорк: Dover Publications. ISBN  0-486-61480-8 .
• Евклид (1956). Хит, Томас Л. (ред.). Тринадцать книг «Элементов Евклида», книги 10–13 (2-е неизданное изд.). Нью-Йорк: Dover Publications. ISBN  0-486-60090-4 .
• Гарднер, Мартин (1987). 2-я книга математических головоломок и развлечений Scientific American , University of Chicago Press, Глава 1: Пять Платоновых тел, ISBN   0226282538
• Геккель, Эрнст , Э. (1904). Художественные формы природы . Доступно как Геккель, Э. (1998); Формы искусства в природе , Престель США. ISBN   3-7913-1990-6 .
• Кеплер. Йоханнес Стрена seu de nive sexangula (О шестиугольной снежинке) , статья Кеплера 1611 года, в которой обсуждается причина шестиугольной формы снежных кристаллов, а также формы и симметрии в природе. Рассказывает о платоновых телах.
• Кляйнерт, Хаген и Маки, К. (1981). «Решеточные текстуры в холестерических жидких кристаллах» (PDF) . Достижения физики . 29 (5): 219–259. Бибкод : 1981ForPh..29..219K . дои : 10.1002/prop.19810290503 .
• Ллойд, Дэвид Роберт (2012). «Сколько лет Платоновым Телам?». Бюллетень BSHM: Журнал Британского общества истории математики . 27 (3): 131–140. дои : 10.1080/17498430.2012.670845 . S2CID   119544202 .
• Пью, Энтони (1976). Многогранники: визуальный подход . Калифорния: Издательство Калифорнийского университета в Беркли. ISBN  0-520-03056-7 .
• Вейль, Герман (1952). Симметрия . Принстон, Нью-Джерси: Издательство Принстонского университета. ISBN  0-691-02374-3 .
• Вильдберг, Кристиан (1988). Критика Иоанном Филопоном теории эфира Аристотеля . Вальтер де Грюйтер. стр. 11–12. ISBN   9783110104462 .

Внешние ссылки

• Платоновые тела в математической энциклопедии
• Вайсштейн, Эрик В. «Платоновое тело» . Математический мир .
• Вайсштейн, Эрик В. «Изоэдр» . Математический мир .
• Книга XIII Евклида «Начал» .
• Интерактивные 3D-многогранники на Java
• Платоновые тела в визуальных многогранниках
• Solid Body Viewer — это интерактивный просмотрщик 3D-многогранников, который позволяет сохранять модель в формате svg, stl или obj.
• Интерактивное складывание/разворачивание платоновых тел. Архивировано 9 февраля 2007 г. на Wayback Machine на Java.
• Бумажные модели Платоновых тел, созданные с использованием сетей, созданных в Stella . программном обеспечении
• Платоновые тела Бесплатные бумажные модели (сетки)
• Грайм, Джеймс; Стеклс, Кэти. «Платоновые тела» . Числофил . Брэйди Харан . Архивировано из оригинала 23 октября 2018 г. Проверено 13 апреля 2013 г.
• Преподавание математики с помощью моделей искусства, созданных учащимися
• Обучение математике с инструкциями учителя рисования по изготовлению моделей
• Фреймы изображений платоновых тел алгебраических поверхностей
• Платоновые тела с некоторыми выводами формул
• Как сделать из куба четыре платоновых тела