Теорема о биссектрисе угла

В геометрии теорема о биссектрисе угла касается относительных длин двух сегментов , на которые сторона треугольника разделена линией , делящей противоположный угол пополам . Он приравнивает их относительные длины к относительным длинам двух других сторон треугольника.

Теорема [ править ]

Рассмотрим треугольник $△ ABC$ . Пусть биссектриса угла $∠ A$ пересекает сторону $BC$ в точке $D$ между $B$ и $C$ . Теорема о биссектрисе угла гласит, что отношение длины отрезка BD $к$ длине отрезка $CD$ равно отношению длины стороны $AB$ к длине стороны $AC$ :

{\frac {|BD|}{|CD|}}={\frac {|AB|}{|AC|}},

и наоборот , если точка $D$ на стороне $BC$ треугольника $△ ABC$ делит $BC$ что и стороны $AB$ и $AC$ , то $AD$ является биссектрисой угла $∠ A.$ в том же отношении ,

Обобщенная теорема о биссектрисе утверждает, что если $D$ лежит на прямой $BC$ , то

{\frac {|BD|}{|CD|}}={\frac {|AB|\sin \angle DAB}{|AC|\sin \angle DAC}}.

Это сводится к предыдущей версии, если $AD$ является биссектрисой $∠ BAC$ . Когда $D$ является внешним по отношению к сегменту $BC$ , в расчете необходимо использовать направленные отрезки линий и направленные углы.

Теорема о биссектрисе угла обычно используется, когда известны биссектрисы угла и длины сторон. Его можно использовать при расчете или доказательстве.

Непосредственным следствием теоремы является то, что биссектриса угла при вершине равнобедренного треугольника также делит пополам противоположную сторону.

Доказательства [ править ]

Существует множество различных способов доказательства теоремы о биссектрисе. Некоторые из них показаны ниже.

Доказательство с использованием подобных треугольников [ править ]

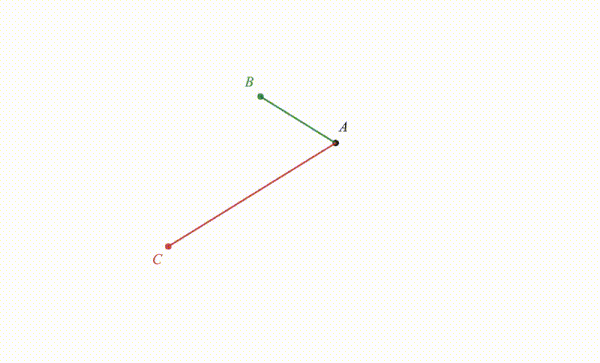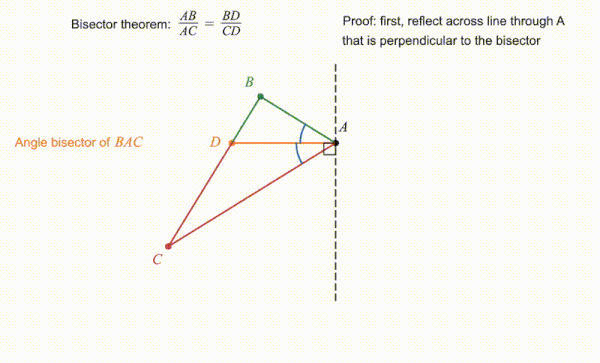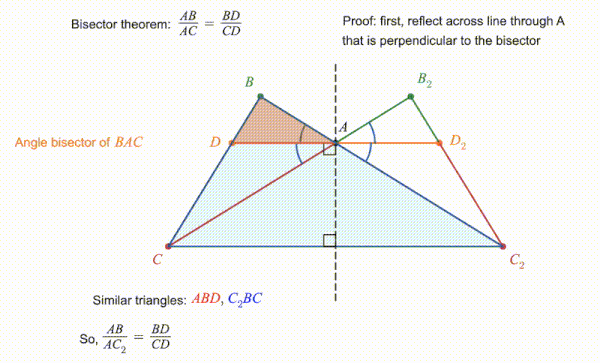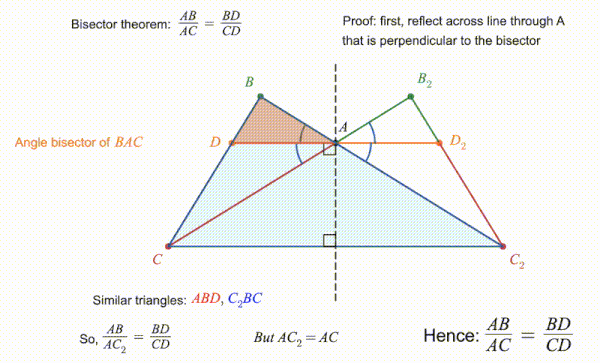
Как показано на сопровождающей анимации, теорему можно доказать, используя подобные треугольники. В показанной здесь версии треугольник $\triangle ABC$ отражается от линии, перпендикулярной биссектрисе угла. $AD$ , в результате чего получается треугольник $\triangle AB_{2}C_{2}$ с биссектрисой $AD_{2}$ . Тот факт, что углы, образованные биссектрисой $\angle BAD$ и $\angle CAD$ равны, означает, что $BAC_{2}$ и $CAB_{2}$ представляют собой прямые линии. Это позволяет построить треугольник $\triangle C_{2}BC$ это похоже на $\triangle ABD$ . Поскольку отношения между соответствующими сторонами подобных треугольников равны, отсюда следует, что $|AB|/|AC_{2}|=|BD|/|CD|$ . Однако, $AC_{2}$ был построен как отражение линии $AC$ , и поэтому эти две строки имеют одинаковую длину. Поэтому, $|AB|/|AC|=|BD|/|CD|$ , что дает результат, сформулированный теоремой.

синусов Доказательство с использованием закона

На приведенной выше схеме используйте закон синусов для треугольников $△ ABD$ и $△ ACD$ :

{\frac {|AB|}{|BD|}}={\frac {\sin \angle ADB}{\sin \angle DAB}}

( 1 )

{\frac {|AC|}{|CD|}}={\frac {\sin \angle ADC}{\sin \angle DAC}}

( 2 )

Углы $∠ADB ∠ADC$ и $углами дополнительными$ то есть являются смежными . образуют линейную пару , Поскольку дополнительные углы имеют равные синусы,

{\sin \angle ADB}={\sin \angle ADC}.

Углы $∠ DAB$ и $∠ DAC$ равны. Следовательно, правые части уравнений ( 1 ) и ( 2 ) равны, поэтому их левые части также должны быть равны.

{\frac {|BD|}{|CD|}}={\frac {|AB|}{|AC|}},

что является теоремой о биссектрисе угла.

Если углы $∠ DAB, ∠ DAC$ неравны, уравнения ( 1 ) и ( 2 ) можно переписать как:

{{\frac {|AB|}{|BD|}}\sin \angle DAB=\sin \angle ADB},

{{\frac {|AC|}{|CD|}}\sin \angle DAC=\sin \angle ADC}.

Углы $∠ ADB, ∠ ADC$ по-прежнему являются дополнительными, поэтому правые части этих уравнений по-прежнему равны, поэтому получаем:

{{\frac {|AB|}{|BD|}}\sin \angle DAB={\frac {|AC|}{|CD|}}\sin \angle DAC},

что переводится в «обобщенную» версию теоремы.

Доказательство с использованием высот треугольников [ править ]

Пусть $D$ — точка на прямой $BC$ , не равная $B$ или $C$ и такая, что $AD$ не является высотой треугольника $△ ABC$ .

Пусть $B 1$ — основание (фут) высоты в треугольнике $△ ABD$ через $B$ , и пусть $C 1$ — основание высоты в треугольнике $△ ACD$ через $C$ . Тогда, если $D$ находится строго между $B$ и $C$ , один и только один из $B1 внутри$ или $C1,$ лежит внутри $△ ABC$ можно предположить , и без ограничения общности что $B1 лежит$ . Этот случай изображен на соседней диаграмме. Если $D$ лежит вне отрезка $BC$ , то ни $B1,$ ни $C1 не$ лежат внутри треугольника.

$∠ DB 1 B, ∠ DC 1 C$ — прямые углы, а углы $∠ B 1 DB, ∠ C 1 DC$ равны, если $D$ лежит на отрезке $BC$ (т. е. между $B$ и $C$ ) и одинаковы в остальных рассматриваемых случаях, поэтому треугольники $△ DB 1 B, △ DC 1 C$ подобны (ААА), из чего следует, что:

{\frac {|BD|}{|CD|}}={\frac {|BB_{1}|}{|CC_{1}|}}={\frac {|AB|\sin \angle BAD}{|AC|\sin \angle CAD}}.

Если $D$ — подножие высоты, то

{\frac {|BD|}{|AB|}}=\sin \angle \ BAD{\text{ and }}{\frac {|CD|}{|AC|}}=\sin \angle \ DAC,

и следует обобщенная форма.

Доказательство с использованием треугольных областей [ править ]

взглянув на соотношение площадей двух треугольников $△ BAD, △ CAD$ , которые образованы биссектрисой угла $A.$ Быстрое доказательство можно получить , Вычисление этих площадей дважды по разным формулам , то есть ${\tfrac {1}{2}}gh$ с основанием $g$ и высотой $h$ и ${\tfrac {1}{2}}ab\sin(\gamma )$ со сторонами $a, b$ и приложенным к ним углом $γ$ , даст желаемый результат.

Обозначим через $h$ высоту треугольников основания $BC$ и $\alpha$ быть половиной угла в $A$ . Затем

{\frac {|\triangle ABD|}{|\triangle ACD|}}={\frac {{\frac {1}{2}}|BD|h}{{\frac {1}{2}}|CD|h}}={\frac {|BD|}{|CD|}}

и

{\frac {|\triangle ABD|}{|\triangle ACD|}}={\frac {{\frac {1}{2}}|AB||AD|\sin(\alpha )}{{\frac {1}{2}}|AC||AD|\sin(\alpha )}}={\frac {|AB|}{|AC|}}

урожайность

{\frac {|BD|}{|CD|}}={\frac {|AB|}{|AC|}}.

Длина биссектрисы угла [ править ]

Длина биссектрисы угла $d$ можно найти по ${\textstyle d^{2}=bc-mn=mn(k^{2}-1)=bc\left(1-{\frac {1}{k^{2}}}\right)}$ ,

где $k={\frac {b}{n}}={\frac {c}{m}}={\frac {b+c}{a}}$ – константа пропорциональности из теоремы о биссектрисе угла.

Доказательство : По теореме Стюарта имеем

${\begin{aligned}b^{2}m+c^{2}n&=a(d^{2}+mn)\\(kn)^{2}m+(km)^{2}n&=a(d^{2}+mn)\\k^{2}(m+n)mn&=(m+n)(d^{2}+mn)\\k^{2}mn&=d^{2}+mn\\(k^{2}-1)mn&=d^{2}\\\end{aligned}}$

Биссектрисы внешнего угла [ править ]

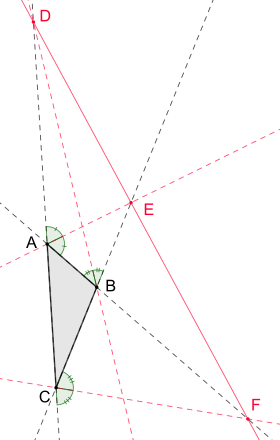
биссектрисы внешнего угла (красные точки):
Точки $D, E, F$ лежат на одной прямой, и выполняются следующие уравнения для отношений:
${\tfrac {|EB|}{|EC|}}={\tfrac {|AB|}{|AC|}}$ , ${\tfrac {|FB|}{|FA|}}={\tfrac {|CB|}{|CA|}}$ , ${\tfrac {|DA|}{|DC|}}={\tfrac {|BA|}{|BC|}}$

Для биссектрис внешних углов неравностороннего треугольника существуют аналогичные уравнения для отношений длин сторон треугольника. Точнее, если биссектриса внешнего угла в $A$ пересекает расширенную сторону $BC$ в $E$ , биссектриса внешнего угла в $B$ пересекает расширенную сторону $AC$ в $D$ , а биссектриса внешнего угла в $C$ пересекает расширенную сторону $AB$ в $F$ , то выполняются следующие уравнения : ^[1]

{\frac {|EB|}{|EC|}}={\frac {|AB|}{|AC|}}

,

{\frac {|FB|}{|FA|}}={\frac {|CB|}{|CA|}}

,

{\frac {|DA|}{|DC|}}={\frac {|BA|}{|BC|}}

Три точки пересечения биссектрис внешнего угла и продолженных сторон треугольника $D, E, F$ коллинеарны, то есть лежат на одной прямой. ^[2]

История [ править ]

Теорема о биссектрисе угла появляется в предложении 3 книги VI « Начал» Евклида . Согласно Хиту (1956 , стр. 197 (т. 2)), соответствующее утверждение для биссектрисы внешнего угла было дано Робертом Симсоном, который отметил, что Папп предположил этот результат без доказательства. Далее Хит говорит, что Огастес Де Морган предложил объединить эти два утверждения следующим образом: ^[3]

Если угол треугольника делится пополам внутри или снаружи прямой линией, которая разрезает противоположную сторону или полученную противоположную сторону, сегменты этой стороны будут иметь то же соотношение, что и другие стороны треугольника; и если сторона треугольника разделена внутри или снаружи так, что ее сегменты имеют то же соотношение, что и другие стороны треугольника, то прямая линия, проведенная от точки сечения до угловой точки, противоположной первой упомянутой стороне, разделит внутренний или внешний угол пополам в этой угловой точке.

Приложения [ править ]

Эта теорема была использована для доказательства следующих теорем/результатов:

Координаты центра треугольника
Круги Аполлония

Ссылки [ править ]

^ Альфред С. Посаментье: Расширенная евклидова геометрия: Экскурсии для студентов и учителей . Спрингер, 2002 г., ISBN 9781930190856 , стр. 3–4.
^ Роджер А. Джонсон: Расширенная евклидова геометрия . Дувр 2007, ISBN 978-0-486-46237-0 , с. 149 (оригинальная публикация 1929 года совместно с Houghton Mifflin Company (Бостон) под названием Modern Geometry ).
^ Хит, Томас Л. (1956). Тринадцать книг «Элементов Евклида» (2-е изд. [Факсимиле. Оригинальная публикация: Cambridge University Press, 1925] изд.). Нью-Йорк: Dover Publications.
(3 тома): ISBN 0-486-60088-2 (т. 1), ISBN 0-486-60089-0 (т. 2), ISBN 0-486-60090-4 (т. 3). Авторитетный перевод Хита, а также обширные исторические исследования и подробные комментарии по всему тексту.

Дальнейшее чтение [ править ]

GWIS Амарасингхе: О стандартных длинах биссектрис и теореме о биссектрисе угла , Глобальный журнал перспективных исследований классической и современной геометрии, том 01 (01), стр. 15–27, 2012 г.

Внешние ссылки [ править ]

[1] Альфред С. Посаментье: Расширенная евклидова геометрия: Экскурсии для студентов и учителей . Спрингер, 2002 г., ISBN 9781930190856 , стр. 3–4.

[2] Роджер А. Джонсон: Расширенная евклидова геометрия . Дувр 2007, ISBN 978-0-486-46237-0 , с. 149 (оригинальная публикация 1929 года совместно с Houghton Mifflin Company (Бостон) под названием Modern Geometry ).

[3] Хит, Томас Л. (1956). Тринадцать книг «Элементов Евклида» (2-е изд. [Факсимиле. Оригинальная публикация: Cambridge University Press, 1925] изд.). Нью-Йорк: Dover Publications.
(3 тома): ISBN 0-486-60088-2 (т. 1), ISBN 0-486-60089-0 (т. 2), ISBN 0-486-60090-4 (т. 3). Авторитетный перевод Хита, а также обширные исторические исследования и подробные комментарии по всему тексту.

[1]

[2]

[3]