Круги Аполлония

Круги Аполлония — это один из нескольких наборов кругов, связанных с Аполлонием Пергским , известным греческим геометром . Большинство этих кругов встречаются в плоской евклидовой геометрии , но аналоги были определены и на других поверхностях; например, аналоги на поверхности сферы можно определить с помощью стереографической проекции .

У этого термина пять основных применений:

1. Аполлоний показал, что круг можно определить как набор точек на плоскости, которые имеют определенное соотношение расстояний до двух фиксированных точек, известных как фокусы . Этот аполлонический круг является основой проблемы преследования Аполлония. Это частный случай первого семейства, описанного в №2.
2. Аполлоновы круги — это два семейства взаимно ортогональных кругов. Первое семейство состоит из кругов со всеми возможными соотношениями расстояний до двух фиксированных фокусов (те же круги, что и в № 1), тогда как второе семейство состоит из всех возможных кругов, проходящих через оба фокуса. Эти круги составляют основу биполярных координат .
3. Окружности Аполлония треугольника представляют собой три окружности, каждая из которых проходит через одну вершину треугольника и сохраняет постоянное соотношение расстояний до двух других. Изодинамические точки и линию Лемуана треугольника можно решить с помощью этих кругов Аполлония.
4. Задача Аполлония состоит в том, чтобы построить окружности, одновременно касающиеся трех заданных окружностей. Пути решения этой проблемы иногда называют кругами Аполлония .
5. Аполлоническая прокладка — один из первых когда-либо описанных фракталов — представляет собой набор взаимно касающихся кругов, образованных в результате итеративного решения проблемы Аполлония.

Определение круга Аполлонием

Основная статья: Круг § Круг Аполлония

Рисунок 1. Определение круга Аполлонием.

Круг обычно определяется как набор точек P на заданном расстоянии r (радиус круга) от заданной точки (центра круга). Однако существуют и другие эквивалентные определения круга. Аполлоний обнаружил, что круг можно определить как множество точек P , имеющих заданное соотношение расстояний k = d ₁ / d ₂ к двум заданным точкам (обозначенным A и B на рисунке 1). Эти две точки иногда называют фокусами .

с использованием векторов в

Пусть d ₁ , d ₂ — неравные положительные действительные числа.Пусть C — внутренняя точка разделения AB в соотношении d ₁ : d ₂ , а D — внешняя точка разделения AB в том же соотношении d ₁ : d ₂ .

${\overrightarrow {\mathrm {PC} }}={\frac {d_{2}{\overrightarrow {\mathrm {PA} }}+d_{1}{\overrightarrow {\mathrm {PB} }}}{d_{2}+d_{1}}},\ {\overrightarrow {\mathrm {PD} }}={\frac {d_{2}{\overrightarrow {\mathrm {PA} }}-d_{1}{\overrightarrow {\mathrm {PB} }}}{d_{2}-d_{1}}}.$

Затем,

${\begin{aligned}&\mathrm {PA} :\mathrm {PB} =d_{1}:d_{2}.\\\Leftrightarrow {}&d_{2}|{\overrightarrow {\mathrm {PA} }}|=d_{1}|{\overrightarrow {\mathrm {PB} }}|.\\\Leftrightarrow {}&d_{2}^{2}|{\overrightarrow {\mathrm {PA} }}|^{2}=d_{1}^{2}|{\overrightarrow {\mathrm {PB} }}|^{2}.\\\Leftrightarrow {}&(d_{2}{\overrightarrow {\mathrm {PA} }}+d_{1}{\overrightarrow {\mathrm {PB} }})\cdot (d_{2}{\overrightarrow {\mathrm {PA} }}-d_{1}{\overrightarrow {\mathrm {PB} }})=0.\\\Leftrightarrow {}&{\frac {d_{2}{\overrightarrow {\mathrm {PA} }}+d_{1}{\overrightarrow {\mathrm {PB} }}}{d_{2}+d_{1}}}\cdot {\frac {d_{2}{\overrightarrow {\mathrm {PA} }}-d_{1}{\overrightarrow {\mathrm {PB} }}}{d_{2}-d_{1}}}=0.\\\Leftrightarrow {}&{\overrightarrow {\mathrm {PC} }}\cdot {\overrightarrow {\mathrm {PD} }}=0.\\\Leftrightarrow {}&{\overrightarrow {\mathrm {PC} }}={\vec {0}}\vee {\overrightarrow {\mathrm {PD} }}={\vec {0}}\vee {\overrightarrow {\mathrm {PC} }}\perp {\overrightarrow {\mathrm {PD} }}.\\\Leftrightarrow {}&\mathrm {P} =\mathrm {C} \vee \mathrm {P} =\mathrm {D} \vee \angle {\mathrm {CPD} }=90^{\circ }.\end{aligned}}$

Следовательно, точка P находится на окружности диаметром CD .

Доказательство с использованием теоремы о биссектрисе

Доказательство определения круга, данного Аполлонием.

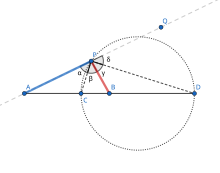
Сначала рассмотрим точку $C$ на отрезке между $A$ и $B$, удовлетворяющее соотношению. По определению

$${\frac {|AP|}{|BP|}}={\frac {|AC|}{|BC|}}$$

и согласно обратной углы теореме о биссектрисе $\alpha =\angle APC$ и $\beta =\angle CPB$ равны.

Далее возьмем другую точку $D$ на расширенной линии $AB$ что удовлетворяет соотношению. Так

$${\frac {|AP|}{|BP|}}={\frac {|AD|}{|BD|}}.$$

Также возьмем еще какой-нибудь момент $Q$ где угодно на расширенной линии $AP$. Опять же, согласно обратной теореме о биссектрисе, линия $PD$ делит внешний угол пополам $\angle QPB$. Следовательно, $\gamma =\angle BPD$ и $\delta =\angle QPD$ равны и $\beta +\gamma =90^{\circ }$. Следовательно, по теореме Фалеса $P$ лежит на круге, имеющем $CD$ как диаметр.

преследования

ли корабль, выходящий из одной точки A со скоростью v _A перехватит , другой корабль, выходящий из другой точки B со скоростью v _B. Задача преследования Аполлония состоит в том, чтобы выяснить , Минимальное время перехвата двух кораблей рассчитывается по прямолинейным траекториям. Если скорости кораблей остаются постоянными, их соотношение скоростей определяется μ. Если оба корабля столкнутся или встретятся в будущей точке I , то расстояния каждого из них связаны уравнением:

$a=\mu b$

Возведя обе части в квадрат, получим:

$a^{2}=b^{2}\mu ^{2}$

$a^{2}=x^{2}+y^{2}$

$b^{2}=(d-x)^{2}+y^{2}$

$x^{2}+y^{2}=[(d-x)^{2}+y^{2}]\mu ^{2}$

Расширение:

$x^{2}+y^{2}=[d^{2}+x^{2}-2dx+y^{2}]\mu ^{2}$

Дальнейшее расширение:

$x^{2}+y^{2}=x^{2}\mu ^{2}+y^{2}\mu ^{2}+d^{2}\mu ^{2}-2dx\mu ^{2}$

Переносим в левую часть:

$x^{2}-x^{2}\mu ^{2}+y^{2}-y^{2}\mu ^{2}-d^{2}\mu ^{2}+2dx\mu ^{2}=0$

Факторинг:

$x^{2}(1-\mu ^{2})+y^{2}(1-\mu ^{2})-d^{2}\mu ^{2}+2dx\mu ^{2}=0$

Деление на $1-\mu ^{2}$ :

$x^{2}+y^{2}-{\frac {d^{2}\mu ^{2}}{1-\mu ^{2}}}+{\frac {2dx\mu ^{2}}{1-\mu ^{2}}}=0$

Завершение квадрата:

$\left(x+{\frac {d\mu ^{2}}{1-\mu ^{2}}}\right)^{2}-{\frac {d^{2}\mu ^{4}}{(1-\mu ^{2})^{2}}}-{\frac {d^{2}\mu ^{2}}{1-\mu ^{2}}}+y^{2}=0$

Перенесите неквадратные члены в правую часть:

${\begin{aligned}\left(x+{\frac {d\mu ^{2}}{1-\mu ^{2}}}\right)^{2}+y^{2}&={\frac {d^{2}\mu ^{4}}{(1-\mu ^{2})^{2}}}+{\frac {d^{2}\mu ^{2}}{1-\mu ^{2}}}\\&={\frac {d^{2}\mu ^{4}}{(1-\mu ^{2})^{2}}}+{\frac {d^{2}\mu ^{2}}{1-\mu ^{2}}}{\frac {(1-\mu ^{2})}{(1-\mu ^{2})}}\\&={\frac {d^{2}\mu ^{4}+d^{2}\mu ^{2}-d^{2}\mu ^{4}}{(1-\mu ^{2})^{2}}}\\&={\frac {d^{2}\mu ^{2}}{(1-\mu ^{2})^{2}}}\end{aligned}}$

Затем:

$\left(x+{\frac {d\mu ^{2}}{1-\mu ^{2}}}\right)^{2}+y^{2}=\left({\frac {d\mu }{1-\mu ^{2}}}\right)^{2}$

Следовательно, точка должна лежать на круге, как это определено Аполлонием, а их начальные точки являются фокусами.

ось

Основная статья: Аполлонические круги

Рисунок 2. Набор аполлонических кругов. Каждый синий круг пересекает каждый красный круг под прямым углом, и наоборот. Каждый красный круг проходит через два фокуса, которые соответствуют точкам A и B на рисунке 1.

Окружности, определенные аполлонической задачей преследования для одних и тех же двух точек A и B , но с разными соотношениями двух скоростей, не пересекаются друг с другом и образуют непрерывное семейство, охватывающее всю плоскость; это семейство кругов известно как гиперболический карандаш . Другое семейство кругов, круги, проходящие через A и B , также называется карандашом или, точнее, эллиптическим карандашом . Эти два пучка аполлонических окружностей пересекают друг друга под прямым углом и составляют основу биполярной системы координат . Внутри каждого карандаша любые два круга имеют одну и ту же радикальную ось ; две радикальные оси двух карандашей перпендикулярны, а центры окружностей одного карандаша лежат на радикальной оси другого карандаша.

Решения проблемы Аполлония

Основная статья: Проблема Аполлония

Задача Аполлония может иметь до восьми решений. Три заданных кружка показаны черным цветом, а кружки решения — цветными.

В евклидовой плоской геометрии задача Аполлония состоит в том, чтобы построить окружности , касающиеся трех данных окружностей на плоскости.

Три заданных круга обычно имеют восемь различных окружностей, которые касаются к ним, и каждый круг решения включает или исключает три данных круга по-своему: в каждом решении заключено различное подмножество трех кругов.

Аполлоническая прокладка

Основная статья: Аполлоническая прокладка

Рисунок 4. Симметричная аполлоническая прокладка, также называемая насадкой Лейбница, по имени ее изобретателя Готфрида Лейбница.

Путем многократного решения задачи Аполлония по нахождению вписанного круга промежутки между взаимно касательными кругами можно заполнить сколь угодно мелко, образуя аполлонову прокладку , также известную как упаковка Лейбница или аполлонова упаковка . Эта прокладка представляет собой фрактал , самоподобный и имеющий размерность d , которая точно не известна, но равна примерно 1,3. что выше, чем у правильной (или спрямляемой ) кривой ( d = 1), но меньше, чем у плоскости ( d = 2). Аполлоническая прокладка была впервые описана Готфридом Лейбницем в 17 веке и является изогнутым предшественником треугольника Серпинского 20 века . Аполлоническая прокладка также имеет глубокие связи с другими областями математики; например, это предельное множество клейновых групп ; см. также Теорему об упаковке кругов .

Изодинамические точки треугольника

Круги Аполлония могут также обозначать три особых круга. ${\mathcal {C}}_{1},{\mathcal {C}}_{2},{\mathcal {C}}_{3}$ определяется произвольным треугольником $\mathrm {A_{1}A_{2}A_{3}}$. Круг ${\mathcal {C}}_{1}$ определяется как уникальный круг, проходящий через вершину треугольника $\mathrm {A_{1}}$ который поддерживает постоянное соотношение расстояний до двух других вершин $\mathrm {A_{2}}$ и $\mathrm {A_{3}}$ Аполлонием (ср. определение круга выше). Аналогично, круг ${\mathcal {C}}_{2}$ определяется как уникальный круг, проходящий через вершину треугольника $\mathrm {A_{2}}$ который поддерживает постоянное соотношение расстояний до двух других вершин $\mathrm {A_{1}}$ и $\mathrm {A_{3}}$и так далее по кругу ${\mathcal {C}}_{3}$.

три окружности пересекают описанную окружность треугольника . ортогонально Все Все три окружности проходят через две точки, которые называются изодинамическими точками. $S$ и $S^{\prime }$ треугольника. Линия, соединяющая эти общие точки пересечения, является радикальной осью для всех трех окружностей. Две изодинамические точки являются инверсиями друг друга относительно описанной окружности треугольника.

Центры этих трех кругов лежат на одной линии ( линии Лемуана ). Эта линия перпендикулярна радикальной оси, которая является линией, определяемой изодинамическими точками.

См. также

• точка Аполлония
• Эллипс

Библиография

• Огилви, К.С. (1990) Экскурсии по геометрии , Дувр. ISBN   0-486-26530-7 .
• Джонсон, Р.А. (1960) Расширенная евклидова геометрия , Дувр.