Аполлоническая прокладка

В математике аполлоническая прокладка или аполлонова сеть — это фрактал, созданный путем начала с тройки кругов, каждый из которых касается двух других, и последовательного заполнения большего количества кругов, каждый из которых касается еще трех. Он назван в честь греческого математика Аполлония Пергского . ^[1]

Строительство [ править ]

Построение аполлонической прокладки начинается с трех кругов. $C_{1}$ , $C_{2}$ , и $C_{3}$ (черный на рисунке), каждая из которых касается двух других, но не имеет ни одной точки тройного касания. Эти круги могут быть разных размеров, и допускается, чтобы два из них находились внутри третьего, а все три — снаружи друг друга. Как обнаружил Аполлоний, существуют еще два круга $C_{4}$ и $C_{5}$ (красные), которые касаются всех трех исходных кругов – они называются аполлоновыми кругами . Эти пять окружностей отделены друг от друга шестью изогнутыми треугольными областями, каждая из которых ограничена дугами трех попарно касающихся окружностей. Построение продолжается добавлением еще шести кругов, по одному в каждом из этих шести изогнутых треугольников, касающихся трех его сторон. Они, в свою очередь, создают еще 18 изогнутых треугольников, и построение продолжается, снова заполняя их касательными кругами, до бесконечности.

Продолжая поэтапно таким образом, конструкция добавляет $2\cdot 3^{n}$ новые круги на сцене $n$ , что дает в общей сложности $3^{n+1}+2$ круги после $n$ этапы. В пределе этот набор кругов представляет собой аполлонову прокладку. В нем каждая пара касательных окружностей имеет бесконечную цепочку окружностей Паппа , касающуюся обеих окружностей пары.

Размер каждого нового круга определяется теоремой Декарта , которая утверждает, что для любых четырех взаимно касающихся кругов радиусы $r_{i}$ кругов подчиняется уравнению

\left({\frac {1}{r_{1}}}+{\frac {1}{r_{2}}}+{\frac {1}{r_{3}}}+{\frac {1}{r_{4}}}\right)^{2}=2\left({\frac {1}{r_{1}^{2}}}+{\frac {1}{r_{2}^{2}}}+{\frac {1}{r_{3}^{2}}}+{\frac {1}{r_{4}^{2}}}\right).

Это уравнение может иметь решение с отрицательным радиусом; это означает, что один из кругов (с отрицательным радиусом) окружает три других. Одна или две исходные окружности этой конструкции или окружности, возникающие в результате этой конструкции, могут вырождаться в прямую линию, которую можно представить как окружность бесконечного радиуса. Если есть две прямые, они должны быть параллельны и считаются касающимися в бесконечной точке . Если на прокладке имеются две линии на

x

-ось и одну единицу над ней, а также окружность единичного диаметра, касательную к обеим линиям с центром на

y

-ось, затем окружности, касающиеся

x

-оси — это круги Форда , важные в теории чисел .

Аполлоническая прокладка имеет размерность Хаусдорфа около 1,3057. ^[2]^[3] Поскольку он имеет четко определенную дробную размерность, хотя он и не совсем самоподобен , его можно рассматривать как фрактал .

Симметрии [ править ]

Преобразования Мёбиуса плоскости сохраняют форму и касание окружностей и, следовательно, сохраняют структуру аполлоновой прокладки. Любые две тройки взаимно касающихся окружностей в аполлоновой прокладке могут быть отображены друг в друга с помощью преобразования Мёбиуса, а любые две аполлоновые прокладки могут быть отображены друг в друга с помощью преобразования Мёбиуса. В частности, для любых двух касательных окружностей в любой аполлоновой прокладке инверсия в окружности с центром в точке касания (частный случай преобразования Мёбиуса) превратит эти две окружности в две параллельные прямые и преобразует остальную часть прокладки в специальную форму прокладки между двумя параллельными линиями. Композиции этих инверсий можно использовать для преобразования любых двух точек касания друг в друга. Преобразования Мёбиуса также являются изометриями гиперболической плоскости , поэтому в гиперболической геометрии все аполлоновы прокладки конгруэнтны. В некотором смысле, следовательно, существует только одна аполлоническая прокладка, с точностью до (гиперболической) изометрии.

Аполлонова прокладка — это предельное множество группы преобразований Мёбиуса, известной как группа Клейна . ^[4]

В целом, для преобразований евклидовой симметрии, а не для преобразований Мёбиуса, аполлонова прокладка унаследует симметрию своего порождающего набора из трех окружностей. Однако некоторые тройки кругов могут порождать аполлоновы прокладки с более высокой симметрией, чем исходная тройка; это происходит, когда одна и та же прокладка имеет другой, более симметричный набор образующих окружностей. Особенно симметричные случаи включают аполлонову прокладку между двумя параллельными линиями (с бесконечной двугранной симметрией ), аполлонову прокладку, образованную тремя конгруэнтными кругами в равностороннем треугольнике (с симметрией треугольника), и аполлонову прокладку, образованную двумя кругами радиуса 1. окружен кругом радиуса 2 (с двумя линиями отражательной симметрии).

кругов Целочисленные упаковки аполлоновых

Целочисленная упаковка аполлоновых кругов, определяемая кривизной окружности ( −1, 2, 2, 3)
Целочисленная упаковка аполлоновых кругов, определяемая кривизной круга (−3, 5, 8, 8).
Целочисленная упаковка аполлоновых кругов, определяемая кривизной круга (−12, 25, 25, 28).
Целочисленная упаковка аполлоновых кругов, определяемая кривизной круга (−6, 10, 15, 19).
Целочисленная упаковка аполлоновых кругов, определяемая кривизной круга (−10, 18, 23, 27).

Если любые четыре взаимно касающихся круга в аполлоновой прокладке имеют целочисленную кривизну (обратную их радиусу), то все круги в прокладке будут иметь целочисленную кривизну. ^[5] Поскольку уравнение, связывающее кривизну аполлоновой прокладки, цельной или нет, имеет вид

a^{2}+b^{2}+c^{2}+d^{2}=2ab+2ac+2ad+2bc+2bd+2cd,\,

отсюда следует, что переход от одной четверки кривизн к другой можно совершать прыжками Виета , как и при нахождении нового числа Маркова . Первые несколько из этих цельных аполлонических прокладок перечислены в следующей таблице. В таблице указаны кривизны наибольших кругов прокладки. Только первые три кривизны (из пяти, показанных в таблице) необходимы для полного описания каждой прокладки – все остальные кривизны могут быть получены из этих трех.

**Интегральные аполлонические прокладки**
Начало кривизны	Симметрия
−1, 2, 2, 3, 3	D_Д2
−2, 3, 6, 7, 7	Д ₁
−3, 4, 12, 13, 13	Д ₁
−3, 5, 8, 8, 12	Д ₁
−4, 5, 20, 21, 21	Д ₁
−4, 8, 9, 9, 17	Д ₁
−5, 6, 30, 31, 31	Д ₁
−5, 7, 18, 18, 22	Д ₁
−6, 7, 42, 43, 43	Д ₁
−6, 10, 15, 19, 19	Д ₁
−6, 11, 14, 15, 23	C_С1
−7, 8, 56, 57, 57	Д ₁
−7, 9, 32, 32, 36	Д ₁
−7, 12, 17, 20, 24	C_С1
−8, 9, 72, 73, 73	Д ₁
−8, 12, 25, 25, 33	Д ₁
−8, 13, 21, 24, 28	C_С1
−9, 10, 90, 91, 91	Д ₁
−9, 11, 50, 50, 54	Д ₁
−9, 14, 26, 27, 35	C_С1
−9, 18, 19, 22, 34	C_С1
−10, 11, 110, 111, 111	Д ₁
−10, 14, 35, 39, 39	Д ₁
−10, 18, 23, 27, 35	C_С1
−11, 12, 132, 133, 133	Д ₁
−11, 13, 72, 72, 76	Д ₁
−11, 16, 36, 37, 45	C_С1
−11, 21, 24, 28, 40	C_С1
−12, 13, 156, 157, 157	Д ₁
−12, 16, 49, 49, 57	Д ₁
−12, 17, 41, 44, 48	C_С1
−12, 21, 28, 37, 37	Д ₁
−12, 21, 29, 32, 44	C_С1
−12, 25, 25, 28, 48	Д ₁
−13, 14, 182, 183, 183	Д ₁
−13, 15, 98, 98, 102	Д ₁
−13, 18, 47, 50, 54	C_С1
−13, 23, 30, 38, 42	C_С1
−14, 15, 210, 211, 211	Д ₁
−14, 18, 63, 67, 67	Д ₁
−14, 19, 54, 55, 63	C_С1
−14, 22, 39, 43, 51	C_С1
−14, 27, 31, 34, 54	C_С1
−15, 16, 240, 241, 241	Д ₁
−15, 17, 128, 128, 132	Д ₁
−15, 24, 40, 49, 49	Д ₁
−15, 24, 41, 44, 56	C_С1
−15, 28, 33, 40, 52	C_С1
−15, 32, 32, 33, 65	Д ₁

аполлоновых кругов целочисленных Перечисление упаковок

Кривизны $(a,b,c,d)$ являются корневой четверкой (наименьшей в некоторой упаковке целого круга), если $a<0\leq b\leq c\leq d$ . Они примитивны, когда $\gcd(a,b,c,d)=1$ . Определение нового набора переменных $(x,d_{1},d_{2},m)$ по матричному уравнению

{\begin{bmatrix}a\\b\\c\\d\end{bmatrix}}={\begin{bmatrix}1&0&0&0\\-1&1&0&0\\-1&0&1&0\\-1&1&1&-2\end{bmatrix}}{\begin{bmatrix}x\\d_{1}\\d_{2}\\m\end{bmatrix}}

дает систему, в которой

(a,b,c,d)

удовлетворяет уравнению Декарта именно тогда, когда

x^{2}+m^{2}=d_{1}d_{2}

. Более того,

(a,b,c,d)

примитивен именно тогда, когда

\gcd(x,d_{1},d_{2})=1

, и

(a,b,c,d)

является корневой четверкой именно тогда, когда

x<0\leq 2m\leq d_{1}\leq d_{2}

. ^[5]

Это соотношение можно использовать для поиска всех четверок примитивных корней с заданным отрицательным изгибом. $x$ . Это следует из $2m\leq d_{1}$ и $2m\leq d_{2}$ что $4m^{2}\leq d_{1}d_{2}$ , и, следовательно, это $3m^{2}\leq d_{1}d_{2}-m^{2}=x^{2}$ . Следовательно, любая корневая четверка будет удовлетворять $0\leq m\leq |x|/{\sqrt {3}}$ . Перебирая все возможные значения $m$ , $d_{1}$ , и $d_{2}$ можно найти все примитивные корневые четверки. ^[6] Следующий код Python демонстрирует этот алгоритм, создавая примитивные корневые четверки, перечисленные выше.

import math

def get_primitive_bends(n: int):
    if n == 0:
        yield 0, 0, 1, 1
        return
    for m in range(math.ceil(n / math.sqrt(3))):
        s = m**2 + n**2
        for d1 in range(max(2 * m, 1), math.floor(math.sqrt(s)) + 1):
            d2, remainder = divmod(s, d1)
            if remainder == 0 and math.gcd(n, d1, d2) == 1:
                yield -n, d1 + n, d2 + n, d1 + d2 + n - 2 * m

for n in range(15):
    for bends in get_primitive_bends(n):
        print(bends)

Кривизны, возникающие в примитивной целочисленной упаковке аполлоновых кругов, должны принадлежать набору из шести или восьми возможных классов вычетов по модулю 24, и численные данные подтверждают, что любое достаточно большое целое число из этих классов вычетов также будет присутствовать как кривизна внутри упаковки. ^[7] Эта гипотеза, известная как локально-глобальная гипотеза, оказалась ложной в 2023 году. ^[8]^[9]

Симметрия целочисленных упаковок аполлоновых кругов

Существует несколько типов двугранной симметрии , которая может возникнуть с прокладкой в зависимости от кривизны кругов.

Никакой симметрии [ править ]

Если ни одна из кривизн не повторяется в пределах первых пяти, прокладка не содержит симметрии, что представлено группой симметрии C ₁ ; примером является прокладка, описываемая кривизной (-10, 18, 23, 27).

D ₁ симметрия [ править ]

Всякий раз, когда два из пяти крупнейших кругов прокладки имеют одинаковую кривизну, эта прокладка будет иметь симметрию D ₁ , что соответствует отражению вдоль диаметра ограничивающего круга, без вращательной симметрии.

D ₂ симметрия [ править ]

Если в пределах первых пяти повторяются две разные кривизны, прокладка будет иметь _D2 симметрию ; такая симметрия состоит из двух отражений (перпендикулярных друг другу) вдоль диаметров ограничивающего круга с двойной вращательной симметрией 180 °. Прокладка, описываемая кривизной (-1, 2, 2, 3), является единственной аполлоновой прокладкой (с точностью до масштабного коэффициента), обладающей _{D 2} симметрией .

D ₃ симметрия [ править ]

не существует Целочисленных прокладок с симметрией D ₃ .

Если три круга с наименьшей положительной кривизной имеют одинаковую кривизну, прокладка будет иметь симметрию D ₃ , что соответствует трем отражениям вдоль диаметров ограничивающего круга (на расстоянии 120 ° друг от друга), а также тройную вращательную симметрию 120 °. В этом случае отношение кривизны ограничивающего круга к трем внутренним кругам составляет 2 √ 3 - 3. Поскольку это соотношение нерационально, никакие целые упаковки аполлоновых кругов не обладают этой симметрией D ₃ , хотя многие упаковки близки к этому.

Почти D ₃ симметрия -

собой цельную аполлонову прокладку, имеющую симметрию D3 _{Фигура слева представляет} . Тот же рисунок показан справа, с метками, обозначающими кривизну внутренних кругов, иллюстрируя, что прокладка на самом деле обладает только симметрией D _1, общей для многих других цельных аполлонических прокладок.

В следующей таблице перечислено больше таких почти цельных аполлонических прокладок D ₃ . Последовательность обладает некоторыми интересными свойствами, и в таблице приведена факторизация кривизн, а также множитель, необходимый для перехода от предыдущего набора к текущему. Абсолютные значения кривизн дисков «а» подчиняются рекуррентному соотношению $a (n) = 4 a (n -1)-a (n - 2)$ (последовательность A001353 в ОЭИС ), из которого следует, что множитель сходится к √ 3 + 2 ≈ 3,732050807.

**Интегральные аполлоновы прокладки с *близкой к D3* _. симметрией,**
Кривизна				Факторы			Множитель
а	б	с	д	а	б	д	а	б	с	д
−1	2	2	3	1×1	1×2	1×3	—	—	—	—
−4	8	9	9	2×2	2×4	3×3	4.000000000	4.000000000	4.500000000	3.000000000
−15	32	32	33	3×5	4×8	3×11	3.750000000	4.000000000	3.555555556	3.666666667
−56	120	121	121	8×7	8×15	11×11	3.733333333	3.750000000	3.781250000	3.666666667
−209	450	450	451	11×19	15×30	11×41	3.732142857	3.750000000	3.719008264	3.727272727
−780	1680	1681	1681	30×26	30×56	41×41	3.732057416	3.733333333	3.735555556	3.727272727
−2911	6272	6272	6273	41×71	56×112	41×153	3.732051282	3.733333333	3.731112433	3.731707317
−10864	23408	23409	23409	112×97	112×209	153×153	3.732050842	3.732142857	3.732302296	3.731707317
−40545	87362	87362	87363	153×265	209×418	153×571	3.732050810	3.732142857	3.731983425	3.732026144

Последовательные кривизны [ править ]

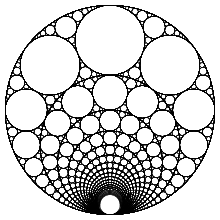
Для любого целого числа n > 0 существует аполлонова прокладка, определяемая следующими кривизнами:
(− n , n + 1, n ( n + 1), n ( n + 1) + 1).
Например, прокладки, определенные как (-2, 3, 6, 7), (-3, 4, 12, 13), (-8, 9, 72, 73) и (-9, 10, 90, 91 ) все следуют этому шаблону. Поскольку каждая внутренняя окружность, определяемая n + 1, может стать ограничивающей окружностью (определяемой − n ) в другой прокладке, эти прокладки могут быть вложенными . Это показано на рисунке справа, где показаны эти последовательные прокладки с n от 2 до 20.

См. также [ править ]

Аполлоническая сеть — граф, полученный из конечных подмножеств аполлоновой прокладки.
Упаковка аполлонической сферы , трехмерное обобщение аполлонической прокладки.
Треугольник Серпинского — самоподобный фрактал с похожей комбинаторной структурой.

Примечания [ править ]

^ Сатия, II, Бабочка в мире Иглесиаса Васеаса: история самого увлекательного квантового фрактала ( Бристоль : IOP Publishing , 2016), стр. 5 .
^ Бойд, Дэвид В. (1973), «Остаточная размерность аполлоновой упаковки», Mathematika , 20 (2): 170–174, doi : 10.1112/S0025579300004745 , MR 0493763
^ Макмаллен, Кертис Т. (1998), «Хаусдорфовая размерность и конформная динамика, III: Вычисление размерности» (PDF) , American Journal of Mathematics , 120 (4): 691–721, doi : 10.1353/ajm.1998.0031 , MR 1637951 , S2CID 15928775
^ Счет кругов и эргодическая теория клейнианских групп Хи О Брауна. Университет, декабрь 2009 г.
^ Jump up to: Перейти обратно: ^а ^б Рональд Л. Грэм, Джеффри К. Лагариас, Колин М. Мэллоуз, Алан Р. Уилкс и Кэтрин Х. Ян; «Упаковки аполлоновых кругов: теория чисел» Дж. Теория чисел, 100 (2003), 1–45.
^ Брэдфорд, Олден. «Возвращение к аполлоническим прокладкам» . Проверено 7 августа 2022 г.
^ Фукс, Елена; Санден, Кэтрин (28 ноября 2011 г.). «Некоторые эксперименты с целыми упаковками аполлоновых кругов». Экспериментальная математика . 20 (4): 380–399. arXiv : 1001.1406 . дои : 10.1080/10586458.2011.565255 . ISSN 1058-6458 .
^ Саммер Хааг; Клайд Кертцер; Джеймс Рикардс; Кэтрин Э. Стэндж. «Локально-глобальная гипотеза об упаковках аполлоновых кругов неверна». arXiv : 2307.02749 .
^ Леви, Макс Г. (10 августа 2023 г.). «Два студента разгадывают широко распространенную математическую гипотезу» . Журнал Кванта . Проверено 14 августа 2023 г.

Ссылки [ править ]

Бенуа Б. Мандельброт: Фрактальная геометрия природы , WH Freeman, 1982, ISBN 0-7167-1186-9
Пол Д. Бурк: « Введение во фрактал Аполлонии ». Компьютеры и графика, том 30, выпуск 1, январь 2006 г., страницы 134–136.
Дэвид Мамфорд , Серия Кэролайн , Дэвид Райт: Жемчуг Индры: видение Феликса Кляйна , издательство Кембриджского университета, 2002, ISBN 0-521-35253-3
Джеффри К. Лагариас, Колин Л. Мэллоуз, Аллан Р. Уилкс: За пределами теоремы о круге Декарта , The American Mathematical Monthly, Vol. 109, № 4 (апрель 2002 г.), стр. 338–361, ( arXiv:math.MG/0101066 v1, 9 января 2001 г. )

Внешние ссылки [ править ]

Вайсштейн, Эрик В. «Аполлоническая прокладка» . Математический мир .
Александр Богомольный , Аполлоническая прокладка , разрезание узла
Интерактивная аполлоническая прокладка, работающая на чистом HTML5 на Wayback Machine (архивировано 2 мая 2011 г.)
Сценарий Matlab для построения 2D-аполлонической прокладки с n одинаковыми кругами. Архивировано 7 октября 2008 г. в Wayback Machine с использованием инверсии кругов.
Онлайн-эксперименты с JSXGraph
Аполлоническая прокладка Майкла Скрайбера, Демонстрационный проект Вольфрама .
Интерактивная аполлоническая прокладка Демонстрация аполлоновой прокладки, работающей на Java
Дана Маккензи. Информатика: Тискет, Таскет, Аполлоническая прокладка . Американский ученый, январь/февраль 2010 г.
«Рисование песком крупнейшего в мире произведения искусства» , The Telegraph , 16 декабря 2009 г. Газетная статья о произведении искусства в виде частичной аполлонической прокладки с внешней окружностью девять миль.
Динамические аполлонические прокладки , Тартапелаг Джорджио Пьетроколы, 2014 г. (на итальянском языке)

[1] Сатия, II, Бабочка в мире Иглесиаса Васеаса: история самого увлекательного квантового фрактала ( Бристоль : IOP Publishing , 2016), стр. 5 .

[2] Бойд, Дэвид В. (1973), «Остаточная размерность аполлоновой упаковки», Mathematika , 20 (2): 170–174, doi : 10.1112/S0025579300004745 , MR 0493763

[3] Макмаллен, Кертис Т. (1998), «Хаусдорфовая размерность и конформная динамика, III: Вычисление размерности» (PDF) , American Journal of Mathematics , 120 (4): 691–721, doi : 10.1353/ajm.1998.0031 , MR 1637951 , S2CID 15928775

[4] Счет кругов и эргодическая теория клейнианских групп Хи О Брауна. Университет, декабрь 2009 г.

[Graham_et_al-5] Jump up to: Перейти обратно: ^а ^б Рональд Л. Грэм, Джеффри К. Лагариас, Колин М. Мэллоуз, Алан Р. Уилкс и Кэтрин Х. Ян; «Упаковки аполлоновых кругов: теория чисел» Дж. Теория чисел, 100 (2003), 1–45.

[6] Брэдфорд, Олден. «Возвращение к аполлоническим прокладкам» . Проверено 7 августа 2022 г.

[7] Фукс, Елена; Санден, Кэтрин (28 ноября 2011 г.). «Некоторые эксперименты с целыми упаковками аполлоновых кругов». Экспериментальная математика . 20 (4): 380–399. arXiv : 1001.1406 . дои : 10.1080/10586458.2011.565255 . ISSN 1058-6458 .

[8] Саммер Хааг; Клайд Кертцер; Джеймс Рикардс; Кэтрин Э. Стэндж. «Локально-глобальная гипотеза об упаковках аполлоновых кругов неверна». arXiv : 2307.02749 .

[9] Леви, Макс Г. (10 августа 2023 г.). «Два студента разгадывают широко распространенную математическую гипотезу» . Журнал Кванта . Проверено 14 августа 2023 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

v т и Проблемы с упаковкой
Abstract packing	Bin Set
Circle packing	In a circle / equilateral triangle / isosceles right triangle / square Apollonian gasket Circle packing theorem Tammes problem (on sphere)
Sphere packing	Apollonian Finite In a sphere In a cube In a cylinder Close-packing Kissing number Sphere-packing (Hamming) bound
Other 2-D packing	Square packing
Other 3-D packing	Tetrahedron Ellipsoid
Puzzles	Conway Slothouber–Graatsma

v т и Фракталы
Characteristics	Fractal dimensions Assouad Box-counting Higuchi Correlation Hausdorff Packing Topological Recursion Self-similarity
Iterated function system	Barnsley fern Cantor set Koch snowflake Menger sponge Sierpinski carpet Sierpinski triangle Apollonian gasket Fibonacci word Space-filling curve Blancmange curve De Rham curve Minkowski Dragon curve Hilbert curve Koch curve Lévy C curve Moore curve Peano curve Sierpiński curve Z-order curve String T-square n-flake Vicsek fractal Hexaflake Gosper curve Pythagoras tree Weierstrass function
Strange attractor	Multifractal system
L-system	Fractal canopy Space-filling curve H tree
Escape-time fractals	Burning Ship fractal Julia set Filled Newton fractal Douady rabbit Lyapunov fractal Mandelbrot set Misiurewicz point Multibrot set Newton fractal Tricorn Mandelbox Mandelbulb
Rendering techniques	Buddhabrot Orbit trap Pickover stalk
Random fractals	Brownian motion Brownian tree Brownian motor Fractal landscape Lévy flight Percolation theory Self-avoiding walk
People	Michael Barnsley Georg Cantor Bill Gosper Felix Hausdorff Desmond Paul Henry Gaston Julia Helge von Koch Paul Lévy Aleksandr Lyapunov Benoit Mandelbrot Hamid Naderi Yeganeh Lewis Fry Richardson Wacław Sierpiński
Other	"How Long Is the Coast of Britain?" Coastline paradox Fractal art List of fractals by Hausdorff dimension The Fractal Geometry of Nature (1982 book) The Beauty of Fractals (1986 book) Chaos: Making a New Science (1987 book) Kaleidoscope Chaos theory