Игра Хаос
В математике термин «игра хаоса» первоначально относился к методу создания фрактала с использованием многоугольника и случайной начальной точки внутри него. [1] [2] Фрактал создается путем итеративного создания последовательности точек, начиная с начальной случайной точки, в которой каждая точка последовательности представляет собой заданную долю расстояния между предыдущей точкой и одной из вершин многоугольника; вершина выбирается случайным образом на каждой итерации. Повторение этого итерационного процесса большое количество раз, случайный выбор вершины на каждой итерации и удаление первых нескольких точек последовательности часто (но не всегда) приводит к образованию фрактальной формы. Использование правильного треугольника и коэффициента 1/2 приведет к образованию треугольника Серпинского , а создание правильного расположения с четырьмя точками и коэффициентом 1/2 создаст отображение «Тетраэдра Серпинского», трехмерного аналога Серпинского. треугольник. Когда количество точек увеличивается до числа N, расположение образует соответствующий (N-1)-мерный симплекс Серпинского .
Этот термин был обобщен для обозначения метода создания аттрактора или фиксированной точки любой системы итерированных функций (IFS). Начиная с любой точки x 0 , последовательные итерации формируются как x k+1 = f r (x k ), где f r — член заданной IFS, случайно выбираемый для каждой итерации. Итерации сходятся к фиксированной точке IFS. Всякий раз, когда x 0 принадлежит аттрактору IFS, все итерации x k остаются внутри аттрактора и с вероятностью 1 образуют плотное множество в последнем .
Метод «игры хаоса» отображает точки в случайном порядке по всему аттрактору. В этом отличие от других методов рисования фракталов, которые проверяют каждый пиксель на экране, чтобы определить, принадлежит ли он фракталу. Общую форму фрактала можно быстро построить с помощью метода «игры хаоса», но детальное изображение некоторых областей фрактала может оказаться затруднительным.
С помощью «игры хаоса» можно создать новый фрактал и при создании нового фрактала получить некоторые параметры. Эти параметры полезны для приложений теории фракталов, таких как классификация и идентификация. [3] [4] Новый фрактал подобен оригиналу по некоторым важным характеристикам, таким как фрактальная размерность.
Оптимальное значение r для каждого правильного многоугольника [ править ]
На каждой итерации игры в хаос точка x k+1 может быть размещена в любом месте на линии, соединяющей точку x k и выбранную вершину v. Определив r как отношение между двумя расстояниями d(x k , x k +1 ) и d(x k ,v), можно найти оптимальное значение r, т. е. r opt , для каждого N-стороннего правильного многоугольника, который создает фрактал с оптимальной упаковкой, т. е. подмасштабные многоугольники имеют вид соприкасаются, но не перекрываются.
Значение r opt можно рассчитать как отношение длины стороны первого многоугольника подмасштаба к стороне исходного многоугольника. Это соотношение можно рассчитать геометрически: [5]
В котором а рассчитывается как:
![{\displaystyle a=\sum _{i=1}^{n}\cos[i(\pi -\theta)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/989ab39354ef3bbf598991180bf09ef434dcc9de)
Где θ – внутренний угол многоугольника, а n – индекс наиболее выступающей вершины, отсчитываемый от основания, т.е. где представляет собой целую часть дроби.
Пятиугольник (r=0,618)
Шестиугольник (r=0,667)
Семиугольник (r=0,692)
Восьмиугольник (r=0,707)
Нонагон (r=0,742)
Декагон (r=0,764)
Расширение игры хаоса для значений r больше 1 [ править ]
Хотя оптимально упакованный фрактал появляется только при определенном значении r, т. е. r opt , в игру хаоса можно играть и с использованием других значений. Если r>1 (точка x k+1 прыгает на большее расстояние, чем расстояние между точкой x k и вершиной v), то сгенерированная фигура выходит за пределы исходного многоугольника. [5] Когда r=2, алгоритм переходит в метастабильное состояние и генерирует квазисимметричные фигуры. При значениях r>2 на каждой итерации точки размещаются все дальше и дальше от центра исходного многоугольника, алгоритм становится неустойчивым и фигура не генерируется.
г=1,4
г=1,6
г=2
г=2,1
Ограниченная игра хаоса [ править ]
Если игра в хаос проводится с квадратом, фрактал не появляется, и внутренняя часть квадрата равномерно заполняется точками. Однако если на выбор вершин наложить ограничения, в квадрате появятся фракталы. Например, если текущую вершину невозможно выбрать на следующей итерации, появляется такой фрактал:
Если текущая вершина не может находиться на расстоянии одного места (против часовой стрелки) от ранее выбранной вершины, появляется этот фрактал:
Если не дать точке приземлиться на определенную область квадрата, форма этой области будет воспроизведена как фрактал в других и, по-видимому, неограниченных частях квадрата.
Точка внутри квадрата неоднократно прыгает на половину расстояния в сторону случайно выбранной вершины, но выбранная в данный момент вершина не может находиться на расстоянии 2 позиций от ранее выбранной вершины.
Точка внутри квадрата неоднократно прыгает на половину расстояния к случайно выбранной вершине, но выбранная в данный момент вершина не может соседствовать с ранее выбранной вершиной, если две ранее выбранные вершины одинаковы.
Точка внутри пятиугольника неоднократно прыгает на половину расстояния в сторону случайно выбранной вершины, но выбранная в данный момент вершина не может совпадать с ранее выбранной вершиной.
Точка внутри пятиугольника неоднократно прыгает на половину расстояния в сторону случайно выбранной вершины, но выбранная в данный момент вершина не может соседствовать с ранее выбранной вершиной, если две ранее выбранные вершины одинаковы.
Прыжки, отличные от 1/2 [ править ]
Когда длина прыжка к вершине или другой точке не равна 1/2, игра хаоса порождает другие фракталы, некоторые из них очень хорошо известны. Например, когда прыжок равен 2/3 и точка также может прыгнуть к центру квадрата, игра хаоса генерирует фрактал Вичека :
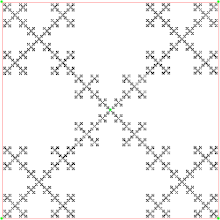
Когда прыжок равен 2/3 и точка также может прыгать к середины четырех сторон, игра хаоса генерирует ковер Серпинского :
используемая для представления последовательностей , Игра хаоса
С небольшими изменениями в правилах игры можно использовать алгоритм игры хаоса для представления любой четко определенной последовательности , т. е. последовательности, состоящей из повторения ограниченного числа различных элементов. Фактически, для последовательности с числом N различных элементов можно сыграть в игру хаоса на N-стороннем многоугольнике, назначая каждый элемент вершине и играя в игру, выбирая вершины в соответствии с развитием последовательности (вместо этого выбора случайной вершины). В этой версии игры сгенерированное изображение является уникальным представлением последовательности. Этот метод был применен к представлению генов (N=4, r=0,5). [6] [7] и белки (N=20, r=0,863). [5] [8] Кроме того, представления белковых последовательностей использовались для указания моделям ML предсказывать свойства белков. [5] [9] Расширение игры хаоса с использованием r=2 может быть полезно для увеличения небольших мутаций при сравнении двух (или более) последовательностей. [5]
г=0,5
г=2
См. также [ править ]
Внешние ссылки [ править ]
- Моделирование игр хаоса, созданное с помощью Scratch .
- Объяснение игры хаоса на сайте Beltoforion.de.
Ссылки [ править ]
- ^ Вайсштейн, Эрик В. «Игра Хаоса» . Математический мир .
- ^ Барнсли, Майкл (1993). Фракталы повсюду . Морган Кауфманн . ISBN 978-0-12-079061-6 .
- ^ Джампур, Махди; Ягуби, Махди; Ашурзаде, Марьям; Сулеймани, Адель (1 сентября 2010 г.). «Новый быстрый метод идентификации отпечатков пальцев с использованием теории фракталов и игр хаоса» . Фракталы . 18 (3): 293–300. дои : 10.1142/s0218348x10005020 . ISSN 0218-348X – через ResearchGate .
- ^ Джампур, Махди; Джавиди, Мохаммед М.; Сулеймани, Адель; Ашурзаде, Марьям; Ягуби, Махди (2010). «Новый метод сохранения отпечатков пальцев на малой громкости с использованием игры хаоса и теории фракталов» . Международный журнал интерактивных мультимедиа и искусственного интеллекта . 1 (3): 27. дои : 10.9781/ijimai.2010.135 . ISSN 1989-1660 .
- ↑ Перейти обратно: Перейти обратно: а б с д и Арсиччо, Андреа; Стратта, Лоренцо; Мензен, Тим (15 ноября 2023 г.). «Оценка представления белков в хаос-игре для применения в моделях машинного обучения: прогнозирование сродства и специфичности антител на примере тематического исследования» . Журнал молекулярного моделирования . 29 (12): 377. doi : 10.1007/s00894-023-05777-0 . ISSN 0948-5023 .
- ^ Джеффри HJ (1990) «Хаос-игровое представление структуры генов». Нуклеиновые кислоты Res 18(8): 2163–2170. https://doi.org/10.1093/nar/18.8.2163
- ^ Джеффри, Х. Джоэл (1 января 1992 г.). «Хаос-игровая визуализация последовательностей» . Компьютеры и графика . 16 (1): 25–33. дои : 10.1016/0097-8493(92)90067-6 . ISSN 0097-8493 .
- ^ Алмейда, Йонас С.; Винга, Сусана (31 марта 2009 г.). «Биологические последовательности как изображения – общее двумерное решение для повторяющихся карт» . БМК Биоинформатика . 10 (1): 100. дои : 10.1186/1471-2105-10-100 . ISSN 1471-2105 . ПМК 2678093 . ПМИД 19335894 .
- ^ Чжоу, Цянь; Ци, Сайбин; Рен, Конг (01 марта 2021 г.). «Прогнозирование существенности генов на основе представления игры хаоса и импульсных нейронных сетей» . Хаос, солитоны и фракталы . 144 : 110649. дои : 10.1016/j.chaos.2021.110649 . ISSN 0960-0779 .