Самоподобие


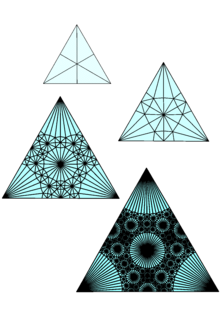
В математике объект самоподобный точно или приблизительно подобен своей части (т. е. целое имеет ту же форму, что и одна или несколько частей). Многие объекты в реальном мире, такие как береговые линии , статистически самоподобны: части из них демонстрируют одинаковые статистические свойства во многих масштабах. [2] Самоподобие — типичное свойство фракталов . Масштабная инвариантность — это точная форма самоподобия, при которой при любом увеличении остается меньшая часть объекта, похожая на целое. Например, сторона снежинки Коха одновременно симметрична и масштабно-инвариантна; его можно постоянно увеличивать в 3 раза без изменения формы. Нетривиальное сходство, проявляющееся во фракталах, отличается их тонкой структурой или детализацией в сколь угодно малых масштабах. В качестве контрпримера , хотя любая часть прямой линии может напоминать целое, дальнейшие детали не раскрываются.
Говорят, что развивающееся во времени явление демонстрирует самоподобие, если числовое значение некоторой наблюдаемой величины измеренные в разное время, различны, но соответствующая безразмерная величина при данном значении остаются инвариантными. Это происходит, если количество демонстрирует динамическое масштабирование . Идея является лишь развитием идеи подобия двух треугольников. [3] [4] [5] Обратите внимание, что два треугольника подобны, если численные значения их сторон различны, однако соответствующие безразмерные величины, например углы, совпадают.
Пейтген и др. объясните это понятие как таковое:
Если части фигуры являются маленькими копиями целого, то фигура называется самоподобной .... Фигура является строго самоподобной , если ее можно разложить на части, являющиеся точными копиями целого. Любая произвольная часть содержит точную копию всей фигуры. [6]
Поскольку математически фрактал может проявлять самоподобие при неограниченном увеличении, воссоздать это физически невозможно. Пейтген и др. предложить изучать самоподобие с помощью приближений:
Чтобы придать операциональный смысл свойству самоподобия, мы неизбежно ограничиваемся конечными приближениями предельной фигуры. Это делается с помощью метода, который мы назовем коробочным самоподобием, при котором измерения производятся на конечных этапах фигуры с использованием сеток различных размеров. [7]
Этот словарь был введен Бенуа Мандельбротом в 1964 году. [8]
Самородство [ править ]

В математике части самоаффинность — это свойство фрактала , которого масштабируются на разную величину в направлениях x и y. Это означает, что для того, чтобы оценить самоподобие этих фрактальных объектов, их необходимо масштабировать с помощью анизотропного аффинного преобразования .
Определение [ править ]
Компактное конечное топологическое пространство X называется самоподобным, если существует множество S, индексирующее множество несюръективных гомеоморфизмов . для чего
Если , мы называем X самоподобным, если это единственное такое , что непустое подмножество Y приведенное выше уравнение справедливо для . Мы звоним
структура самоподобная . Гомеоморфизмы могут быть повторены , что приводит к повторной системе функций . Композиция функций создает алгебраическую структуру моноида . Когда множество S состоит только из двух элементов, моноид известен как диадический моноид . Диадический моноид можно представить как бесконечное двоичное дерево ; в более общем смысле, если множество S имеет p элементов, то моноид можно представить как p-адическое дерево.
Автоморфизмы ; диадического моноида — группа модулярная автоморфизмы можно представить как гиперболические вращения бинарного дерева.
Более общим понятием, чем самоподобие, является Самоподобие .
Примеры [ править ]


Множество Мандельброта также самоподобно относительно точек Мисюревича .
Самоподобие имеет важные последствия для проектирования компьютерных сетей, поскольку типичный сетевой трафик имеет свойства самоподобия. Например, в инженерии телетрафика модели трафика данных с коммутацией пакетов кажутся статистически самоподобными. [9] Это свойство означает, что простые модели, использующие распределение Пуассона, являются неточными, а сети, спроектированные без учета самоподобия, скорее всего, будут функционировать неожиданным образом.
Аналогичным образом, движения фондового рынка описываются как демонстрирующие самоподобие , т.е. они кажутся самоподобными при преобразовании с помощью соответствующего аффинного преобразования для отображаемого уровня детализации. [10] Эндрю Ло описывает самоподобие логарифма доходности фондового рынка в эконометрике . [11]
Правила конечного подразделения — мощный метод построения самоподобных множеств, включая множество Кантора и треугольник Серпинского .
В кибернетике [ править ]
Модель жизнеспособной системы Стаффорда Бира представляет собой организационную модель с аффинной самоподобной иерархией, в которой данная жизнеспособная система является одним элементом Системы Один из жизнеспособной системы на один рекурсивный уровень выше, и для которой элементы ее Системы Один являются жизнеспособными системами на один рекурсивный уровень ниже.
В природе [ править ]

Самоподобие можно найти и в природе. Справа — математически созданное, совершенно самоподобное изображение папоротника , которое имеет заметное сходство с естественными папоротниками. Другие растения, такие как брокколи романеско , демонстрируют сильное самоподобие.
В музыке [ править ]
- Строгие каноны демонстрируют различные типы и степени самоподобия, как и разделы фуг .
- Тон Шепарда самоподобен в области частот и длин волн.
- Датский названную композитор Пер Норгорд использовал самоподобную целочисленную последовательность, «бесконечный ряд», в большей части своей музыки.
- В области поиска музыкальной информации самоподобие обычно означает тот факт, что музыка часто состоит из частей, которые повторяются во времени. [12] Другими словами, музыка самоподобна при временном переводе, а не при масштабировании (или в дополнение к нему). [13]
См. также [ править ]
Ссылки [ править ]
- ^ Мандельброт, Бенуа Б. (1982). Фрактальная геометрия природы , стр.44. ISBN 978-0716711865 .
- ^ Мандельброт, Бенуа Б. (5 мая 1967 г.). «Какой длины побережье Британии? Статистическое самоподобие и дробная размерность» . Наука . Новая серия. 156 (3775): 636–638. Бибкод : 1967Sci...156..636M . дои : 10.1126/science.156.3775.636 . ПМИД 17837158 . S2CID 15662830 . PDF
- ^ Хасан МК, Хасан МЗ, Павел Н.И. (2011). «Динамическое масштабирование, схлопывание данных и самоподобие в сетях Барабаси-Альберта». Дж. Физ. А: Математика. Теор . 44 (17): 175101. arXiv : 1101.4730 . Бибкод : 2011JPhA...44q5101K . дои : 10.1088/1751-8113/44/17/175101 . S2CID 15700641 .
{{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка ) - ^ Хасан МК, Хасан МЗ (2009). «Появление фрактального поведения в агрегации, вызванной конденсацией». Физ. Преподобный Е. 79 (2): 021406. arXiv : 0901.2761 . Бибкод : 2009PhRvE..79b1406H . дои : 10.1103/physreve.79.021406 . ПМИД 19391746 . S2CID 26023004 .
- ^ Дайин Ф.Р., Хасан М.К. (2016). «Мульти-мультифрактальность, динамическое масштабирование и статистика окрестности во взвешенной плоской стохастической решетке». Хаос, солитоны и фракталы . 91 : 228. arXiv : 1409.7928 . Бибкод : 2016CSF....91..228D . дои : 10.1016/j.chaos.2016.06.006 .
- ^ Пейтген, Хайнц-Отто; Юргенс, Хартмут; Саупе, Дитмар; Малецкий, Эван; Персианте, Терри; и Юнкер, Ли (1991). Фракталы для класса: Стратегическая деятельность, том первый , стр.21. Спрингер-Верлаг, Нью-Йорк. ISBN 0-387-97346-X и ISBN 3-540-97346-X .
- ^ Пейтген и др. (1991), стр.2-3.
- ^ Как я открыл фракталы, Интервью с Бенуа Мандельбротом , La Recherche https://www.larecherche.fr/math%C3%A9matiques-histoire-des-sciences/%C2%AB-comment-jai-d%C3 %A9covered- фракталы-%C2%BB
- ^ Лиланд, МЫ; Такку, М.С.; и др. (январь 1995 г.). «О самоподобной природе трафика Ethernet (расширенная версия)» (PDF) . Транзакции IEEE/ACM в сети . 2 (1): 1–15. дои : 10.1109/90.282603 . S2CID 6011907 .
- ^ Бенуа Мандельброт (февраль 1999 г.). «Как фракталы могут объяснить, что не так с Уолл-стрит» . Научный американец .
- ^ Кэмпбелл, Ло и МакКинли (1991) « Эконометрика финансовых рынков», Princeton University Press! ISBN 978-0691043012
- ^ Фут, Джонатан (30 октября 1999 г.). «Визуализация музыки и звука с использованием самоподобия». Материалы седьмой международной конференции ACM по мультимедиа (Часть 1) (PDF) . стр. 77–80. CiteSeerX 10.1.1.223.194 . дои : 10.1145/319463.319472 . ISBN 978-1581131512 . S2CID 3329298 . Архивировано (PDF) из оригинала 9 августа 2017 года.
- ^ Парейон, Габриэль (апрель 2011 г.). О музыкальном самоподобии: интерсемиоз как синекдоха и аналогия (PDF) . Международный институт семиотики в Иматре; Семиотическое общество Финляндии. п. 240. ИСБН 978-952-5431-32-2 . Архивировано из оригинала (PDF) 8 февраля 2017 года . Проверено 30 июля 2018 г. (Также см. Google Книги )
Внешние ссылки [ править ]
- «Медные шевроны» — самоподобный фрактальный зум-фильм.
- «Самоподобие» — Новые статьи о самоподобии. Алгоритм вальса
Самородство [ править ]
- Мандельброт, Бенуа Б. (1985). «Самосродство и фрактальное измерение» (PDF) . Физика Скрипта . 32 (4): 257–260. Бибкод : 1985PhyS...32..257M . дои : 10.1088/0031-8949/32/4/001 . S2CID 250815596 .
- Сапожников, Виктор; Фуфула-Джорджиу, Эфи (май 1996 г.). «Самосродство в разветвленных реках» (PDF) . Исследования водных ресурсов . 32 (5): 1429–1439. Бибкод : 1996WRR....32.1429S . дои : 10.1029/96wr00490 . Архивировано (PDF) из оригинала 30 июля 2018 года . Проверено 30 июля 2018 г.
- Бенуа Б. Мандельброт (2002). Гауссово самоаффинность и фракталы: глобальность, Земля, шум 1/F и R/S . Спрингер. ISBN 978-0387989938 .





