Автоморфизм

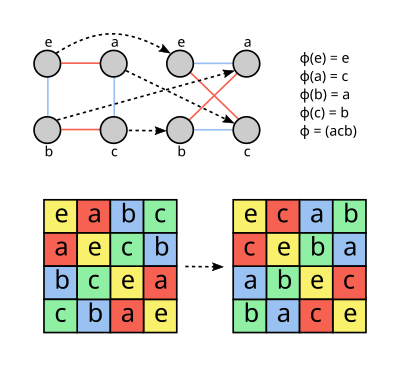
В математике автоморфизм — это изоморфизм математического объекта самому себе. В каком-то смысле это симметрия объекта и способ отображения объекта на самого себя с сохранением всей его структуры. Совокупность всех автоморфизмов объекта образует группу , называемую группой автоморфизмов . Грубо говоря, это группа симметрии объекта.

Определение [ править ]

В алгебраической структуре, такой как группа , кольцо или векторное пространство , автоморфизм — это просто биективный гомоморфизм объекта в самого себя. (Определение гомоморфизма зависит от типа алгебраической структуры; см., например, групповой гомоморфизм , кольцевой гомоморфизм и линейный оператор .)

В более общем смысле, для объекта в некоторой категории автоморфизм — это морфизм объекта на самого себя, который имеет обратный морфизм; то есть морфизм $f:X\to X$ является автоморфизмом, если существует морфизм $g:X\to X$ такой, что $g\circ f=f\circ g=\operatorname {id} _{X},$ где $\operatorname {id} _{X}$ является морфизмом X $.$ тождественным Для алгебраических структур эти два определения эквивалентны; в этом случае тождественный морфизм представляет собой просто тождественную функцию и часто называется тривиальным автоморфизмом

Группа автоморфизмов [ править ]

Автоморфизмы объекта $X$ образуют группу по композиции морфизмов , называется группой X. $которая$ автоморфизмов Это следует непосредственно из определения категории.

Группу автоморфизмов объекта $X$ в категории $C$ часто обозначают $Aut C (X)$ или просто Aut( X ), если категория ясна из контекста.

Примеры [ править ]

В теории множеств произвольная перестановка элементов множества X является автоморфизмом. Группу автоморфизмов X также называют симметрической группой на X .
В элементарной арифметике множество целых чисел Z , рассматриваемое как сложенная группа, имеет уникальный нетривиальный автоморфизм: отрицание. Однако, рассматриваемое как кольцо, оно обладает лишь тривиальным автоморфизмом. Вообще говоря, отрицание — это автоморфизм любой абелевой группы , но не кольца или поля.
Групповой автоморфизм — это групповой изоморфизм группы в себя. Неформально это такая перестановка элементов группы, при которой структура остается неизменной. Для каждой группы G существует естественный групповой гомоморфизм G → Aut( G ), образ которого группа Inn( G ) внутренних автоморфизмов и ядро является центром G. есть которого Таким образом, если G имеет тривиальный центр, ее можно вложить в собственную группу автоморфизмов. ^[1]
В линейной алгебре векторного пространства V является линейный оператор V → V. эндоморфизмом Автоморфизм — это обратимый линейный оператор на V . Когда векторное пространство конечномерно, группа автоморфизмов V совпадает с общей линейной группой GL( V ). (Алгебраическая структура всех эндоморфизмов V сама по себе является алгеброй над тем же базовым полем, что и V которой , обратимые элементы в точности состоят из GL( V ).)
Полевой автоморфизм — это биективный гомоморфизм колец поля в себя.
- Поле $\mathbb {Q}$ рациональных чисел не имеет другого автоморфизма, кроме тождества, поскольку автоморфизм должен фиксировать аддитивное тождество $0$ и мультипликативное тождество $1$ ; сумма конечного числа $1$ должна быть фиксированной, а также аддитивные обратные к этим суммам (т. е. автоморфизм фиксирует все целые числа ); наконец, поскольку каждое рациональное число является частным двух целых чисел, все рациональные числа должны быть зафиксированы любым автоморфизмом.
- Поле $\mathbb {R}$ действительных чисел не имеет другого автоморфизма, кроме тождества. Действительно, рациональные числа должны быть зафиксированы каждым автоморфизмом, как указано выше; автоморфизм должен сохранять неравенства, поскольку $x<y$ эквивалентно $\exists z\mid y-x=z^{2},$ и последнее свойство сохраняется при любом автоморфизме; наконец, каждое действительное число должно быть фиксировано, поскольку оно является наименьшей верхней границей последовательности рациональных чисел.
- Поле $\mathbb {C}$ комплексных чисел имеет уникальный нетривиальный автоморфизм, который отправляет $\mathbb {R}$ в $\mathbb {R} ,$ комплексное сопряжение , но существует бесконечно ( несчетно ) множество «диких» автоморфизмов, если аксиому выбора . принять ^[2]^[3]
- Исследование автоморфизмов расширений алгебраических полей — отправная точка и главный объект теории Галуа .
Группа автоморфизмов кватернионов ( H ) как кольцо - это внутренние автоморфизмы по теореме Скулема – Нётер : отображения вида a ↦ bab ⁻¹. ^[4] Эта группа изоморфна SO (3) — группе вращений в трёхмерном пространстве.
Группа автоморфизмов октонионов ( O ) — это исключительная группа G2 _Ли .
В теории графов автоморфизм графа — это перестановка узлов, сохраняющая ребра и неребра. В частности, если два узла соединены ребром, то же самое относится и к их изображениям при перестановке.
В геометрии автоморфизм можно назвать движением пространства. Также используется специализированная терминология:
- В метрической геометрии автоморфизм — это самоизометрия . Группу автоморфизмов также называют группой изометрий .
- В категории римановых поверхностей автоморфизм — это биголоморфное отображение (также называемое конформным отображением ) поверхности в себя. Например, автоморфизмы сферы Римана являются преобразованиями Мёбиуса .
- Автоморфизм дифференцируемого многообразия M это диффеоморфизм M — в себя. Группу автоморфизмов иногда обозначают Diff( M ).
- В топологии морфизмы между топологическими пространствами называются непрерывными отображениями , а автоморфизм топологического пространства — это гомеоморфизм пространства самому себе, или самогомеоморфизм (см. группу гомеоморфизмов ). В этом примере недостаточно, чтобы морфизм был биективным, чтобы быть изоморфизмом.

История [ править ]

Один из самых ранних групповых автоморфизмов (автоморфизм группы, а не просто группы автоморфизмов точек) был дан ирландским математиком Уильямом Роуэном Гамильтоном в 1856 году в его икосианском исчислении , где он открыл автоморфизм второго порядка: ^[5] письмо:

так что $\mu$ — новый пятый корень единства, связанный с прежним пятым корнем $\lambda$ отношениями совершенной взаимности.

Внутренние и внешние автоморфизмы [ править ]

В некоторых категориях, особенно в группах , кольцах и алгебрах Ли , автоморфизмы можно разделить на два типа, называемые «внутренними» и «внешними» автоморфизмами.

В случае групп внутренние автоморфизмы — это сопряжения элементами самой группы. Для каждого элемента a группы G сопряжение с помощью a - это операция φ _a : G → G , заданная формулой φ _a ( g ) = aga ⁻¹ ( или ⁻¹га ; использование варьируется). Легко проверить, что сопряжение с помощью a является групповым автоморфизмом. Внутренние автоморфизмы образуют нормальную подгруппу группы Aut( G ), обозначаемую Inn( G ); это называется леммой Гурса .

Остальные автоморфизмы называются внешними автоморфизмами . Факторгруппа Aut ( G )/Inn( G ) обычно обозначается Out( G ); нетривиальные элементы — это смежные классы , содержащие внешние автоморфизмы.

То же определение справедливо в любом с единицей кольце или алгебре , где a — любой обратимый элемент . Для алгебр Ли определение немного другое.

См. также [ править ]

Ссылки [ править ]

^ П. Дж. Пал, Р. Дамрат (2001). «§7.5.5 Автоморфизмы» . Математические основы вычислительной техники (перевод Феликса Паля). Спрингер. п. 376. ИСБН 3-540-67995-2 .
^ Йель, Пол Б. (май 1966 г.). «Автоморфизмы комплексных чисел» (PDF) . Журнал «Математика» . 39 (3): 135–141. дои : 10.2307/2689301 . JSTOR 2689301 .
^ Лунесто, Пертти (2001), Клиффордские алгебры и спиноры (2-е изд.), Cambridge University Press, стр. 22–23, ISBN 0-521-00551-5
^ Справочник по алгебре , вып. 3, Эльзевир , 2003, с. 453
^ Сэр Уильям Роуэн Гамильтон (1856 г.). «Меморандум о новой системе корней единства» (PDF) . Философский журнал . 12 : 446. Архивировано (PDF) из оригинала 9 октября 2022 г.

Внешние ссылки [ править ]

[Pahl-1] П. Дж. Пал, Р. Дамрат (2001). «§7.5.5 Автоморфизмы» . Математические основы вычислительной техники (перевод Феликса Паля). Спрингер. п. 376. ИСБН 3-540-67995-2 .

[2] Йель, Пол Б. (май 1966 г.). «Автоморфизмы комплексных чисел» (PDF) . Журнал «Математика» . 39 (3): 135–141. дои : 10.2307/2689301 . JSTOR 2689301 .

[3] Лунесто, Пертти (2001), Клиффордские алгебры и спиноры (2-е изд.), Cambridge University Press, стр. 22–23, ISBN 0-521-00551-5

[4] Справочник по алгебре , вып. 3, Эльзевир , 2003, с. 453

[5] Сэр Уильям Роуэн Гамильтон (1856 г.). «Меморандум о новой системе корней единства» (PDF) . Философский журнал . 12 : 446. Архивировано (PDF) из оригинала 9 октября 2022 г.

[1]

[2]

[3]

[4]

[5]