Векторное пространство

Не путать с векторным полем .

«Линейное пространство» перенаправляется сюда. Чтобы узнать о структуре в геометрии падения, см. Линейное пространство (геометрия) .

Сложение векторов и скалярное умножение: вектор v (синий) добавляется к другому вектору w (красный, верхний рисунок). Ниже w растянуто в 2 раза, что дает сумму v + 2 w .

В математике и физике векторное пространство (также называемое линейным пространством ) — это набор , элементы которого, часто называемые векторами , могут складываться вместе и умножаться («масштабироваться») на числа, называемые скалярами . Скаляры часто являются действительными числами , но могут быть и комплексными числами или, в более общем плане, элементами любого поля . Операции сложения векторов и скалярного умножения должны удовлетворять определенным требованиям, называемым векторными аксиомами . Реальное векторное пространство и комплексное векторное пространство — это виды векторных пространств, основанные на различных видах скаляров: действительное координатное пространство или комплексное координатное пространство .

Векторные пространства обобщают евклидовы векторы , которые позволяют моделировать физические величины , такие как силы и скорость , которые имеют не только величину , но и направление . Концепция векторных пространств является фундаментальной для линейной алгебры вместе с концепцией матриц , которая позволяет выполнять вычисления в векторных пространствах. Это обеспечивает краткий и синтетический способ манипулирования и изучения систем линейных уравнений .

Векторные пространства характеризуются своей размерностью , которая, грубо говоря, задает количество независимых направлений в пространстве. Это означает, что для двух векторных пространств над данным полем и одинаковой размерности свойства, которые зависят только от структуры векторного пространства, совершенно одинаковы (технически векторные пространства изоморфны ) . Векторное пространство является конечномерным, если его размерность является натуральным числом . В противном случае оно бесконечномерно , а его размерность — бесконечный кардинал . Конечномерные векторные пространства естественным образом встречаются в геометрии и смежных областях. Бесконечномерные векторные пространства встречаются во многих областях математики. Например, кольца многочленов представляют собой счетно -бесконечномерные векторные пространства, а многие функциональные пространства имеют мощность континуума в качестве размерности.

Многие векторные пространства, рассматриваемые в математике, наделены и другими структурами . Это случай алгебр , которые включают расширения полей , кольца многочленов, ассоциативные алгебры и алгебры Ли . Это также относится к топологическим векторным пространствам , которые включают функциональные пространства, пространства внутреннего произведения , нормированные пространства , гильбертовы пространства и банаховые пространства .

Определение и основные свойства

В этой статье векторы выделены жирным шрифтом, чтобы отличить их от скаляров.

Векторное пространство над полем F — это непустое множество   V вместе с бинарной операцией и бинарной функцией , которые удовлетворяют восьми аксиомам, перечисленным ниже. В этом контексте элементы V обычно называются векторами , а элементы F называются скалярами .

• Бинарная операция, называемая сложением векторов или просто сложением , присваивает любым двум векторам v и w в V третий вектор из V , который обычно записывается как v + w и называется суммой этих двух векторов.

• Бинарная функция, называемая скалярным умножением , присваивает любому скаляру a из F и любому вектору v из V другой вектор из V , который обозначается как v .

Чтобы иметь векторное пространство, восемь следующих аксиом должны выполняться для всех u , v и w в V , а a и b в F. также

Аксиома	Заявление
Ассоциативность векторного сложения	ты + ( v + ш ) знак равно ( ты + v ) + ш
Коммутативность векторного сложения	u + v = v + u
Идентификатор векторного сложения	Существует элемент 0 € V , называемый нулевым вектором , такой, что + 0 = v для всех v € V. v
Обратные элементы векторного сложения	Для каждого v ∈ V существует элемент − v ∈ V , называемый аддитивным обратным элементу v , такой, что v + (− v ) = 0 .
Совместимость скалярного умножения с умножением полей	a ( b v ) = ( ab ) v
Идентификатор скалярного умножения	1 v = v где 1 обозначает мультипликативное тождество в F. ,
Распределение скалярного умножения относительно сложения векторов	а ( ты + v ) знак равно а ты + а v
Распределение скалярного умножения по сложению полей	( а + б ) v знак равно а v + б v

Когда скалярное поле представляет собой действительные числа , векторное пространство называется действительным векторным пространством , а когда скалярное поле представляет собой комплексные числа , векторное пространство называется комплексным векторным пространством . Эти два случая являются наиболее распространенными, но векторные пространства со скалярами в произвольном поле F. также часто рассматриваются Такое векторное пространство называется F - векторным пространством или над F. векторным пространством

Можно дать эквивалентное определение векторного пространства, которое гораздо более краткое, но менее элементарное: первые четыре аксиомы (относящиеся к сложению векторов) говорят, что векторное пространство представляет собой абелеву группу при сложении, а четыре оставшиеся аксиомы (относящиеся к сложению векторов ) скалярное умножение) говорят, что эта операция определяет гомоморфизм колец из поля F в кольцо эндоморфизмов этой группы.

Вычитание двух векторов можно определить как

$$\mathbf {v} -\mathbf {w} =\mathbf {v} +(-\mathbf {w} ).$$

Прямые следствия аксиом заключаются в том, что для каждого $s\in F$ и $\mathbf {v} \in V,$ надо

• $0\mathbf {v} =\mathbf {0} ,$
• $s\mathbf {0} =\mathbf {0} ,$
• $(-1)\mathbf {v} =-\mathbf {v} ,$
• $s\mathbf {v} =\mathbf {0}$ подразумевает $s=0$ или $\mathbf {v} =\mathbf {0} .$

Если говорить еще более кратко, векторное пространство — это модуль над полем .

Базисы, векторные координаты и подпространства

Вектор v в R ² синий) выраженный через различные основы: с использованием стандартной основы R ( ² : v = x e ₁ + y e ₂ (черный) и с использованием другого, неортогонального базиса : v = f ₁ + f ₂ (красный).

Линейная комбинация

Учитывая набор G элементов F -векторного пространства V , линейная комбинация элементов G является элементом V вида

$$a_{1}\mathbf {g} _{1}+a_{2}\mathbf {g} _{2}+\cdots +a_{k}\mathbf {g} _{k},$$

где $a_{1},\ldots ,a_{k}\in F$ и $\mathbf {g} _{1},\ldots ,\mathbf {g} _{k}\in G.$ Скаляры $a_{1},\ldots ,a_{k}$ называются коэффициентами линейной комбинации.

Линейная независимость

Элементы подмножества G - векторного F пространства V называются линейно независимыми , если ни один элемент G не может быть записан как линейная комбинация других элементов G . Эквивалентно, они линейно независимы, если две линейные комбинации элементов G определяют один и тот же элемент V тогда и только тогда, когда они имеют одинаковые коэффициенты. Аналогичным образом, они линейно независимы, если линейная комбинация приводит к нулевому вектору тогда и только тогда, когда все его коэффициенты равны нулю.

Линейное подпространство

Линейное подпространство или векторное подпространство W векторного пространства V — это непустое подмножество V , замкнутое относительно векторного сложения и скалярного умножения; то есть сумма двух элементов W и произведение элемента W на скаляр принадлежат W . Это означает, что каждая линейная комбинация элементов W принадлежит W . Линейное подпространство — это векторное пространство для индуцированного сложения и скалярного умножения; это означает, что свойство замыкания подразумевает, что аксиомы векторного пространства выполняются.
Свойство замыкания также подразумевает, что каждое пересечение линейных подпространств является линейным подпространством.

Линейный пролет

Учитывая подмножество G векторного пространства V , линейная оболочка или просто оболочка G , является наименьшим линейным подпространством V которое содержит G что это пересечение всех линейных подпространств, содержащих G. , в том смысле , Пространство G также является множеством всех линейных комбинаций элементов G .
Если W является промежутком G , говорят, что охватывает или порождает W и что G является охватывающим множеством или порождающим набором W. G

Основа и размерность

Подмножество векторного пространства является базисом , если его элементы линейно независимы и охватывают векторное пространство. Каждое векторное пространство имеет хотя бы один базис или вообще много (см. Базис (линейная алгебра) § Доказательство того, что каждое векторное пространство имеет базис ). При этом все базы векторного пространства имеют одинаковую мощность , которая называется размерностью векторного пространства (см. Теорему о размерности для векторных пространств ). Это фундаментальное свойство векторных пространств, которое подробно описано в оставшейся части раздела.

Базисы — фундаментальный инструмент для изучения векторных пространств, особенно когда размерность конечна. В бесконечномерном случае существование бесконечных базисов, часто называемых базисами Гамеля , зависит от выбранной аксиомы . Отсюда следует, что, вообще говоря, ни одна база не может быть описана явно. Например, действительные числа образуют бесконечномерное векторное пространство над рациональными числами , для которого неизвестен конкретный базис.

Рассмотрим основу $(\mathbf {b} _{1},\mathbf {b} _{2},\ldots ,\mathbf {b} _{n})$векторного пространства V размерности n над полем F . Определение базиса подразумевает, что каждое $\mathbf {v} \in V$ может быть написано

$$\mathbf {v} =a_{1}\mathbf {b} _{1}+\cdots +a_{n}\mathbf {b} _{n},$$

с $a_{1},\dots ,a_{n}$в F и что это разложение единственно. Скаляры $a_{1},\ldots ,a_{n}$называются координатами v . на базисе Их также называют коэффициентами разложения v по базису. Говорят также, что - набор координат является координатным вектором v n на базисе, поскольку набор $F^{n}$ F n -кортежей элементов является векторным пространством для покомпонентного сложения и скалярного умножения, размерность которого равна n .

Соответствие «один к одному» между векторами и их координатными векторами отображает сложение векторов в сложение векторов, а скалярное умножение — в скалярное умножение. Таким образом, это изоморфизм векторного пространства , который позволяет переводить рассуждения и вычисления над векторами в рассуждения и вычисления над их координатами.

Линейное подпространство или векторное подпространство W векторного пространства V — это непустое подмножество V , замкнутое относительно векторного сложения и скалярного умножения; то есть сумма двух элементов W и произведение элемента W на скаляр принадлежат W . Это означает, что каждая линейная комбинация элементов W принадлежит W . Линейное подпространство — это векторное пространство для индуцированного сложения и скалярного умножения; это означает, что свойство замыкания подразумевает, что аксиомы векторного пространства выполняются. Свойство замыкания также подразумевает, что каждое пересечение линейных подпространств является линейным подпространством.

История

Векторные пространства происходят из аффинной геометрии путем введения координат в плоском или трехмерном пространстве. Около 1636 года французские математики Рене Декарт и Пьер де Ферма основали аналитическую геометрию , находя решения уравнения двух переменных с точками на плоской кривой . Для достижения геометрических решений без использования координат Больцано в 1804 году ввёл некоторые операции над точками, прямыми и плоскостями, которые являются предшественниками векторов. Мёбиус (1827) ввёл понятие барицентрических координат . Беллавитис (1833) ввел отношение эквивалентности для направленных отрезков прямой, имеющих одинаковую длину и направление, которое он назвал равновесием . Тогда евклидов вектор является классом эквивалентности этого отношения.

Векторы были пересмотрены с представлением комплексных чисел Арганом и и Гамильтоном появлением кватернионов . последним Это элементы в R ² и Р ⁴ ; обработка их с помощью линейных комбинаций восходит к Лагерру в 1867 году, который также определил системы линейных уравнений .

В 1857 году Кэли ввёл матричную запись , позволяющую унифицировать и упростить линейные карты . Примерно в то же время Грассман изучал барицентрическое исчисление, начатое Мёбиусом. Он представлял себе наборы абстрактных объектов, наделенных операциями. понятия линейной независимости и размерности , а также скалярных произведений В его работах присутствуют . Работа Грассмана 1844 года также выходит за рамки векторных пространств, поскольку его рассмотрение умножения привело его к тому, что сегодня называется алгебрами . Итальянский математик Пеано был первым, кто дал современное определение векторных пространств и линейных карт в 1888 году. хотя он называл их «линейными системами». Аксиоматизация Пеано допускала векторные пространства с бесконечной размерностью, но Пеано не развивал эту теорию дальше. В 1897 году Сальваторе Пинчерле принял аксиомы Пеано и сделал первые шаги в теории бесконечномерных векторных пространств.

Важным развитием векторных пространств стало создание функциональных пространств Анри Лебегом . Позже это было формализовано Банахом и Гильбертом примерно в 1920 году. В то время алгебра и новая область функционального анализа начали взаимодействовать, особенно с такими ключевыми понятиями, как пространства p -интегрируемых функций и гильбертовы пространства .

Примеры

Основная статья: Примеры векторных пространств

Стрелки в плоскости

сумма v + w (черный) векторов v (синий) и w (красный). Сложение векторов: показана

кратные − v и 2 w . Скалярное умножение: показаны

Первый пример векторного пространства состоит из стрелок в фиксированной плоскости , начинающихся в одной фиксированной точке. Это используется в физике для описания сил или скоростей . Учитывая любые две такие стрелки, v и w , параллелограмм , охватываемый этими двумя стрелками, содержит одну диагональную стрелку, которая также начинается в начале координат. Эта новая стрелка называется суммой двух стрелок и обозначается v + w . В частном случае двух стрелок на одной линии их суммой является стрелка на этой линии, длина которой равна сумме или разности длин в зависимости от того, имеют ли стрелки одинаковое направление. Другая операция, которую можно выполнить со стрелками, — это масштабирование: для любого положительного числа a стрелка, имеющая то же направление, что и v , но расширяющаяся или сжимающаяся в результате умножения ее длины на a , называется умножением на v a действительного . обозначается v . Он Когда a отрицательно, v . определяется как стрелка, указывающая в противоположном направлении

Ниже показано несколько примеров: если a = 2 , результирующий вектор a w имеет то же направление, что и w , но растягивается до двойной длины w (второе изображение). Эквивалентно, 2 w — это сумма w + w . Более того, (−1) v = − v имеет противоположное направление и ту же длину, что и v (синий вектор, направленный вниз на втором изображении).

Упорядоченные пары чисел

Второй ключевой пример векторного пространства — пары действительных чисел x и y . Порядок компонентов x и y имеет значение, поэтому такую ​​пару еще называют упорядоченной парой . Такая пара записывается как ( x , y ) . Сумма двух таких пар и умножение пары на число определяется следующим образом:

$${\begin{aligned}(x_{1},y_{1})+(x_{2},y_{2})&=(x_{1}+x_{2},y_{1}+y_{2}),\\a(x,y)&=(ax,ay).\end{aligned}}$$

Первый пример выше сводится к этому примеру, если стрелка представлена ​​парой декартовых координат ее конечной точки.

Координатное пространство

Простейшим примером векторного пространства над полем F является само поле F , сложение которого рассматривается как сложение векторов, а умножение — как скалярное умножение. В более общем смысле, все n -кортежи (последовательности длины n )

$$(a_{1},a_{2},\dots ,a_{n})$$

элементов a _i из F образуют векторное пространство, которое обычно обозначается F ^н и называется координатным пространством . Случай n = 1 представляет собой упомянутый выше простейший пример, в котором поле F также рассматривается как векторное пространство над собой. Случай F = R и n = 2 (поэтому R ² ) сводится к предыдущему примеру.

Комплексные числа и другие расширения полей

Набор комплексных чисел C , чисел, которые можно записать в виде x + iy для действительных чисел x и y , где i — мнимая единица , образуют векторное пространство над действительными числами с обычным сложением и умножением: ( x + iy ) + ( a + ib ) знак равно ( x + a ) + я ( y + b ) и c ⋅ ( x + iy ) знак равно ( c ⋅ x ) + я ( c ⋅ y ) для действительных чисел x , y , a , b и с . Различные аксиомы векторного пространства следуют из того факта, что одни и те же правила справедливы для арифметики комплексных чисел. Пример комплексных чисел по существу такой же, как (то есть, он изоморфен ) векторному пространству упорядоченных пар действительных чисел, упомянутому выше: если мы думаем о комплексном числе x + i y как о представлении упорядоченной пары ( x , y ) в комплексной плоскости , то мы видим, что правила сложения и скалярного умножения точно соответствуют правилам в предыдущем примере.

В более общем смысле, расширения полей предоставляют другой класс примеров векторных пространств, особенно в алгебре и теории алгебраических чисел : поле F , содержащее меньшее поле E , является E -векторным пространством в соответствии с заданными операциями умножения и сложения F . Например, комплексные числа представляют собой векторное пространство над R , а расширение поля $\mathbf {Q} (i{\sqrt {5}})$ является векторным пространством над Q .

Функциональные пространства

Основная статья: Функциональное пространство

Сложение функций: сумма синуса и показательной функции равна $\sin +\exp :\mathbb {R} \to \mathbb {R}$ с $(\sin +\exp )(x)=\sin(x)+\exp(x)$.

Функции из любого фиксированного множества Ω в поле F также образуют векторные пространства, выполняя поточечное сложение и скалярное умножение. То есть сумма двух функций f и g есть функция $(f+g)$ данный

$$(f+g)(w)=f(w)+g(w),$$

и аналогично для умножения. Такие функциональные пространства встречаются во многих геометрических ситуациях, когда — действительная прямая , интервал или подмножества R. другие Ω Многие понятия в топологии и анализе, такие как непрерывность , интегрируемость или дифференцируемость, хорошо относятся к линейности: суммы и скалярные кратные функции, обладающие таким свойством, по-прежнему обладают этим свойством. Поэтому множеством таких функций являются векторные пространства, изучение которых относится к функциональному анализу .

Линейные уравнения

Основные статьи: Линейное уравнение , Линейное дифференциальное уравнение и Системы линейных уравнений.

Системы однородных линейных уравнений тесно связаны с векторными пространствами. Например, решения

$${\begin{alignedat}{9}&&a\,&&+\,3b\,&\,+&\,&c&\,=0\\4&&a\,&&+\,2b\,&\,+&\,2&c&\,=0\\\end{alignedat}}$$

задаются тройками с произвольными $a,$ $b=a/2,$ и $c=-5a/2.$Они образуют векторное пространство: суммы и скалярные кратные таких троек по-прежнему удовлетворяют тем же отношениям трех переменных; таким образом, они тоже являются решениями. Матрицы можно использовать для объединения нескольких линейных уравнений, как указано выше, в одно векторное уравнение, а именно

$$A\mathbf {x} =\mathbf {0} ,$$

где $A={\begin{bmatrix}1&3&1\\4&2&2\end{bmatrix}}$ – матрица, содержащая коэффициенты данных уравнений, $\mathbf {x}$ вектор $(a,b,c),$ $A\mathbf {x}$ обозначает матричное произведение и $\mathbf {0} =(0,0)$– нулевой вектор. Аналогичным образом решения однородных линейных дифференциальных уравнений образуют векторные пространства. Например,

$$f^{\prime \prime }(x)+2f^{\prime }(x)+f(x)=0$$

урожайность $f(x)=ae^{-x}+bxe^{-x},$ где $a$ и $b$ являются произвольными константами, а $e^{x}$ – естественная показательная функция .

Линейные карты и матрицы

Основная статья: Линейная карта

Отношения двух векторных пространств могут быть выражены линейным отображением или линейным преобразованием . Это функции , отражающие структуру векторного пространства, то есть сохраняющие суммы и скалярное умножение:

$${\begin{aligned}f(\mathbf {v} +\mathbf {w} )&=f(\mathbf {v} )+f(\mathbf {w} ),\\f(a\cdot \mathbf {v} )&=a\cdot f(\mathbf {v} )\end{aligned}}$$

для всех $\mathbf {v}$ и $\mathbf {w}$ в $V,$ все $a$ в $F.$

Изоморфизм обратное — это линейное отображение f : V → W такое, что существует отображение g : W → V , которое является отображением таким, что две возможные композиции f ∘ g : W → W и g ∘ f : V → V равны карты личности . Эквивалентно, f является одновременно взаимно однозначным ( инъективным ) и на ( сюръективным ). Если существует изоморфизм между V и W , эти два пространства называются изоморфными ; тогда они по существу идентичны как векторные пространства, поскольку все тождества, содержащиеся в V , через f переносятся в аналогичные в W и наоборот через g .

Описание вектора стрелки v его координатами x и y дает изоморфизм векторных пространств.

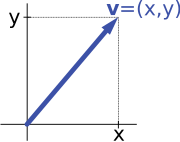
Например, стрелки на плоскости и упорядоченные пары векторных пространств чисел во введении выше (см. § Примеры ) изоморфны: плоская стрелка v, выходящая из начала некоторой (фиксированной) системы координат, может быть выражена как упорядоченная пара рассматривая компоненты x и y стрелки, как показано на изображении справа. И наоборот, для пары ( x , y ) стрелка, идущая вдоль x вправо (или влево, если x отрицательный) и y вверх (вниз, если y отрицательный), поворачивает стрелку v назад .

Линейные отображения V → W между двумя векторными пространствами образуют векторное пространство Hom _F ( V , W ) , также обозначаемое L( V , W ) или 𝓛( V , W ) . Пространство линейных отображений из V в F называется двойственным векторным пространством , обозначается V ^∗ . Через инъективное естественное отображение V → V ^∗∗ любое векторное пространство можно вложить в свое бидуальное пространство ; отображение является изоморфизмом тогда и только тогда, когда пространство конечномерно.

базиса V После выбора линейные отображения f : V → W полностью определяются путем указания образов базисных векторов, поскольку любой элемент V однозначно выражается как их линейная комбинация. Если dim V = dim W , соответствие 1 к 1 между фиксированными базисами V и W приводит к линейному отображению, которое отображает любой базисный элемент V в соответствующий базисный элемент W . Это изоморфизм по самому своему определению. Следовательно, два векторных пространства над данным полем изоморфны, если их размерности совпадают, и наоборот. Другой способ выразить это состоит в том, что любое векторное пространство над данным полем полностью классифицируется ( с точностью до изоморфизма) по своей размерности, одному числу. В частности, любое n -мерное F -векторное пространство V изоморфно F ^н . Однако не существует «канонического» или предпочтительного изоморфизма; изоморфизм φ : F ^н → V эквивалентно выбору базиса V путем отображения стандартного базиса F ^н к V через φ .

Матрицы

Основные статьи: Матрица и определитель

Типичная матрица

Матрицы — полезное понятие для кодирования линейных карт. Они записываются в виде прямоугольного массива скаляров, как показано на изображении справа. Любая m - n матрица $A$ порождает линейное отображение из F ^н до F ^м , следующим

$$\mathbf {x} =(x_{1},x_{2},\ldots ,x_{n})\mapsto \left(\sum _{j=1}^{n}a_{1j}x_{j},\sum _{j=1}^{n}a_{2j}x_{j},\ldots ,\sum _{j=1}^{n}a_{mj}x_{j}\right),$$

где ${\textstyle \sum }$ обозначает суммирование или с помощью матричного умножения матрицы $A$ с координатным вектором $\mathbf {x}$:

$$\mathbf {x} \mapsto A\mathbf {x} .$$

после выбора базисов V и W Более того , любое линейное отображение f : V → W однозначно представляется матрицей с помощью этого присваивания.

Объем этого параллелепипеда является абсолютным значением определителя матрицы 3х3, образованной векторами r ₁ , r ₂ и r ₃ .

Определитель det ( A ) квадратной матрицы A является скаляром, который сообщает, является ли связанное отображение изоморфизмом или нет: для этого достаточно и необходимо, чтобы определитель был ненулевым. Линейное преобразование R ^н соответствующая вещественной размера n x n матрице , сохраняет ориентацию тогда и только тогда, когда ее определитель положителен.

Собственные значения и собственные векторы

Основная статья: Собственные значения и собственные векторы

Эндоморфизмы , линейные отображения f : V → V , особенно важны, поскольку в этом случае векторы v можно сравнить с их образом при f , f ( v ) . Любой ненулевой вектор v, удовлетворяющий λ v = f ( v ) , где λ — скаляр, называется вектором собственным f с собственным значением λ . Эквивалентно, v является элементом ядра разности f − λ · Id (где Id — тождественное отображение V → V ) . Если V конечномерно, это можно перефразировать с помощью определителей: f , имеющее собственное значение λ , эквивалентно

$$\det(f-\lambda \cdot \operatorname {Id} )=0.$$

Разъясняя определение определителя, можно увидеть, что выражение в левой части представляет собой полиномиальную функцию от λ , называемую характеристическим полиномом функции f . Если поле F достаточно велико, чтобы содержать нуль этого многочлена (что автоматически происходит для F алгебраически замкнутого , такого как F = C ), любое линейное отображение имеет хотя бы один собственный вектор. Векторное пространство V может иметь или не иметь собственный базис , состоящий из собственных векторов. Это явление регулируется жордановой канонической формой карты. Набор всех собственных векторов, соответствующих определенному собственному значению f, образует векторное пространство, известное как собственное пространство , соответствующее собственному значению (и f рассматриваемому ).

Основные конструкции

Помимо приведенных выше конкретных примеров, существует ряд стандартных линейных алгебраических конструкций, дающих векторные пространства, связанные с заданными.

Подпространства и факторпространства

Основные статьи: Линейное подпространство и факторвекторное пространство

Линия, проходящая через начало координат (синяя, толстая) в R ³ является линейным подпространством. Это пересечение двух плоскостей (зеленой и желтой).

Непустое подмножество $W$ векторного пространства $V$ замкнутый относительно сложения и скалярного умножения (и, следовательно, содержащий $\mathbf {0}$-вектор $V$) называется линейным подпространством $V$или подпространство просто $V$, когда окружающее пространство однозначно является векторным пространством. Подпространства $V$сами по себе являются векторными пространствами (над тем же полем). Пересечение всех подпространств, содержащих данное множество $S$ векторов называется его промежутком и является наименьшим подпространством $V$ содержащий набор $S$. Выражаясь в элементах, пролет — это подпространство, состоящее из всех линейных комбинаций элементов $S$.

Линейное подпространство размерности 1 и 2 называется линией (также векторной линией ) и плоскостью соответственно. Если W — n -мерное векторное пространство, то любое подпространство размерности на 1 меньше, т. е. размерности $n-1$ называется гиперплоскостью .

Аналогом подпространств являются факторвекторные пространства . Учитывая любое подпространство $W\subseteq V$, факторпространство $V/W$ (« $V$ модуль $W$") определяется следующим образом: как множество оно состоит из

$$\mathbf {v} +W=\{\mathbf {v} +\mathbf {w} :\mathbf {w} \in W\},$$

где $\mathbf {v}$ — произвольный вектор в $V$. Сумма двух таких элементов $\mathbf {v} _{1}+W$ и $\mathbf {v} _{2}+W$ является $\left(\mathbf {v} _{1}+\mathbf {v} _{2}\right)+W$, а скалярное умножение определяется выражением $a\cdot (\mathbf {v} +W)=(a\cdot \mathbf {v} )+W$. Ключевым моментом в этом определении является то, что $\mathbf {v} _{1}+W=\mathbf {v} _{2}+W$ тогда и только тогда, когда разница $\mathbf {v} _{1}$ и $\mathbf {v} _{2}$ заключается в $W$. Таким образом, факторпространство «забывает» информацию, содержащуюся в подпространстве. $W$.

Ядро ​ $\ker(f)$ линейной карты $f:V\to W$ состоит из векторов $\mathbf {v}$ которые сопоставлены с $\mathbf {0}$ в $W$. Ядро и образ $\operatorname {im} (f)=\{f(\mathbf {v} ):\mathbf {v} \in V\}$ являются подпространствами $V$ и $W$, соответственно.

Важным примером является ядро ​​линейного отображения. $\mathbf {x} \mapsto A\mathbf {x}$ для некоторой фиксированной матрицы $A$. Ядром этого отображения является подпространство векторов $\mathbf {x}$ такой, что $A\mathbf {x} =\mathbf {0}$, что и есть совокупность решений системы однородных линейных уравнений, принадлежащих $A$. Эта концепция распространяется и на линейные дифференциальные уравнения.

$$a_{0}f+a_{1}{\frac {df}{dx}}+a_{2}{\frac {d^{2}f}{dx^{2}}}+\cdots +a_{n}{\frac {d^{n}f}{dx^{n}}}=0,$$

где коэффициенты $a_{i}$ являются функциями в $x,$слишком. На соответствующей карте

$$f\mapsto D(f)=\sum _{i=0}^{n}a_{i}{\frac {d^{i}f}{dx^{i}}},$$

производные ​ функции $f$ выглядят линейно (в отличие от $f^{\prime \prime }(x)^{2}$, например). Поскольку дифференцирование является линейной процедурой (т. е. $(f+g)^{\prime }=f^{\prime }+g^{\prime }$ и $(c\cdot f)^{\prime }=c\cdot f^{\prime }$ для постоянного $c$) это присвоение является линейным и называется линейным дифференциальным оператором . В частности, решения дифференциального уравнения $D(f)=0$ образуют векторное пространство (над R или C ).

Существование ядер и образов является частью утверждения о том, что категория векторных пространств (над фиксированным полем $F$) — абелева категория , то есть совокупность математических объектов и сохраняющих структуру отображений между ними ( категория ), которая ведет себя во многом аналогично категории абелевых групп . Из-за этого многие утверждения, такие как первая теорема об изоморфизме (также называемая теоремой о ранге-нулевости в терминах, связанных с матрицами),

$$V/\ker(f)\;\equiv \;\operatorname {im} (f)$$

а вторая и третья теоремы об изоморфизме могут быть сформулированы и доказаны способом, очень похожим на соответствующие утверждения для групп .

Прямой продукт

Основные статьи: Прямой продукт и Прямая сумма модулей.

Прямое произведение векторных пространств и прямая сумма векторных пространств — это два способа объединения индексированного семейства векторных пространств в новое векторное пространство.

Прямой продукт $\textstyle {\prod _{i\in I}V_{i}}$ семейства векторных пространств $V_{i}$ состоит из множества всех кортежей $\left(\mathbf {v} _{i}\right)_{i\in I}$, которые указывают для каждого индекса $i$ в некотором наборе индексов $I$ элемент $\mathbf {v} _{i}$ из $V_{i}$. Сложение и скалярное умножение выполняются покомпонентно. Вариантом этой конструкции является прямая сумма ${\textstyle \bigoplus _{i\in I}V_{i}}$ (также называемый копродукцией и обозначаемый ${\textstyle \coprod _{i\in I}V_{i}}$), где разрешены только кортежи с конечным числом ненулевых векторов. Если индекс установлен $I$ конечно, обе конструкции согласуются, но в общем случае они различны.

Тензорное произведение

Основная статья: Тензорное произведение векторных пространств

Тензорное произведение $V\otimes _{F}W,$ или просто $V\otimes W,$ двух векторных пространств $V$ и $W$- одно из центральных понятий полилинейной алгебры , которое касается расширения таких понятий, как линейные отображения, на несколько переменных. Карта $g:V\times W\to X$ из декартова произведения $V\times W$ называется билинейным, если $g$ линейна по обеим переменным $\mathbf {v}$ и $\mathbf {w} .$ То есть для фиксированного $\mathbf {w}$ карта $\mathbf {v} \mapsto g(\mathbf {v} ,\mathbf {w} )$ является линейным в указанном выше смысле, а также при фиксированном $\mathbf {v} .$

Коммутативная диаграмма , изображающая универсальное свойство тензорного произведения

Тензорное произведение — это особое векторное пространство, которое является универсальным получателем билинейных отображений. $g,$следующее. Оно определяется как векторное пространство, состоящее из конечных (формальных) сумм символов, называемых тензорами.

$$\mathbf {v} _{1}\otimes \mathbf {w} _{1}+\mathbf {v} _{2}\otimes \mathbf {w} _{2}+\cdots +\mathbf {v} _{n}\otimes \mathbf {w} _{n},$$

согласно правилам

$${\begin{alignedat}{6}a\cdot (\mathbf {v} \otimes \mathbf {w} )~&=~(a\cdot \mathbf {v} )\otimes \mathbf {w} ~=~\mathbf {v} \otimes (a\cdot \mathbf {w} ),&&~~{\text{ where }}a{\text{ is a scalar}}\\(\mathbf {v} _{1}+\mathbf {v} _{2})\otimes \mathbf {w} ~&=~\mathbf {v} _{1}\otimes \mathbf {w} +\mathbf {v} _{2}\otimes \mathbf {w} &&\\\mathbf {v} \otimes (\mathbf {w} _{1}+\mathbf {w} _{2})~&=~\mathbf {v} \otimes \mathbf {w} _{1}+\mathbf {v} \otimes \mathbf {w} _{2}.&&\\\end{alignedat}}$$

Эти правила гарантируют, что карта $f$ из $V\times W$ к $V\otimes W$ это отображает кортеж $(\mathbf {v} ,\mathbf {w} )$ к $\mathbf {v} \otimes \mathbf {w}$является билинейным. Универсальность утверждает, что для любого векторного пространства $X$ и любое билинейное отображение $g:V\times W\to X,$ существует уникальная карта $u,$ показано на схеме пунктирной стрелкой, состав которой с $f$ равно $g:$ $u(\mathbf {v} \otimes \mathbf {w} )=g(\mathbf {v} ,\mathbf {w} ).$ Это называется универсальным свойством тензорного произведения, экземпляром метода, широко используемого в продвинутой абстрактной алгебре, для косвенного определения объектов путем указания карт от этого объекта или к нему.

Векторные пространства с дополнительной структурой

С точки зрения линейной алгебры векторные пространства понимаются вполне постольку, поскольку любое векторное пространство над данным полем характеризуется с точностью до изоморфизма своей размерностью. Однако векторные пространства сами по себе ли последовательность функций не предлагают основу для решения крайне важного для анализа вопроса: сходится к другой функции. Точно так же линейная алгебра не приспособлена для работы с бесконечными рядами , поскольку операция сложения позволяет добавлять только конечное число членов. Поэтому потребности функционального анализа требуют рассмотрения дополнительных структур.

Векторному пространству можно придать частичный порядок. $\,\leq ,\,$ при котором можно сравнивать некоторые векторы. Например, $n$трехмерное реальное пространство $\mathbf {R} ^{n}$можно упорядочить, сравнивая его векторы покомпонентно. Упорядоченные векторные пространства , например пространства Рисса , имеют фундаментальное значение для интегрирования Лебега , которое основано на способности выражать функцию как разность двух положительных функций.

$$f=f^{+}-f^{-}.$$

где $f^{+}$ обозначает положительную часть $f$ и $f^{-}$ отрицательная часть.

Нормированные векторные пространства и пространства внутренних произведений

Основные статьи: Нормированное векторное пространство и пространство внутреннего произведения

«Измерение» векторов осуществляется путем указания нормы , базы данных, которая измеряет длину векторов, или внутреннего продукта , который измеряет углы между векторами. Нормы и внутренние продукты обозначаются $|\mathbf {v} |$ и $\langle \mathbf {v} ,\mathbf {w} \rangle ,$соответственно. Данные внутреннего продукта подразумевают, что длины векторов также могут быть определены путем определения соответствующей нормы ${\textstyle |\mathbf {v} |:={\sqrt {\langle \mathbf {v} ,\mathbf {v} \rangle }}.}$ Векторные пространства, наделенные такими данными, известны как нормированные векторные пространства и пространства внутреннего продукта соответственно.

Координатное пространство $F^{n}$ может быть оснащен стандартным скалярным произведением :

$$\langle \mathbf {x} ,\mathbf {y} \rangle =\mathbf {x} \cdot \mathbf {y} =x_{1}y_{1}+\cdots +x_{n}y_{n}.$$

В $\mathbf {R} ^{2},$ это отражает общее представление об угле между двумя векторами $\mathbf {x}$ и $\mathbf {y} ,$ по закону косинусов :

$$\mathbf {x} \cdot \mathbf {y} =\cos \left(\angle (\mathbf {x} ,\mathbf {y} )\right)\cdot |\mathbf {x} |\cdot |\mathbf {y} |.$$

Поэтому два вектора, удовлетворяющие $\langle \mathbf {x} ,\mathbf {y} \rangle =0$называются ортогональными . используется важный вариант стандартного скалярного произведения В пространстве Минковского : $\mathbf {R} ^{4}$ наделенный произведением Лоренца

$$\langle \mathbf {x} |\mathbf {y} \rangle =x_{1}y_{1}+x_{2}y_{2}+x_{3}y_{3}-x_{4}y_{4}.$$

В отличие от стандартного скалярного произведения, оно не является положительно определенным : $\langle \mathbf {x} |\mathbf {x} \rangle$ также принимает отрицательные значения, например, для $\mathbf {x} =(0,0,0,1).$ Выделение четвертой координаты, соответствующей времени , а не трем пространственным измерениям, делает ее полезной для математической обработки специальной теории относительности .

Топологические векторные пространства

Основная статья: Топологическое векторное пространство

Вопросы сходимости решаются путем рассмотрения векторных пространств. $V$ несущая совместимую топологию , структуру, позволяющую говорить об элементах, находящихся близко друг к другу . Совместимость здесь означает, что сложение и скалярное умножение должны быть непрерывными отображениями . Примерно, если $\mathbf {x}$ и $\mathbf {y}$ в $V$, и $a$ в $F$ изменяются на ограниченную величину, то также $\mathbf {x} +\mathbf {y}$ и $a\mathbf {x} .$ Чтобы иметь смысл указывать величину изменения скаляра, поле $F$также должен иметь топологию в этом контексте; общий выбор — действительные или комплексные числа.

В таких топологических векторных пространствах можно рассматривать серии векторов. Бесконечная сумма

$$\sum _{i=1}^{\infty }f_{i}~=~\lim _{n\to \infty }f_{1}+\cdots +f_{n}$$

обозначает предел соответствующих конечных частичных сумм последовательности $f_{1},f_{2},\ldots$ элементов $V.$ Например, $f_{i}$ могут быть (действительные или комплексные) функции, принадлежащие некоторому функциональному пространству $V,$в этом случае ряд является функциональным рядом . Способ сходимости ряда зависит от топологии, наложенной на функциональное пространство. В таких случаях поточечная и равномерная сходимость . двумя яркими примерами являются

Единица «сферы» в $\mathbf {R} ^{2}$ состоят из плоских векторов нормы 1. Изображены единичные сферы в разных $p$-нормы , для $p=1,2,$ и $\infty .$ На большем ромбе изображены точки 1-нормы, равные 2.

Способ гарантировать существование пределов некоторых бесконечных серий — это ограничить внимание пространствами, где любая последовательность Коши имеет предел; такое векторное пространство называется полным . Грубо говоря, векторное пространство является полным, если оно содержит все необходимые пределы. Например, векторное пространство полиномов на единичном интервале $[0,1],$ снабженная топологией равномерной сходимости, не является полной, поскольку любая непрерывная функция на $[0,1]$ может быть равномерно аппроксимирован последовательностью полиномов по аппроксимационной теореме Вейерштрасса . Напротив, пространство всех непрерывных функций на $[0,1]$ с той же топологией является полным. Норма порождает топологию, определяя, что последовательность векторов $\mathbf {v} _{n}$ сходится к $\mathbf {v}$ если и только если

$$\lim _{n\to \infty }|\mathbf {v} _{n}-\mathbf {v} |=0.$$

Банахово и гильбертово пространства — это полные топологические векторные пространства, топологии которых задаются соответственно нормой и скалярным произведением. Их исследование — ключевая часть функционального анализа — сосредоточено на бесконечномерных векторных пространствах, поскольку все нормы в конечномерных топологических векторных пространствах порождают одно и то же понятие сходимости. Изображение справа показывает эквивалентность $1$-норма и $\infty$-норма на $\mathbf {R} ^{2}:$поскольку единичные «шарики» заключают друг в друга, последовательность сходится к нулю в одной норме тогда и только тогда, когда это происходит в другой норме. Однако в бесконечномерном случае, как правило, будут неэквивалентные топологии, что делает изучение топологических векторных пространств более богатым, чем исследование векторных пространств без дополнительных данных.

С концептуальной точки зрения все понятия, связанные с топологическими векторными пространствами, должны соответствовать топологии. Например, вместо рассмотрения всех линейных отображений (также называемых функционалами ) $V\to W,$ карты между топологическими векторными пространствами должны быть непрерывными. В частности, (топологическое) дуальное пространство $V^{*}$ состоит из непрерывных функционалов $V\to \mathbf {R}$ (или чтобы $\mathbf {C}$). Фундаментальная теорема Хана – Банаха касается разделения подпространств соответствующих топологических векторных пространств непрерывными функционалами.

Банаховы пространства

Основная статья: Банахово пространство

Банаховы пространства , введенные Стефаном Банахом , являются полными нормированными векторными пространствами.

Первый пример — векторное пространство $\ell ^{p}$ состоящий из бесконечных векторов с реальными элементами $\mathbf {x} =\left(x_{1},x_{2},\ldots ,x_{n},\ldots \right)$ чей $p$-норма $(1\leq p\leq \infty )$ данный

$$\|\mathbf {x} \|_{\infty }:=\sup _{i}|x_{i}|\qquad {\text{ for }}p=\infty ,{\text{ and }}$$

$$\|\mathbf {x} \|_{p}:=\left(\sum _{i}|x_{i}|^{p}\right)^{\frac {1}{p}}\qquad {\text{ for }}p<\infty .$$

Топологии в бесконечномерном пространстве $\ell ^{p}$ неэквивалентны для разных $p.$ Например, последовательность векторов $\mathbf {x} _{n}=\left(2^{-n},2^{-n},\ldots ,2^{-n},0,0,\ldots \right),$ в котором первый $2^{n}$ компоненты $2^{-n}$ и следующие $0,$ сходится к нулевому вектору для $p=\infty ,$ но не для $p=1:$

$$\|\mathbf {x} _{n}\|_{\infty }=\sup(2^{-n},0)=2^{-n}\to 0,$$

но

$$\|\mathbf {x} _{n}\|_{1}=\sum _{i=1}^{2^{n}}2^{-n}=2^{n}\cdot 2^{-n}=1.$$

В более общем смысле, чем последовательности действительных чисел, функции $f:\Omega \to \mathbb {R}$ наделены нормой, заменяющей указанную сумму на интеграл Лебега

$$\|f\|_{p}:=\left(\int _{\Omega }|f(x)|^{p}\,{d\mu (x)}\right)^{\frac {1}{p}}.$$

Пространство интегрируемых функций в заданной области $\Omega$ (например, интервал), удовлетворяющий $\|f\|_{p}<\infty ,$ и снабженные этой нормой, называются пространствами Лебега и обозначаются $L^{\;\!p}(\Omega ).$

Эти пространства полны. (Если вместо этого использовать интеграл Римана , пространство не будет полным, что можно рассматривать как оправдание теории интеграции Лебега. ) Конкретно это означает, что для любой последовательности интегрируемых по Лебегу функций $f_{1},f_{2},\ldots ,f_{n},\ldots$ с $\|f_{n}\|_{p}<\infty ,$ удовлетворяющее условию

$$\lim _{k,\ n\to \infty }\int _{\Omega }\left|f_{k}(x)-f_{n}(x)\right|^{p}\,{d\mu (x)}=0$$

существует функция $f(x)$ принадлежащий векторному пространству $L^{\;\!p}(\Omega )$ такой, что

$$\lim _{k\to \infty }\int _{\Omega }\left|f(x)-f_{k}(x)\right|^{p}\,{d\mu (x)}=0.$$

Наложение условий ограниченности не только на функцию, но и на ее производные приводит к пространствам Соболева .

Гильбертовы пространства

Основная статья: Гильбертово пространство

На следующих снимках показано суммирование от 1 до 5 членов при аппроксимации периодической функции (синий) конечной суммой синусоидальных функций (красный).

Полные пространства внутреннего произведения известны как гильбертовы пространства , в честь Дэвида Гильберта . Гильбертово пространство $L^{2}(\Omega ),$ с внутренним продуктом, заданным выражением

$$\langle f\ ,\ g\rangle =\int _{\Omega }f(x){\overline {g(x)}}\,dx,$$

где ${\overline {g(x)}}$ обозначает комплексно-сопряженное число $g(x),$ это ключевой случай.

По определению, в гильбертовом пространстве любая последовательность Коши сходится к пределу. Обратно, найдя последовательность функций $f_{n}$с желаемыми свойствами, которые аппроксимируют заданную предельную функцию, не менее важно. Ранний анализ под видом аппроксимации Тейлора установил приближение дифференцируемых функций. $f$ полиномами. По теореме Стоуна–Вейерштрасса каждая непрерывная функция на $[a,b]$ может быть сколь угодно близко аппроксимирован полиномом. Подобный метод аппроксимации тригонометрическими функциями обычно называется расширением Фурье и широко применяется в технике. В более общем и концептуальном плане теорема дает простое описание того, какие «базовые функции» или, в абстрактных гильбертовых пространствах, какие базовые векторы достаточны для создания гильбертова пространства. $H,$в том смысле, что замыканием их промежутка (т. е. конечных линейных комбинаций и их пределов) является все пространство. Такой набор функций базисом называется $H,$ его мощность известна как размерность гильбертова пространства . Теорема не только показывает подходящие базисные функции, достаточные для целей аппроксимации, но также вместе с процессом Грама – Шмидта позволяет построить базис ортогональных векторов . Такие ортогональные базисы являются обобщением координатных осей гильбертова пространства в конечномерном евклидовом пространстве .

Решения различных дифференциальных уравнений можно интерпретировать в терминах гильбертовых пространств. Например, очень многие области физики и техники приводят к таким уравнениям, и часто решения с определенными физическими свойствами используются в качестве базисных функций, часто ортогональных. В качестве примера из физики, зависящее от времени уравнение Шредингера в квантовой механике описывает изменение физических свойств во времени с помощью уравнения в частных производных , решения которого называются волновыми функциями . Определенные значения физических свойств, таких как энергия или импульс, соответствуют собственным значениям определенного (линейного) дифференциального оператора , а соответствующие волновые функции называются собственными состояниями . Спектральная теорема разлагает линейный компактный оператор, действующий на функции, через эти собственные функции и их собственные значения.

Алгебры над полями

Основные статьи: Алгебра над полем и алгебра Ли

Гипербола , заданная уравнением $x\cdot y=1.$ Координатное кольцо функций на этой гиперболе имеет вид $\mathbf {R} [x,y]/(x\cdot y-1),$ бесконечномерное векторное пространство над $\mathbf {R} .$

Общие векторные пространства не обладают умножением между векторами. Векторное пространство, снабженное дополнительным билинейным оператором , определяющим умножение двух векторов, является алгеброй над полем (или F -алгеброй, если поле F задано).

Например, множество всех полиномов $p(t)$образует алгебру, известную как кольцо многочленов : используя то, что сумма двух многочленов является многочленом, они образуют векторное пространство; они образуют алгебру, поскольку произведение двух многочленов снова является многочленом. Кольца многочленов (от нескольких переменных) и их частных составляют основу алгебраической геометрии , поскольку они являются кольцами функций алгебро-геометрических объектов .

Другим важным примером являются алгебры Ли , которые не являются ни коммутативными, ни ассоциативными, но неспособность быть таковой ограничена ограничениями ( $[x,y]$ обозначает произведение $x$ и $y$):

• $[x,y]=-[y,x]$ ( антикоммутативность ) и
• $[x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0$ ( тождество Якоби ).

Примеры включают векторное пространство $n$-к- $n$ матрицы, с $[x,y]=xy-yx,$ коммутатор и двух матриц $\mathbf {R} ^{3},$ наделен векторным произведением .

Тензорная алгебра $\operatorname {T} (V)$ это формальный способ добавления продуктов в любое векторное пространство $V$ чтобы получить алгебру. Как векторное пространство, оно состоит из символов, называемых простыми тензорами.

$$\mathbf {v} _{1}\otimes \mathbf {v} _{2}\otimes \cdots \otimes \mathbf {v} _{n},$$

где степень $n$варьируется. Умножение задается путем объединения таких символов, наложения закона распределения при сложении и требования, чтобы скалярное умножение коммутировало с тензорным произведением ⊗, почти так же, как с тензорным произведением двух векторных пространств, введенным в приведенном выше разделе о тензорных произведениях . В общем, никаких отношений между $\mathbf {v} _{1}\otimes \mathbf {v} _{2}$ и $\mathbf {v} _{2}\otimes \mathbf {v} _{1}.$ Принуждение двух таких элементов к равенству приводит к симметричной алгебре , тогда как принуждение к равенству двух таких элементов приводит к симметричной алгебре. $\mathbf {v} _{1}\otimes \mathbf {v} _{2}=-\mathbf {v} _{2}\otimes \mathbf {v} _{1}$ дает внешнюю алгебру .

Связанные структуры

Векторные пучки

Основные статьи: Векторное расслоение и Касательное расслоение

Лента Мёбиуса. Локально это выглядит U × R. как

Векторное расслоение — это семейство векторных пространств, непрерывно параметризованных топологическим пространством X . Точнее, векторное расслоение над X — это топологическое пространство E, снабженное непрерывным отображением

$$\pi :E\to X$$

что для любого x в X слой π такой , ⁻¹ ( x ) — векторное пространство. Случай dim V = 1 называется линейным расслоением . Для любого векторного пространства V проекция X × V → X превращает произведение X × V в «тривиальное» векторное расслоение . Векторные расслоения над X должны быть локально продуктом X и некоторого (фиксированного) векторного пространства V : для каждого x в X существует окрестность U точки x такая, что ограничение π на π ⁻¹ ( U ) изоморфен тривиальному расслоению U × V → U . Несмотря на свой локально тривиальный характер, векторные расслоения могут (в зависимости от формы основного пространства X ) быть «перекручены» в большом (т. е. расслоение не обязательно должно быть (глобально изоморфным) тривиальному расслоению X × V ). Например, ленту Мёбиуса можно рассматривать как расслоение над окружностью S. ¹ (путем отождествления открытых интервалов с реальной линией ). Однако он отличается от цилиндра S. ¹ × R , поскольку последний ориентируем , а первый — нет.

Свойства определенных векторных расслоений предоставляют информацию о базовом топологическом пространстве. Например, касательное расслоение состоит из совокупности касательных пространств , параметризованных точками дифференцируемого многообразия. Касательное расслоение окружности S ¹ глобально изоморфен S ¹ × R существует глобальное ненулевое векторное поле , поскольку на S ¹ . Напротив, по теореме о волосатом шаре не существует (касательного) векторного поля . на 2-сфере S ² которое везде не равно нулю. K-теория изучает классы изоморфизма всех векторных расслоений в некотором топологическом пространстве. он имеет чисто алгебраические последствия, такие как классификация конечномерных вещественных алгебр с делением : R , C , кватернионов H и октонионов O. Помимо углубления топологического и геометрического понимания ,

Кокасательное расслоение дифференцируемого многообразия состоит в каждой точке многообразия из двойственного к касательному пространству — кокасательного пространства . Секции этого расслоения известны как дифференциальные одноформы .

Модули

Основная статья: Модуль

Модули для колец — то же самое, что векторные пространства для полей: те же аксиомы, примененные к кольцу R вместо поля F , дают модули. Теория модулей по сравнению с теорией векторных пространств усложняется наличием кольцевых элементов, не имеющих мультипликативных обратных . Например, модулям не обязательно иметь базы, как показывает Z -модуль (т. е. абелева группа ) Z /2 Z ; те модули, которые это делают (включая все векторные пространства), известны как свободные модули . Тем не менее, векторное пространство можно компактно определить как модуль над кольцом , которое является полем , элементы которого называются векторами. Некоторые авторы используют термин «векторное пространство» для обозначения модулей над телом . Алгебро-геометрическая интерпретация коммутативных колец через их спектр позволяет развивать такие концепции, как локально свободные модули , алгебраический аналог векторных расслоений.

Аффинные и проективные пространства

Основные статьи: Аффинное пространство и Проективное пространство

Аффинная плоскость (голубая) в R ³ . Это двумерное подпространство, сдвинутое на вектор x (красный).

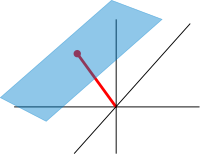
Грубо говоря, аффинные пространства — это векторные пространства, происхождение которых не указано. Точнее, аффинное пространство — это множество со свободным транзитивным векторного пространства действием . В частности, векторное пространство является аффинным пространством над самим собой по отображению

$$V\times V\to W,\;(\mathbf {v} ,\mathbf {a} )\mapsto \mathbf {a} +\mathbf {v} .$$

Если W — векторное пространство, то аффинное подпространство — это подмножество W , полученное переводом линейного подпространства V на фиксированный вектор x ∈ W ; это пространство обозначается x + V (оно является классом смежным V в W ) и состоит из всех векторов вида x + v для v ∈ V . Важным примером является пространство решений системы неоднородных линейных уравнений

$$A\mathbf {v} =\mathbf {b}$$

обобщая однородный случай, обсуждавшийся в предыдущем разделе о линейных уравнениях, который можно найти, положив $\mathbf {b} =\mathbf {0}$ в этом уравнении. Пространство решений — это аффинное подпространство x + V где x — частное решение уравнения, а V — пространство решений однородного уравнения ( нулевое пространство A , ).

Набор одномерных подпространств фиксированного конечномерного векторного пространства V известен как проективное пространство ; его можно использовать для формализации идеи параллельных линий, пересекающихся на бесконечности. Грассманианы и многообразия флагов обобщают это путем параметризации линейных подпространств фиксированной размерности k и флагов подпространств соответственно.

Ссылки

Алгебра

• Антон, Ховард; Роррес, Крис (2010), Элементарная линейная алгебра: версия приложений (10-е изд.), John Wiley & Sons
• Артин, Майкл (1991), Алгебра , Прентис Холл , ISBN  978-0-89871-510-1
• Браун, Уильям А. (1991), Матрицы и векторные пространства , Нью-Йорк: М. Деккер, ISBN  978-0-8247-8419-5
• Грилле, Пьер Антуан (2007), Абстрактная алгебра , том. 242, Springer Science & Business Media, номер домена : 10.1007/978-0-387-71568-1 , ISBN.  978-0-387-71568-1
• Халмош, Пол Р. (1948), Конечномерные векторные пространства , том. 7, Издательство Принстонского университета
• Хайль, Кристофер (2011), Учебник по базовой теории: расширенное издание , Прикладной и численный гармонический анализ, Биркхойзер, номер документа : 10.1007/978-0-8176-4687-5 , ISBN  978-0-8176-4687-5
• Джайн, MC (2001), Векторные пространства и матрицы в физике , CRC Press, ISBN  978-0-8493-0978-6
• Джоши, К.Д. (1989), Основы дискретной математики , John Wiley & Sons
• Крейциг, Эрвин (2020), Высшая инженерная математика , John Wiley & Sons, ISBN  978-1-119-45592-9
• Ланг, Серж (1987), Линейная алгебра , Тексты для бакалавров по математике (3-е изд.), Springer, doi : 10.1007/978-1-4757-1949-9 , ISBN  978-1-4757-1949-9
• Ланг, Серж (2002), Алгебра , Тексты для выпускников по математике , том. 211 (пересмотренное третье издание), Нью-Йорк: Springer-Verlag, ISBN.  978-0-387-95385-4 , МР   1878556
• Мак Лейн, Сондерс (1999), Алгебра (3-е изд.), American Mathematical Soc. стр. 193–222, ISBN.  978-0-8218-1646-2
• Мейер, Карл Д. (2000), Матричный анализ и прикладная линейная алгебра , SIAM , ISBN  978-0-89871-454-8
• Николсон, В. Кейт (2018), Линейная алгебра с приложениями , Lyryx
• Роман, Стивен (2005), Продвинутая линейная алгебра , Тексты для выпускников по математике, том. 135 (2-е изд.), Берлин, Нью-Йорк: Springer-Verlag , ISBN  978-0-387-24766-3
• Шпиндлер, Карлхайнц (1993), Абстрактная алгебра с приложениями: Том 1: Векторные пространства и группы , CRC, ISBN  978-0-8247-9144-5
• Спрингер, Т. А. (2000), Линейные алгебраические группы , Спрингер, ISBN  978-0-8176-4840-4
• Столл, РР; Вонг, ET (1968), Линейная алгебра , Academic Press
• ван дер Варден, Бартель Леендерт (1993), Алгебра (на немецком языке) (9-е изд.), Берлин, Нью-Йорк: Springer-Verlag , ISBN  978-3-540-56799-8

Анализ

• Бурбаки, Николя (1987), Топологические векторные пространства , Элементы математики, Берлин, Нью-Йорк: Springer-Verlag , ISBN  978-3-540-13627-9
• Бурбаки, Николя (2004), Интеграция I , Берлин, Нью-Йорк: Springer-Verlag , ISBN  978-3-540-41129-1
• Браун, Мартин (1993), Дифференциальные уравнения и их приложения: введение в прикладную математику , Берлин, Нью-Йорк: Springer-Verlag , ISBN  978-0-387-97894-9
• BSE-3 (2001) [1994], «Касательная плоскость» , Энциклопедия Математики , EMS Press
• Шоке, Гюстав (1966), Топология , Бостон, Массачусетс: Academic Press
• Деннери, Филипп; Крживицкий, Андре (1996), Математика для физиков , Courier Dover Publications, ISBN  978-0-486-69193-0
• Дадли, Ричард М. (1989), Реальный анализ и вероятность , Серия математики Уодсворта и Брукса/Коула, Пасифик Гроув, Калифорния: Wadsworth & Brooks/Cole Advanced Books & Software, ISBN  978-0-534-10050-6
• Данэм, Уильям (2005), Галерея исчисления , Princeton University Press , ISBN  978-0-691-09565-3
• Эванс, Лоуренс К. (1998), Уравнения в частных производных , Провиденс, Род-Айленд: Американское математическое общество , ISBN  978-0-8218-0772-9
• Фолланд, Джеральд Б. (1992), Анализ Фурье и его приложения , Брукс-Коул, ISBN  978-0-534-17094-3
• Гаске, Клод; Витомски, Патрик (1999), Анализ Фурье и приложения: фильтрация, численные вычисления, вейвлеты , тексты по прикладной математике, Нью-Йорк: Springer-Verlag, ISBN  978-0-387-98485-8
• Ифичор, Эммануэль К.; Джервис, Барри В. (2001), Цифровая обработка сигналов: практический подход (2-е изд.), Харлоу, Эссекс, Англия: Прентис-Холл (опубликовано в 2002 г.), ISBN  978-0-201-59619-9
• Кранц, Стивен Г. (1999), Панорама гармонического анализа , Математические монографии Каруса, Вашингтон, округ Колумбия: Математическая ассоциация Америки, ISBN  978-0-88385-031-2
• Крейциг, Эрвин (1988), Высшая инженерная математика (6-е изд.), Нью-Йорк: John Wiley & Sons, ISBN  978-0-471-85824-9
• Крейциг, Эрвин (1989), Вводный функциональный анализ с приложениями , Wiley Classics Library, Нью-Йорк: John Wiley & Sons , ISBN  978-0-471-50459-7 , МР   0992618
• Ланг, Серж (1983), Реальный анализ , Аддисон-Уэсли , ISBN  978-0-201-14179-5
• Ланг, Серж (1993), Реальный и функциональный анализ , Берлин, Нью-Йорк: Springer-Verlag , ISBN  978-0-387-94001-4
• Лумис, Линн Х. (2011) [1953], Введение в абстрактный гармонический анализ , Дувр, hdl : 2027/uc1.b4250788 , ISBN  978-0-486-48123-4 , OCLC   702357363
• Наричи, Лоуренс; Бекенштейн, Эдвард (2011). Топологические векторные пространства . Чистая и прикладная математика (Второе изд.). Бока-Ратон, Флорида: CRC Press. ISBN  978-1584888666 . OCLC   144216834 .
• Рудин, Уолтер (1991), Функциональный анализ (2-е изд.), McGraw-Hill, ISBN  0070542368
• Шефер, Хельмут Х .; Вольф, Манфред П. (1999). Топологические векторные пространства . ГТМ . Том. 8 (Второе изд.). Нью-Йорк, Нью-Йорк: Springer New York Выходные данные Springer. ISBN  978-1-4612-7155-0 . OCLC   840278135 .
• Тревес, Франсуа (1967), Топологические векторные пространства, распределения и ядра , Бостон, Массачусетс: Academic Press

Исторические справки

• Банах, Стефан (1922), «Об операциях в абстрактных множествах и их применении к интегральным уравнениям» (PDF) , Fundamenta Mathematicae (на французском языке), 3 : 133–181, doi : 10.4064/fm-3-1-133- 181 , ISSN   0016-2736
• Больцано, Бернар (1804 г.), Размышления о некоторых аспектах элементарной геометрии (на немецком языке)
• Беллавитис, Джузо (1833), «О некоторых приложениях нового метода аналитической геометрии», Il poligrafo Journal di Scienze, Lettre ed Arti , 13 , Верона: 53–61 .
• Бурбаки, Николя (1969), Элементы истории математики (на французском языке), Париж: Герман
• Дорье, Жан-Люк (1995), «Общий очерк возникновения теории векторного пространства» , Historia Mathematica , 22 (3): 227–261, doi : 10.1006/hmat.1995.1024 , MR   1347828
• Фурье, Жан Батист Жозеф (1822), Аналитическая теория тепла (на французском языке), Ше Фирмен Дидо, отец и сын
• Грассманн, Герман (1844), Теория линейного расширения - новая ветвь математики (на немецком языке), О. Виганд , переиздание: Грассманн, Герман (2000), Канненберг, LC (редактор), Теория расширения , перевод Канненберга, Ллойда К., Провиденс, Род-Айленд: Американское математическое общество , ISBN  978-0-8218-2031-5
• Го, Хунъюй (16 июня 2021 г.), Что такое тензоры? , Всемирный научный, ISBN  978-981-12-4103-1
• Гамильтон, Уильям Роуэн (1853), Лекции по кватернионам , Королевская ирландская академия
• Мёбиус, Август Фердинанд (1827 г.), Барицентрическое исчисление: новая утилита для аналитической обработки геометрии ( на немецком языке), заархивировано из оригинала 23 ноября 2006 г.
• Мур, Грегори Х. (1995), «Аксиоматизация линейной алгебры: 1875–1940», Historia Mathematica , 22 (3): 262–303, doi : 10.1006/hmat.1995.1025
• Пеано, Джузеппе (1888), Геометрическое исчисление в соответствии с Ausdehnungslehre Х. Грассмана, которому предшествуют операции дедуктивной логики (на итальянском языке), Турин {{citation}}: CS1 maint: отсутствует местоположение издателя ( ссылка )
• Пеано, Г. (1901) Formulario mathematico : аксиомы vct, через Интернет-архив

Дальнейшие ссылки

• Эшкрофт, Нил ; Мермин, Н. Дэвид (1976), Физика твердого тела , Торонто: Thomson Learning, ISBN  978-0-03-083993-1
• Атья, Майкл Фрэнсис (1989), K-теория , Advanced Book Classics (2-е изд.), Аддисон-Уэсли , ISBN  978-0-201-09394-0 , МР   1043170
• Атья, Майкл Фрэнсис ; Макдональд, Ян Грант (1969), Введение в коммутативную алгебру , Advanced Book Classics, Аддисон-Уэсли
• Бласс, Андреас (1984), «Существование базисов подразумевает аксиому выбора» (PDF) , Аксиоматическая теория множеств , Современная математика, том 31, Провиденс, Род-Айленд: Американское математическое общество , стр. 31–33, ISBN  978-0-8218-5026-8 , МР   0763890
• Бурбаки, Николя (1998), Элементы математики: Алгебра I, главы 1–3 , Берлин, Нью-Йорк: Springer-Verlag , ISBN  978-3-540-64243-5
• Бурбаки, Николас (1989), Общая топология. Главы 1–4 , Берлин, Нью-Йорк: Издательство Springer , ISBN  978-3-540-64241-1
• Коксетер, Гарольд Скотт Макдональд (1987), Проективная геометрия (2-е изд.), Берлин, Нью-Йорк: Springer-Verlag , ISBN  978-0-387-96532-1
• Айзенберг, Мюррей; Гай, Роберт (1979), «Доказательство теоремы о волосатом шаре», The American Mathematical Monthly , 86 (7): 572–574, doi : 10.2307/2320587 , JSTOR   2320587
• Эйзенбуд, Дэвид (1995), Коммутативная алгебра , Тексты для выпускников по математике, том. 150, Берлин, Нью-Йорк: Springer-Verlag , ISBN.  978-0-387-94269-8 , МР   1322960
• Голдрей, Дерек (1996), Классическая теория множеств: независимое исследование под руководством руководства (1-е изд.), Лондон: Чепмен и Холл , ISBN  978-0-412-60610-6
• Гриффитс, Дэвид Дж. (1995), Введение в квантовую механику , Аппер-Сэддл-Ривер, Нью-Джерси: Прентис-Холл , ISBN  978-0-13-124405-4
• Халмош, Пол Р. (1974), Конечномерные векторные пространства , Берлин, Нью-Йорк: Springer-Verlag , ISBN  978-0-387-90093-3
• Халперн, Джеймс Д. (июнь 1966 г.), «Базы в векторных пространствах и аксиома выбора», Proceedings of the American Mathematical Society , 17 (3): 670–673, doi : 10.2307/2035388 , JSTOR   2035388
• Хьюз-Халлетт, Дебора; МакКаллум, Уильям Г.; Глисон, Эндрю М. (2013), Исчисление: одномерные и многомерные (6-е изд.), John Wiley & Sons , ISBN  978-0470-88861-2
• Хуземоллер, Дейл (1994), Fiber Bundles (3-е изд.), Берлин, Нью-Йорк: Springer-Verlag , ISBN  978-0-387-94087-8
• Йост, Юрген (2005), Риманова геометрия и геометрический анализ (4-е изд.), Берлин, Нью-Йорк: Springer-Verlag , ISBN  978-3-540-25907-7
• Крейциг, Эрвин (1991), Дифференциальная геометрия , Нью-Йорк: Dover Publications , стр. xiv+352, ISBN  978-0-486-66721-8
• Крейциг, Эрвин (1999), Высшая инженерная математика (8-е изд.), Нью-Йорк: John Wiley & Sons , ISBN  978-0-471-15496-9
• Люенбергер, Дэвид (1997), Оптимизация методами векторного пространства , Нью-Йорк: John Wiley & Sons , ISBN  978-0-471-18117-0
• Мак Лейн, Сондерс (1998), Категории для работающего математика (2-е изд.), Берлин, Нью-Йорк: Springer-Verlag , ISBN  978-0-387-98403-2
• Миснер, Чарльз В .; Торн, Кип ; Уилер, Джон Арчибальд (1973), Гравитация , WH Freeman, ISBN  978-0-7167-0344-0
• Набер, Грегори Л. (2003), Геометрия пространства-времени Минковского , Нью-Йорк: Dover Publications , ISBN  978-0-486-43235-9 , МР   2044239
• Шенхаге, А .; Штрассен, Волкер (1971), «Быстрое умножение больших чисел», Computing (на немецком языке), 7 (3–4): 281–292, doi : 10.1007/bf02242355 , ISSN   0010-485X , S2CID   9738629
• Спивак, Майкл (1999), Всеобъемлющее введение в дифференциальную геометрию (том второй) , Хьюстон, Техас: опубликуй или погибни
• Стюарт, Ян (1975), Теория Галуа , Чепмена и Холла Серия математики , Лондон: Чепмен и Холл , ISBN  978-0-412-10800-6
• Варадараджан, В.С. (1974), Группы Ли, алгебры Ли и их представления , Прентис Холл , ISBN  978-0-13-535732-3
• Уоллес, Г.К. (февраль 1992 г.), «Стандарт сжатия неподвижных изображений JPEG» (PDF) , IEEE Transactions on Consumer Electronics , 38 (1): xviii–xxxiv, CiteSeerX   10.1.1.318.4292 , doi : 10.1109/30.125072 , ISSN   0098 -3063 , заархивировано из оригинала (PDF) 13 января 2007 г. , получено 25 октября 2017 г.
• Вейбель, Чарльз А. (1994). Введение в гомологическую алгебру . Кембриджские исследования по высшей математике. Том. 38. Издательство Кембриджского университета. ISBN  978-0-521-55987-4 . МР   1269324 . OCLC   36131259 .

Внешние ссылки

• «Векторное пространство» , Математическая энциклопедия , EMS Press , 2001 [1994]