Внешняя алгебра

«Продукт клина» перенаправляется сюда. Для работы с топологическими пространствами см. Сумма клина .

Ориентация определяется упорядоченным набором векторов.

Обратная ориентация соответствует отрицанию внешнего продукта.

Геометрическая интерпретация элементов степени n в реальной внешней алгебре для n = 0 (точка со знаком), 1 (направленный отрезок или вектор), 2 (ориентированный плоский элемент), 3 (ориентированный объем). Внешний продукт n векторов можно визуализировать как любую n -мерную форму (например, n - параллелотоп , n - эллипсоид ); с величиной ( гиперобъемом ) и ориентацией , определяемой ориентацией его ( n - 1) -мерной границы и тем, на какой стороне находится внутренняя часть.

В математике — внешняя алгебра или алгебра Грассмана векторного пространства. $V$ является ассоциативной алгеброй , содержащей $V,$ который имеет продукт, называемый внешним продуктом или клиновым продуктом и обозначаемый $\wedge$, такой, что $v\wedge v=0$ для каждого вектора $v$ в $V.$ Внешняя алгебра названа в честь Германа Грассмана . а названия продукта произошли от символа «клин». $\wedge$ и тот факт, что произведение двух элементов $V$ находятся «снаружи» $V.$

Клиновое произведение $k$ векторы $v_{1}\wedge v_{2}\wedge \dots \wedge v_{k}$ называется лезвием степени ​ $k$ или $k$- лезвие . Произведение клина было первоначально введено как алгебраическая конструкция, используемая в геометрии для изучения площадей , объемов и их многомерных аналогов: Величина лопастного 2 - $v\wedge w$ - площадь параллелограмма, определяемая формулой $v$ и $w,$ и, в более общем плане, величина $k$-лопасть — это (гипер)объем параллелоэдра, определяемый составляющими его векторами. Переменное свойство , которое $v\wedge v=0$ подразумевает кососимметричное свойство, которое $v\wedge w=-w\wedge v,$ и, в более общем смысле, любое лезвие меняет знак всякий раз, когда два составляющих его вектора меняются местами, что соответствует параллелоэдру противоположной ориентации.

Полная внешняя алгебра содержит объекты, которые сами по себе не являются лезвиями, а являются линейными комбинациями лезвий; сумма лопастей однородной степени $k$ называется k - вектором , а более общая сумма лопастей произвольной степени называется мультивектором . Линейный размах ​ $k$-лезвия называется $k$- внешняя сила $V.$ Внешняя алгебра представляет собой прямую сумму $k$-ые внешние силы $V,$ и это делает внешнюю алгебру градуированной алгеброй .

Внешняя алгебра универсальна в том смысле, что каждое уравнение, связывающее элементы $V$ во внешней алгебре справедливо также во всякой ассоциативной алгебре, содержащей $V$ и в котором квадрат каждого элемента $V$ равен нулю.

Определение внешней алгебры может быть расширено для пространств, построенных из векторных пространств, таких как векторные поля и функции которых , областью определения является векторное пространство. При этом поле скаляров может быть любым полем (однако для полей характеристики два вышеприведенное условие $v\wedge v=0$ необходимо заменить на $v\wedge w+w\wedge v=0,$что эквивалентно по остальным характеристикам). В более общем смысле внешняя алгебра может быть определена для модулей над коммутативным кольцом . В частности, алгебра дифференциальных форм в $k$ переменных является внешней алгеброй над кольцом гладких функций в $k$ переменные.

Мотивирующие примеры

Области в плоскости

Площадь параллелограмма через определитель матрицы координат двух его вершин.

Двумерное евклидово векторное пространство $\mathbf {R} ^{2}$ — вещественное векторное пространство, снабженное базисом , состоящим из пары ортогональных единичных векторов

${\mathbf {e} }_{1}={\begin{bmatrix}1\\0\end{bmatrix}},\quad {\mathbf {e} }_{2}={\begin{bmatrix}0\\1\end{bmatrix}}.$

Предположим, что

$\mathbf {v} ={\begin{bmatrix}a\\b\end{bmatrix}}=a\mathbf {e} _{1}+b\mathbf {e} _{2},\quad \mathbf {w} ={\begin{bmatrix}c\\d\end{bmatrix}}=c\mathbf {e} _{1}+d\mathbf {e} _{2}$

представляют собой пару заданных векторов в $\mathbf {R} ^{2}$, записанный в компонентах. Существует единственный параллелограмм, имеющий $\mathbf {v}$ и $\mathbf {w}$как две его стороны. Площадь этого параллелограмма определяется стандартной формулой определителя :

${\text{Area}}={\Bigl |}\det {\begin{bmatrix}\mathbf {v} &\mathbf {w} \end{bmatrix}}{\Bigr |}={\Biggl |}\det {\begin{bmatrix}a&c\\b&d\end{bmatrix}}{\Biggr |}=\left|ad-bc\right|.$

Рассмотрим теперь внешнее произведение $\mathbf {v}$ и $\mathbf {w}$:

${\begin{aligned}\mathbf {v} \wedge \mathbf {w} &=(a\mathbf {e} _{1}+b\mathbf {e} _{2})\wedge (c\mathbf {e} _{1}+d\mathbf {e} _{2})\\&=ac\mathbf {e} _{1}\wedge \mathbf {e} _{1}+ad\mathbf {e} _{1}\wedge \mathbf {e} _{2}+bc\mathbf {e} _{2}\wedge \mathbf {e} _{1}+bd\mathbf {e} _{2}\wedge \mathbf {e} _{2}\\&=\left(ad-bc\right)\mathbf {e} _{1}\wedge \mathbf {e} _{2}\end{aligned}}$

где на первом этапе используется закон распределения внешнего продукта , а на последнем — тот факт, что внешний продукт представляет собой знакопеременное отображение , и, в частности, $\mathbf {e} _{2}\wedge \mathbf {e} _{1}=-(\mathbf {e} _{1}\wedge \mathbf {e} _{2}).$ (Тот факт, что внешний продукт представляет собой чередующуюся карту, также заставляет $\mathbf {e} _{1}\wedge \mathbf {e} _{1}=\mathbf {e} _{2}\wedge \mathbf {e} _{2}=0.$) Обратите внимание, что коэффициент в этом последнем выражении является в точности определителем матрицы [ v w ] . Тот факт, что это может быть положительным или отрицательным, имеет интуитивное значение, заключающееся в том, что v и w могут быть ориентированы по часовой стрелке или против часовой стрелки, как вершины параллелограмма, который они определяют. Такая площадь называется знаковой площадью параллелограмма: абсолютное значение знаковой площади — это обычная площадь, а знак определяет ее ориентацию.

Тот факт, что этот коэффициент является знаковой областью, не случаен. Фактически, относительно легко увидеть, что внешний продукт должен быть связан со знаковой областью, если попытаться аксиоматизировать эту область как алгебраическую конструкцию. Подробно, если A( v , w ) обозначает область параллелограмма со знаком, в котором пара векторов v и w образует две смежные стороны, то A должен удовлетворять следующим свойствам:

1. A( r v , s w ) = rs A( v , w ) для любых действительных чисел r и s , поскольку изменение масштаба любой из сторон изменяет масштаб площади на ту же величину (а изменение направления одной из сторон меняет ориентацию на противоположную) параллелограмма).
2. A( v , v ) = 0 , поскольку площадь вырожденного параллелограмма, определяемого v (т. е. отрезок прямой ), равна нулю.
3. A( w , v ) = −A( v , w ) , поскольку замена ролей v и w меняет ориентацию параллелограмма на противоположную.
4. A( v + r w , w ) = A( v , w ) для любого действительного числа r , поскольку добавление кратного w к v не влияет ни на основание, ни на высоту параллелограмма и, следовательно, сохраняет его площадь.
5. A( e ₁ , e ₂ ) = 1 , поскольку площадь единичного квадрата равна единице.

Перекрестное произведение ( синий вектор) по отношению к внешнему произведению ( голубой параллелограмм). Длина векторного произведения равна длине параллельного единичного вектора ( красный ), а размер внешнего произведения соответствует размеру эталонного параллелограмма ( светло-красный ).

За исключением последнего свойства, внешнее произведение двух векторов обладает теми же свойствами, что и площадь. В определенном смысле внешний продукт обобщает окончательное свойство, позволяя сравнивать площадь параллелограмма с площадью любого выбранного параллелограмма в параллельной плоскости (в данном случае со сторонами e ₁ и e ₂ ). Другими словами, внешний продукт обеспечивает независимую от базиса формулировку площади.

Перекрестные и тройные произведения

Для векторов в R ³ внешняя алгебра тесно связана с векторным произведением и тройным произведением . Используя стандартный базис { e ₁ , e ₂ , e ₃ } , внешнее произведение пары векторов

$\mathbf {u} =u_{1}\mathbf {e} _{1}+u_{2}\mathbf {e} _{2}+u_{3}\mathbf {e} _{3}$

и

$\mathbf {v} =v_{1}\mathbf {e} _{1}+v_{2}\mathbf {e} _{2}+v_{3}\mathbf {e} _{3}$

является

$\mathbf {u} \wedge \mathbf {v} =(u_{1}v_{2}-u_{2}v_{1})(\mathbf {e} _{1}\wedge \mathbf {e} _{2})+(u_{3}v_{1}-u_{1}v_{3})(\mathbf {e} _{3}\wedge \mathbf {e} _{1})+(u_{2}v_{3}-u_{3}v_{2})(\mathbf {e} _{2}\wedge \mathbf {e} _{3})$

где { e ₁ ∧ e ₂ , e ₃ ∧ e _​​1 , e ₂ ∧ e ₃ } — основа трехмерного пространства ⋀ ² ( Р ³ ). Приведенные выше коэффициенты такие же, как и в обычном определении векторного произведения векторов в трех измерениях, с той лишь разницей, что внешнее произведение не является обычным вектором, а является бивектором .

Вводим третий вектор

$\mathbf {w} =w_{1}\mathbf {e} _{1}+w_{2}\mathbf {e} _{2}+w_{3}\mathbf {e} _{3},$

внешнее произведение трех векторов равно

$\mathbf {u} \wedge \mathbf {v} \wedge \mathbf {w} =(u_{1}v_{2}w_{3}+u_{2}v_{3}w_{1}+u_{3}v_{1}w_{2}-u_{1}v_{3}w_{2}-u_{2}v_{1}w_{3}-u_{3}v_{2}w_{1})(\mathbf {e} _{1}\wedge \mathbf {e} _{2}\wedge \mathbf {e} _{3})$

где e ₁ ∧ e ₂ ∧ e ₃ — базисный вектор одномерного пространства ⋀ ³ ( Р ³ ). Скалярный коэффициент представляет собой тройное произведение трех векторов.

Перекрестное произведение и тройное произведение в трех измерениях допускают как геометрическую, так и алгебраическую интерпретацию. Векторное произведение u × v можно интерпретировать как вектор, который перпендикулярен как u , так и v и величина которого равна площади параллелограмма, определяемого двумя векторами. Его также можно интерпретировать как вектор, состоящий из миноров матрицы со столбцами u и v . Тройное произведение u , v и w геометрически является (подписанным) объемом. Алгебраически это определитель матрицы со столбцами u , v и w . Внешний вид изделия в трех измерениях допускает аналогичные интерпретации. Фактически, при наличии положительно ориентированного ортонормированного базиса внешнее произведение обобщает эти понятия на более высокие измерения.

Формальное определение

Внешняя алгебра $\bigwedge (V)$ векторного пространства $V$ над полем $K$ определяется как факторалгебра тензорной алгебры по двустороннему идеалу $I$ генерируется всеми элементами формы $x\otimes x$ такой, что $x\in V$. Символически,

$\bigwedge (V):=T(V)/I.\,$

Внешний вид продукта $\wedge$ из двух элементов $\bigwedge (V)$ определяется

$\alpha \wedge \beta =\alpha \otimes \beta {\pmod {I}}.$

Алгебраические свойства

Альтернативный продукт

Внешнее изделие представляет собой конструкцию, чередующуюся из элементов $V$, Который означает, что $x\wedge x=0$ для всех $x\in V,$по вышеуказанной конструкции. Отсюда следует, что произведение также антикоммутативно на элементах $V$, за предположение, что $x,y\in V$,

$0=(x+y)\wedge (x+y)=x\wedge x+x\wedge y+y\wedge x+y\wedge y=x\wedge y+y\wedge x$

следовательно

$x\wedge y=-(y\wedge x).$

В более общем смысле, если $\sigma$ является перестановкой целых чисел $[1,\dots ,k]$, и $x_{1}$, $x_{2}$, ..., $x_{k}$ являются элементами $V$, следует, что

$x_{\sigma (1)}\wedge x_{\sigma (2)}\wedge \cdots \wedge x_{\sigma (k)}=\operatorname {sgn}(\sigma )x_{1}\wedge x_{2}\wedge \cdots \wedge x_{k},$

где $\operatorname {sgn}(\sigma )$ это подпись перестановки $\sigma$.

В частности, если $x_{i}=x_{j}$ для некоторых $i\neq j$, то имеет место также следующее обобщение знакопеременного свойства:

$x_{1}\wedge x_{2}\wedge \cdots \wedge x_{k}=0.$

Вместе с распределительным свойством внешнего продукта еще одно обобщение состоит в том, что необходимым и достаточным условием для $\{x_{1},x_{2},\dots ,x_{k}\}$ быть линейно зависимым набором векторов состоит в том, что

$x_{1}\wedge x_{2}\wedge \cdots \wedge x_{k}=0.$

Внешняя мощность

k я - внешняя степень $V$, обозначенный ${\textstyle \bigwedge }^{\!k}(V)$, — подпространство векторное ${\textstyle \bigwedge }(V)$ состоит из элементов формы

$x_{1}\wedge x_{2}\wedge \cdots \wedge x_{k},\quad x_{i}\in V,i=1,2,\dots ,k.$

Если $\alpha \in {\textstyle \bigwedge }^{\!k}(V)$, затем $\alpha$называется k -вектором . Если, кроме того, $\alpha$ можно выразить как внешний продукт $k$ элементы $V$, затем $\alpha$называется разложимым ( или простым , по мнению некоторых авторов, или лезвием , по мнению других). Хотя и разложимый $k$-диапазон векторов ${\textstyle \bigwedge }^{\!k}(V)$, не каждый элемент ${\textstyle \bigwedge }^{\!k}(V)$является разложимым. Например, учитывая $\mathbf {R} ^{4}$ с основой $\{e_{1},e_{2},e_{3},e_{4}\}$, следующий 2-вектор неразложим:

$\alpha =e_{1}\wedge e_{2}+e_{3}\wedge e_{4}.$

Основа и размерность

Если размерность ​ $V$ является $n$ и $\{e_{1},\dots ,e_{n}\}$ является основой для $V$, то набор

$\{\,e_{i_{1}}\wedge e_{i_{2}}\wedge \cdots \wedge e_{i_{k}}~{\big |}~~1\leq i_{1}<i_{2}<\cdots <i_{k}\leq n\,\}$

является основой для ${\textstyle \bigwedge }^{\!k}(V)$. Причина в следующем: дано любое внешнее произведение вида

$v_{1}\wedge \cdots \wedge v_{k},$

каждый вектор $v_{j}$ можно записать как линейную комбинацию базисных векторов $e_{i}$; используя билинейность внешнего произведения, это можно расширить до линейной комбинации внешних произведений этих базисных векторов. Любой внешний продукт, в котором один и тот же базисный вектор встречается более одного раза, равен нулю; любой внешний продукт, в котором базисные векторы не расположены в правильном порядке, можно переупорядочить, меняя знак всякий раз, когда два базисных вектора меняются местами. В общем, результирующие коэффициенты базисных k -векторов можно вычислить как миноры матрицы , описывающей векторы $v_{j}$ с точки зрения основы $e_{i}$.

Подсчитав базисные элементы, размерность ${\textstyle \bigwedge }^{\!k}(V)$ равен биномиальному коэффициенту :

$\dim {\textstyle \bigwedge }^{\!k}(V)={\binom {n}{k}},$

где $n$ - размерность векторов , а $k$— количество векторов в произведении. Биномиальный коэффициент дает правильный результат даже в исключительных случаях; в частности, ${\textstyle \bigwedge }^{\!k}(V)=\{0\}$ для $k>n$.

Любой элемент внешней алгебры можно записать в виде суммы k -векторов . Следовательно, как векторное пространство внешняя алгебра представляет собой прямую сумму

${\textstyle \bigwedge }(V)={\textstyle \bigwedge }^{\!0}(V)\oplus {\textstyle \bigwedge }^{\!1}(V)\oplus {\textstyle \bigwedge }^{\!2}(V)\oplus \cdots \oplus {\textstyle \bigwedge }^{\!n}(V)$

(где по соглашению ${\textstyle \bigwedge }^{\!0}(V)=K$, поле , лежащее в основе $V$, и ${\textstyle \bigwedge }^{\!1}(V)=V$), и поэтому его размерность равна сумме биномиальных коэффициентов, что составляет $2^{n}$.

Ранг k -вектора

Если $\alpha \in {\textstyle \bigwedge }^{\!k}(V)$, то можно выразить $\alpha$ как линейную комбинацию разложимых k -векторов :

$\alpha =\alpha ^{(1)}+\alpha ^{(2)}+\cdots +\alpha ^{(s)}$

где каждый $\alpha ^{(i)}$ разложимо, скажем

$\alpha ^{(i)}=\alpha _{1}^{(i)}\wedge \cdots \wedge \alpha _{k}^{(i)},\quad i=1,2,\ldots ,s.$

Ранг ​ k -вектора ​ $\alpha$ — минимальное число разложимых k -векторов в таком разложении $\alpha$. Это похоже на понятие тензорного ранга .

Ранг особенно важен при изучении 2-векторов ( Sternberg 1964 , §III.6) ( Bryant et al. 1991 ). Ранг 2-вектора $\alpha$ можно отождествить с половиной ранга матрицы коэффициентов $\alpha$в основе. Таким образом, если $e_{i}$ является основой для $V$, затем $\alpha$ может быть выражено однозначно как

$\alpha =\sum _{i,j}a_{ij}e_{i}\wedge e_{j}$

где $a_{ij}=-a_{ji}$(матрица коэффициентов кососимметрична ). Ранг матрицы $a_{ij}$ поэтому четно и в два раза выше ранга формы $\alpha$.

В характеристике 0 2-вектор $\alpha$ имеет ранг $p$ если и только если

${\underset {p}{\underbrace {\alpha \wedge \cdots \wedge \alpha } }}\neq 0\$ и $\ {\underset {p+1}{\underbrace {\alpha \wedge \cdots \wedge \alpha } }}=0.$

структура

Внешнее произведение k -вектора на p -вектор - это $(k+p)$-вектор, еще раз ссылаясь на билинейность. Как следствие, разложение в прямую сумму предыдущего раздела

${\textstyle \bigwedge }(V)={\textstyle \bigwedge }^{\!0}(V)\oplus {\textstyle \bigwedge }^{\!1}(V)\oplus {\textstyle \bigwedge }^{\!2}(V)\oplus \cdots \oplus {\textstyle \bigwedge }^{\!n}(V)$

придает внешней алгебре дополнительную структуру градуированной алгебры , т.е.

${\textstyle \bigwedge }^{\!k}(V)\wedge {\textstyle \bigwedge }^{\!p}(V)\subset {\textstyle \bigwedge }^{\!k+p}(V).$

Более того, если K — базовое поле, мы имеем

${\textstyle \bigwedge }^{\!0}(V)=K$ и ${\textstyle \bigwedge }^{\!1}(V)=V.$

Внешний продукт оценивается как антикоммутативный, что означает, что если $\alpha \in {\textstyle \bigwedge }^{\!k}(V)$ и $\beta \in {\textstyle \bigwedge }^{\!p}(V)$, затем

$\alpha \wedge \beta =(-1)^{kp}\beta \wedge \alpha .$

Помимо изучения градуированной структуры внешней алгебры, Бурбаки (1989) изучает дополнительные градуированные структуры внешних алгебр, например структуры внешней алгебры градуированного модуля (модуля, который уже несет свою собственную градуировку).

Универсальная собственность

Пусть V векторное пространство над полем K. — Неформально, умножение в ${\textstyle \bigwedge }(V)$ осуществляется путем манипулирования символами и наложения закона распределения , ассоциативного закона и использования тождества $v\wedge v=0$для v ∈ V . Формально, ${\textstyle \bigwedge }(V)$ является «наиболее общей» алгеброй, в которой эти правила выполняются для умножения, в том смысле, что любая ассоциативная K -алгебра с единицей, содержащая V с попеременным умножением на V , должна содержать гомоморфный образ ${\textstyle \bigwedge }(V)$. Другими словами, внешняя алгебра обладает следующим универсальным свойством :

Для любой ассоциативной K -алгебры A с единицей и любого K - линейного отображения $j:V\to A$ такой, что $j(v)j(v)=0$ для каждого v из V существует ровно один с единицей гомоморфизм алгебры $f:{\textstyle \bigwedge }(V)\to A$ такой, что j ( v ) = f ( i ( v )) для всех v в V (здесь i — естественное включение V в ${\textstyle \bigwedge }(V)$, см. выше).

Universal property of the exterior algebra

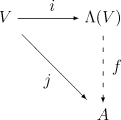
Чтобы построить наиболее общую алгебру, содержащую V и умножение которой является попеременным на V , естественно начать с наиболее общей ассоциативной алгебры, содержащей V , тензорной алгебры T ( V ) , а затем обеспечить соблюдение знакопеременного свойства, взяв подходящую частное . Таким образом, мы берем двусторонний идеал I в T ( V ) , порожденный всеми элементами формы v ⊗ v для v в V , и определяем ${\textstyle \bigwedge }(V)$ как частное

${\textstyle \bigwedge }(V)=T(V)\,/\,I$

(и используйте ∧ как символ умножения в ${\textstyle \bigwedge }(V)$). Тогда несложно показать, что ${\textstyle \bigwedge }(V)$ содержит V и удовлетворяет указанному выше универсальному свойству.

Как следствие этой конструкции, операция присвоения векторному пространству V его внешней алгебры ${\textstyle \bigwedge }(V)$ является функтором из категории векторных пространств в категорию алгебр.

Вместо того, чтобы определять ${\textstyle \bigwedge }(V)$ сначала, а затем выявление внешних сил ${\textstyle \bigwedge }^{\!k}(V)$ как определенные подпространства, можно альтернативно определить пространства ${\textstyle \bigwedge }^{\!k}(V)$ сначала, а затем объединить их в алгебру ${\textstyle \bigwedge }(V)$. Этот подход часто используется в дифференциальной геометрии и описан в следующем разделе.

Обобщения

Учитывая коммутативное кольцо $R$ и $R$- модуль $M$, мы можем определить внешнюю алгебру ${\textstyle \bigwedge }(M)$ как и выше, в качестве подходящего фактора тензорной алгебры $\mathrm {T} (M)$. Оно будет удовлетворять аналогичному универсальному свойству. Многие свойства ${\textstyle \bigwedge }(M)$ также требуют, чтобы $M$быть проективным модулем . Если используется конечная размерность, свойства дополнительно требуют, чтобы $M$быть конечно порожденным и проективным. Обобщения наиболее распространенных ситуаций можно найти у Бурбаки (1989) .

Внешние алгебры векторных расслоений часто рассматриваются в геометрии и топологии. нет существенных различий между алгебраическими свойствами внешней алгебры конечномерных векторных расслоений и свойствами внешней алгебры конечно порожденных проективных модулей По теореме Серра – Свона . Более общие внешние алгебры могут быть определены для пучков модулей.

тензорная

Для поля характеристики не 2, внешняя алгебра векторного пространства $V$ над $K$ канонически можно отождествить с векторным подпространством $\mathrm {T} (V)$состоящее из антисимметричных тензоров . Для характеристики 0 (или выше $\dim V$), векторное пространство $k$-линейный антисимметричный тензор трансверсален идеалу $I$, следовательно, хороший выбор для представления частного. Но для ненулевой характеристики векторное пространство $K$-линейные антисимметричные тензоры могут быть не трансверсальны идеальному (фактически, для $k\geq \operatorname {char} K$, векторное пространство $K$-линейные антисимметричные тензоры содержатся в $I$); тем не менее, трансверсально или нет, произведение может быть определено в этом пространстве так, что результирующая алгебра будет изоморфна внешней алгебре: в первом случае естественным выбором для произведения является просто факторпроизведение (с использованием доступной проекции), в во втором случае это произведение должно быть слегка изменено, как указано ниже (в соответствии с установкой Арнольда), но так, чтобы алгебра оставалась изоморфной внешней алгебре, т. е. фактор $\mathrm {T} (V)$ по идеалу $I$ генерируется элементами формы $x\otimes x$. Конечно, для характеристики $0$ (или выше размерности векторного пространства) можно использовать то или иное определение произведения, поскольку обе алгебры изоморфны (см. В. И. Арнольд или Кобаяси-Номидзу).

Позволять $\mathrm {T} ^{r}(V)$ — пространство однородных тензоров степени $r$. Это натянуто на разложимые тензоры

$v_{1}\otimes \cdots \otimes v_{r},\quad v_{i}\in V.$

Антисимметризация ( или иногда косая симметризация ) разложимого тензора определяется выражением

$\operatorname {{\mathcal {A}}^{(r)}} (v_{1}\otimes \cdots \otimes v_{r})=\sum _{\sigma \in {\mathfrak {S}}_{r}}\operatorname {sgn} (\sigma )v_{\sigma (1)}\otimes \cdots \otimes v_{\sigma (r)}$

и когда $r!\neq 0$ (для ненулевого характеристического поля $r!$ может быть 0):

$\operatorname {Alt} ^{(r)}(v_{1}\otimes \cdots \otimes v_{r})={\frac {1}{r!}}\operatorname {{\mathcal {A}}^{(r)}} (v_{1}\otimes \cdots \otimes v_{r})$

где сумма берется по симметричной группе перестановок символов $\{1,\dots ,r\}$. Благодаря линейности и однородности это распространяется на операцию, также обозначаемую ${\mathcal {A}}$ и ${\rm {Alt}}$, на полной тензорной алгебре $\mathrm {T} (V)$.

Обратите внимание, что

$\operatorname {{\mathcal {A}}^{(r)}} \operatorname {{\mathcal {A}}^{(r)}} =r!\operatorname {{\mathcal {A}}^{(r)}} .$

Такого, что при определении $\operatorname {Alt} ^{(r)}$— проекция внешней (факторной) алгебры на r-однородное знакопеременное тензорное подпространство. С другой стороны, образ ${\mathcal {A}}(\mathrm {T} (V))$ всегда представляет собой знакопеременное тензорное градуированное подпространство (еще не алгебра, поскольку произведение еще не определено), обозначаемое $A(V)$. Это векторное подпространство $\mathrm {T} (V)$, и с этого момента оно наследует структуру градуированного векторного пространства $\mathrm {T} (V)$. Более того, ядро ${\mathcal {A}}^{(r)}$ это именно $I^{(r)}$, однородное подмножество идеала $I$, или ядро ${\mathcal {A}}$ является $I$. Когда $\operatorname {Alt}$ определено, $A(V)$ несет в себе ассоциативно-сортированный продукт ${\widehat {\otimes }}$ определяется (то же, что и произведение клина)

$t\wedge s=t~{\widehat {\otimes }}~s=\operatorname {Alt} (t\otimes s).$

Предполагая $K$ имеет характеристику 0, так как $A(V)$ является дополнением к $I$ в $\mathrm {T} (V)$, с указанным выше произведением существует канонический изоморфизм

$A(V)\cong {\textstyle \bigwedge }(V).$

Когда характеристика поля не равна нулю, ${\mathcal {A}}$ сделаю что ${\rm {Alt}}$делал раньше, но продукт не может быть определен, как указано выше. В таком случае изоморфизм $A(V)\cong {\textstyle \bigwedge }(V)$ по-прежнему сохраняется, несмотря на $A(V)$ не являющийся дополнением к идеалу $I$, но тогда продукт следует изменить, как указано ниже ( ${\dot {\wedge }}$ продукт, настройка Арнольда).

Наконец, мы всегда получаем $A(V)$ изоморфен с ${\textstyle \bigwedge }(V)$, но товар можно (или нужно) выбирать двумя способами (или только одним). На самом деле произведение можно было выбирать разными способами, масштабируя его на однородных пространствах как $c(r+p)/c(r)c(p)$ для произвольной последовательности $c(r)$ в поле, пока деление имеет смысл (при этом переопределенное произведение также является ассоциативным, т. е. определяет алгебру на $A(V)$). Также обратите внимание, что определение продукта интерьера должно быть соответствующим образом изменено, чтобы сохранить свойство асимметричного вывода.

Обозначение индекса

Предположим, что имеет конечную размерность n базис e ₁ , ... en _V V. , и что задан Тогда любой знакопеременный тензор t ∈ A ^р ( V ) ⊂ T ^р ( V ) можно записать в индексной записи с соблюдением соглашения Эйнштейна о суммировании как

$t=t^{i_{1}i_{2}\cdots i_{r}}\,{\mathbf {e} }_{i_{1}}\otimes {\mathbf {e} }_{i_{2}}\otimes \cdots \otimes {\mathbf {e} }_{i_{r}},$

где т ^{i ₁ ⋅⋅⋅ i _r} по полностью антисимметричен своим индексам.

Внешний продукт двух чередующихся тензоров t и s рангов r и p определяется выражением

$t~{\widehat {\otimes }}~s={\frac {1}{(r+p)!}}\sum _{\sigma \in {\mathfrak {S}}_{r+p}}\operatorname {sgn} (\sigma )t^{i_{\sigma (1)}\cdots i_{\sigma (r)}}s^{i_{\sigma (r+1)}\cdots i_{\sigma (r+p)}}{\mathbf {e} }_{i_{1}}\otimes {\mathbf {e} }_{i_{2}}\otimes \cdots \otimes {\mathbf {e} }_{i_{r+p}}.$

Компоненты этого тензора представляют собой в точности косую часть компонент тензорного произведения s ⊗ t , обозначаемую квадратными скобками над индексами:

$(t~{\widehat {\otimes }}~s)^{i_{1}\cdots i_{r+p}}=t^{[i_{1}\cdots i_{r}}s^{i_{r+1}\cdots i_{r+p}]}.$

Продукт для интерьера также можно описать в индексных обозначениях следующим образом. Позволять $t=t^{i_{0}i_{1}\cdots i_{r-1}}$ быть антисимметричным тензором ранга $r$. Тогда для α ∈ V ^∗ , $\iota _{\alpha }t$ является знакопеременным тензором ранга $r-1$, заданный

$(\iota _{\alpha }t)^{i_{1}\cdots i_{r-1}}=r\sum _{j=0}^{n}\alpha _{j}t^{ji_{1}\cdots i_{r-1}}.$

где n размерность V. —

Двойственность

Чередование операторов

Учитывая два векторных пространства V и X и натуральное число k , знакопеременный оператор из V ^к в X — полилинейное отображение

$f:V^{k}\to X$

такие, что если v ₁ , ..., v _k являются линейно зависимыми векторами из V , то

$f(v_{1},\ldots ,v_{k})=0.$

Карта

$w:V^{k}\to {\textstyle \bigwedge }^{\!k}(V),$

который ассоциируется с $k$ векторы из $V$ их внешний продукт, т. е. соответствующий им $k$-вектор, также является переменным. Фактически, это отображение является «наиболее общим» переменным оператором, определенным на $V^{k};$ учитывая любой другой альтернативный оператор $f:V^{k}\rightarrow X,$ существует единственное линейное отображение $\phi :{\textstyle \bigwedge }^{\!k}(V)\rightarrow X$ с $f=\phi \circ w.$ Это универсальное свойство характеризует пространство ${\textstyle \bigwedge }^{\!k}(V)$ и может служить ее определением.

Чередующиеся многолинейные формы

См. также: Переменная многолинейная карта.

Геометрическая интерпретация внешнего произведения ( n 1-форм ε , η , ω ) для получения n -формы («сетка» координатных поверхностей , здесь плоскостей), для n = 1, 2, 3 . «Тиражи» показывают ориентацию .

Вышеизложенное обсуждение специализируется на случае, когда $X=K$, базовое поле. В этом случае знакопеременная полилинейная функция

$f:V^{k}\to K$

называется знакопеременной полилинейной формой . Множество всех чередующихся полилинейных форм представляет собой векторное пространство, поскольку сумма двух таких отображений или произведение такого отображения на скаляр снова чередуется. По всеобщему свойству внешней силы пространство чередующихся форм степени $k$ на $V$ изоморфно естественно двойственному векторному пространству ${\bigl (}{\textstyle \bigwedge }^{\!k}(V){\bigr )}^{*}$. Если $V$ конечномерен, то последний естественно изоморфен к ${\textstyle \bigwedge }^{\!k}\left(V^{*}\right)$. В частности, если $V$ является $n$-мерность — размерность пространства чередующихся отображений из $V^{k}$ к $K$ биномиальный коэффициент $\textstyle {\binom {n}{k}}$.

При такой идентификации внешний продукт принимает конкретную форму: он производит новую антисимметричную карту из двух данных. Предположим, ω : V ^к → K и η : V ^м → K — две антисимметричные карты. Как и в случае с тензорными произведениями полилинейных отображений, число переменных их внешнего произведения есть сумма чисел их переменных. В зависимости от выбора идентификации элементов внешней власти с полилинейными формами внешнее произведение определяется как

$\omega \wedge \eta =\operatorname {Alt} (\omega \otimes \eta )$

или как

$\omega {\dot {\wedge }}\eta ={\frac {(k+m)!}{k!\,m!}}\operatorname {Alt} (\omega \otimes \eta ),$

где, если характеристика основного поля $K$ равно 0, чередование Alt полилинейной карты определяется как среднее значение скорректированных по знаку значений по всем перестановкам ее переменных:

$\operatorname {Alt} (\omega )(x_{1},\ldots ,x_{k})={\frac {1}{k!}}\sum _{\sigma \in S_{k}}\operatorname {sgn} (\sigma )\,\omega (x_{\sigma (1)},\ldots ,x_{\sigma (k)}).$

Когда поле $K$ имеет конечную характеристику , эквивалентная версия второго выражения без каких-либо факториалов или констант четко определена:

${\omega {\dot {\wedge }}\eta (x_{1},\ldots ,x_{k+m})}=\sum _{\sigma \in \mathrm {Sh} _{k,m}}\operatorname {sgn} (\sigma )\,\omega (x_{\sigma (1)},\ldots ,x_{\sigma (k)})\,\eta (x_{\sigma (k+1)},\ldots ,x_{\sigma (k+m)}),$

где здесь Sh _{k , m} ⊂ S _{k + m} — подмножество ( k , m ) тасовок : перестановок σ набора {1, 2, ..., k + m } таких, что σ (1) < σ (2 ) < ⋯ < σ ( k ) и σ ( k + 1) < σ ( k + 2) < ... < σ ( k + m ) . Поскольку это может выглядеть очень специфическим и точно настроенным, эквивалентной необработанной версией является суммирование в приведенной выше формуле по перестановкам в левых смежных классах S _{k + m} / ( S _k × S _m ) .

Интерьерное изделие

См. также: Интерьерные изделия.

Предположим, что $V$является конечномерным. Если $V^{*}$ обозначает пространство, двойственное к векторному пространству $V$, то для каждого $\alpha \in V^{*}$, можно определить первообразование на алгебре ${\textstyle \bigwedge }(V)$,

$\iota _{\alpha }:{\textstyle \bigwedge }^{\!k}(V)\rightarrow {\textstyle \bigwedge }^{\!k-1}(V).$

Этот вывод называется внутренним произведением с $\alpha$, или иногда оператор вставки , или сокращение на $\alpha$.

Предположим, что $w\in {\textstyle \bigwedge }^{\!k}(V)$. Затем $w$ представляет собой полилинейное отображение $V^{*}$ к $K$, поэтому он определяется своими значениями в k -кратном декартовом произведении $V^{*}\times V^{*}\times \dots \times V^{*}$. Если u ₁ , u ₂ , ..., u _{k −1} являются $k-1$ элементы $V^{*}$, затем определите

$(\iota _{\alpha }w)(u_{1},u_{2},\ldots ,u_{k-1})=w(\alpha ,u_{1},u_{2},\ldots ,u_{k-1}).$

Кроме того, пусть $\iota _{\alpha }f=0$ в любое время $f$ является чистым скаляром (т. е. принадлежит ${\textstyle \bigwedge }^{\!0}(V)$).

Аксиоматическая характеристика и свойства

Внутреннее изделие удовлетворяет следующим свойствам:

1. Для каждого $k$ и каждый $\alpha \in V^{*}$ (где по соглашению $\Lambda ^{-1}(V)=\{0\}$),

   $\iota _{\alpha }:{\textstyle \bigwedge }^{\!k}(V)\rightarrow {\textstyle \bigwedge }^{\!k-1}(V).$

2. Если $v$ является элементом $V$ ( $={\textstyle \bigwedge }^{\!1}(V)$), затем $\iota _{\alpha }v=\alpha (v)$ представляет собой двойственное спаривание между элементами $V$ и элементы $V^{*}$.
3. Для каждого $\alpha \in V^{*}$, $\iota _{\alpha }$ является градуированным выводом степени −1:

   $\iota _{\alpha }(a\wedge b)=(\iota _{\alpha }a)\wedge b+(-1)^{\deg a}a\wedge (\iota _{\alpha }b).$

Этих трех свойств достаточно, чтобы охарактеризовать интерьерное произведение, а также определить его в общем бесконечномерном случае.

К дополнительным свойствам внутреннего продукта относятся:

• $\iota _{\alpha }\circ \iota _{\alpha }=0.$
• $\iota _{\alpha }\circ \iota _{\beta }=-\iota _{\beta }\circ \iota _{\alpha }.$

Двойственность Ходжа

Основная статья: Звездный оператор Ходжа

Предположим, что $V$ имеет конечную размерность $n$. Тогда внутреннее произведение индуцирует канонический изоморфизм векторных пространств

${\textstyle \bigwedge }^{\!k}(V^{*})\otimes {\textstyle \bigwedge }^{\!n}(V)\to {\textstyle \bigwedge }^{\!n-k}(V)$

по рекурсивному определению

$\iota _{\alpha \wedge \beta }=\iota _{\beta }\circ \iota _{\alpha }.$

В геометрической настройке ненулевой элемент верхней внешней мощности ${\textstyle \bigwedge }^{\!n}(V)$(которое представляет собой одномерное векторное пространство) иногда называют формой объёма (или формой ориентации , хотя этот термин иногда может приводить к двусмысленности). Форма ориентации имени происходит от того факта, что выбор предпочтительного верхнего элемента определяет ориентацию всей внешней алгебры, поскольку это равносильно фиксации упорядоченного базиса векторного пространства. Относительно предпочтительной формы объема $\sigma$, изоморфизм задается явно выражением

${\textstyle \bigwedge }^{\!k}(V^{*})\to {\textstyle \bigwedge }^{\!n-k}(V):\alpha \mapsto \iota _{\alpha }\sigma .$

Если кроме объемной формы векторное пространство V снабжено скалярным произведением , идентифицирующим $V$ с $V^{*}$, то результирующий изоморфизм называется оператором звезды Ходжа , который отображает элемент в его двойственный элемент Ходжа :

$\star :{\textstyle \bigwedge }^{\!k}(V)\rightarrow {\textstyle \bigwedge }^{\!n-k}(V).$

Состав $\star$ с собой карты ${\textstyle \bigwedge }^{\!k}(V)\to {\textstyle \bigwedge }^{\!k}(V)$и всегда является скалярным кратным карты идентичности. В большинстве приложений форма объема совместима с внутренним произведением в том смысле, что она является внешним произведением базиса ортонормированного $V$. В этом случае,

$\star \circ \star :{\textstyle \bigwedge }^{\!k}(V)\to {\textstyle \bigwedge }^{\!k}(V)=(-1)^{k(n-k)+q}\mathrm {id}$

где id — тождественное отображение, а внутренний продукт имеет метрическую сигнатуру ( p , q ) — p плюсов и q минусов.

Внутренний продукт

Для $V$ конечномерное пространство, внутренний продукт (или псевдоевклидово внутренний продукт) на $V$ определяет изоморфизм $V$ с $V^{*}$, а значит, и изоморфизм ${\textstyle \bigwedge }^{\!k}(V)$ с ${\bigl (}{\textstyle \bigwedge }^{\!k}V{\bigr )}^{*}$. Соединение этих двух пространств также принимает форму внутреннего продукта. На разборном $k$-векторы,

$\left\langle v_{1}\wedge \cdots \wedge v_{k},w_{1}\wedge \cdots \wedge w_{k}\right\rangle =\det {\bigl (}\langle v_{i},w_{j}\rangle {\bigr )},$

определитель матрицы внутренних продуктов. В частном случае v _i = w _i скалярное произведение представляет собой квадратную норму k -вектора , заданную определителем матрицы Грама (⟨ v _i , v _j ⟩) . Затем это расширяется билинейно (или полуторалинейно в комплексном случае) до невырожденного внутреннего продукта на ${\textstyle \bigwedge }^{\!k}(V).$ Если e _i , i = 1, 2, ..., n , образуют ортонормированный базис $V$, то векторы вида

$e_{i_{1}}\wedge \cdots \wedge e_{i_{k}},\quad i_{1}<\cdots <i_{k},$

составляют ортонормированный базис для ${\textstyle \bigwedge }^{\!k}(V)$, утверждение, эквивалентное формуле Коши – Бине .

По отношению к внутреннему произведению внешнее умножение и внутреннее произведение взаимно сопряжены. В частности, для $\mathbf {v} \in {\textstyle \bigwedge }^{\!k-1}(V)$, $\mathbf {w} \in {\textstyle \bigwedge }^{\!k}(V)$, и $x\in V$,

$\langle x\wedge \mathbf {v} ,\mathbf {w} \rangle =\langle \mathbf {v} ,\iota _{x^{\flat }}\mathbf {w} \rangle$

где х ^♭ ∈ V ^∗ — музыкальный изоморфизм , линейный функционал, определяемый формулой

$x^{\flat }(y)=\langle x,y\rangle$

для всех $y\in V$. Это свойство полностью характеризует скалярное произведение на внешней алгебре.

Действительно, в более общем плане для $\mathbf {v} \in {\textstyle \bigwedge }^{\!k-l}(V)$, $\mathbf {w} \in {\textstyle \bigwedge }^{\!k}(V)$, и $\mathbf {x} \in {\textstyle \bigwedge }^{\!l}(V)$, итерация приведенных выше сопряженных свойств дает

$\langle \mathbf {x} \wedge \mathbf {v} ,\mathbf {w} \rangle =\langle \mathbf {v} ,\iota _{\mathbf {x} ^{\flat }}\mathbf {w} \rangle$

где сейчас $\mathbf {x} ^{\flat }\in {\textstyle \bigwedge }^{\!l}\left(V^{*}\right)\simeq {\bigl (}{\textstyle \bigwedge }^{\!l}(V){\bigr )}^{*}$ это двойной $l$-вектор, определяемый

$\mathbf {x} ^{\flat }(\mathbf {y} )=\langle \mathbf {x} ,\mathbf {y} \rangle$

для всех $\mathbf {y} \in {\textstyle \bigwedge }^{\!l}(V)$.

Структура биалгебры

Существует соответствие между градуированной двойственной градуированной алгеброй ${\textstyle \bigwedge }(V)$ и чередующиеся полилинейные формы на $V$. Внешняя алгебра (как и симметрическая алгебра ) наследует структуру биалгебры и, более того, структуру алгебры Хопфа от тензорной алгебры . См. статью о тензорных алгебрах для подробного рассмотрения этой темы.

Внешний продукт полилинейных форм, определенных выше, двойственен копроизведению, определенному на ${\textstyle \bigwedge }(V)$, дающий структуру коалгебры . Копроизведение является линейной функцией $\Delta :{\textstyle \bigwedge }(V)\to {\textstyle \bigwedge }(V)\otimes {\textstyle \bigwedge }(V)$, который определяется

$\Delta (v)=1\otimes v+v\otimes 1$

по элементам $v\in V$. Символ $1$ обозначает единичный элемент поля $K$. Напомним, что $K\simeq {\textstyle \bigwedge }^{\!0}(V)\subseteq {\textstyle \bigwedge }(V)$, так что вышесказанное действительно лежит в ${\textstyle \bigwedge }(V)\otimes {\textstyle \bigwedge }(V)$. Это определение копроизведения распространяется на все пространство. ${\textstyle \bigwedge }(V)$посредством (линейного) гомоморфизма. Правильная форма этого гомоморфизма — это не та форма, которую можно было бы наивно написать, а та, которая тщательно определена в статье о коалгебре . В этом случае получается

$\Delta (v\wedge w)=1\otimes (v\wedge w)+v\otimes w-w\otimes v+(v\wedge w)\otimes 1.$

Развернув это подробно, можно получить следующее выражение для разложимых элементов:

$\Delta (x_{1}\wedge \cdots \wedge x_{k})=\sum _{p=0}^{k}\;\sum _{\sigma \in Sh(p,k-p)}\;\operatorname {sgn} (\sigma )(x_{\sigma (1)}\wedge \cdots \wedge x_{\sigma (p)})\otimes (x_{\sigma (p+1)}\wedge \cdots \wedge x_{\sigma (k)}).$

где второе суммирование производится по всем ( p , k − p ) -перетасовкам . По соглашению считается, что Sh( k, 0) и Sh(0, k ) равны {id: {1, ..., k } → {1, ..., k }}. Также удобно брать чистые клиновые продукты. $v_{\sigma (1)}\wedge \dots \wedge v_{\sigma (p)}$ и $v_{\sigma (p+1)}\wedge \dots \wedge v_{\sigma (k)}$ равняться 1 для p = 0 и p = k соответственно (пустой продукт в ${\textstyle \bigwedge }(V)$). Перетасовка следует непосредственно из первой аксиомы коалгебры: относительного порядка элементов. $x_{k}$ сохраняется при перетасовке: перетасовка просто разбивает упорядоченную последовательность на две упорядоченные последовательности: одну слева и одну справа.

Заметим, что копроизведение сохраняет градуировку алгебры. Распространение на все пространство ${\textstyle {\textstyle \bigwedge }(V),}$ надо

$\Delta :{\textstyle \bigwedge }^{k}(V)\to \bigoplus _{p=0}^{k}{\textstyle \bigwedge }^{p}(V)\otimes {\textstyle \bigwedge }^{k-p}(V)$

Символ тензора ⊗, используемый в этом разделе, следует понимать с некоторой осторожностью: это не тот же самый символ тензора, который используется в определении знакопеременного произведения. Интуитивно, возможно, проще всего представить его как еще одно, но другое тензорное произведение: оно по-прежнему (билинейно) линейно, каким и должно быть тензорное произведение, но это произведение подходит для определения биалгебры, т. е. есть, для создания объекта ${\textstyle \bigwedge }(V)\otimes {\textstyle \bigwedge }(V)$. Любое затянувшееся сомнение можно развеять, поразмыслив над равенствами (1 ⊗ v ) ∧ (1 ⊗ w ) = 1 ⊗ ( v ∧ w ) и ( v ⊗ 1) ∧ (1 ⊗ w ) = v ⊗ w , которые следуют из определение коалгебры, в отличие от наивных манипуляций с символами тензора и клина. Более подробно это различие развито в статье о тензорных алгебрах . Здесь проблем гораздо меньше, поскольку чередующееся произведение $\wedge$ явно соответствует умножению во внешней алгебре, оставляя символ $\otimes$свободен для использования в определении биалгебры. На практике это не представляет особой проблемы, если только не попасть в фатальную ловушку замены чередующихся сумм $\otimes$символом клина, за одним исключением. Можно построить альтернативный продукт из $\otimes$, с пониманием, что это работает в другом пространстве. Сразу ниже дан пример: знакопеременное произведение для двойственного пространства может быть задано через копроизведение. Конструкция биалгебры здесь почти полностью аналогична конструкции в статье о тензорной алгебре , за исключением необходимости правильно отслеживать знаки чередования внешней алгебры.

С точки зрения копродукции внешний продукт в двойственном пространстве — это всего лишь градуированный двойник копродукции:

$(\alpha \wedge \beta )(x_{1}\wedge \cdots \wedge x_{k})=(\alpha \otimes \beta )\left(\Delta (x_{1}\wedge \cdots \wedge x_{k})\right)$

где тензорное произведение в правой части представляет собой полилинейные линейные отображения (расширенные нулем на элементы несовместимой однородной степени: точнее, α ∧ β = ε ∘ ( α ⊗ β ) ∘ Δ , где $\varepsilon$ — это единица, как она определена в настоящее время).

Единица — это гомоморфизм $\varepsilon :{\textstyle \bigwedge }(V)\to K$который возвращает компонент своего аргумента с нулевой оценкой. Копродукт и коединица вместе с внешним произведением определяют структуру биалгебры на внешней алгебре.

С антиподом , определенным на однородных элементах формулой $S(x)=(-1)^{\binom {{\text{deg}}\,x\,+1}{2}}x$внешняя алгебра, кроме того, является алгеброй Хопфа .

Функциональность

Предположим, что $V$ и $W$ представляют собой пару векторных пространств и $f:V\to W$представляет собой линейную карту . Тогда по свойству универсальности существует единственный гомоморфизм градуированных алгебр

${\textstyle \bigwedge }(f):{\textstyle \bigwedge }(V)\rightarrow {\textstyle \bigwedge }(W)$

такой, что

${\textstyle \bigwedge }(f)\left|_{{\textstyle \bigwedge }^{\!1}(V)}\right.=f:V={\textstyle \bigwedge }^{\!1}(V)\rightarrow W={\textstyle \bigwedge }^{\!1}(W).$

В частности, ${\textstyle \bigwedge }(f)$сохраняет однородную степень. k -градуированные компоненты ${\textstyle \bigwedge \left(f\right)}$ задаются на разложимых элементах выражением

${\textstyle \bigwedge }(f)(x_{1}\wedge \cdots \wedge x_{k})=f(x_{1})\wedge \cdots \wedge f(x_{k}).$

Позволять

${\textstyle \bigwedge }^{\!k}(f)={\textstyle \bigwedge }(f)\left|_{{\textstyle \bigwedge }^{\!k}(V)}\right.:{\textstyle \bigwedge }^{\!k}(V)\rightarrow {\textstyle \bigwedge }^{\!k}(W).$

Компоненты трансформации ${\textstyle \bigwedge }^{\!k}(f)$ относительно основы $V$ и $W$ это матрица $k\times k$ несовершеннолетние $f$. В частности, если $V=W$ и $V$ имеет конечную размерность $n$, затем ${\textstyle \bigwedge }^{\!n}(f)$ является отображением одномерного векторного пространства ${\textstyle \bigwedge }^{\!n}(V)$ , и поэтому задается скаляром: определителем самому себе $f$.

Точность

Если $0\to U\to V\to W\to 0$ — короткая точная последовательность векторных пространств, то

$0\to {\textstyle \bigwedge }^{\!1}(U)\wedge {\textstyle \bigwedge }(V)\to {\textstyle \bigwedge }(V)\to {\textstyle \bigwedge }(W)\to 0$

представляет собой точную последовательность градуированных векторных пространств, как есть

$0\to {\textstyle \bigwedge }(U)\to {\textstyle \bigwedge }(V).$

Прямые суммы

В частности, внешняя алгебра прямой суммы изоморфна тензорному произведению внешних алгебр:

${\textstyle \bigwedge }(V\oplus W)\cong {\textstyle \bigwedge }(V)\otimes {\textstyle \bigwedge }(W).$

Это градуированный изоморфизм; то есть,

${\textstyle \bigwedge }^{\!k}(V\oplus W)\cong \bigoplus _{p+q=k}{\textstyle \bigwedge }^{\!p}(V)\otimes {\textstyle \bigwedge }^{\!q}(W).$

В большей общности для короткой точной последовательности векторных пространств ${\textstyle 0\to U\mathrel {\overset {f}{\to }} V\mathrel {\overset {g}{\to }} W\to 0,}$ есть естественная фильтрация

$0=F^{0}\subseteq F^{1}\subseteq \cdots \subseteq F^{k}\subseteq F^{k+1}={\textstyle \bigwedge }^{\!k}(V)$

где $F^{p}$ для $p\geq 1$ состоит из элементов формы $u_{1}\wedge \ldots \wedge u_{k+1-p}\wedge v_{1}\wedge \ldots v_{p-1}$ для $u_{i}\in U$ и $v_{i}\in V.$ Соответствующие факторы допускают естественный изоморфизм

$F^{p+1}/F^{p}\cong {\textstyle \bigwedge }^{\!k-p}(U)\otimes {\textstyle \bigwedge }^{\!p}(W)$ данный $u_{1}\wedge \ldots \wedge u_{k-p}\wedge v_{1}\wedge \ldots \wedge v_{p}\mapsto u_{1}\wedge \ldots \wedge u_{k-p}\otimes g(v_{1})\wedge \ldots \wedge g(v_{p}).$

В частности, если U одномерен, то

$0\to U\otimes {\textstyle \bigwedge }^{\!k-1}(W)\to {\textstyle \bigwedge }^{\!k}(V)\to {\textstyle \bigwedge }^{\!k}(W)\to 0$

точно, и если W одномерно, то

$0\to {\textstyle \bigwedge }^{k}(U)\to {\textstyle \bigwedge }^{\!k}(V)\to {\textstyle \bigwedge }^{\!k-1}(U)\otimes W\to 0$

это точно.

Приложения

Ориентированный объем в аффинном пространстве

Естественная обстановка для (ориентированного) $k$-мерный объем и внешняя алгебра - аффинное пространство . Это также тесная связь между внешней алгеброй и дифференциальными формами , поскольку для интегрирования нам нужен «дифференциальный» объект для измерения бесконечно малого объема. Если $\mathbb {A}$ является аффинным пространством над векторным пространством $V$и ( симплексный ) набор упорядоченных $k+1$ точки $A_{0},A_{1},...,A_{k}$, мы можем определить его ориентированную $k$-мерный объем как внешнее произведение векторов $A_{0}A_{1}\wedge A_{0}A_{2}\wedge \cdots \wedge A_{0}A_{k}={}$ $(-1)^{j}A_{j}A_{0}\wedge A_{j}A_{1}\wedge A_{j}A_{2}\wedge \cdots \wedge A_{j}A_{k}$ (с использованием конкатенации $PQ$ иметь в виду вектор смещения из точки $P$ к $Q$); если изменить порядок точек, то ориентированный объем изменится на знак в соответствии с четностью перестановки. В $n$-мерное пространство, объём любого $n$-мерный симплекс скалярно кратен любому другому.

Сумма $(k-1)$-мерные ориентированные области граничных симплексов $k$-мерный симплекс равен нулю, как и сумма векторов вокруг треугольника или ориентированных треугольников, ограничивающих тетраэдр в предыдущем разделе.

Структура векторного пространства на ${\textstyle \bigwedge }(V)$ обобщает сложение векторов в $V$: у нас есть $(u_{1}+u_{2})\wedge v=u_{1}\wedge v+u_{2}\wedge v$ и аналогично k -лезвие $v_{1}\wedge \dots \wedge v_{k}$ линейна по каждому фактору.

Линейная алгебра

В приложениях к алгебре внешний продукт обеспечивает абстрактный алгебраический способ описания определителя и миноров матрицы линейной . Например, хорошо известно, что определитель квадратной матрицы равен объему параллелоэдра, стороны которого являются столбцами матрицы (со знаком, указывающим ориентацию). Это предполагает, что определитель может быть определен через внешнее произведение векторов-столбцов. Аналогично, k × k миноры матрицы можно определить, рассматривая внешние произведения векторов-столбцов, выбранных k за раз. Эти идеи можно распространить не только на матрицы, но и на линейные преобразования : определителем линейного преобразования является фактор, с помощью которого оно масштабирует ориентированный объем любого заданного эталонного параллелоэдра. Таким образом, определитель линейного преобразования можно определить с точки зрения того, что преобразование делает с высшей внешней степенью. Действие трансформации на меньшие внешние силы дает базис -независимый способ говорить о минорах трансформации.

Физика

Основная статья: Электромагнитный тензор

В физике многие величины естественным образом представляются знакопеременными операторами. Например, если движение заряженной частицы описывается векторами скорости и ускорения в четырехмерном пространстве-времени, то для нормализации вектора скорости требуется, чтобы электромагнитная сила была знакопеременным оператором скорости. Его шесть степеней свободы отождествляются с электрическим и магнитным полями.

Электромагнитное поле

В теориях относительности Эйнштейна электромагнитное поле обычно представляется как дифференциальная 2-форма. $F=dA$ в 4-мерном пространстве или как эквивалентное переменное тензорное поле $F_{ij}=A_{[i,j]}=A_{[i;j]},$электромагнитный тензор . Затем $dF=ddA=0$ или эквивалентное тождество Бьянки $F_{[ij,k]}=F_{[ij;k]}=0.$ Ничто из этого не требует метрики.

Добавление метрики Лоренца и ориентации дает оператор звезды Ходжа. $\star$ и, таким образом, позволяет определить $J={\star }d{\star }F$ или эквивалентная тензорная дивергенция $J^{i}=F_{,j}^{ij}=F_{;j}^{ij}$ где $F^{ij}=g^{ik}g^{jl}F_{kl}.$

Линейная геометрия

Разложимые k -векторы имеют геометрическую интерпретацию: бивектор $u\wedge v$ представляет собой плоскость, натянутую векторами, «взвешенными» числом, определяемым площадью ориентированного параллелограмма со сторонами $u$ и $v$. Аналогично, 3-вектор $u\wedge v\wedge w$ представляет собой натянутое трехмерное пространство, взвешенное по объему ориентированного параллелепипеда с ребрами $u$, $v$, и $w$.

Проективная геометрия

Разложимые k -векторы в ${\textstyle \bigwedge }^{\!k}(V)$ соответствуют взвешенным k -мерным линейным подпространствам $V$. В частности, грассманиан -мерных k подпространств $V$, обозначенный $\operatorname {Gr} _{k}(V)$, естественно отождествляется с алгебраическим подмногообразием проективного пространства ${\textstyle \mathbf {P} {\bigl (}{\textstyle \bigwedge }^{\!k}(V){\bigr )}}$. Это называется вложением Плюккера , и образ вложения можно охарактеризовать отношениями Плюккера .

Дифференциальная геометрия

Внешняя алгебра имеет заметные применения в дифференциальной геометрии , где она используется для определения дифференциальных форм . Дифференциальные формы — это математические объекты, которые оценивают длину векторов, площади параллелограммов и объемы тел более высокой размерности , поэтому их можно интегрировать по кривым, поверхностям и многообразиям более высокой размерности таким образом, чтобы обобщать линейные и поверхностные интегралы из исчисления. . Дифференциальная форма в точке дифференцируемого многообразия — это знакопеременная полилинейная форма на касательном пространстве в этой точке. Эквивалентно, дифференциальная форма степени k представляет собой линейный функционал от k -й внешней степени касательного пространства. Как следствие, внешний продукт полилинейных форм определяет естественный внешний продукт дифференциальных форм. Дифференциальные формы играют важную роль в различных областях дифференциальной геометрии.

Альтернативный подход определяет дифференциальные формы в терминах ростков функций .

В частности, внешняя производная придает внешней алгебре дифференциальных форм на многообразии структуру дифференциально-градуированной алгебры . Внешняя производная коммутирует с обратным образом вдоль гладких отображений между многообразиями и, следовательно, является естественным дифференциальным оператором . Внешняя алгебра дифференциальных форм, снабженная внешней производной, представляет собой коцепный комплекс , когомологии которого называются когомологиями де Рама основного многообразия и играют жизненно важную роль в алгебраической топологии дифференцируемых многообразий.

Теория представлений

В теории представлений внешняя алгебра является одним из двух фундаментальных функторов Шура в категории векторных пространств, а другой является симметричной алгеброй . Вместе эти конструкции используются для генерации неприводимых представлений полной линейной группы (см. Фундаментальное представление ).

Суперпространство

Внешняя алгебра над комплексными числами является архетипическим примером супералгебры , которая играет фундаментальную роль в физических теориях, касающихся фермионов и суперсимметрии . Отдельный элемент внешней алгебры называется сверхчислом . или число Грассмана . Сама внешняя алгебра тогда является просто одномерным суперпространством : это просто набор всех точек внешней алгебры. Топология этого пространства по существу является слабой топологией , открытые множества представляют собой цилиндрические множества . n - мерное суперпространство — это всего лишь $n$-кратное произведение внешних алгебр.

алгебры

Позволять $L$ быть алгеброй Ли над полем $K$, то можно определить структуру цепного комплекса на внешней алгебре $L$. Это $K$-линейное картографирование

$\partial :{\textstyle \bigwedge }^{\!p+1}(L)\to {\textstyle \bigwedge }^{\!p}(L)$

определяется на разложимых элементах формулой

$\partial (x_{1}\wedge \cdots \wedge x_{p+1})={\frac {1}{p+1}}\sum _{j<\ell }(-1)^{j+\ell +1}[x_{j},x_{\ell }]\wedge x_{1}\wedge \cdots \wedge {\hat {x}}_{j}\wedge \cdots \wedge {\hat {x}}_{\ell }\wedge \cdots \wedge x_{p+1}.$

Тождество Якоби справедливо тогда и только тогда, когда ${1}$, и, следовательно, это необходимое и достаточное условие антикоммутативной неассоциативной алгебры $L$быть алгеброй Ли. Более того, в таком случае ${\textstyle {\textstyle \bigwedge }(L)}$ представляет собой цепной комплекс с граничным оператором $\partial$. Гомологии , связанные с этим комплексом, являются гомологиями алгебры Ли .

Гомологическая алгебра

Внешняя алгебра является основным компонентом построения комплекса Кошуля — фундаментального объекта гомологической алгебры .

История

Внешняя алгебра была впервые введена Германом Грассманом в 1844 году под общим термином Ausdehnungslehre , или Теория Расширения . В более общем смысле это относилось к алгебраической (или аксиоматической) теории расширенных величин и было одним из ранних предшественников современного понятия векторного пространства . Сен-Венан также опубликовал аналогичные идеи внешнего исчисления, в которых он заявлял о приоритете над Грассманом.

Сама алгебра была построена на основе набора правил или аксиом, отражающих формальные аспекты теории мультивекторов Кэли и Сильвестра. Таким образом, это было исчисление , во многом похожее на исчисление высказываний , за исключением того, что оно было сосредоточено исключительно на задаче формального рассуждения в геометрических терминах. В частности, эта новая разработка позволила аксиоматически охарактеризовать размерность — свойство, которое ранее рассматривалось только с координатной точки зрения.

Значение этой новой теории векторов и мультивекторов было потеряно для математиков середины XIX века. до тех пор, пока не была тщательно проверена Джузеппе Пеано в 1888 году. Работа Пеано также оставалась несколько неясной до начала века, когда предмет был объединен членами французской геометрической школы (особенно Анри Пуанкаре , Эли Картаном и Гастоном Дарбу ), которые применяли теорию Грассмана. идеи к исчислению дифференциальных форм .

Некоторое время спустя Альфред Норт Уайтхед , заимствуя идеи Пеано и Грассмана, представил свою универсальную алгебру . Это затем проложило путь развитию абстрактной алгебры в 20-м веке , поставив аксиоматическое понятие алгебраической системы на прочную логическую основу.

См. также

• Альтернативная алгебра
• Внешнее исчисление идентичности
• Алгебра Клиффорда , обобщение внешней алгебры до ненулевой квадратичной формы.
• Геометрическая алгебра
• Рубашка комплексная
• Полилинейная алгебра
• Симметричная алгебра , симметричный аналог
• Тензорная алгебра
• Алгебра Вейля , квантовая деформация симметрической алгебры симплектической формой.

Ссылки

Математические ссылки

• Бишоп, Р .; Гольдберг, С.И. (1980), Тензорный анализ многообразий , Дувр, ISBN  0-486-64039-6

  Включает рассмотрение чередующихся тензоров и чередующихся форм, а также подробное обсуждение двойственности Ходжа с точки зрения, принятой в этой статье.

• Бурбаки, Николя (1989), Элементы математики, Алгебра I , Springer-Verlag, ISBN  3-540-64243-9

  Это основной математический справочник статьи. Он знакомит с внешней алгеброй модуля над коммутативным кольцом (хотя эта статья специализируется в первую очередь на случае, когда кольцо является полем), включая обсуждение свойств универсальности, функториальности, двойственности и структуры биалгебры. См. §III.7 и §III.11.

• Брайант, РЛ ; Чернь, СС ; Гарднер, РБ; Гольдшмидт, Х.Л.; Гриффитс, Пенсильвания (1991), Внешние дифференциальные системы , Springer-Verlag

  Эта книга содержит приложения внешних алгебр к задачам уравнений в частных производных . Ранг и связанные с ним концепции разрабатываются в первых главах.

• Мак Лейн, С .; Биркгоф, Г. (1999), Алгебра , AMS Челси, ISBN  0-8218-1646-2

  Разделы 6–10 главы XVI дают более элементарное описание внешней алгебры, включая двойственность, определители и миноры, а также альтернативные формы.

• Штернберг, Шломо (1964), Лекции по дифференциальной геометрии , Прентис Холл

  Содержит классическую трактовку внешней алгебры как знакопеременных тензоров и приложения к дифференциальной геометрии.

Исторические справки

• Бурбаки (1989 , Историческая справка по главам II и III)
• Клиффорд, В. (1878), «Приложения обширной алгебры Грассмана», Американский журнал математики , 1 (4), The Johns Hopkins University Press: 350–358, doi : 10.2307/2369379 , JSTOR   2369379
• Фордер, Х.Г. (1941), Исчисление расширения , Интернет-архив
• Грассманн, Герман (1844), «Теория линейного расширения (на немецком языке) - новая ветвь математики» Альтернативный справочник
• Канненберг, Ллойд (2000), Грассмана Теория расширения (перевод Ausdehnungslehre ) , Американское математическое общество, ISBN  0-8218-2031-1
• Пеано, Джузеппе (1888), « Геометрическое исчисление в соответствии с Ausdehnungslehre Х. Грассмана, которому предшествуют операции дедуктивной логики» ; Канненберг, Ллойд (1999), Геометрическое исчисление: согласно Ausdehnungslehre Х. Грассмана , Биркхойзер, ISBN  978-0-8176-4126-9 .
• Уайтхед, Альфред Норт (1898), «Трактат об универсальной алгебре с приложениями» , Nature , 58 (1504), Кембридж: 385, Бибкод : 1898Natur..58..385G , doi : 10.1038/058385a0 , S2CID   3985954

Другие ссылки и дополнительная литература

• Браун, Дж. М. (2007), Алгебра Грассмана - Исследование приложений расширенной векторной алгебры с помощью Mathematica , заархивировано из оригинала 19 февраля 2009 г. , получено 9 мая 2007 г.

  Введение во внешнюю алгебру и геометрическую алгебру с акцентом на приложения. Также включает раздел истории и библиографию.

• Спивак, Майкл (1965), Исчисление на многообразиях , Аддисон-Уэсли, ISBN  978-0-8053-9021-6

  Включает приложения внешней алгебры к дифференциальным формам, уделяя особое внимание интегрированию и теореме Стокса . Обозначения ${\textstyle {\textstyle \bigwedge }^{\!k}V}$в этом тексте используется для обозначения пространства знакопеременных k -форм на V ; то есть для Спивака ${\textstyle {\textstyle \bigwedge }^{\!k}V}$ так будет называться эта статья ${\textstyle {\textstyle \bigwedge }^{\!k}V^{*}.}$ Спивак обсуждает это в Приложении 4.

• Стрэнг, Г. (1993), Введение в линейную алгебру , Wellesley-Cambridge Press, ISBN  978-0-9614088-5-5

  Включает элементарную обработку аксиоматизации определителей как знаковых площадей, объемов и объемов более высокой размерности.

• Онищик А.Л. (2001) [1994], «Внешняя алгебра» , Энциклопедия математики , EMS Press
• Венделл, Флеминг (2012) [1977], «7. Внешняя алгебра и дифференциальное исчисление» , Функции нескольких переменных (2-е изд.), Springer, стр. 275–320, ISBN  978-1-4684-9461-7

  Этот учебник по многомерному исчислению ловко вводит внешнюю алгебру дифференциальных форм в последовательность вычислений для колледжей.

• Шафаревич, ИР ; Ремизов, АО (2012). Линейная алгебра и геометрия . Спрингер . ISBN  978-3-642-30993-9 .

  Глава 10: Внешнее произведение и внешние алгебры

• «Метод Грассмана в проективной геометрии». Сборник английских переводов трех заметок Чезаре Бурали-Форти о применении внешней алгебры к проективной геометрии.
• К. Бурали-Форти, «Введение в дифференциальную геометрию по методу Х. Грассмана». Английский перевод ранней книги по геометрическим приложениям внешних алгебр.
• «Механика в соответствии с принципами теории расширения». Английский перевод статей одного Грассмана о приложениях внешней алгебры.