Определитель

Эта статья о математике. Информацию о детерминантах эпидемиологии см. в разделе «Фактор риска» . Информацию о детерминантах в иммунологии см. в разделе «Эпитоп» .

В математике определитель , — это скалярная величина являющаяся определенной функцией элементов квадратной матрицы . Определитель матрицы A обычно обозначается det( A ) , det A или | А | . Его значение характеризует некоторые свойства матрицы и линейного отображения , представляемого по заданному базису матрицей. В частности, определитель отличен от нуля тогда и только тогда, когда матрица обратима и соответствующее линейное отображение является изоморфизмом . Определителем произведения матриц является произведение их определителей.

Определитель матрицы 2 × 2 равен

${\begin{vmatrix}a&b\\c&d\end{vmatrix}}=ad-bc,$

а определитель матрицы 3 × 3 равен

${\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}=aei+bfg+cdh-ceg-bdi-afh.$

Определитель матрицы размера n × n можно определить несколькими эквивалентными способами, наиболее распространенным из которых является формула Лейбница , которая выражает определитель как сумму $n!$( факториал n ) знаковые произведения элементов матрицы. Его можно вычислить с помощью расширения Лапласа , которое выражает определитель как линейную комбинацию определителей подматриц, или с помощью метода исключения Гаусса , который выражает определитель как произведение диагональных элементов диагональной матрицы , полученной последовательностью элементарных вычислений . операции со строками .

Определители также могут определяться некоторыми из их свойств. А именно, определитель — это уникальная функция, определенная на матрицах размера n × n , которая обладает четырьмя следующими свойствами:

1. Определитель единичной матрицы равен 1 .
2. Обмен двух строк умножает определитель на −1 .
3. Умножение строки на число умножает определитель на это число.
4. Добавление к строке числа, кратного другой строке, не меняет определитель.

Вышеуказанные свойства, относящиеся к строкам (свойства 2–4), могут быть заменены соответствующими утверждениями, относящимися к столбцам.

Определитель квадратной матрицы также может быть определен непосредственно через соответствующий линейный эндоморфизм, представленный матрицей. Поскольку определитель инвариантен относительно преобразования подобия матриц, он на самом деле зависит только от линейного преобразования и в принципе может быть определен полностью «бескоординатным» способом, то есть без использования какого-либо выбора матричного представления.

Определители встречаются во всей математике. Например, для представления коэффициентов в системе линейных уравнений часто используется матрица , а для решения этих уравнений можно использовать определители ( правило Крамера ), хотя другие методы решения в вычислительном отношении гораздо более эффективны. Определители используются для определения характеристического многочлена квадратной матрицы, корнями которого являются собственные значения . В геометрии знаковый n -мерный объем n - мерного параллелепипеда выражается определителем, а определитель линейного эндоморфизма определяет, как ориентация и n преобразуются -мерный объем под действием эндоморфизма. Это используется в исчислении с внешними дифференциальными формами и определителем Якобиана , в частности, для замены переменных в кратных интегралах .

Матрицы два на два

Определитель 2 × 2 матрицы ${\begin{pmatrix}a&b\\c&d\end{pmatrix}}$ обозначается либо « det », либо вертикальными чертами вокруг матрицы и определяется как

$\det {\begin{pmatrix}a&b\\c&d\end{pmatrix}}={\begin{vmatrix}a&b\\c&d\end{vmatrix}}=ad-bc.$

Например,

$\det {\begin{pmatrix}3&7\\1&-4\end{pmatrix}}={\begin{vmatrix}3&7\\1&{-4}\end{vmatrix}}=(3\cdot (-4))-(7\cdot 1)=-19.$

Первые свойства

Определитель имеет несколько ключевых свойств, которые можно доказать путем непосредственной оценки определения для $2\times 2$-матрицы, и это продолжает сохраняться для определителей более крупных матриц. Они заключаются в следующем: во-первых, определитель единичной матрицы ${\begin{pmatrix}1&0\\0&1\end{pmatrix}}$это 1. Во-вторых, определитель равен нулю, если две строки одинаковы:

${\begin{vmatrix}a&b\\a&b\end{vmatrix}}=ab-ba=0.$

Это справедливо и в том случае, если два столбца одинаковы. Более того,

${\begin{vmatrix}a&b+b'\\c&d+d'\end{vmatrix}}=a(d+d')-(b+b')c={\begin{vmatrix}a&b\\c&d\end{vmatrix}}+{\begin{vmatrix}a&b'\\c&d'\end{vmatrix}}.$

Наконец, если какой-либо столбец умножить на некоторое число $r$ (т. е. все записи в этом столбце умножаются на это число), определитель также умножается на это число:

${\begin{vmatrix}r\cdot a&b\\r\cdot c&d\end{vmatrix}}=rad-brc=r(ad-bc)=r\cdot {\begin{vmatrix}a&b\\c&d\end{vmatrix}}.$

Геометрический смысл

Площадь параллелограмма — это абсолютное значение определителя матрицы, образованной векторами, представляющими стороны параллелограмма.

Если элементы матрицы являются действительными числами, матрица A может использоваться для представления двух линейных карт : одна, которая отображает стандартные базисные векторы в строки A которая отображает их в столбцы A. , и другая , В любом случае изображения базисных векторов образуют параллелограмм , который представляет собой изображение единичного квадрата при отображении. Параллелограмм, определенный строками приведенной выше матрицы, имеет вершины в (0, 0) , ( a , b ) , ( a + c , b + d ) и ( c , d ) , как показано в сопроводительном документе. диаграмма.

Абсолютное значение ad − bc — это площадь параллелограмма и, таким образом, представляет собой масштабный коэффициент, с помощью которого площади преобразуются с A. помощью (Параллелограмм, образованный столбцами A , вообще говоря, является другим параллелограммом, но поскольку определитель симметричен относительно строк и столбцов, площадь будет той же.)

Абсолютное значение определителя вместе со знаком становится ориентированной площадью параллелограмма. Ориентированная область такая же, как и обычная площадь , за исключением того, что она отрицательна, когда угол между первым и вторым вектором, определяющим параллелограмм, поворачивается по часовой стрелке (что противоположно направлению, которое можно было бы получить для единичной матрицы ).

Чтобы показать, что ad − bc является областью со знаком, можно рассмотреть матрицу, содержащую два вектора u ≡ ( a , b ) и v ≡ ( c , d ) , представляющие стороны параллелограмма. Подписанную область можно выразить как | ты | | в | sin θ для угла θ между векторами, который равен просто основанию, умноженному на высоту, длину одного вектора, умноженную на перпендикулярную составляющую другого. Из-за синуса это уже площадь со знаком, но ее можно выразить более удобно, используя косинус дополнительного угла к перпендикулярному вектору, например u ^⊥ знак равно (− b , a ) , так что | ты ^⊥ | | в | cos θ ' становится рассматриваемой областью со знаком, которую можно определить по образцу скалярного произведения , равного ad - bc , согласно следующим уравнениям:

${\text{Signed area}}=|{\boldsymbol {u}}|\,|{\boldsymbol {v}}|\,\sin \,\theta =\left|{\boldsymbol {u}}^{\perp }\right|\,\left|{\boldsymbol {v}}\right|\,\cos \,\theta '={\begin{pmatrix}-b\\a\end{pmatrix}}\cdot {\begin{pmatrix}c\\d\end{pmatrix}}=ad-bc.$

Объем этого параллелепипеда есть абсолютное значение определителя матрицы, образованной столбцами, построенными из векторов r1, r2 и r3.

Таким образом, определитель дает масштабный коэффициент и ориентацию, индуцированную отображением, представленным A . Когда определитель равен единице, линейное отображение, определяемое матрицей, является равноплощадным и сохраняющим ориентацию.

объект, известный как бивектор С этими идеями связан . В 2D его можно интерпретировать как ориентированный плоский сегмент , образованный путем представления двух векторов, каждый из которых имеет начало координат (0, 0) и координаты ( a , b ) и ( c , d ) . Величина бивектора (обозначается ( a , b ) ∧ ( c , d ) ) — это площадь со знаком , которая также является определителем ad − bc .

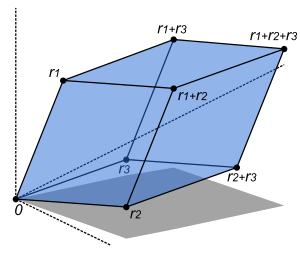
Если размера n × n действительная матрица A записана через ее векторы-столбцы $A=\left[{\begin{array}{c|c|c|c}\mathbf {a} _{1}&\mathbf {a} _{2}&\cdots &\mathbf {a} _{n}\end{array}}\right]$, затем

$A{\begin{pmatrix}1\\0\\\vdots \\0\end{pmatrix}}=\mathbf {a} _{1},\quad A{\begin{pmatrix}0\\1\\\vdots \\0\end{pmatrix}}=\mathbf {a} _{2},\quad \ldots ,\quad A{\begin{pmatrix}0\\0\\\vdots \\1\end{pmatrix}}=\mathbf {a} _{n}.$

Это значит, что $A$ отображает единичный n -куб в n -мерный параллелоэдр , определяемый векторами $\mathbf {a} _{1},\mathbf {a} _{2},\ldots ,\mathbf {a} _{n},$ область $P=\left\{c_{1}\mathbf {a} _{1}+\cdots +c_{n}\mathbf {a} _{n}\mid 0\leq c_{i}\leq 1\ \forall i\right\}.$

Определитель дает знаковый n -мерный объем этого параллелоэдра: $\det(A)=\pm {\text{vol}}(P),$ и, следовательно, в более общем смысле описывает n -мерный масштабный коэффициент объема линейного преобразования , производимого A . (Знак показывает, сохраняет ли преобразование ориентацию или меняет ее .) В частности, если определитель равен нулю, то этот параллелоэдр имеет нулевой объем и не является полностью n -мерным, что указывает на то, что размерность образа A меньше n . Это означает , что A производит линейное преобразование, которое не является ни однозначным , ни однозначным , и поэтому не является обратимым.

Определение

Пусть A — квадратная матрица с n строками и n столбцами, так что ее можно записать как

$A={\begin{bmatrix}a_{1,1}&a_{1,2}&\cdots &a_{1,n}\\a_{2,1}&a_{2,2}&\cdots &a_{2,n}\\\vdots &\vdots &\ddots &\vdots \\a_{n,1}&a_{n,2}&\cdots &a_{n,n}\end{bmatrix}}.$

Записи $a_{1,1}$и т. д. во многих случаях являются действительными или комплексными числами. Как обсуждается ниже, определитель также определен для матриц, элементы которых находятся в коммутативном кольце .

Определитель A обозначается det( A ), или его можно обозначить непосредственно через элементы матрицы, написав заключающие столбцы вместо скобок:

${\begin{vmatrix}a_{1,1}&a_{1,2}&\cdots &a_{1,n}\\a_{2,1}&a_{2,2}&\cdots &a_{2,n}\\\vdots &\vdots &\ddots &\vdots \\a_{n,1}&a_{n,2}&\cdots &a_{n,n}\end{vmatrix}}.$

Существуют различные эквивалентные способы определения определителя квадратной матрицы A , то есть матрицы с одинаковым количеством строк и столбцов: определитель может быть определен с помощью формулы Лейбница , явной формулы, включающей суммы произведений определенных элементов матрицы. Определитель также можно охарактеризовать как уникальную функцию, зависящую от элементов матрицы, удовлетворяющих определенным свойствам. Этот подход также можно использовать для вычисления определителей путем упрощения рассматриваемых матриц.

Формула Лейбница

Основная статья: формула Лейбница для определителей

Матрицы 3 × 3

Формула Лейбница для определителя матрицы 3 × 3 имеет следующий вид:

${\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}=aei+bfg+cdh-ceg-bdi-afh.\$

В этом выражении каждый термин имеет один множитель из каждой строки, все в разных столбцах, расположенных в порядке возрастания строк. Например, bdi имеет b из второго столбца первой строки, d из первого столбца второй строки и i из третьего столбца третьей строки. Знаки определяются тем, сколько транспозиций факторов необходимо, чтобы расположить факторы в порядке возрастания их столбцов (при условии, что члены располагаются слева направо в порядке возрастания порядка строк): положительный при четном числе транспозиций и отрицательный при нечетное число. В примере с bdi однократное транспонирование bd в db дает dbi, три множителя которого взяты из первого, второго и третьего столбцов соответственно; это нечетное количество транспозиций, поэтому термин имеет отрицательный знак.

Правило Сарруса

Правило Сарруса представляет собой мнемонику расширенной формы этого определителя: сумма произведений трех диагональных линий матричных элементов с северо-запада на юго-восток минус сумма произведений трех диагональных линий с юго-запада на северо-восток. восточные строки элементов, когда рядом с ней пишутся копии первых двух столбцов матрицы, как на иллюстрации. Эта схема вычисления определителя матрицы 3×3 не переносится на более высокие измерения.

n × n матрицы

Обобщая вышеизложенное на более высокие измерения, определитель $n\times n$Матрица — это выражение, включающее перестановки и их подписи . Перестановка набора $\{1,2,\dots ,n\}$ является биективной функцией $\sigma$ из этого набора в себя, со значениями $\sigma (1),\sigma (2),\ldots ,\sigma (n)$исчерпать весь набор. Множество всех таких перестановок, называемое симметричной группой , обычно обозначается $S_{n}$. Подпись $\operatorname {sgn}(\sigma )$ перестановки $\sigma$ является $+1,$если перестановку можно получить четным числом транспозиций (обменами двух записей); в противном случае это $-1.$

Дана матрица

$A={\begin{bmatrix}a_{1,1}\ldots a_{1,n}\\\vdots \qquad \vdots \\a_{n,1}\ldots a_{n,n}\end{bmatrix}},$

формула Лейбница для его определителя, используя сигма-обозначение суммы, равна

$\det(A)={\begin{vmatrix}a_{1,1}\ldots a_{1,n}\\\vdots \qquad \vdots \\a_{n,1}\ldots a_{n,n}\end{vmatrix}}=\sum _{\sigma \in S_{n}}\operatorname {sgn}(\sigma )a_{1,\sigma (1)}\cdots a_{n,\sigma (n)}.$

Используя обозначение числа Пи для продукта, его можно сократить до

$\det(A)=\sum _{\sigma \in S_{n}}\left(\operatorname {sgn}(\sigma )\prod _{i=1}^{n}a_{i,\sigma (i)}\right)$.

Символ Леви -Чивита $\varepsilon _{i_{1},\ldots ,i_{n}}$ определяется на n - кортежах целых чисел в $\{1,\ldots ,n\}$как 0 , если два целых числа равны, и в противном случае как сигнатура перестановки, определенной кортежем из n целых чисел. С символом Леви-Чивита формула Лейбница принимает вид

$\det(A)=\sum _{i_{1},i_{2},\ldots ,i_{n}}\varepsilon _{i_{1}\cdots i_{n}}a_{1,i_{1}}\!\cdots a_{n,i_{n}},$

где сумма берется по всем n -кортежам целых чисел в $\{1,\ldots ,n\}.$

Свойства определителя

Характеристика определителя

Определитель можно охарактеризовать следующими тремя ключевыми свойствами. Чтобы сформулировать это, удобно рассмотреть $n\times n$-матрица А как составленная из ее $n$ столбцы, так называемые

$A={\big (}a_{1},\dots ,a_{n}{\big )},$

где вектор-столбец $a_{i}$ (для каждого i ) состоит из элементов матрицы i -го столбца.

2. $\det \left(I\right)=1$, где $I$ является единичной матрицей .
4. Определитель полилинейный : если j -й столбец матрицы $A$ записывается как линейная комбинация $a_{j}=r\cdot v+w$ двух вектор-столбцов v и w и числа r , то определитель A выражается в виде аналогичной линейной комбинации:

   ${\begin{aligned}|A|&={\big |}a_{1},\dots ,a_{j-1},r\cdot v+w,a_{j+1},\dots ,a_{n}|\\&=r\cdot |a_{1},\dots ,v,\dots a_{n}|+|a_{1},\dots ,w,\dots ,a_{n}|\end{aligned}}$

6. Определитель является чередующимся : всякий раз, когда два столбца матрицы идентичны, ее определитель равен 0:

   $|a_{1},\dots ,v,\dots ,v,\dots ,a_{n}|=0.$

Если определитель определен с использованием формулы Лейбница, как указано выше, эти три свойства можно доказать путем непосредственного изучения этой формулы. Некоторые авторы также подходят к определителю напрямую, используя эти три свойства: можно показать, что существует ровно одна функция, которая присваивает любому $n\times n$-матрица A — число, удовлетворяющее этим трем свойствам. Это также показывает, что этот более абстрактный подход к определителю дает то же определение, что и подход с использованием формулы Лейбница.

Чтобы убедиться в этом, достаточно разложить определитель по многолинейности по столбцам в (огромную) линейную комбинацию определителей матриц, в которой каждый столбец является стандартным базисным вектором. Эти определители равны либо 0 (по свойству 9), либо ±1 (по свойствам 1 и 12 ниже), поэтому линейная комбинация дает приведенное выше выражение в терминах символа Леви-Чивита. Хотя эта характеристика выглядит менее технической, она не может полностью заменить формулу Лейбница при определении определителя, поскольку без нее неясно существование соответствующей функции.

Непосредственные последствия

Эти правила имеют несколько дополнительных последствий:

• Определитель является однородной функцией , т. е.
  $$\det(cA)=c^{n}\det(A)$$
  (для $n\times n$ матрица $A$).
• Перестановка любой пары столбцов матрицы приводит к умножению ее определителя на −1. Это следует из того, что определитель полилинейный и знакопеременный (свойства 2 и 3 выше):
  $$|a_{1},\dots ,a_{j},\dots a_{i},\dots ,a_{n}|=-|a_{1},\dots ,a_{i},\dots ,a_{j},\dots ,a_{n}|.$$
  Эту формулу можно применять итеративно при замене нескольких столбцов. Например
  $$|a_{3},a_{1},a_{2},a_{4}\dots ,a_{n}|=-|a_{1},a_{3},a_{2},a_{4},\dots ,a_{n}|=|a_{1},a_{2},a_{3},a_{4},\dots ,a_{n}|.$$
  В более общем смысле любая перестановка столбцов умножает определитель на знак перестановки.
• Если некоторый столбец может быть выражен как линейная комбинация других столбцов (т. е. столбцы матрицы образуют линейно зависимое множество), определитель равен 0. В особых случаях это включает в себя: если некоторый столбец таков, что все его элементы равны нулю, то определитель этой матрицы равен 0.
• Добавление скаляра, кратного одному столбцу, к другому столбцу не меняет значение определителя. Это следствие полилинейности и альтернативности: в результате полилинейности определитель изменяется кратно определителю матрицы с двумя равными столбцами, определитель которой равен 0, поскольку определитель чередующийся.
• Если $A$ является треугольной матрицей , т.е. $a_{ij}=0$, в любое время $i>j$ или, альтернативно, всякий раз, когда $i<j$, то его определитель равен произведению диагональных элементов:
  $$\det(A)=a_{11}a_{22}\cdots a_{nn}=\prod _{i=1}^{n}a_{ii}.$$
  Действительно, такую ​​матрицу можно сократить, соответствующим образом добавив кратные столбцы с меньшим количеством ненулевых элементов к столбцам с большим количеством элементов, до диагональной матрицы (без изменения определителя). Для такой матрицы использование линейности в каждом столбце сводится к единичной матрице, и в этом случае заявленная формула справедлива по самому первому характеризующему свойству определителей. Альтернативно, эту формулу также можно вывести из формулы Лейбница, поскольку единственная перестановка $\sigma$ которая дает ненулевой вклад, является тождественной перестановкой.

Пример

Эти характеризующие свойства и их последствия, перечисленные выше, являются теоретически значимыми, но также могут быть использованы для вычисления определителей для конкретных матриц. Фактически, метод исключения Гаусса можно применить для приведения любой матрицы к верхнетреугольной форме, и шаги этого алгоритма контролируемым образом влияют на определитель. Следующий конкретный пример иллюстрирует вычисление определителя матрицы $A$ используя этот метод:

$A={\begin{bmatrix}-2&-1&2\\2&1&4\\-3&3&-1\end{bmatrix}}.$

Вычисление определителя матрицы $A$

Матрица	$B={\begin{bmatrix}-3&-1&2\\3&1&4\\0&3&-1\end{bmatrix}}$	$C={\begin{bmatrix}-3&5&2\\3&13&4\\0&0&-1\end{bmatrix}}$	$D={\begin{bmatrix}5&-3&2\\13&3&4\\0&0&-1\end{bmatrix}}$	$E={\begin{bmatrix}18&-3&2\\0&3&4\\0&0&-1\end{bmatrix}}$
Получено	добавить второй столбец к первому	прибавьте 3 раза третий столбец ко второму	поменять местами первые два столбца	добавлять $-{\frac {13}{3}}$ умножить второй столбец на первый
Определитель	$|A|=|B|$	$|B|=|C|$	$|D|=-|C|$	$|E|=|D|$

Объединение этих равенств дает $|A|=-|E|=-(18\cdot 3\cdot (-1))=54.$

Транспонировать

Определитель транспонирования ​ $A$ равен определителю A :

$\det \left(A^{\textsf {T}}\right)=\det(A)$.

Это можно доказать, исследуя формулу Лейбница. Это означает, что во всех упомянутых выше свойствах слово «столбец» можно заменить словом «строка». Например, если рассматривать матрицу размера n × n как состоящую из n строк, то определитель представляет собой n -линейную функцию.

Мультипликативность и группы матриц

Определитель является мультипликативным отображением , т. е. для квадратных матриц $A$ и $B$ одинакового размера, определитель матричного произведения равен произведению их определителей:

$\det(AB)=\det(A)\det(B)$

Этот ключевой факт можно доказать, заметив, что для фиксированной матрицы $B$, обе части уравнения знакопеременные и полилинейные как функция, зависящая от столбцов $A$. Более того, они оба принимают значение $\det B$ когда $A$является единичной матрицей. Таким образом, вышеупомянутая уникальная характеристика чередующихся полилинейных отображений подтверждает это утверждение.

Матрица $A$с записями в поле обратима именно в том случае , если его определитель не равен нулю. Это следует из мультипликативности определителя и формулы обратного преобразования с участием сопряженной матрицы, упомянутой ниже. В этом случае определитель обратной матрицы определяется выражением

$\det \left(A^{-1}\right)={\frac {1}{\det(A)}}=[\det(A)]^{-1}$.

В частности, этим свойством по-прежнему обладают произведения и обратные матрицы с ненулевым определителем (соответственно, определителем). Таким образом, набор таких матриц (фиксированного размера $n$ над полем $K$) образует группу, известную как общая линейная группа $\operatorname {GL} _{n}(K)$ (соответственно подгруппа , называемая специальной линейной группой $\operatorname {SL} _{n}(K)\subset \operatorname {GL} _{n}(K)$. В более общем смысле слово «специальный» обозначает подгруппу другой матричной группы матриц определителя. Примеры включают специальную ортогональную группу (которая, если n равно 2 или 3, состоит из всех матриц вращения ) и специальную унитарную группу .

Поскольку определитель допускает умножение и обратное, на самом деле это гомоморфизм группы из $\operatorname {GL} _{n}(K)$ в мультипликативную группу $K^{\times }$ ненулевых элементов $K$. Этот гомоморфизм сюръективен, и его ядро ​​есть $\operatorname {SL} _{n}(K)$(матрицы с определителем один). Следовательно, по первой теореме об изоморфизме это показывает, что $\operatorname {SL} _{n}(K)$ является нормальной подгруппой $\operatorname {GL} _{n}(K)$, и что факторгруппа $\operatorname {GL} _{n}(K)/\operatorname {SL} _{n}(K)$ изоморфен $K^{\times }$.

Формула Коши-Бине является обобщением этой формулы произведения для прямоугольных матриц. Эту формулу также можно преобразовать в мультипликативную формулу для составных матриц , элементы которых являются определителями всех квадратичных подматриц данной матрицы.

Расширение Лапласа

Разложение Лапласа выражает определитель матрицы $A$ рекурсивно в терминах определителей меньших матриц, известных как их миноры . Несовершеннолетний $M_{i,j}$ определяется как определитель $(n-1)\times (n-1)$-матрица, которая получается из $A$ путем удаления $i$-й ряд и $j$-й столбец. Выражение $(-1)^{i+j}M_{i,j}$известен как кофактор . Для каждого $i$, имеет место равенство

$\det(A)=\sum _{j=1}^{n}(-1)^{i+j}a_{i,j}M_{i,j},$

которое называется разложением Лапласа по i- й строке . Например, разложение Лапласа по первой строке ( $i=1$) дает следующую формулу:

${\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}=a{\begin{vmatrix}e&f\\h&i\end{vmatrix}}-b{\begin{vmatrix}d&f\\g&i\end{vmatrix}}+c{\begin{vmatrix}d&e\\g&h\end{vmatrix}}$

Раскрывая детерминанты этих $2\times 2$-матрицы возвращают упомянутую выше формулу Лейбница. Аналогично, разложение Лапласа вдоль $j$-й столбец равенство

$\det(A)=\sum _{i=1}^{n}(-1)^{i+j}a_{i,j}M_{i,j}.$

Разложение Лапласа можно использовать итеративно для вычисления определителей, но этот подход неэффективен для больших матриц. Однако это полезно для вычисления определителей высокосимметричных матриц, таких как матрица Вандермонда.

$${\begin{vmatrix}1&1&1&\cdots &1\\x_{1}&x_{2}&x_{3}&\cdots &x_{n}\\x_{1}^{2}&x_{2}^{2}&x_{3}^{2}&\cdots &x_{n}^{2}\\\vdots &\vdots &\vdots &\ddots &\vdots \\x_{1}^{n-1}&x_{2}^{n-1}&x_{3}^{n-1}&\cdots &x_{n}^{n-1}\end{vmatrix}}=\prod _{1\leq i<j\leq n}\left(x_{j}-x_{i}\right).$$

-членное разложение n Лапласа по строке или столбцу можно обобщить , записав определитель размера n x n в виде суммы ${\tbinom {n}{k}}$ члены , каждый из которых является произведением определителя подматрицы x k и k определителя дополнительной подматрицы ( n−k ) x ( n−k ).

Матрица адъюгатов

Сопряженная матрица $\operatorname {adj} (A)$ является транспонированием матрицы кофакторов, то есть

$(\operatorname {adj} (A))_{i,j}=(-1)^{i+j}M_{ji}.$

Для каждой матрицы имеется

$(\det A)I=A\operatorname {adj} A=(\operatorname {adj} A)\,A.$

Таким образом, сопряженную матрицу можно использовать для выражения обратной неособой матрицы :

$A^{-1}={\frac {1}{\det A}}\operatorname {adj} A.$

Блочные матрицы

Формула определителя а $2\times 2$-матрица, приведенная выше, продолжает выполняться при соответствующих дальнейших предположениях для блочной матрицы , т. е. матрицы, состоящей из четырех подматриц. $A,B,C,D$ размера $m\times m$, $m\times n$, $n\times m$ и $n\times n$, соответственно. Самая простая такая формула, которую можно доказать с помощью формулы Лейбница или факторизации с дополнением Шура , имеет вид

$\det {\begin{pmatrix}A&0\\C&D\end{pmatrix}}=\det(A)\det(D)=\det {\begin{pmatrix}A&B\\0&D\end{pmatrix}}.$

Если $A$ обратима что , то из результатов раздела о мультипликативности следует,

${\begin{aligned}\det {\begin{pmatrix}A&B\\C&D\end{pmatrix}}&=\det(A)\det {\begin{pmatrix}A&B\\C&D\end{pmatrix}}\underbrace {\det {\begin{pmatrix}A^{-1}&-A^{-1}B\\0&I_{n}\end{pmatrix}}} _{=\,\det(A^{-1})\,=\,(\det A)^{-1}}\\&=\det(A)\det {\begin{pmatrix}I_{m}&0\\CA^{-1}&D-CA^{-1}B\end{pmatrix}}\\&=\det(A)\det(D-CA^{-1}B),\end{aligned}}$

что упрощается до $\det(A)(D-CA^{-1}B)$ когда $D$ это $1\times 1$-матрица.

Аналогичный результат имеет место, когда $D$ обратима, а именно

${\begin{aligned}\det {\begin{pmatrix}A&B\\C&D\end{pmatrix}}&=\det(D)\det {\begin{pmatrix}A&B\\C&D\end{pmatrix}}\underbrace {\det {\begin{pmatrix}I_{m}&0\\-D^{-1}C&D^{-1}\end{pmatrix}}} _{=\,\det(D^{-1})\,=\,(\det D)^{-1}}\\&=\det(D)\det {\begin{pmatrix}A-BD^{-1}C&BD^{-1}\\0&I_{n}\end{pmatrix}}\\&=\det(D)\det(A-BD^{-1}C).\end{aligned}}$

Оба результата можно объединить, чтобы вывести определяющую теорему Сильвестра , которая также изложена ниже.

Если блоки представляют собой квадратные матрицы одинакового размера , дальнейшие формулы справедливы. Например, если $C$ и $D$ ездить на работу (т.е. $CD=DC$), затем

$\det {\begin{pmatrix}A&B\\C&D\end{pmatrix}}=\det(AD-BC).$

Эта формула была обобщена на матрицы, состоящие из более чем $2\times 2$ блоков, опять же при соответствующих условиях коммутативности между отдельными блоками.

Для $A=D$ и $B=C$, справедлива следующая формула (даже если $A$ и $B$ не ездить на работу)

$\det {\begin{pmatrix}A&B\\B&A\end{pmatrix}}=\det(A-B)\det(A+B).$

Определяющая теорема Сильвестра

Детерминантная теорема Сильвестра утверждает, что для A — матрица m × n , а для B — матрица n × m (так что A и B имеют размеры, позволяющие их умножать в любом порядке, образуя квадратную матрицу):

$\det \left(I_{\mathit {m}}+AB\right)=\det \left(I_{\mathit {n}}+BA\right),$

где I _m и I _n — единичные матрицы m × m и n × n соответственно.

Из этого общего результата вытекает несколько следствий.

1. Для случая вектора-столбца c и вектора-строки r , каждый из которых имеет m компонентов, формула позволяет быстро вычислить определитель матрицы, которая отличается от единичной матрицы на матрицу ранга 1:

   $\det \left(I_{\mathit {m}}+cr\right)=1+rc.$

2. В более общем смысле, для любой обратимой размера m × m матрицы X ,
   $\det(X+AB)=\det(X)\det \left(I_{\mathit {n}}+BX^{-1}A\right),$
3. Для вектора-столбца и строки, как указано выше:
   $\det(X+cr)=\det(X)\det \left(1+rX^{-1}c\right)=\det(X)+r\,\operatorname {adj} (X)\,c.$
4. Для квадратных матриц $A$ и $B$ одинакового размера матрицы $AB$ и $BA$ имеют одинаковые характеристические полиномы (следовательно, одинаковые собственные значения).

Сумма

Определитель суммы $A+B$ вообще говоря, не выражается через определители A и B. двух квадратных матриц одинакового размера , Однако для положительных полуопределенных матриц $A$, $B$ и $C$ одинакового размера,

$$\det(A+B+C)+\det(C)\geq \det(A+C)+\det(B+C){\text{,}}$$

с следствием

$$\det(A+B)\geq \det(A)+\det(B){\text{.}}$$

И наоборот, если $A$ и $B$ являются эрмитовыми , положительно определенными и размером $n\times n$, то определитель имеет вогнутую форму $n$^й корень; Из этого следует

$${\sqrt[{n}]{\det {\!(A+B)}}}\geq {\sqrt[{n}]{\det {\!(A)}}}+{\sqrt[{n}]{\det {\!(B)}}}$$

по однородности.

Тождество суммы для матриц 2×2

Для частного случая $2\times 2$ матриц с комплексными элементами определитель суммы можно записать через определители и следы в следующем тождестве:

$\det(A+B)=\det(A)+\det(B)+{\text{tr}}(A){\text{tr}}(B)-{\text{tr}}(AB).$

Удостоверение личности

Это можно показать, расписав каждый термин по компонентам. $A_{ij},B_{ij}$. Левая сторона

$(A_{11}+B_{11})(A_{22}+B_{22})-(A_{12}+B_{12})(A_{21}+B_{21}).$

Расширение дает

$A_{11}A_{22}+B_{11}A_{22}+A_{11}B_{22}+B_{11}B_{22}-A_{12}A_{21}-B_{12}A_{21}-A_{12}B_{21}-B_{12}B_{21}.$

Члены, являющиеся квадратичными по $A$ считаются $\det(A)$, и аналогично для $B$, поэтому выражение можно записать

$\det(A)+\det(B)+A_{11}B_{22}+B_{11}A_{22}-A_{12}B_{21}-B_{12}A_{21}.$

Тогда мы можем записать перекрестные члены как

$(A_{11}+A_{22})(B_{11}+B_{22})-(A_{11}B_{11}+A_{12}B_{21}+A_{21}B_{12}+A_{22}B_{22})$

который можно признать

${\text{tr}}(A){\text{tr}}(B)-{\text{tr}}(AB).$

что завершает доказательство.

У этого есть приложение $2\times 2$матричные алгебры. Например, рассмотрим комплексные числа как матричную алгебру. Комплексные числа имеют представление в виде матриц вида

$$aI+b\mathbf {i} :=a{\begin{pmatrix}1&0\\0&1\end{pmatrix}}+b{\begin{pmatrix}0&-1\\1&0\end{pmatrix}}$$

с $a$ и $b$настоящий. С ${\text{tr}}(\mathbf {i} )=0$, принимая $A=aI$ и $B=b\mathbf {i}$ в приведенном выше тождестве дает

$\det(aI+b\mathbf {i} )=a^{2}\det(I)+b^{2}\det(\mathbf {i} )=a^{2}+b^{2}.$

Этот результат следует только из ${\text{tr}}(\mathbf {i} )=0$ и $\det(I)=\det(\mathbf {i} )=1$.

Свойства определителя по отношению к другим понятиям

Собственные значения и характеристический полином

Определитель тесно связан с двумя другими центральными понятиями линейной алгебры: собственными значениями и характеристическим многочленом матрицы. Позволять $A$ быть $n\times n$-матрица со сложными элементами. Тогда по основной теореме алгебры $A$ должно иметь ровно n собственных значений $\lambda _{1},\lambda _{2},\ldots ,\lambda _{n}$. (Здесь подразумевается, что собственное значение с алгебраической кратностью µ встречается в этом списке µ раз.) Тогда оказывается, что определитель A равен произведению этих собственных значений:

$\det(A)=\prod _{i=1}^{n}\lambda _{i}=\lambda _{1}\lambda _{2}\cdots \lambda _{n}.$

Произведение всех ненулевых собственных значений называется псевдодетерминантом .

Отсюда сразу видно, что определитель матрицы $A$ равен нулю тогда и только тогда, когда $0$ является собственным значением $A$. Другими словами, $A$ обратима тогда и только тогда, когда $0$ не является собственным значением $A$.

Характеристический полином определяется как

$\chi _{A}(t)=\det(t\cdot I-A).$

Здесь, $t$ является неопределенным многочлена и $I$ - единичная матрица того же размера, что и $A$. С помощью этого полинома определители можно использовать для нахождения собственных значений матрицы $A$: они и являются корнями этого многочлена, т. е. теми комплексными числами $\lambda$ такой, что

$\chi _{A}(\lambda )=0.$

Эрмитова матрица является положительно определенной, если все ее собственные значения положительны. Критерий Сильвестра утверждает, что это эквивалентно определителям подматриц.

$A_{k}:={\begin{bmatrix}a_{1,1}&a_{1,2}&\cdots &a_{1,k}\\a_{2,1}&a_{2,2}&\cdots &a_{2,k}\\\vdots &\vdots &\ddots &\vdots \\a_{k,1}&a_{k,2}&\cdots &a_{k,k}\end{bmatrix}}$

быть позитивным для всех $k$ между $1$ и $n$.

След

След tr ( A ) по определению является суммой диагональных элементов A , а также суммой собственных значений. Таким образом, для комплексных матриц A ,

$\det(\exp(A))=\exp(\operatorname {tr} (A))$

или, для вещественных матриц A ,

$\operatorname {tr} (A)=\log(\det(\exp(A))).$

Здесь exp( A ) обозначает матричную экспоненту A A , поскольку каждое собственное значение λ соответствует A собственному значению exp( λ ) exp( ) . В частности, для любого логарифма A , , то есть любой матрицы L удовлетворяющей

$\exp(L)=A$

определитель A определяется выражением

$\det(A)=\exp(\operatorname {tr} (L)).$

Например, для n = 2 , n = 3 и n = 4 соответственно,

${\begin{aligned}\det(A)&={\frac {1}{2}}\left(\left(\operatorname {tr} (A)\right)^{2}-\operatorname {tr} \left(A^{2}\right)\right),\\\det(A)&={\frac {1}{6}}\left(\left(\operatorname {tr} (A)\right)^{3}-3\operatorname {tr} (A)~\operatorname {tr} \left(A^{2}\right)+2\operatorname {tr} \left(A^{3}\right)\right),\\\det(A)&={\frac {1}{24}}\left(\left(\operatorname {tr} (A)\right)^{4}-6\operatorname {tr} \left(A^{2}\right)\left(\operatorname {tr} (A)\right)^{2}+3\left(\operatorname {tr} \left(A^{2}\right)\right)^{2}+8\operatorname {tr} \left(A^{3}\right)~\operatorname {tr} (A)-6\operatorname {tr} \left(A^{4}\right)\right).\end{aligned}}$

ср. Теорема Кэли-Гамильтона . Такие выражения выводятся из комбинаторных аргументов, тождеств Ньютона или алгоритма Фаддеева-Леверье . То есть для общего det n A = (−1) ^н c ₀ — постоянный член характеристического многочлена со знаком , определяемый рекурсивно из

$c_{n}=1;~~~c_{n-m}=-{\frac {1}{m}}\sum _{k=1}^{m}c_{n-m+k}\operatorname {tr} \left(A^{k}\right)~~(1\leq m\leq n)~.$

В общем случае это также можно получить из

$\det(A)=\sum _{\begin{array}{c}k_{1},k_{2},\ldots ,k_{n}\geq 0\\k_{1}+2k_{2}+\cdots +nk_{n}=n\end{array}}\prod _{l=1}^{n}{\frac {(-1)^{k_{l}+1}}{l^{k_{l}}k_{l}!}}\operatorname {tr} \left(A^{l}\right)^{k_{l}},$

где сумма берется по множеству всех целых чисел k _l ≥ 0, удовлетворяющих уравнению

$\sum _{l=1}^{n}lk_{l}=n.$

Формулу можно выразить через полный экспоненциальный полином Белла от n аргументов s _l = −( l – 1)! tr( А ^л ) как

$\det(A)={\frac {(-1)^{n}}{n!}}B_{n}(s_{1},s_{2},\ldots ,s_{n}).$

Эту формулу также можно использовать для нахождения определителя матрицы A ^я _J с многомерными индексами I знак равно ( я ₁ , я ₂ , ..., я _р ) и J знак равно ( j ₁ , j ₂ , ..., j _р ) . Произведение и след таких матриц естественным образом определяются как

$(AB)_{J}^{I}=\sum _{K}A_{K}^{I}B_{J}^{K},\operatorname {tr} (A)=\sum _{I}A_{I}^{I}.$

Важное тождество произвольной размерности n можно получить из разложения логарифма в ряд Меркатора , когда разложение сходится. Если каждое собственное значение A меньше 1 по абсолютной величине,

$\det(I+A)=\sum _{k=0}^{\infty }{\frac {1}{k!}}\left(-\sum _{j=1}^{\infty }{\frac {(-1)^{j}}{j}}\operatorname {tr} \left(A^{j}\right)\right)^{k}\,,$

где I — единичная матрица. В более общем смысле, если

$\sum _{k=0}^{\infty }{\frac {1}{k!}}\left(-\sum _{j=1}^{\infty }{\frac {(-1)^{j}s^{j}}{j}}\operatorname {tr} \left(A^{j}\right)\right)^{k}\,,$

разлагается в формальный степенной ряд по s, тогда все коэффициенты s ^м для m > n равны нулю, а оставшийся многочлен равен det( I + sA ) .

Верхняя и нижняя границы

Для положительно определенной матрицы A оператор следа дает следующие точные нижние и верхние границы логарифмического определителя:

$\operatorname {tr} \left(I-A^{-1}\right)\leq \log \det(A)\leq \operatorname {tr} (A-I)$

с равенством тогда и только тогда, A = I. когда Эту взаимосвязь можно вывести с помощью формулы расхождения Кульбака-Лейблера между двумя многомерными нормальными распределениями.

Также,

${\frac {n}{\operatorname {tr} \left(A^{-1}\right)}}\leq \det(A)^{\frac {1}{n}}\leq {\frac {1}{n}}\operatorname {tr} (A)\leq {\sqrt {{\frac {1}{n}}\operatorname {tr} \left(A^{2}\right)}}.$

Эти неравенства можно доказать, выразив следы и определитель через собственные значения. По сути, они отражают хорошо известный факт, что среднее гармоническое меньше среднего геометрического , которое меньше среднего арифметического , которое, в свою очередь, меньше среднеквадратического .

Производная

Формула Лейбница показывает, что определитель вещественных (или аналогично комплексных) квадратных матриц является полиномиальной функцией от $\mathbf {R} ^{n\times n}$ к $\mathbf {R}$. В частности, оно всюду дифференцируемо . Его производную можно выразить по формуле Якоби :

${\frac {d\det(A)}{d\alpha }}=\operatorname {tr} \left(\operatorname {adj} (A){\frac {dA}{d\alpha }}\right).$

где $\operatorname {adj} (A)$ обозначает сопряжение ​ $A$. В частности, если $A$ обратимо, мы имеем

${\frac {d\det(A)}{d\alpha }}=\det(A)\operatorname {tr} \left(A^{-1}{\frac {dA}{d\alpha }}\right).$

Выражается в виде записей $A$, это

${\frac {\partial \det(A)}{\partial A_{ij}}}=\operatorname {adj} (A)_{ji}=\det(A)\left(A^{-1}\right)_{ji}.$

Еще одна эквивалентная формулировка:

$\det(A+\epsilon X)-\det(A)=\operatorname {tr} (\operatorname {adj} (A)X)\epsilon +O\left(\epsilon ^{2}\right)=\det(A)\operatorname {tr} \left(A^{-1}X\right)\epsilon +O\left(\epsilon ^{2}\right)$,

используя большое обозначение O. Особый случай, когда $A=I$, единичная матрица, дает

$\det(I+\epsilon X)=1+\operatorname {tr} (X)\epsilon +O\left(\epsilon ^{2}\right).$

Это тождество используется при описании алгебр Ли, ассоциированных с некоторыми матричными группами Ли . Например, специальная линейная группа $\operatorname {SL} _{n}$ определяется уравнением $\det A=1$. Приведенная выше формула показывает, что ее алгебра Ли является специальной линейной алгеброй Ли. ${\mathfrak {sl}}_{n}$ состоящая из матриц, имеющих нулевой след.

Написание $3\times 3$-матрица как $A={\begin{bmatrix}a&b&c\end{bmatrix}}$ где $a,b,c$ являются векторами-столбцами длины 3, то градиент по одному из трех векторов можно записать как векторное произведение двух других:

${\begin{aligned}\nabla _{\mathbf {a} }\det(A)&=\mathbf {b} \times \mathbf {c} \\\nabla _{\mathbf {b} }\det(A)&=\mathbf {c} \times \mathbf {a} \\\nabla _{\mathbf {c} }\det(A)&=\mathbf {a} \times \mathbf {b} .\end{aligned}}$

История

Исторически определители использовались задолго до появления матриц: изначально определитель определялся как свойство системы линейных уравнений . Определитель «определяет», имеет ли система единственное решение (что происходит именно в том случае, если определитель не равен нулю). В этом смысле определители были впервые использованы в китайском учебнике математики «Девять глав математического искусства» (九章算術, китайские учёные, около III века до нашей эры). В Европе решения линейных систем двух уравнений были выражены Кардано в 1545 году с помощью сущности, похожей на определитель.

Собственно определители возникли отдельно от работы Секи Такакадзу в 1683 г. в Японии и параллельно Лейбница в 1693 г. Крамер (1750) без доказательств сформулировал правило Крамера. И Крамер, и Безу (1779) пришли к определителям благодаря вопросу о плоских кривых , проходящих через заданный набор точек.

Вандермонд (1771) впервые признал детерминанты независимыми функциями. Лаплас (1772) дал общий метод разложения определителя по дополнительным минорам : Вандермонд уже привел частный случай. Сразу после этого Лагранж (1773) рассмотрел определители второго и третьего порядка и применил их к вопросам теории исключения ; он доказал множество частных случаев общих тождеств.

Гаусс (1801 г.) сделал следующий шаг. Как и Лагранж, он широко использовал определители в теории чисел . Он ввел слово «определитель» (Лаплас использовал слово «результат»), но не в его нынешнем значении, а скорее применительно дискриминанту кванта к . Гаусс также пришел к понятию обратных (обратных) определителей и очень близко подошел к теореме умножения.

Следующим важным вкладчиком является Бине (1811, 1812), который формально сформулировал теорему о произведении двух матриц из m столбцов и n строк, которая для частного случая m = n сводится к теореме умножения. В тот же день (30 ноября 1812 г.), когда Бине представил свою статью Академии, Коши также представил доклад на эту тему. (См. формулу Коши – Бине .) Здесь он использовал слово «детерминант» в его нынешнем смысле: обобщил и упростил то, что тогда было известно по этому вопросу, улучшил обозначения и дал теорему умножения с доказательством, более удовлетворительным, чем у Бине. С него начинается теория в ее общности.

Якоби (1841) использовал функциональный определитель, который Сильвестр позже назвал якобианом . В своих мемуарах в «Журнале Крелля» за 1841 год он специально рассматривает этот предмет, а также класс знакопеременных функций, которые Сильвестр назвал альтернативами . Примерно во время последних мемуаров Якоби Сильвестр (1839 г.) и Кэли начали свою работу. Кэли в 1841 году ввел современное обозначение определителя с помощью вертикальных черт.

Изучение специальных форм определителей явилось естественным результатом завершения общей теории. Осесимметричные определители изучались Лебегом , Гессе и Сильвестром; персимметричные определители Сильвестра и Ханкеля ; циркулянты Каталана , , Споттисвуда Глейшера и Скотта; косые определители и пфаффианы , в связи с теорией ортогональных преобразований , Кэли; продолжатели Сильвестра; Вронскианы (так называемые Мьюиром ) Кристоффеля и Фробениуса ; составные определители Сильвестра, Рейсса и Пике; Якобианы и гессианцы Сильвестра; и симметричные определители гош Труди . Из учебников по этому предмету первым был учебник Споттисвуда. В Америке трактаты опубликовали Ханус (1886 г.), Уэлд (1893 г.) и Мьюир / Мецлер (1933 г.).

Приложения

Правило Крамера

Определители можно использовать для описания решений линейной системы уравнений , записанной в матричной форме как $Ax=b$. Это уравнение имеет единственное решение $x$ если и только если $\det(A)$ненулевое значение. В этом случае решение дается по правилу Крамера :

$x_{i}={\frac {\det(A_{i})}{\det(A)}}\qquad i=1,2,3,\ldots ,n$

где $A_{i}$ – матрица, образованная заменой $i$-й столбец $A$ по вектор-столбцу $b$. Это немедленно следует из разложения определителя по столбцу, т. е.

$\det(A_{i})=\det {\begin{bmatrix}a_{1}&\ldots &b&\ldots &a_{n}\end{bmatrix}}=\sum _{j=1}^{n}x_{j}\det {\begin{bmatrix}a_{1}&\ldots &a_{i-1}&a_{j}&a_{i+1}&\ldots &a_{n}\end{bmatrix}}=x_{i}\det(A)$

где векторы $a_{j}$являются столбцами A . Правило также подразумевается тождеством

$A\,\operatorname {adj} (A)=\operatorname {adj} (A)\,A=\det(A)\,I_{n}.$

Правило Крамера может быть реализовано в $\operatorname {O} (n^{3})$ время, что сравнимо с более распространенными методами решения систем линейных уравнений, такими как LU , QR или разложение по сингулярным значениям .

Линейная независимость

Определители можно использовать для характеристики линейно зависимых векторов: $\det A$ равен нулю тогда и только тогда, когда векторы-столбцы (или, что то же самое, векторы-строки) матрицы $A$ линейно зависимы. Например, даны два линейно независимых вектора $v_{1},v_{2}\in \mathbf {R} ^{3}$, третий вектор $v_{3}$ лежит в плоскости , натянутой на первые два вектора, точно, если определитель $3\times 3$-матрица, состоящая из трех векторов, равна нулю. Та же идея используется и в теории дифференциальных уравнений : заданные функции $f_{1}(x),\dots ,f_{n}(x)$ (должно быть $n-1$ раз дифференцируемо ), вронскиан определяется как

$W(f_{1},\ldots ,f_{n})(x)={\begin{vmatrix}f_{1}(x)&f_{2}(x)&\cdots &f_{n}(x)\\f_{1}'(x)&f_{2}'(x)&\cdots &f_{n}'(x)\\\vdots &\vdots &\ddots &\vdots \\f_{1}^{(n-1)}(x)&f_{2}^{(n-1)}(x)&\cdots &f_{n}^{(n-1)}(x)\end{vmatrix}}.$

Оно не равно нулю (для некоторых $x$) в заданном интервале тогда и только тогда, когда заданные функции и все их производные до порядка $n-1$линейно независимы. Если можно показать, что вронскиан равен нулю всюду на интервале, то в случае аналитических функций это означает, что данные функции линейно зависимы. См. вронскиан и линейную независимость . Другим примером использования определителя является результирующая , которая дает критерий, когда два многочлена имеют общий корень .

Ориентация основы

Основная статья: Ориентация (векторное пространство)

Определитель можно рассматривать как присвоение номера каждой последовательности из n векторов в R. ^н , используя квадратную матрицу, столбцы которой являются заданными векторами. Определитель будет отличен от нуля тогда и только тогда, когда последовательность векторов является базой для R ^н . В этом случае знак определителя определяет, согласуется ли ориентация базиса с ориентацией стандартного базиса или противоположна ему . В случае ортогонального базиса величина определителя равна произведению длин базисных векторов. Например, ортогональная матрица с элементами в R ^н представляет собой ортонормированный базис в евклидовом пространстве и, следовательно, имеет определитель ±1 (поскольку все векторы имеют длину 1). Определитель равен +1 тогда и только тогда, когда базис имеет ту же ориентацию. Оно равно −1 тогда и только тогда, когда базис имеет противоположную ориентацию.

В более общем смысле, если определитель A положителен, A , сохраняющее ориентацию представляет собой линейное преобразование (если A — ортогональная матрица 2 × 2 или 3 × 3 , это вращение ), а если он отрицательный, A меняет ориентацию. основы.

объема

Как указывалось выше, абсолютное значение определителя вещественных векторов равно объему параллелепипеда, натянутого на эти векторы. Как следствие, если $f:\mathbf {R} ^{n}\to \mathbf {R} ^{n}$ - линейное отображение, заданное умножением на матрицу $A$, и $S\subset \mathbf {R} ^{n}$ — любое измеримое подмножество , то объём $f(S)$ дан кем-то $|\det(A)|$ раз больше объёма $S$. В более общем смысле, если линейное отображение $f:\mathbf {R} ^{n}\to \mathbf {R} ^{m}$ представлен $m\times n$-матрица $A$, тогда $n$- габаритный объем $f(S)$ дан кем-то:

$\operatorname {volume} (f(S))={\sqrt {\det \left(A^{\textsf {T}}A\right)}}\operatorname {volume} (S).$

Вычислив объем тетраэдра, ограниченного четырьмя точками, их можно использовать для выявления перекосов линий . Объем любого тетраэдра с учетом его вершин $a,b,c,d$, ${\frac {1}{6}}\cdot |\det(a-b,b-c,c-d)|$или любая другая комбинация пар вершин, образующая связующее дерево по вершинам.

Нелинейная карта $f\colon \mathbf {R} ^{2}\to \mathbf {R} ^{2}$превращает небольшой квадрат (слева, красный) в искаженный параллелограмм (справа, красный). Якобиан в точке дает наилучшую линейную аппроксимацию искаженного параллелограмма вблизи этой точки (справа, полупрозрачный белый цвет), а определитель Якобиана дает отношение площади аппроксимирующего параллелограмма к площади исходного квадрата.

Для общей дифференцируемой функции многое из вышесказанного переносится при рассмотрении матрицы Якоби функции f . Для

$f:\mathbf {R} ^{n}\rightarrow \mathbf {R} ^{n},$

матрица Якобиана представляет собой матрицу размера n × n , элементы которой задаются частными производными

$D(f)=\left({\frac {\partial f_{i}}{\partial x_{j}}}\right)_{1\leq i,j\leq n}.$

Его определитель, определитель Якобиана , появляется в многомерной версии интегрирования путем замены : для подходящих функций f и открытого подмножества U в R ^н (область определения f ), интеграл по f ( U ) от некоторой другой функции φ : R ^н → Р ^м дан кем-то

$\int _{f(U)}\phi (\mathbf {v} )\,d\mathbf {v} =\int _{U}\phi (f(\mathbf {u} ))\left|\det(\operatorname {D} f)(\mathbf {u} )\right|\,d\mathbf {u} .$

Якобиан также встречается в теореме об обратной функции .

Применительно к области картографии определитель можно использовать для измерения скорости расширения карты вблизи полюсов.

Абстрактные

Определитель эндоморфизма

Из приведенных выше тождеств, касающихся определителя произведений и обратных матриц, следует, что подобные матрицы имеют один и тот же определитель: две матрицы A и B подобны, если существует обратимая матрица X такая, что A = X ⁻¹ БХ . Действительно, повторное применение приведенных выше тождеств дает

$\det(A)=\det(X)^{-1}\det(B)\det(X)=\det(B)\det(X)^{-1}\det(X)=\det(B).$

Поэтому определитель также называют инвариантом подобия . Определитель линейного преобразования

$T:V\to V$

для некоторого конечномерного векторного пространства V определяется как определитель описывающей его матрицы относительно произвольного выбора базиса в V . В силу инвариантности подобия этот определитель не зависит от выбора базиса V и, следовательно, зависит только от эндоморфизма T .

Квадратные матрицы над коммутативными кольцами

Приведенное выше определение определителя с использованием правила Лейбница работает в более общем смысле, когда элементы матрицы являются элементами коммутативного кольца. $R$, например целые числа $\mathbf {Z}$, в отличие от поля действительных или комплексных чисел. Более того, характеризация определителя как единственного знакопеременного полилинейного отображения, удовлетворяющего условию $\det(I)=1$ по-прежнему сохраняется, как и все свойства, вытекающие из этой характеристики.

Матрица $A\in \operatorname {Mat} _{n\times n}(R)$ обратима (в том смысле, что существует обратная матрица, элементы которой находятся в $R$) тогда и только тогда, когда его определитель является обратимым элементом в $R$. Для $R=\mathbf {Z}$, это означает, что определитель равен +1 или −1. Такая матрица называется унимодулярной .

Определитель, будучи мультипликативным, определяет групповой гомоморфизм

$\operatorname {GL} _{n}(R)\rightarrow R^{\times },$

между общей линейной группой (группой обратимых $n\times n$-матрицы с записями в $R$) и мультипликативная группа единиц в $R$. Поскольку оно соблюдает умножение в обеих группах, это отображение является групповым гомоморфизмом .

Определитель представляет собой естественное преобразование.

Учитывая кольцевой гомоморфизм $f:R\to S$, есть карта $\operatorname {GL} _{n}(f):\operatorname {GL} _{n}(R)\to \operatorname {GL} _{n}(S)$ задано заменой всех записей в $R$ по их изображениям под $f$. Определитель учитывает эти отображения, т. е. тождество

$f(\det((a_{i,j})))=\det((f(a_{i,j})))$

держит. Другими словами, отображаемая коммутативная диаграмма коммутирует.

Например, определитель комплексно -сопряженной комплексной матрицы (который также является определителем ее сопряженного транспонирования) является комплексно-сопряженным ее определителем, а для целочисленных матриц: приведение по модулю $m$ определителя такой матрицы равен определителю матрицы, приведенному по модулю $m$(последний определитель вычисляется с использованием модульной арифметики ). На языке теории категорий определитель — это естественное преобразование между двумя функторами. $\operatorname {GL} _{n}$ и $(-)^{\times }$. Добавляя еще один уровень абстракции, это можно выразить, сказав, что определитель является морфизмом алгебраических групп , от общей линейной группы до мультипликативной группы .

$\det :\operatorname {GL} _{n}\to \mathbb {G} _{m}.$

Внешняя алгебра

Смотрите также: Внешняя алгебра § Линейная алгебра

Определитель линейного преобразования $T:V\to V$ из $n$-мерное векторное пространство $V$ или, в более общем смысле, свободный модуль (конечного) ранга $n$ над коммутативным кольцом $R$ можно сформулировать в бескоординатной форме, рассматривая $n$-я внешняя сила $\bigwedge ^{n}V$ из $V$. Карта $T$ индуцирует линейное отображение

${\begin{aligned}\bigwedge ^{n}T:\bigwedge ^{n}V&\rightarrow \bigwedge ^{n}V\\v_{1}\wedge v_{2}\wedge \dots \wedge v_{n}&\mapsto Tv_{1}\wedge Tv_{2}\wedge \dots \wedge Tv_{n}.\end{aligned}}$

Как $\bigwedge ^{n}V$ одномерна, карта $\bigwedge ^{n}T$ задается путем умножения на некоторый скаляр, т. е. элемент в $R$. Некоторые авторы, такие как ( Bourbaki 1998 ), используют этот факт, чтобы определить определитель как элемент в $R$ удовлетворяющее следующему тождеству (для всех $v_{i}\in V$):

$\left(\bigwedge ^{n}T\right)\left(v_{1}\wedge \dots \wedge v_{n}\right)=\det(T)\cdot v_{1}\wedge \dots \wedge v_{n}.$

Это определение согласуется с более конкретным определением, зависящим от координат. Это можно показать, используя единственность полилинейной знакопеременной формы на $n$-кортежи векторов в $R^{n}$. По этой причине самая высокая ненулевая внешняя мощность $\bigwedge ^{n}V$ (в отличие от определителя, связанного с эндоморфизмом) иногда также называют определителем $V$и аналогично для более сложных объектов, таких как векторные расслоения или цепные комплексы векторных пространств. Второстепенные элементы матрицы также можно отобразить в этом случае, рассматривая более низкие чередующиеся формы. $\bigwedge ^{k}V$ с $k<n$.

Обобщения и родственные понятия

Детерминанты, рассмотренные выше, допускают несколько вариантов: перманент матрицы определяется как детерминант, за исключением того, что факторы $\operatorname {sgn}(\sigma )$происходящие в правиле Лейбница, опущены. Имманант обобщает оба , вводя характер симметрической группы. $S_{n}$ в правление Лейбница.

Определители для конечномерных алгебр

Для любой ассоциативной алгебры $A$ конечномерное как векторное пространство над полем $F$, существует определительное отображение

$\det :A\to F.$

Это определение продолжается путем установления характеристического полинома независимо от определителя и определения определителя как члена самого низкого порядка этого многочлена. Это общее определение восстанавливает определитель матричной алгебры $A=\operatorname {Mat} _{n\times n}(F)$, но также включает несколько дополнительных случаев, включая определитель кватерниона ,

$\det(a+ib+jc+kd)=a^{2}+b^{2}+c^{2}+d^{2}$,

норма ​ $N_{L/F}:L\to F$ , расширения поля а также пфаффиан кососимметрической матрицы и приведенная норма центральной простой алгебры также возникают как частные случаи этой конструкции.

Бесконечные матрицы

Для матриц с бесконечным числом строк и столбцов приведенные выше определения определителя не переносятся напрямую. Например, в формуле Лейбница необходимо вычислить бесконечную сумму (все члены которой являются бесконечными произведениями). Функциональный анализ предоставляет различные расширения определителя для таких бесконечномерных ситуаций, которые, однако, работают только для определенных типов операторов.

Определитель Фредгольма определяет определитель для операторов, известных как операторы ядерного класса, посредством соответствующего обобщения формулы

$\det(I+A)=\exp(\operatorname {tr} (\log(I+A))).$

Другое бесконечномерное понятие определителя — функциональный определитель .

Операторы в

Для операторов с конечным фактором можно определить положительный вещественный определитель, называемый определителем Фугледа-Кадисона, используя канонический след. Фактически, каждому состоянию следа в алгебре фон Неймана соответствует понятие определителя Фугледа–Кадисона.

Связанные понятия для некоммутативных колец

Для матриц над некоммутативными кольцами полилинейность и альтернирующие свойства несовместимы при n ≥ 2 , поэтому в этой ситуации нет хорошего определения определителя.

Для квадратных матриц с элементами в некоммутативном кольце возникают различные трудности с определением определителей аналогично тому, как это делается для коммутативных колец. Формуле Лейбница можно придать смысл при условии, что указан порядок произведения, и аналогично для других определений определителя, но некоммутативность тогда приводит к потере многих фундаментальных свойств определителя, таких как мультипликативное свойство или что определитель не изменится при транспонировании матрицы. Над некоммутативными кольцами не существует разумного понятия полилинейной формы (существование ненулевой билинейной формы с регулярным элементом R R в качестве значения некоторой пары аргументов следует, что коммутативен ). Тем не менее, были сформулированы различные понятия некоммутативного определителя, которые сохраняют некоторые свойства определителей, особенно квазидетерминантов и определителя Дьедонне . Для некоторых классов матриц с некоммутативными элементами можно определить определитель и доказать теоремы линейной алгебры, очень похожие на их коммутативные аналоги. Примеры включают q -детерминант на квантовых группах, определитель Капелли на матрицах Капелли и березинский на суперматрицах (т. е. матрицах, элементы которых являются элементами $\mathbb {Z} _{2}$- градуированные кольца ). Матрицы Манина образуют класс, наиболее близкий к матрицам с коммутативными элементами.

Расчет

Определители в основном используются в качестве теоретического инструмента. Они редко вычисляются явно в числовой линейной алгебре , где для таких приложений, как проверка обратимости и поиск собственных значений, определитель в основном вытесняется другими методами. Однако вычислительная геометрия часто использует вычисления, связанные с определителями.

Хотя определитель можно вычислить напрямую с помощью правила Лейбница, этот подход крайне неэффективен для больших матриц, поскольку эта формула требует вычисления $n!$ ( $n$ факториал ) продукция для $n\times n$-матрица. Таким образом, количество требуемых операций растет очень быстро: оно порядка $n!$. Разложение Лапласа также неэффективно. Поэтому для расчета определителей были разработаны более сложные методы.

Методы декомпозиции

Некоторые методы вычисления $\det(A)$записав матрицу как произведение матриц, определители которых легче вычислить. Такие методы называются методами декомпозиции. Примеры включают LU-разложение , QR-разложение или разложение Холецкого (для положительно определенных матриц ). Эти методы имеют порядок $\operatorname {O} (n^{3})$, что является значительным улучшением по сравнению с $\operatorname {O} (n!)$.

Например, LU-разложение выражает $A$ как продукт

$A=PLU.$

матрицы перестановок $P$ (который имеет ровно один $1$ в каждом столбце, а в противном случае нули), нижняя треугольная матрица $L$ и верхняя треугольная матрица $U$. Определители двух треугольных матриц $L$ и $U$могут быть быстро вычислены, поскольку они являются произведениями соответствующих диагональных элементов. Определитель $P$ это просто знак $\varepsilon$ соответствующей перестановки (которая $+1$ для четного числа перестановок и $-1$для нечетного числа перестановок). Как только такое LU-разложение известно для $A$, его определитель легко вычисляется как

$\det(A)=\varepsilon \det(L)\cdot \det(U).$

Дальнейшие методы

Приказ $\operatorname {O} (n^{3})$Достигнутая методами декомпозиции, была улучшена различными методами. Если две матрицы порядка $n$ можно умножить во времени $M(n)$, где $M(n)\geq n^{a}$ для некоторых $a>2$, то существует алгоритм, вычисляющий определитель за время $O(M(n))$. Это означает, например, что $\operatorname {O} (n^{2.376})$Существует алгоритм вычисления определителя, основанный на алгоритме Копперсмита-Винограда . С 2016 года этот показатель был снижен до 2,373.

Помимо сложности алгоритма, для сравнения алгоритмов можно использовать и другие критерии. Специально для приложений, касающихся матриц над кольцами, существуют алгоритмы, вычисляющие определитель без каких-либо делений. (Напротив, исключение Гаусса требует деления.) Один из таких алгоритмов, имеющий сложность $\operatorname {O} (n^{4})$основан на следующей идее: перестановки (как в правиле Лейбница) заменяются так называемыми закрытыми упорядоченными блужданиями , в которых несколько элементов могут повторяться. В полученной сумме больше членов, чем в правиле Лейбница, но в процессе некоторые из этих произведений можно использовать повторно, что делает его более эффективным, чем наивные вычисления по правилу Лейбница. Алгоритмы также можно оценивать по их битовой сложности , т. е. по тому, сколько бит точности необходимо для хранения промежуточных значений, возникающих при вычислении. Например, метод исключения Гаусса (или LU-разложение) имеет порядок $\operatorname {O} (n^{3})$, но длина промежуточных значений в битах может стать экспоненциально большой. Для сравнения, алгоритм Барейсса представляет собой метод точного деления (поэтому он использует деление, но только в тех случаях, когда эти деления могут быть выполнены без остатка) имеет тот же порядок, но битовая сложность примерно равна битовому размеру исходные записи в матричных временах $n$.

Если определитель A и обратное значение A уже вычислены, лемма об определителе матрицы позволяет быстро вычислить определитель A + uv. ^Т , где u и v — векторы-столбцы.

Чарльз Доджсон (т.е. Льюис Кэрролл из «Алисы в стране чудес ») изобрел метод вычисления определителей, названный конденсацией Доджсона . К сожалению, этот интересный метод не всегда работает в исходном виде.

См. также

• Определитель Коши
• Определитель Кэли – Менгера
• Определитель Дьедонне
• Определитель Слейтера
• Детерминантная гипотеза

Ссылки

См. Также: Линейная алгебра § Дополнительная литература

• Антон, Ховард (2005), Элементарная линейная алгебра (версия для приложений) (9-е изд.), Wiley International
• Экслер, Шелдон Джей (2015). Линейная алгебра сделана правильно (3-е изд.). Спрингер . ISBN  978-3-319-11079-0 .
• Барейсс, Эрвин (1968), «Идентичность Сильвестра и многошаговое исключение Гаусса с сохранением целых чисел» (PDF) , Mathematics of Computation , 22 (102): 565–578, doi : 10.2307/2004533 , JSTOR   2004533 , заархивировано (PDF) из оригинал от 25 октября 2012 г.
• де Бур, Карл (1990), «Пустое упражнение» (PDF) , Информационный бюллетень ACM SIGNUM , 25 (2): 3–7, doi : 10.1145/122272.122273 , S2CID   62780452 , заархивировано (PDF) из оригинала в 2006-09 гг. -01
• Бурбаки, Николя (1998), Алгебра I, главы 1–3 , Springer, ISBN  9783540642435
• Банч, младший; Хопкрофт, Дж. Э. (1974). «Треугольная факторизация и инверсия путем быстрого умножения матриц» . Математика вычислений . 28 (125): 231–236. doi : 10.1090/S0025-5718-1974-0331751-8 . hdl : 1813/6003 .
• Даммит, Дэвид С.; Фут, Ричард М. (2004), Абстрактная алгебра (3-е изд.), Хобокен, Нью-Джерси: Wiley, ISBN  9780471452348 , OCLC   248917264
• Фисикопулос, Виссарион; Пеньяранда, Луис (2016), «Быстрые геометрические алгоритмы с помощью динамического вычисления определителей», Computational Geometry , 54 : 1–16, arXiv : 1206.7067 , doi : 10.1016/j.comgeo.2015.12.001
• Гарибальди, Скип (2004), «Характеристический полином и определитель не являются специальными конструкциями», American Mathematical Monthly , 111 (9): 761–778, arXiv : math/0203276 , doi : 10.2307/4145188 , JSTOR   4145188 , MR   2104048
• Хабгуд, Кен; Арел, Итамар (2012). «Применение правила Крамера на основе конденсации для решения крупномасштабных линейных систем» (PDF) . Журнал дискретных алгоритмов . 10 : 98–109. дои : 10.1016/j.jda.2011.06.007 . Архивировано (PDF) из оригинала 5 мая 2019 г.
• Харрис, Фрэнк Э. (2014), Математика для физических наук и техники , Elsevier, ISBN  9780128010495
• Кляйнер, Израиль (2007), Кляйнер, Израиль (ред.), История абстрактной алгебры , Биркхойзер, doi : 10.1007/978-0-8176-4685-1 , ISBN  978-0-8176-4684-4 , МР   2347309
• Кунг, Джозеф PS; Рота, Джан-Карло; Ян, Кэтрин (2009), Комбинаторика: путь Роты , издательство Кембриджского университета, ISBN  9780521883894
• Лэй, Дэвид К. (22 августа 2005 г.), Линейная алгебра и ее приложения (3-е изд.), Аддисон Уэсли, ISBN  978-0-321-28713-7
• Ломбарди, Анри; Китте, Клод (2015), Коммутативная алгебра: конструктивные методы , Springer, ISBN  9789401799447
• Мак Лейн, Сондерс (1998), Категории для работающего математика , Тексты для выпускников по математике 5 (2-е изд.), Springer-Verlag, ISBN  0-387-98403-8
• Мейер, Карл Д. (15 февраля 2001 г.), Матричный анализ и прикладная линейная алгебра , Общество промышленной и прикладной математики (SIAM), ISBN  978-0-89871-454-8 , заархивировано из оригинала 31 октября 2009 г.
• Мьюир, Томас (1960) [1933], Трактат по теории детерминантов , переработанный и дополненный Уильямом Х. Мецлером, Нью-Йорк, штат Нью-Йорк: Дувр
• Пул, Дэвид (2006), Линейная алгебра: современное введение (2-е изд.), Брукс/Коул, ISBN  0-534-99845-3
• Дж. Бейли Прайс (1947) «Некоторые тождества в теории определителей», American Mathematical Monthly 54:75–90 MR 0019078
• Хорн, Роджер Алан ; Джонсон, Чарльз Роял (2018) [1985]. Матричный анализ (2-е изд.). Издательство Кембриджского университета . ISBN  978-0-521-54823-6 .
• Ланг, Серж (1985), Введение в линейную алгебру , Тексты для бакалавров по математике (2-е изд.), Springer, ISBN  9780387962054
• Ланг, Серж (1987), Линейная алгебра , Тексты для бакалавров по математике (3-е изд.), Springer, ISBN  9780387964126
• Ланг, Серж (2002). Алгебра Тексты для аспирантов по математике. Нью-Йорк, штат Нью-Йорк: Спрингер. ISBN  978-0-387-95385-4 .
• Леон, Стивен Дж. (2006), Линейная алгебра с приложениями (7-е изд.), Пирсон Прентис Холл
• Роте, Гюнтер (2001), «Алгоритмы без делений для определителя и пфаффиана: алгебраические и комбинаторные подходы» (PDF) , Вычислительная дискретная математика , Конспекты лекций по Comput. наук, том. 2122, Springer, стр. 119–135, номер документа : 10.1007/3-540-45506-X_9 , ISBN.  978-3-540-42775-9 , MR   1911585 , заархивировано из оригинала (PDF) 1 февраля 2007 г. , получено 4 июня 2020 г.
• Трефетен, Ллойд; Бау III, Дэвид (1997), Численная линейная алгебра (1-е изд.), Филадельфия: SIAM, ISBN  978-0-89871-361-9

Исторические справки

• Бурбаки, Николас (1994), Элементы истории математики , перевод Мелдрама, Джона, Спрингера, doi : 10.1007/978-3-642-61693-8 , ISBN  3-540-19376-6
• Каджори, Флориан (1993), История математических обозначений: включая Vol. I. Обозначения элементарной математики; Том. II. Обозначения в основном по высшей математике, Перепечатка оригиналов 1928 и 1929 годов , Дувр, ISBN  0-486-67766-4 , МР   3363427
• Безу, Этьен (1779), Общая теория алгебраических уравнений , Париж
• Кэли, Артур (1841), «Об одной теореме геометрии положения», Cambridge Mathematical Journal , 2 : 267–271.
• Крамер, Габриэль (1750), Введение в анализ алгебраических кривых линий , Женева: Frères Cramer & Cl Philibert, doi : 10.3931/e-rara-4048.
• Ивс, Ховард (1990), Введение в историю математики (6-е изд.), Saunders College Publishing, ISBN  0-03-029558-0 , МР   1104435
• Граттан-Гиннесс, И., изд. (2003), Сопутствующая энциклопедия истории и философии математических наук , том. 1, Издательство Университета Джонса Хопкинса , ISBN  9780801873966
• Якоби, Карл Густав Якоб (1841), «De Determinantibus Functionalibus» , Журнал чистой и прикладной математики , 1841 (22): 320–359, doi : 10.1515/crll.1841.22.319 , S2CID   123637858
• Лаплас, Пьер-Симон де (1772), «Исследование интегрального исчисления и мировой системы» , История Королевской академии наук (вторая часть), Париж: 267–376. {{citation}}: CS1 maint: несколько имен: список авторов ( ссылка )

Внешние ссылки

• Супруненко, Д.А. (2001) [1994], «Определитель» , Энциклопедия Математики , EMS Press
• Вайсштейн, Эрик В. «Определитель» . Математический мир .
• О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Матрицы и определители» , Архив истории математики MacTutor , Университет Сент-Эндрюс
• Интерактивная программа и руководство «Определитель»
• Линейная алгебра: определители. Архивировано 4 декабря 2008 г. в Wayback Machine. Вычислите определители матриц до 6-го порядка, используя выбранное вами расширение Лапласа.
• Калькулятор определителей Калькулятор определителей матриц до 8-го порядка.
• Матрицы и линейная алгебра на страницах самых ранних использований
• Определители в простой форме объяснены в 4-й главе в рамках курса линейной алгебры.