Разложение по сингулярным значениям

- Вверху: действие M , обозначенное его влиянием на единичный круг D и два канонических единичных вектора e 1 и e 2 .
- Слева: действие Ви. ⁎ , вращение на D , e 1 и e 2 .
- Внизу: действие Σ , масштабирование сингулярными значениями σ 1 по горизонтали и σ 2 по вертикали.
- Справа: действие U , еще одно вращение.
В линейной алгебре разложение по сингулярным значениям ( SVD ) представляет собой матрицы в с вращение факторизацию вещественной или комплексной последующим изменением масштаба и последующим вращением. Он обобщает собственное разложение квадратной нормальной матрицы с ортонормированным собственным базисом на любое матрица. Это связано с полярным разложением .
В частности, сингулярное разложение комплексная матрица является факторизацией формы где это комплексная унитарная матрица , это прямоугольная диагональная матрица с неотрицательными действительными числами на диагонали, это комплексная унитарная матрица и является транспонированием сопряженным . Такое разложение всегда существует для любой комплексной матрицы. Если реально, тогда и гарантированно могут быть вещественными ортогональными матрицами; в таких контекстах СВД часто обозначается
Диагональные записи из однозначно определяются и известны как значения сингулярные . Число ненулевых сингулярных значений рангу равно . Столбцы и столбцы называются левосингулярными векторами и правосингулярными векторами , соответственно. Они образуют два набора ортонормированных базисов. и и если они отсортированы так, что сингулярные значения со значением ноль все находятся в столбцах (или строках) с наибольшим номером, разложение по сингулярным значениям можно записать как
где это ранг
SVD не уникален, однако всегда можно выбрать такое разложение, при котором сингулярные значения находятся в порядке убывания. В этом случае, (но не и ) однозначно определяется
Термин иногда относится к компактной СВД , аналогичное разложение в котором квадратная диагональ размера где это ранг и имеет только ненулевые сингулярные значения. В этом варианте это полуунитарная матрица и это полуунитарная матрица такая, что
Математические приложения SVD включают вычисление псевдообратной матрицы, аппроксимацию и определение ранга, диапазона и нулевого пространства матрицы. SVD также чрезвычайно полезен во всех областях науки, техники и статистики , таких как обработка сигналов , аппроксимация данных методом наименьших квадратов и управление процессами .
интерпретации Интуитивные

Вращение, масштабирование координат и отражение [ править ]
В частном случае, когда это действительная квадратная матрица , матрицы и может быть выбран реальным матрицы тоже. В этом случае «унитарный» — это то же самое, что « ортогональный ». Затем, интерпретируя как унитарные матрицы, так и диагональную матрицу, обобщенную здесь как как линейное преобразование пространства матрицы и представляют собой вращения или отражение пространства, в то время как представляет масштабирование каждой координаты по фактору Таким образом, разложение SVD разрушает любое линейное преобразование в композицию трех геометрических преобразований : поворота или отражения ( ), с последующим покоординатным масштабированием ( ), за которым следует еще одно вращение или отражение ( ).
В частности, если имеет положительный определитель, то и можно выбрать оба вращения с отражениями или оба вращения без отражений. [ нужна ссылка ] Если определитель отрицательный, то ровно один из них будет иметь отражение. Если определитель равен нулю, каждый из них может быть независимо выбран для любого типа.
Если матрица веществен, но не квадратен, а именно с его можно интерпретировать как линейное преобразование из к Затем и могут быть выбраны в качестве вращений/отражений и соответственно; и помимо масштабирования первого координаты, также расширяет вектор нулями, т.е. удаляет конечные координаты, чтобы повернуть в
значения как полуоси эллипса эллипсоида или Сингулярные
Как показано на рисунке, сингулярные значения можно интерпретировать как величину полуосей эллипса в 2D. Эту концепцию можно обобщить на -мерное евклидово пространство с сингулярными значениями любого квадратная матрица рассматривается как величина полуоси -мерный эллипсоид . Аналогично, сингулярные значения любых матрицу можно рассматривать как величину полуоси -мерный эллипсоид в -мерное пространство, например, как эллипс в (наклоненной) 2D-плоскости в 3D-пространстве. Сингулярные значения кодируют величину полуоси, а сингулярные векторы кодируют направление. смотрите ниже Более подробную информацию .
Столбцы U и V являются ортонормированными . базисами
С и унитарны, столбцы каждого из них образуют набор ортонормированных векторов , которые можно рассматривать как базисные векторы . Матрица отображает базисный вектор к растянутому единичному вектору По определению унитарной матрицы то же самое верно и для ее сопряженных транспонирований. и за исключением того, что теряется геометрическая интерпретация сингулярных значений как растяжений. Короче говоря, столбцы и являются ортонормированными базисами . Когда – положительно-полуопределенная эрмитова матрица , и оба равны унитарной матрице, используемой для диагонализации Однако, когда не является положительно-полуопределенным и эрмитовым, но все же диагонализируемым , его собственное разложение и разложение по сингулярным значениям различны.
с четырьмя фундаментальными Связь подпространствами
- Первый столбцы являются основой столбцов пространства .
- Последний столбцы являются основой пространства нулевого .
- Первый столбцы являются основой пространства столбцов ( пространство строк в реальном случае).
- Последний столбцы являются основой нулевого пространства .
Геометрический смысл [ править ]
Потому что и унитарны, мы знаем, что столбцы из получить ортонормированный базис и столбцы из получить ортонормированный базис (относительно стандартных скалярных произведений на этих пространствах).
Линейное преобразование
имеет особенно простое описание относительно этих ортонормированных базисов: мы имеем
где это -й диагональный вход и для
Таким образом, геометрическое содержание теоремы SVD можно резюмировать следующим образом: для любого линейного отображения можно найти ортонормированные базисы и такой, что отображает -й базисный вектор неотрицательному кратному -й базисный вектор и отправляет оставшиеся базисные векторы в ноль. По отношению к этим базам карта поэтому представляется диагональной матрицей с неотрицательными действительными диагональными элементами.
Чтобы получить более наглядное представление о сингулярных значениях и факторизации SVD – по крайней мере, при работе с реальными векторными пространствами – рассмотрите сферу радиуса один дюйм Линейная карта отображает эту сферу на эллипсоид в Ненулевые сингулярные значения — это просто длины полуосей этого эллипсоида. Особенно когда и все сингулярные значения различны и ненулевые, SVD линейного отображения можно легко проанализировать как последовательность трех последовательных ходов: рассмотрим эллипсоид и конкретно его оси; затем рассмотрите направления в отправлено на эти оси. Эти направления оказываются взаимно ортогональными. Сначала примените изометрию отправляя эти направления к осям координат На втором ходу применим эндоморфизм диагонально по осям координат и растягивая или сжимая в каждом направлении, используя длины полуосей как коэффициенты растяжения. Состав затем отправляет единичную сферу на изометрический эллипсоид Чтобы определить третий и последний ход, примените изометрию к этому эллипсоиду, чтобы получить Как легко проверить, состав совпадает с
Пример [ править ]
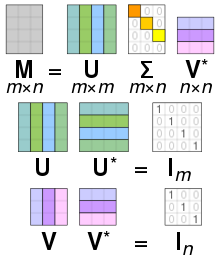
Рассмотрим матрица
Разложение этой матрицы по сингулярным значениям имеет вид
Матрица масштабирования равен нулю за пределами диагонали (серый курсив), а один диагональный элемент равен нулю (красный жирный шрифт, светло-синий жирный шрифт в темном режиме). Более того, поскольку матрицы и унитарны , , умножение на соответствующие им сопряженные транспонирования дает единичные матрицы как показано ниже. В этом случае, поскольку и имеют действительные значения, каждая из них является ортогональной матрицей .
Это конкретное разложение по сингулярным значениям не уникально. Выбор такой, что
также является допустимым разложением по сингулярным значениям.
СВД и спектральное разложение [ править ]
векторы и их связь SVD с Сингулярные значения, сингулярные
Неотрицательное действительное число является сингулярным значением для тогда и только тогда, когда существуют векторы единичной длины в и в такой, что
Векторы и называются левосингулярными и правосингулярными векторами для соответственно.
В любом разложении по сингулярным значениям
диагональные записи равны сингулярным значениям Первый столбцы и являются соответственно лево- и право-сингулярными векторами для соответствующих сингулярных значений. Следовательно, из приведенной выше теоремы следует, что:
- Ан матрица имеет не более отдельные единичные значения.
- Всегда можно найти унитарный базис для с подмножеством базисных векторов, охватывающим левосингулярные векторы каждого сингулярного значения
- Всегда можно найти унитарный базис для с подмножеством базисных векторов, охватывающим правосингулярные векторы каждого сингулярного значения
Сингулярное значение, для которого можно найти два левых (или правых) сингулярных вектора, линейно независимых, называется вырожденным . Если и являются двумя левосингулярными векторами, оба из которых соответствуют сингулярному значению σ, то любая нормализованная линейная комбинация этих двух векторов также является левосингулярным вектором, соответствующим сингулярному значению σ. Аналогичное утверждение справедливо и для правосингулярных векторов. Число независимых левых и правых сингулярных векторов совпадает, и эти сингулярные векторы находятся в одних и тех же столбцах таблицы. и соответствующие диагональным элементам все с одинаковой ценностью
В качестве исключения левый и правый сингулярные векторы сингулярного значения 0 содержат все единичные векторы в коядре и ядре соответственно который по теореме о ранге-нулях не может иметь одну и ту же размерность, если Даже если все сингулярные значения отличны от нуля, если то коядро нетривиально, и в этом случае дополнен ортогональные векторы из коядра. И наоборот, если затем дополняется ортогональные векторы из ядра. Однако если единственное значение существует, дополнительные столбцы или уже появляются как левые или право-сингулярные векторы.
Невырожденные сингулярные значения всегда имеют уникальные левые и правые сингулярные векторы, вплоть до умножения на единичный фазовый множитель. (для реального случая с точностью до знака). Следовательно, если все сингулярные значения квадратной матрицы невырождены и ненулевые, то его сингулярное разложение однозначно с точностью до умножения столбца на единичный фазовый коэффициент и одновременное умножение соответствующего столбца тем же единичным фазовым коэффициентом.В общем, SVD уникален с точностью до произвольных унитарных преобразований, равномерно применяемых к вектор-столбцам обоих и охватывающее подпространства каждого сингулярного значения, и с точностью до произвольных унитарных преобразований векторов и охватывающее ядро и коядро соответственно
Связь с разложением собственным значениям по
Разложение по сингулярным значениям является очень общим в том смысле, что его можно применять к любому матрица, тогда как разложение по собственным значениям может применяться только к квадратным диагонализуемым матрицам . Тем не менее, эти два разложения связаны.
Если есть СВД имеют место следующие два соотношения:
Правые части этих соотношений описывают разложения по собственным значениям левых частей. Следовательно:
- Столбцы (называемые правосингулярными векторами) являются собственными векторами
- Столбцы (называемые левосингулярными векторами) являются собственными векторами
- Ненулевые элементы (ненулевые сингулярные значения) являются квадратными корнями ненулевых собственных значений или
В частном случае Будучи нормальной матрицей и, следовательно, также квадратной, спектральная теорема гарантирует, что ее можно унитарно диагонализировать с использованием базиса собственных векторов и, таким образом, разложить как для некоторой унитарной матрицы и диагональная матрица со сложными элементами по диагонали. Когда является положительно полуопределенным , будут неотрицательными действительными числами, так что разложение также является разложением по сингулярным значениям. В противном случае его можно переделать в СВД, сдвинув фазу каждого либо к соответствующему или Естественная связь SVD с ненормальными матрицами осуществляется через теорему полярного разложения : где является положительно полуопределенным и нормальным, а является унитарным.
Таким образом, за исключением положительных полуопределенных матриц, разложение по собственным значениям и SVD будучи связанными, они различаются: разложение по собственным значениям где не обязательно унитарен и не обязательно положительно полуопределенный, а SVD где является диагональным и положительно полуопределенным, а и представляют собой унитарные матрицы, которые не обязательно связаны друг с другом, кроме как через матрицу Хотя только недефектные квадратные матрицы, любые разложение по собственным значениям имеют матрица имеет СВД.
Применение СВД [ править ]
Псевдообратный [ править ]
Разложение по сингулярным значениям можно использовать для вычисления псевдообратной матрицы. Псевдообратная матрица с разложением по сингулярным значениям является,
где является псевдообратным , которая формируется путем замены каждой ненулевой диагональной записи на обратную и транспонирования полученной матрицы. Псевдообратное - это один из способов решения линейных задач наименьших квадратов .
Решение однородных линейных уравнений [ править ]
Совокупность однородных линейных уравнений можно записать в виде для матрицы и вектор Типичная ситуация заключается в том, что известно и ненулевое значение необходимо определить, который удовлетворяет уравнению. Такой принадлежит пустое пространство и иногда называется (правым) нулевым вектором Вектор может быть охарактеризован как правосингулярный вектор, соответствующий сингулярному значению это ноль. Это наблюдение означает, что если является квадратной матрицей и не имеет исчезающего сингулярного значения, уравнение не имеет ненулевых значений. как решение. Это также означает, что если существует несколько исчезающих сингулярных значений, любая линейная комбинация соответствующих правосингулярных векторов является допустимым решением. Аналогично определению (правого) нулевого вектора, ненулевой удовлетворяющий с обозначающий сопряженный транспонирование называется левым нулевым вектором
Полная минимизация методом наименьших квадратов [ править ]
Задача полного наименьших квадратов ищет вектор что минимизирует 2-норму вектора под ограничением Решением оказывается правосингулярный вектор соответствующий наименьшему единственному значению.
Диапазон, пустое пространство и ранг [ править ]
Другое применение SVD заключается в том, что он обеспечивает явное представление диапазона и нулевого пространства матрицы. Правосингулярные векторы, соответствующие исчезающим сингулярным значениям охватывать нулевое пространство и левосингулярные векторы, соответствующие ненулевым сингулярным значениям охватывать диапазон Например, в приведенном выше примере пустое пространство охватывает последнюю строку и диапазон охватывает первые три столбца
следствие, ранг Как равно количеству ненулевых сингулярных значений, которое совпадает с количеством ненулевых диагональных элементов в . В числовой линейной алгебре сингулярные значения могут использоваться для определения эффективного ранга матрицы, поскольку ошибка округления может привести к небольшим, но ненулевым сингулярным значениям в матрице с недостаточным рангом. Предполагается, что сингулярные значения за пределами значительного разрыва численно эквивалентны нулю.
низкого Матричная аппроксимация ранга
В некоторых практических приложениях необходимо решить задачу аппроксимации матрицы. с другой матрицей , который называется усеченным , имеет определенный ранг . В случае, когда аппроксимация основана на минимизации нормы Фробениуса разности между и при условии, что оказывается, что решение даёт СВД а именно
где та же матрица, что и за исключением того, что он содержит только наибольшие сингулярные значения (остальные сингулярные значения заменяются нулем). Это известно как теорема Эккарта-Янга , поскольку она была доказана этими двумя авторами в 1936 году (хотя позже выяснилось, что она была известна более ранним авторам; см. Stewart 1993 ).
Разделяемые модели [ править ]
SVD можно рассматривать как разложение матрицы на взвешенную упорядоченную сумму разделимых матриц. Под сепарабельностью мы подразумеваем, что матрица можно записать как внешнее произведение двух векторов или, в координатах, В частности, матрица можно разложить как,
Здесь и являются -ые столбцы соответствующих матриц SVD, являются упорядоченными сингулярными значениями, и каждое является разделимым. SVD можно использовать для поиска разложения фильтра обработки изображений на отдельные горизонтальные и вертикальные фильтры. Обратите внимание, что число ненулевых это в точности ранг матрицы. [ нужна ссылка ] Разделимые модели часто возникают в биологических системах, и факторизация SVD полезна для анализа таких систем. Например, рецептивные поля простых клеток зрительной области V1 могут быть хорошо описаны. [1] фильтром Габора в пространственной области, умноженным на функцию модуляции во временной области. Таким образом, учитывая линейный фильтр, оцененный, например, с помощью обратной корреляции , можно перегруппировать два пространственных измерения в одно измерение, получив таким образом двумерный фильтр (пространство, время), который можно разложить с помощью SVD. Первый столбец в факторизации SVD тогда является Габором, а первый столбец представляет временную модуляцию (или наоборот). Затем можно определить индекс разделимости
которая представляет собой долю мощности в матрице M, которая учитывается первой сепарабельной матрицей в разложении. [2]
матрица ортогональная Ближайшая
Возможно использование СВД с квадратной матрицей определить ортогональную матрицу ближайший к Близость соответствия измеряется нормой Фробениуса . Решение – это продукт [3] Это интуитивно имеет смысл, поскольку ортогональная матрица будет иметь разложение где – единичная матрица, так что если тогда продукт сводится к замене сингулярных значений единицами. Эквивалентно, решением является унитарная матрица полярного разложения в любом порядке растяжения и вращения, как описано выше.
Похожая проблема, имеющая интересные применения в анализе формы , — это ортогональная задача Прокруста , которая состоит в нахождении ортогональной матрицы. который наиболее точно отображает к Конкретно,
где обозначает норму Фробениуса.
Эта проблема эквивалентна поиску ближайшей ортогональной матрицы к заданной матрице. .
Алгоритм Кабша [ править ]
Алгоритм Кабша (в других областях называемый проблемой Вахбы ) использует SVD для вычисления оптимального вращения (относительно минимизации по методу наименьших квадратов), которое выравнивает набор точек с соответствующим набором точек. Он используется, среди прочего, для сравнения структур молекул.
Обработка сигналов [ править ]
SVD и псевдоинверсия успешно применяются для обработки сигналов . [4] обработка изображений [5] и большие данные (например, при обработке геномных сигналов). [6] [7] [8] [9]
Другие примеры [ править ]
SVD также широко применяется для изучения линейных обратных задач и полезен при анализе методов регуляризации, таких как метод Тихонова . Он широко используется в статистике, где он связан с анализом главных компонент и анализом соответствий , а также в обработке сигналов и распознавании образов . Он также используется в модальном анализе только для выходных данных , где немасштабированные формы мод могут быть определены по сингулярным векторам. Еще одно использование — это скрытая семантическая индексация при обработке текста на естественном языке.
В общих численных вычислениях с участием линейных или линеаризованных систем существует универсальная константа, характеризующая регулярность или сингулярность проблемы, которая представляет собой «число состояния» системы. . Он часто контролирует частоту ошибок или скорость сходимости данной вычислительной схемы в таких системах. [10] [11]
SVD также играет решающую роль в области квантовой информации в форме, часто называемой разложением Шмидта . Благодаря ему состояния двух квантовых систем естественным образом разлагаются, обеспечивая необходимое и достаточное условие для их запутанности : если ранг матрица больше единицы.
Одним из применений SVD к довольно большим матрицам является численный прогноз погоды , где методы Ланцоша используются для оценки наиболее линейно быстро растущих немногих возмущений центрального численного прогноза погоды в течение заданного начального периода вперед; т. е. сингулярные векторы, соответствующие наибольшим сингулярным значениям линеаризованного пропагатора глобальной погоды за этот интервал времени. Выходными сингулярными векторами в этом случае являются целые погодные системы. Эти возмущения затем прогоняются через полную нелинейную модель для создания ансамблевого прогноза , что дает возможность справиться с некоторой неопределенностью, которую следует учитывать в отношении текущего центрального прогноза.
SVD также применяется для моделирования уменьшенного порядка. Целью моделирования пониженного порядка является уменьшение количества степеней свободы в сложной системе, которую необходимо моделировать. SVD сочетался с радиальными базисными функциями для интерполяции решений трехмерных задач нестационарного течения. [12]
Интересно, что SVD использовался для улучшения моделирования гравитационных волн с помощью наземного гравитационно-волнового интерферометра aLIGO. [13] SVD может помочь повысить точность и скорость генерации сигналов для поддержки поиска гравитационных волн и обновления двух различных моделей сигналов.
Разложение по сингулярным значениям используется в рекомендательных системах для прогнозирования оценок людей. [14] С целью расчета СВД на кластерах товарных машин разработаны распределенные алгоритмы. [15]
SVD низкого ранга применялся для обнаружения горячих точек на основе пространственно-временных данных с применением для обнаружения вспышек заболеваний . [16] Комбинация SVD и SVD более высокого порядка также применялась для обнаружения событий в реальном времени из сложных потоков данных (многомерные данные с пространственными и временными измерениями) при эпиднадзоре за заболеваниями . [17]
В астродинамике СВД и ее варианты используются как вариант для определения подходящих направлений маневра при проектировании траектории полета. [18] и поддержание орбитальной станции . [19]
Доказательство существования [ править ]
собственное значение матрицы характеризуется алгебраическим соотношением Когда является эрмитовым , также доступна вариационная характеристика. Позволять быть настоящим симметричная матрица . Определять
По теореме о крайних значениях эта непрерывная функция достигает максимума в некоторой точке. при ограничении единичной сферой По о множителях Лагранжа теореме обязательно удовлетворяет
для некоторого действительного числа Символ набла, , – оператор del (дифференцирование по ). Используя симметрию мы получаем
Поэтому так — собственный вектор единичной длины Для каждого собственного вектора единичной длины из его собственное значение так является наибольшим собственным значением Тот же расчет выполнен для ортогонального дополнения дает следующее по величине собственное значение и так далее. Сложный эрмитовский случай аналогичен; там является вещественной функцией реальные переменные.
Сингулярные значения схожи тем, что их можно описать алгебраически или с помощью вариационных принципов. Хотя, в отличие от случая собственных значений, эрмитичность или симметрия больше не требуется.
В этом разделе приводятся эти два аргумента в пользу существования разложения по сингулярным значениям.
На основе спектральной теоремы [ править ]
Позволять быть сложная матрица. С является положительно полуопределенным и эрмитовым, по спектральной теореме существует унитарная матрица такой, что
где диагональна и положительно определена, имеет размерность , с количество ненулевых собственных значений (что можно показать для проверки ). Обратите внимание, что здесь по определению является матрицей, у которой -й столбец - это -й собственный вектор , соответствующий собственному значению . Более того, -й столбец , для , является собственным вектором с собственным значением . Это можно выразить, написав как , где столбцы и поэтому содержат собственные векторы соответствующие ненулевым и нулевым собственным значениям соответственно. Используя это переписывание , уравнение принимает вид:
Это подразумевает, что
Более того, из второго уравнения следует . [20] Наконец, унитарность переводится, с точки зрения и , в следующие условия:
где индексы у единичных матриц используются для обозначения того, что они имеют разные размерности.
Давайте теперь определим
Затем,
с Это также можно рассматривать как непосредственное следствие того факта, что . Это эквивалентно наблюдению, что если представляет собой набор собственных векторов соответствующие ненулевым собственным значениям , затем представляет собой набор ортогональных векторов, а представляет собой (вообще не полный) набор ортонормированных векторов. Это соответствует использованному выше матричному формализму, обозначающему матрица, столбцы которой , с матрица, столбцы которой являются собственными векторами с исчезающим собственным значением, и матрица, столбцы которой являются векторами .
Мы видим, что это почти желаемый результат, за исключением того, что и в общем случае не унитарны, поскольку могут быть не квадратными. Однако мы знаем, что количество строк не меньше числа столбцов, так как размеры не больше, чем и . Кроме того, поскольку
столбцы в ортонормированы и могут быть расширены до ортонормированного базиса. Это означает, что мы можем выбирать такой, что является унитарным.
Для у нас уже есть сделать его единым. Теперь определите
где дополнительные нулевые строки добавляются или удаляются , чтобы количество нулевых строк равнялось количеству столбцов отсюда и габаритные размеры равный . Затем
какой желаемый результат:
Обратите внимание, что аргумент может начаться с диагонализации скорее, чем (Это прямо показывает, что и имеют одинаковые ненулевые собственные значения).
На основе вариационной характеристики [ править ]
Сингулярные значения также можно охарактеризовать как максимумы рассматривать как функцию и над конкретными подпространствами. Сингулярные векторы — это значения и где эти максимумы достигаются.
Позволять обозначают матрица с реальными элементами. Позволять быть единицей -сфера в и определить
Рассмотрим функцию ограничено Поскольку оба и являются компактными множествами, их произведение также компактно. Кроме того, поскольку непрерывен, он достигает максимального значения хотя бы для одной пары векторов в и в Это наибольшее значение обозначается и соответствующие векторы обозначаются и С является наибольшим значением оно должно быть неотрицательным. Если бы оно было отрицательным, то изменение знака либо или сделало бы его положительным и, следовательно, большим.
Заявление. и являются левыми и право-сингулярными векторами с соответствующим сингулярным значением
Доказательство. Как и в случае с собственными значениями, по предположению, два вектора удовлетворяют уравнению множителя Лагранжа:
После некоторой алгебры это становится
Умножив первое уравнение слева на и второе уравнение слева на и принимая во внимание дает
Подставив это в пару приведенных выше уравнений, мы имеем
Это доказывает утверждение.
Больше сингулярных векторов и сингулярных значений можно найти, максимизируя сверхнормализованный и которые ортогональны и соответственно.
Переход от действительного к комплексному аналогичен случаю собственных значений.
Расчет СВД [ править ]
Односторонний алгоритм Якоби [ править ]
Односторонний алгоритм Якоби — это итерационный алгоритм, [21] где матрица итеративно преобразуется в матрицу с ортогональными столбцами. Элементарная итерация задается как вращение Якоби ,
где угол матрицы вращения Якоби выбирается таким, чтобы после поворота столбцы с номерами и станут ортогональными. Индексы циклически перемещаются, , где это количество столбцов.
После сходимости алгоритма разложение по сингулярным значениям восстанавливается следующим образом: матрица – накопление матриц вращения Якоби, матрица определяется путем нормализации столбцов преобразованной матрицы , а сингулярные значения заданы как нормы столбцов преобразованной матрицы .
Двусторонний алгоритм Якоби [ править ]
Двусторонний алгоритм Якоби SVD — обобщение алгоритма собственных значений Якоби — представляет собой итерационный алгоритм, в котором квадратная матрица итеративно преобразуется в диагональную матрицу. Если матрица не квадратная, сначала выполняется QR-разложение , а затем алгоритм применяется к матрица. Элементарная итерация обнуляет пару недиагональных элементов, сначала применяя вращение Гивенса для симметризации пары элементов, а затем применяя преобразование Якоби для их обнуления:
где - матрица вращения Гивенса с углом, выбранным таким образом, что данная пара недиагональных элементов становится равной после вращения, и где — матрица преобразования Якоби, которая обнуляет эти недиагональные элементы. Итерации происходят точно так же, как в алгоритме собственных значений Якоби: циклическим проходом по всем недиагональным элементам.
После сходимости алгоритма результирующая диагональная матрица содержит сингулярные значения.Матрицы и накапливаются следующим образом: , .
Численный подход [ править ]
Разложение по сингулярным значениям можно вычислить, используя следующие наблюдения:
- Левосингулярные векторы набор ортонормированных собственных векторов представляют собой .
- Правосингулярные векторы представляют собой набор ортонормированных собственных векторов .
- Ненулевые сингулярные значения (находится на диагональных записях ) являются квадратными корнями из ненулевых собственных значений обоих и .
СВД матрицы обычно вычисляется с помощью двухэтапной процедуры. На первом этапе матрица сводится к двудиагональной матрице . Это требует порядка операции с плавающей запятой (флоп), предполагая, что Второй шаг — вычислить SVD двудиагональной матрицы. Этот шаг можно выполнить только итеративным методом (как в случае с алгоритмами собственных значений ). Однако на практике достаточно вычислить СВД с определенной точностью, как машинный эпсилон . Если эту точность считать постоянной, то второй шаг принимает итераций, стоимость каждой проваливается. Таким образом, первый шаг обходится дороже, а общая стоимость составляет проваливается ( Trefethen & Bau III 1997 , лекция 31).
Первый шаг можно сделать, используя отражения Хаусхолдера , заплатив проваливается, если предположить, что нужны только сингулярные значения, а не сингулярные векторы. Если намного больше, чем то выгодно сначала уменьшить матрицу к треугольной матрице с QR-разложением , а затем использовать отражения Хаусхолдера для дальнейшего приведения матрицы к двудиагональной форме; общая стоимость составляет проваливается ( Trefethen & Bau III 1997 , лекция 31).
Второй шаг можно выполнить с помощью варианта QR-алгоритма для вычисления собственных значений, который впервые был описан Голубом и Каханом (1965) . Подпрограмма LAPACK DBDSQR [22] реализует этот итерационный метод с некоторыми модификациями, чтобы охватить случай, когда сингулярные значения очень малы ( Demmel & Kahan 1990 ). Вместе с первым шагом с использованием отражений Хаусхолдера и, если необходимо, QR-разложения, это формирует DGESVD. [23] подпрограмма для вычисления разложения по сингулярным значениям.
Тот же алгоритм реализован в Научной библиотеке GNU (GSL). GSL также предлагает альтернативный метод, который использует одностороннюю ортогонализацию Якоби на шаге 2 ( GSL Team 2007 ). Этот метод вычисляет SVD двудиагональной матрицы, решая последовательность Проблемы SVD, аналогичные тому, как алгоритм собственных значений Якоби решает последовательность методы собственных значений ( Голуб и Ван Лоан 1996 , §8.6.3). Еще один метод для шага 2 использует идею алгоритмов собственных значений «разделяй и властвуй» ( Trefthen & Bau III 1997 , лекция 31).
Существует альтернативный способ, который явно не использует разложение по собственным значениям. [24] Обычно сингулярная задача матрицы преобразуется в эквивалентную симметричную задачу собственных значений, например или
Подходы, использующие разложение по собственным значениям, основаны на алгоритме QR , который хорошо разработан, чтобы быть стабильным и быстрым. Обратите внимание, что сингулярные значения являются действительными, а право- и левосингулярные векторы не требуются для формирования преобразований подобия. Можно итеративно чередовать QR-разложение и LQ-разложение, чтобы найти действительные диагональные эрмитовы матрицы . QR -разложение дает и LQ- разложение дает Таким образом, на каждой итерации мы имеем обновлять и повторите ортогонализации. В конце концов, [ нужны разъяснения ] эта итерация между QR-разложением и LQ-разложением дает левые и правые унитарные сингулярные матрицы. Этот подход невозможно ускорить, как это можно сделать с помощью алгоритма QR с помощью спектральных сдвигов или дефляции. Это связано с тем, что метод сдвига нелегко определить без использования преобразований подобия. Однако этот итеративный подход очень прост в реализации, поэтому он является хорошим выбором, когда скорость не имеет значения. Этот метод также дает представление о том, как чисто ортогональные/унитарные преобразования могут получить SVD.
результат 2× Аналитический 2 СВД
Сингулярные значения a матрицу можно найти аналитически. Пусть матрица будет
где являются комплексными числами, которые параметризуют матрицу, - единичная матрица, и обозначим матрицы Паули . Тогда два его сингулярных значения определяются выражением
Уменьшенные СВД [ править ]

В приложениях довольно редко требуется полное SVD, включая полное унитарное разложение нулевого пространства матрицы. Вместо этого часто бывает достаточно (а также быстрее и экономичнее с точки зрения хранения) вычислить уменьшенную версию SVD. Для матрица ранга :
Тонкая СВД [ править ]
Тонкая или экономичная SVD-матрица дается [25]
где матрицы и содержать только первый столбцы и и содержит только первый сингулярные значения из Матрица таким образом является диагональ, -и является
Тонкий SVD использует значительно меньше места и времени вычислений, если Первым этапом его расчета обычно будет -разложение QR что в этом случае может значительно ускорить расчет.
Компактная СВД [ править ]
Компактная СВД матрицы дается
Только векторы-столбцы и векторы-строки соответствующие ненулевым сингулярным значениям рассчитываются. Остальные векторы и не рассчитываются. Это быстрее и экономичнее тонкой СВД, если Матрица таким образом является диагональ, -и является
Усеченная СВД [ править ]
Во многих приложениях число ненулевых сингулярных значений велико, что делает непрактичным вычисление даже Compact SVD. В таких случаях наименьшие сингулярные значения, возможно, придется усечь, чтобы вычислить только ненулевые сингулярные значения. Усеченная СВД больше не является точным разложением исходной матрицы а скорее обеспечивает оптимальную аппроксимацию матрицы низкого ранга по любой матрице фиксированного ранга
где матрица является является диагональ, -и является Только векторы-столбцы и векторы-строки соответствующий наибольшие сингулярные значения рассчитываются. Это может быть намного быстрее и экономичнее, чем компактная СВД, если но требует совершенно другого набора численных решателей.
В приложениях, требующих приближения к Мура – Пенроуза обратной матрице наименьшие сингулярные значения представляют интерес, которые сложнее вычислить по сравнению с самыми крупными.
Усеченный SVD используется при скрытой семантической индексации . [26]
Нормы [ править ]
Нормы Кай Фана [ править ]
Сумма наибольшие сингулярные значения является матричной нормой , Кай Фань -норма [27]
Первая из норм Кай Фана, 1-норма Кай Фана, совпадает с операторной нормой как линейный оператор относительно евклидовых норм и Другими словами, 1-норма Кай Фана — это операторная норма, индуцированная стандартом Евклидов внутренний продукт. По этой причине его еще называют оператором 2-нормы. Легко проверить связь между 1-нормой Кай Фана и сингулярными значениями. В общем случае это верно для ограниченного оператора на (возможно, бесконечномерных) гильбертовых пространствах
Но в матричном случае это нормальная матрица , поэтому является наибольшим собственным значением т.е. наибольшее единственное значение
Последняя из норм Кай Фана, сумма всех сингулярных значений, представляет собой норму следа (также известную как «ядерная норма»), определяемую формулой (собственные значения являются квадратами сингулярных значений).
Норма Гильберта – Шмидта [ править ]
Сингулярные значения связаны с другой нормой в пространстве операторов. Рассмотрим скалярное произведение Гильберта–Шмидта на матрицы, определяемые
Таким образом, индуцированная норма равна
Поскольку след инвариантен относительно унитарной эквивалентности, это показывает
где являются сингулярными значениями Это называется нормой Фробениуса , 2-нормой Шаттена или нормой Гильберта–Шмидта . Прямой расчет показывает, что норма Фробениуса совпадает с:
Кроме того, норма Фробениуса и норма следа (ядерная норма) являются частными случаями нормы Шаттена .
Вариации и обобщения [ править ]
Масштабно-инвариантный СВД [ править ]
Сингулярные значения матрицы определены однозначно и инвариантны относительно левых и/или правых унитарных преобразований Другими словами, сингулярные значения для унитарных матриц и равны сингулярным значениям Это важное свойство для приложений, в которых необходимо сохранить евклидовы расстояния и инвариантность относительно вращений.
Масштабно-инвариантный SVD или SI-SVD, [28] аналогичен обычному SVD, за исключением того, что его однозначно определенные сингулярные значения инвариантны относительно диагональных преобразований Другими словами, сингулярные значения для обратимых диагональных матриц и равны сингулярным значениям Это важное свойство для приложений, для которых необходима инвариантность к выбору единиц измерения переменных (например, метрических или имперских единиц).
операторы в Ограниченные пространствах гильбертовых
Факторизация можно расширить до ограниченного оператора в сепарабельном гильбертовом пространстве А именно, для любого ограниченного оператора существует частичная изометрия унитарный пространство меры и неотрицательное измеримое такой, что
где это умножение на на
Это можно показать, подражая линейному алгебраическому аргументу для матричного случая, приведенного выше. уникальный положительный квадратный корень из как задано функциональным исчислением Бореля для самосопряженных операторов . Причина, почему не обязательно должен быть унитарным, заключается в том, что, в отличие от конечномерного случая, при наличии изометрии с нетривиальным ядром, подходящий не может быть найдено такое, что
является унитарным оператором.
Что касается матриц, то факторизация сингулярных значений эквивалентна полярному разложению операторов: мы можем просто написать
и заметьте, что все еще является частичной изометрией, в то время как является положительным.
Сингулярные значения и компактные операторы [ править ]
Понятие сингулярных значений и лево/правосингулярных векторов можно расширить до компактного оператора в гильбертовом пространстве, поскольку они имеют дискретный спектр. Если компактен, каждое ненулевое в его спектре является собственным значением. Более того, компактный самосопряженный оператор можно диагонализовать по собственным векторам. Если компактен, поэтому . Применяя результат диагонализации, унитарный образ его положительного квадратного корня имеет набор ортонормированных собственных векторов соответствующие строго положительным собственным значениям . Для любого в
где ряд сходится в топологии нормы на Обратите внимание, как это похоже на выражение из конечномерного случая. называются сингулярными значениями (соответственно ) можно считать левосингулярными (соответственно правосингулярными) векторами
Компактные операторы в гильбертовом пространстве являются замыканием операторов конечного ранга в равномерной операторной топологии. Приведенное выше выражение ряда дает явное такое представление. Непосредственным следствием этого является:
- Теорема. компактен тогда и только тогда, когда компактен.
История [ править ]
Разложение по сингулярным значениям первоначально было разработано дифференциальными геометрами , которые хотели определить, можно ли сделать действительную билинейную форму равной другой путем независимых ортогональных преобразований двух пространств, на которые она действует. Эухенио Бельтрами и Камилла Джордан независимо открыли в 1873 и 1874 годах соответственно, что сингулярные значения билинейных форм, представленные в виде матрицы, образуют полный набор инвариантов для билинейных форм при ортогональных заменах. Джеймс Джозеф Сильвестр также пришел к разложению по сингулярным значениям для вещественных квадратных матриц в 1889 году, по-видимому, независимо от Бельтрами и Джордана. Сильвестр назвал сингулярные значения каноническими множителями матрицы. Четвертым математиком, независимо открывшим разложение по сингулярным числам, является Отонн в 1915 году, который пришел к нему с помощью полярного разложения . Первое доказательство разложения по сингулярным значениям для прямоугольных и комплексных матриц было сделано Карлом Эккартом и Гейлом Дж. Янгом в 1936 году; [29] они видели в этом обобщение преобразования главной оси для эрмитовых матриц .
В 1907 году Эрхард Шмидт определил аналог сингулярных значений для интегральных операторов (которые компактны при некоторых слабых технических предположениях); похоже, он не знал о параллельных работах по сингулярным значениям конечных матриц. Эта теория получила дальнейшее развитие Эмиля Пикара в 1910 году, который первым назвал числа сингулярные значения (или по-французски Valeurs Singulaires ).
Практические методы расчета СВД восходят к Когбетлянцу в 1954–1955 годах и Хестенесу в 1958 году. [30] очень похоже на алгоритм собственных значений Якоби , который использует вращения плоскости или вращения Гивенса . Однако они были заменены методом Джина Голуба и Уильяма Кахана, опубликованным в 1965 году. [31] который использует преобразования или отражения Хаусхолдера . В 1970 году Голуб и Кристиан Рейнш [32] опубликовал вариант алгоритма Голуба/Кахана, который до сих пор является наиболее используемым.
См. также [ править ]
- Каноническая корреляция
- Каноническая форма
- Анализ соответствия (СА)
- Проклятие размерности
- Цифровая обработка сигналов
- Уменьшение размерности
- Собственное разложение матрицы
- Эмпирические ортогональные функции (ЭОФ)
- Фурье-анализ
- Обобщенное разложение по сингулярным значениям
- Неравенства относительно сингулярных значений
- К-СВД
- Скрытый семантический анализ
- Скрытая семантическая индексация
- Линейный метод наименьших квадратов
- Список преобразований, связанных с Фурье
- Хэширование с учетом местоположения
- Низкоранговое приближение
- Разложение матрицы
- Многолинейный анализ главных компонент (MPCA)
- Поиск ближайшего соседа
- Нелинейный итеративный частичный метод наименьших квадратов
- Полярное разложение
- Анализ главных компонентов (PCA)
- Разложение Шмидта
- Смит, нормальная форма
- Единственное значение
- Временной ряд
- Двумерное сингулярное разложение (2DSVD)
- неравенство следов фон Неймана
- Вейвлет-сжатие
Примечания [ править ]
- ^ ДеАнджелис, GC; Одзава, И.; Фриман, Р.Д. (октябрь 1995 г.). «Динамика рецептивных полей в центральных зрительных путях». Тенденции нейробиологии . 18 (10): 451–8. дои : 10.1016/0166-2236(95)94496-Р . ПМИД 8545912 . S2CID 12827601 .
- ^ Депирё, Д.А.; Саймон, Джей Зи; Кляйн, диджей; Шамма, SA (март 2001 г.). «Характеристика спектрально-временного поля реакции с динамическими пульсациями в первичной слуховой коре хорька». Дж. Нейрофизиология . 85 (3): 1220–34. дои : 10.1152/jn.2001.85.3.1220 . ПМИД 11247991 .
- ^ Разложение по сингулярным значениям при симметричной (Lowdin) ортогонализации и сжатии данных
- ^ Сахидулла, штат Мэриленд; Киннунен, Томи (март 2016 г.). «Функции локальной спектральной изменчивости для проверки динамиков» . Цифровая обработка сигналов . 50 : 1–11. дои : 10.1016/j.dsp.2015.10.011 .
- ^ Мадемлис, Иоаннис; Тефас, Анастасиос; Питас, Иоаннис (2018). «Регуляризованная значимость видеокадров на основе SVD для обобщения видео неконтролируемых действий». Международная конференция IEEE по акустике, речи и обработке сигналов (ICASSP) 2018 г. IEEE. стр. 2691–2695. дои : 10.1109/ICASSP.2018.8462274 . ISBN 978-1-5386-4658-8 . S2CID 52286352 . Проверено 19 января 2023 г.
- ^ О. Альтер, П.О. Браун и Д. Ботштейн (сентябрь 2000 г.). «Разложение по сингулярным значениям для обработки и моделирования данных полногеномной экспрессии» . ПНАС . 97 (18): 10101–10106. Бибкод : 2000PNAS...9710101A . дои : 10.1073/pnas.97.18.10101 . ПМК 27718 . ПМИД 10963673 .
- ^ О. Альтер; Голубь Г.Х. (ноябрь 2004 г.). «Интегративный анализ данных в масштабе генома с использованием псевдообратной проекции предсказывает новую корреляцию между репликацией ДНК и транскрипцией РНК» . ПНАС . 101 (47): 16577–16582. Бибкод : 2004PNAS..10116577A . дои : 10.1073/pnas.0406767101 . ПМК 534520 . ПМИД 15545604 .
- ^ О. Альтер; Голубь Г.Х. (август 2006 г.). «Разложение по сингулярным значениям распределения длин мРНК в масштабе генома выявляет асимметрию в расширении полосы гель-электрофореза РНК» . ПНАС . 103 (32): 11828–11833. Бибкод : 2006PNAS..10311828A . дои : 10.1073/pnas.0604756103 . ПМЦ 1524674 . ПМИД 16877539 .
- ^ Бертаньолли, Нью-Мексико; Дрейк, Дж.А.; Теннессен, Дж. М.; Альтер, О. (ноябрь 2013 г.). «SVD идентифицирует функции распределения длины транскрипта на основе данных микрочипов ДНК и выявляет эволюционные силы, глобально влияющие на метаболизм ГБМ» . ПЛОС ОДИН . 8 (11): е78913. Бибкод : 2013PLoSO...878913B . дои : 10.1371/journal.pone.0078913 . ПМЦ 3839928 . ПМИД 24282503 . Выделять .
- ^ Эдельман, Алан (1992). «О распределении масштабированного числа состояния» (PDF) . Математика. Комп . 58 (197): 185–190. Бибкод : 1992MaCom..58..185E . дои : 10.1090/S0025-5718-1992-1106966-2 .
- ^ Шен, Цзяньхун (Джеки) (2001). «Об сингулярных значениях гауссовских случайных матриц» . Линейный Алг. Приложение . 326 (1–3): 1–14. дои : 10.1016/S0024-3795(00)00322-0 .
- ^ Уолтон, С.; Хасан, О.; Морган, К. (2013). «Моделирование пониженного порядка нестационарного потока жидкости с использованием правильного ортогонального разложения и радиальных базисных функций» . Прикладное математическое моделирование . 37 (20–21): 8930–8945. дои : 10.1016/j.apm.2013.04.025 .
- ^ Сетьявати, Ю.; Оме, Ф.; Хан, С. (2019). «Улучшение модели гравитационных сигналов посредством динамической калибровки». Физический обзор D . 99 (2): 024010. arXiv : 1810.07060 . Бибкод : 2019PhRvD..99b4010S . дои : 10.1103/PhysRevD.99.024010 . S2CID 118935941 .
- ^ Сарвар, Бадрул; Карипис, Георгий; Констан, Джозеф А. и Ридл, Джон Т. (2000). «Применение уменьшения размерности в рекомендательной системе – практический пример» (PDF) . Университет Миннесоты .
{{cite journal}}: Для цитирования журнала требуется|journal=( помощь ) - ^ Босах Заде, Реза; Карлссон, Гуннар (2013). «Квадрат матрицы, не зависящий от измерения, с использованием MapReduce» (PDF) . arXiv : 1304.1467 . Бибкод : 2013arXiv1304.1467B .
{{cite journal}}: Для цитирования журнала требуется|journal=( помощь ) - ^ Хади Фанаи Торк; Жоау Гама (сентябрь 2014 г.). «Метод собственного пространства для обнаружения пространственно-временных горячих точек». Экспертные системы . 32 (3): 454–464. arXiv : 1406.3506 . Бибкод : 2014arXiv1406.3506F . дои : 10.1111/exsy.12088 . S2CID 15476557 .
- ^ Хади Фанаи Торк; Жоау Гама (май 2015 г.). «EigenEvent: алгоритм обнаружения событий из сложных потоков данных при синдромном наблюдении». Интеллектуальный анализ данных . 19 (3): 597–616. arXiv : 1406.3496 . дои : 10.3233/IDA-150734 . S2CID 17966555 .
- ^ Муралидхаран, Вивек; Хауэлл, Кэтлин (2023). «Направления растяжения в окололунном пространстве: Заявки на вылеты и проектирование трансферов». Астродинамика . 7 (2): 153–178. Бибкод : 2023AsDyn...7..153M . дои : 10.1007/s42064-022-0147-z . S2CID 252637213 .
- ^ Муралидхаран, Вивек; Хауэлл, Кэтлин (2022). «Использование направлений растяжения для поддержания местоположения на галоорбитах Земля-Луна». Достижения в космических исследованиях . 69 (1): 620–646. Бибкод : 2022AdSpR..69..620M . дои : 10.1016/j.asr.2021.10.028 . S2CID 239490016 .
- ^ Чтобы увидеть это, нам просто нужно заметить, что , и помните это .
- ^ Райк, PPM де (1989). «Односторонний алгоритм Якоби для вычисления разложения по сингулярным значениям на векторном компьютере». СИАМ J. Sci. Стат. Вычислить . 10 : 359.
- ^ Netlib.org
- ^ Netlib.org
- ^ mathworks.co.kr/matlabcentral/fileexchange/12674-simple-svd
- ^ Деммель, Джеймс (2000). «Разложения» . Шаблоны для решения алгебраических задач на собственные значения . Бай, Чжаоцзюнь; Деммель, Джеймс; Донгарра, Джек Дж.; Руэ, Аксель; ван дер Ворст, Хенк А. Общество промышленной и прикладной математики. дои : 10.1137/1.9780898719581 . ISBN 978-0-89871-471-5 .
- ^ Чикко, Д; Массероли, М (2015). «Программный пакет для прогнозирования аннотаций генов и белков и поиска сходства» . Транзакции IEEE/ACM по вычислительной биологии и биоинформатике . 12 (4): 837–843. дои : 10.1109/TCBB.2014.2382127 . hdl : 11311/959408 . ПМИД 26357324 . S2CID 14714823 .
- ^ Фан, Кентукки (1951). «Максимальные свойства и неравенства для собственных значений вполне непрерывных операторов» . Труды Национальной академии наук Соединенных Штатов Америки . 37 (11): 760–766. Бибкод : 1951PNAS...37..760F . дои : 10.1073/pnas.37.11.760 . ПМЦ 1063464 . ПМИД 16578416 .
- ^ Ульманн, Джеффри (2018), Обобщенная обратная матрица, согласующаяся с диагональными преобразованиями (PDF) , SIAM Journal on Matrix Analysis, vol. 239, стр. 781–800, заархивировано из оригинала (PDF) 7 марта 2019 г.
- ^ Эккарт, К .; Янг, Г. (1936). «Приближение одной матрицы другой меньшего ранга». Психометрика . 1 (3): 211–8. дои : 10.1007/BF02288367 . S2CID 10163399 .
- ^ Хестенес, MR (1958). «Обращение матриц путем биортогонализации и связанные с этим результаты». Журнал Общества промышленной и прикладной математики . 6 (1): 51–90. дои : 10.1137/0106005 . JSTOR 2098862 . МР 0092215 .
- ^ ( Голуб и Кахан 1965 )
- ^ Голуб, Г.Х .; Рейнш, К. (1970). «Разложение по сингулярным значениям и решения методом наименьших квадратов». Численная математика . 14 (5): 403–420. дои : 10.1007/BF02163027 . МР1553974 . S2CID 123532178 .
Ссылки [ править ]
- Банерджи, Судипто; Рой, Аниндья (2014), Линейная алгебра и матричный анализ для статистики , Тексты по статистическим наукам (1-е изд.), Чепмен и Холл / CRC, ISBN 978-1420095388
- Бисгард, Джеймс (2021). Анализ и линейная алгебра: разложение по сингулярным значениям и приложения . Студенческая математическая библиотека (1-е изд.). АМС. ISBN 978-1-4704-6332-8 .
- Чикко, Д; Массероли, М (2015). «Программный пакет для прогнозирования аннотаций генов и белков и поиска сходства» . Транзакции IEEE/ACM по вычислительной биологии и биоинформатике . 12 (4): 837–843. дои : 10.1109/TCBB.2014.2382127 . hdl : 11311/959408 . ПМИД 26357324 . S2CID 14714823 .
- Трефетен, Ллойд Н .; Бау III, Дэвид (1997). Численная линейная алгебра . Филадельфия: Общество промышленной и прикладной математики. ISBN 978-0-89871-361-9 .
- Деммель, Джеймс ; Кахан, Уильям (1990). «Точные сингулярные значения двудиагональных матриц». Журнал SIAM по научным и статистическим вычислениям . 11 (5): 873–912. CiteSeerX 10.1.1.48.3740 . дои : 10.1137/0911052 .
- Голуб, Джин Х .; Кахан, Уильям (1965). «Вычисление сингулярных значений и псевдообратной матрицы». Журнал Общества промышленной и прикладной математики, серия B: Численный анализ . 2 (2): 205–224. Бибкод : 1965SJNA....2..205G . дои : 10.1137/0702016 . JSTOR 2949777 .
- Голуб, Джин Х .; Ван Лоан, Чарльз Ф. (1996). Матричные вычисления (3-е изд.). Джонс Хопкинс. ISBN 978-0-8018-5414-9 .
- Команда GSL (2007). «§14.4 Разложение по сингулярным значениям» . Научная библиотека ГНУ. Справочное руководство .
- Халлдор, Бьернссон и Венегас, Сильвия А. (1997). «Руководство по анализу климатических данных EOF и SVD» . Университет Макгилла, Отчет CCGCR № 97-1, Монреаль, Квебек, 52 стр.
- Хансен, ПК (1987). «Усеченный СВД как метод регуляризации». КУСОЧЕК . 27 (4): 534–553. дои : 10.1007/BF01937276 . S2CID 37591557 .
- Хорн, Роджер А.; Джонсон, Чарльз Р. (1985). «Раздел 7.3». Матричный анализ . Издательство Кембриджского университета. ISBN 978-0-521-38632-6 .
- Хорн, Роджер А.; Джонсон, Чарльз Р. (1991). «Глава 3» . Темы матричного анализа . Издательство Кембриджского университета. ISBN 978-0-521-46713-1 .
- Самет, Х. (2006). Основы многомерных и метрических структур данных . Морган Кауфманн. ISBN 978-0-12-369446-1 .
- Стрэнг Г. (1998). «Раздел 6.7». Введение в линейную алгебру (3-е изд.). Уэлсли-Кембридж Пресс. ISBN 978-0-9614088-5-5 .
- Стюарт, GW (1993). «О ранней истории разложения сингулярных значений» . Обзор СИАМ . 35 (4): 551–566. CiteSeerX 10.1.1.23.1831 . дои : 10.1137/1035134 . HDL : 1903/566 . JSTOR 2132388 .
- Уолл, Майкл Э.; Рехтштайнер, Андреас; Роча, Луис М. (2003). «Разложение по сингулярным значениям и анализ главных компонент» . В ДП Беррар; В. Дубицкий; М. Гранцов (ред.). Практический подход к анализу данных микрочипов . Норвелл, Массачусетс: Клювер. стр. 91–109.
- Пресс, WH; Теукольский, С.А.; Феттерлинг, WT; Фланнери, BP (2007), «Раздел 2.6» , Численные рецепты: искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN 978-0-521-88068-8








































































![{\displaystyle {\begin{aligned}\mathbf {U} &={\begin{bmatrix}\color {Green}0&\color {Blue}-1&\color {Cyan}0&\color {Emerald}0\\\ цвет {Зеленый}-1&\color {Синий}0&\color {Голубой}0&\color {Изумрудный}0\\\color {Зеленый}0&\color {Синий}0&\color {Голубой}0&\color {Изумрудный}- 1\\\color {Зеленый}0&\color {Синий}0&\color {Голубой}-1&\color {Изумруд}0\end{bmatrix}}\\[6pt]\mathbf {\Sigma } &={\begin {bmatrix}3&0&0&0&\color {Gray}{\mathit {0}}\\0&{\sqrt {5}}&0&0&\color {Gray}{\mathit {0}}\\0&0&2&0&\color {Gray}{\mathit {0}}\\0&0&0&\color {Red}\mathbf {0} &\color {Gray}{\mathit {0}}\end{bmatrix}}\\[6pt]\mathbf {V} ^{*} &={\begin{bmatrix}\color {Фиолетовый}0&\color {Фиолетовый}0&\color {Фиолетовый}-1&\color {Фиолетовый}0&\color {Фиолетовый}0\\\color {Сливовый}-{\sqrt {0.2}}&\color {Слива}0&\color {Слива}0&\color {Слива}0&\color {Слива}-{\sqrt {0.8}}\\\color {Пурпурный}0&\color {Пурпурный}- 1&\color {Пурпурный}0&\color {Пурпурный}0&\color {Пурпурный}0\\\color {Орхидея}0&\color {Орхидея}0&\color {Орхидея}0&\color {Орхидея}1&\color {Орхидея} 0\\\color {Фиолетовый}-{\sqrt {0.8}}&\color {Фиолетовый}0&\color {Фиолетовый}0&\color {Фиолетовый}0&\color {Фиолетовый}{\sqrt {0.2}}\end{ bmatrix}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c98ad3dd760d4b25f274add6c40e8412d351976a)
![{\displaystyle {\begin{aligned}\mathbf {U} \mathbf {U} ^{*}&={\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}}=\mathbf {I} _{4}\\[6pt]\mathbf {V} \mathbf {V} ^{*}&={\begin{bmatrix}1&0&0&0&0\\0&1&0&0&0\\0&0&1&0&0\\0&0&0&1&0\\0&0&0&0&1\end{ bmatrix}}=\mathbf {I} _{5}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47909bf34c8f6bf555462da282152e537800e0b2)




![{\displaystyle {\begin{aligned}\mathbf {Mv} &=\sigma \mathbf {u} ,\\[3mu]\mathbf {M} ^{*}\mathbf {u} &=\sigma \mathbf { v} .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ef40237646a1b9680a40c90fb157936cee0ad1d)















![{\displaystyle {\begin{aligned}\mathbf {M} ^{*}\mathbf {M} &=\mathbf {V} \mathbf {\Sigma } ^{*}\mathbf {U} ^{*}\ ,\mathbf {U} \mathbf {\Sigma } \mathbf {V} ^{*}=\mathbf {V} (\mathbf {\Sigma } ^{*}\mathbf {\Sigma } )\mathbf {V} ^{*},\\[3mu]\mathbf {M} \mathbf {M} ^{*}&=\mathbf {U} \mathbf {\Sigma } \mathbf {V} ^{*}\,\mathbf {V} \mathbf {\Sigma } ^{*}\mathbf {U} ^{*}=\mathbf {U} (\mathbf {\Sigma } \mathbf {\Sigma } ^{*})\mathbf {U } ^{*}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f02e41f55548643d74b09b78124e6ab72ab72a13)




















































































































































































































