Кокернел

Коядро f линейного отображения векторных пространств $f : X \to Y$ — это пространство $Y /im() кодобласти$ f по фактор $f$ образу $-$ . коядра называется корангом f $.$ Размерность

Коядра двойственны ядрам теории категорий , отсюда и название: ядро — это подобъект домена (оно отображается в домен), а коядро — это фактор-объект кодомена (оно отображается из кодомена).

Интуитивно, учитывая уравнение $f (x) = y$ , которое нужно решить, коядро измеряет ограничения , которым $y$ должно удовлетворять, чтобы это уравнение имело решение – препятствия на пути к решению – в то время как ядро измеряет степени свободы в решение, если оно существует. Это развито интуитивно , ниже.

В более общем смысле, коядро морфизма f $: X \to Y в$ некоторой категории (например, гомоморфизм между группами или ограниченный линейный оператор между гильбертовыми пространствами ) — это объект $Q$ и морфизм $q : Y \to Q$ такие, что композиция $qf$ является нулевой морфизм категории, причем $относительно$ этого q универсален свойства. отображение $q$ Часто понимают $, а само Q$ называют коядром $f$ .

Во многих ситуациях в абстрактной алгебре , например, для групп , пространств или модулей , коядро гомоморфизма $f : X \to Y$ является фактором Y $абелевых$ по образу f $векторных$ . В топологических условиях, например, с ограниченными линейными операторами между гильбертовыми пространствами, перед переходом к фактору обычно приходится замыкать изображение .

Формальное определение [ править ]

Коядро можно определить в общих рамках теории категорий . Чтобы определение имело смысл, рассматриваемая категория должна иметь нулевые морфизмы . Коядро → морфизма f $f : X 0 Y$ определяется коэквалайзер морфизма $Y$ нулевого $\to XY : X и как$ .

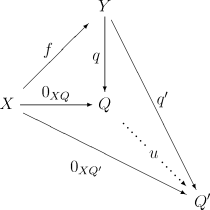
В явном виде это означает следующее. Коядро $f : X \to Y$ — это объект $Q$ вместе с морфизмом $q : Y \to Q$ таким, что диаграмма

ездит на работу . Более того, морфизм $q$ должен быть универсальным для этой диаграммы, т.е. любой другой такой $q' : Y \to Q'$ можно получить, составив $q$ с единственным морфизмом $u : Q \to Q'$ :

Как и во всех универсальных конструкциях, коядро, если оно существует, уникально с точностью до единственного изоморфизма , или, точнее: если $q : Y \to Q$ и $q' : Y \to Q'$ являются двумя коядрами $f : X \to Y$ , то существует единственный изоморфизм $u : Q \to Q'$ с $q' = u q$ .

Как и все коэквалайзеры, коядро $q : Y \to Q$ обязательно является эпиморфизмом . И наоборот, эпиморфизм называется нормальным (или конормальным ), если он является коядром некоторого морфизма. Категория называется конормальной , если каждый эпиморфизм нормален (например, категория групп конормальна).

Примеры [ править ]

В категории групп коядром гомоморфизма $f : G \to H$ является фактор H $f$ по нормальному замыканию образа $группового$ . В случае абелевых групп , поскольку каждая подгруппа нормальна, коядро — это просто $H$ по модулю образа $f$ :

\operatorname {coker} (f)=H/\operatorname {im} (f).

Особые случаи [ править ]

В преаддитивной категории имеет смысл добавлять и вычитать морфизмы. В такой категории коэквалайзер двух морфизмов $f$ и $g$ (если он существует) является всего лишь коядром их разности:

\operatorname {coeq} (f,g)=\operatorname {coker} (g-f).

В абелевой категории (специальный вид предаддитивной категории) образ и кообраз морфизма $f$ задаются формулой

{\begin{aligned}\operatorname {im} (f)&=\ker(\operatorname {coker} f),\\\operatorname {coim} (f)&=\operatorname {coker} (\ker f).\end{aligned}}

В частности, каждая абелева категория нормальна (а также конормальна). То есть каждый мономорфизм $m$ можно записать как ядро некоторого морфизма. В частности, $m$ — это ядро собственного коядра:

m=\ker(\operatorname {coker} (m))

Интуиция [ править ]

Коядро можно рассматривать как пространство ограничений , которым должно удовлетворять уравнение, как пространство препятствий , точно так же, как ядро — это пространство решений.

Формально ядро и коядро отображения $T : V \to W$ можно связать точной последовательностью

0\to \ker T\to V{\overset {T}{\longrightarrow }}W\to \operatorname {coker} T\to 0.

Их можно интерпретировать следующим образом: учитывая линейное уравнение $T (v) = w$ , которое нужно решить,

ядро — это пространство решений однородного ) уравнения $T (v) = 0$ , а его размерность — число степеней свободы решений $T (v = w$ , если они существуют;
коядро — это пространство ограничений на w , которые должны быть удовлетворены, чтобы уравнение имело решение, а его размерность — это количество независимых ограничений, которые должны быть удовлетворены, чтобы уравнение имело решение.

Размерность коядра плюс размерность изображения (ранг) в сумме дают размерность целевого пространства, поскольку размерность факторпространства $W / T (V)$ — это просто размерность пространства минус размерность изображение.

В качестве простого примера рассмотрим отображение $T : R 2 \to Р 2$ , заданный формулой $Т (Икс, y) знак равно (0, y)$ . Тогда для того, чтобы уравнение $T (x, y) = (a, b)$ имело решение, мы должны иметь $a = 0$ (одно ограничение), и в этом случае пространство решения равно $(x, b)$ или, что то же самое, $( 0, b) + (x, 0)$ , (одна степень свободы). Ядро можно выразить как подпространство $(x, 0) \subseteq V$ : значение $x$ — это свобода решения. Коядро может быть выражено через действительнозначное отображение $W : (a, b) \to (a)$ : для данного вектора $(a, b)$ значение $a$ является препятствием для существования решения.

Кроме того, коядро можно рассматривать как нечто, что «обнаруживает» сюръективы точно так же, как ядро «обнаруживает» инъекции . Отображение инъективно тогда и только тогда, когда его ядро тривиально, а отображение сюръективно тогда и только тогда, когда его коядро тривиально, или, другими словами, если $W = im(T)$ .

Ссылки [ править ]

Сондерс Мак Лейн : Категории для работающего математика , второе издание, 1978, стр. 64
Эмили Риль : Теория категорий в контексте , Aurora Modern Math Originals , 2014, стр. 82, с. 139 сноска 8.