Симметричная моноидальная категория

В теории категорий , разделе математики , симметричная моноидальная категория — это моноидальная категория (т. е. категория, в которой «тензорное произведение» $\otimes$ определено) такое, что тензорное произведение симметрично (т.е. $A\otimes B$ в определенном строгом смысле естественно изоморфен $B\otimes A$ для всех объектов $A$ и $B$ категории). Одним из прототипических примеров симметричной моноидальной категории является категория векторных пространств над некоторым фиксированным полем k, использующая обычное тензорное произведение векторных пространств .

Определение [ править ]

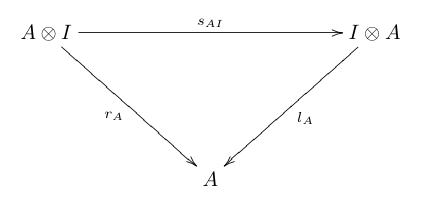
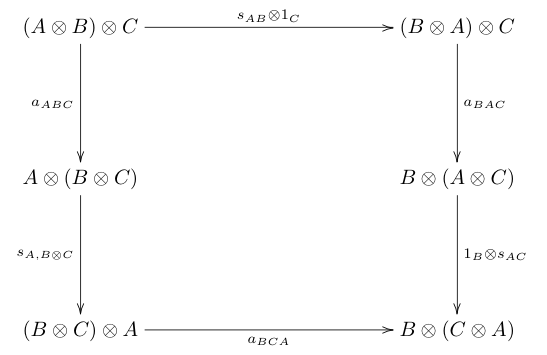
Симметричная моноидальная категория — это моноидальная категория ( C , ⊗, I ) такая, что для каждой пары A , B объектов в C существует изоморфизм $s_{AB}:A\otimes B\to B\otimes A$ называется картой подкачки ^[1] которое естественно как в A , так и в B и такое, что следующие диаграммы коммутируют:

Единичная согласованность:
Ассоциативная когерентность:
Обратный закон:

На диаграммах выше a , l и r представляют собой изоморфизм ассоциативности, левый единичный изоморфизм и правый единичный изоморфизм соответственно.

Примеры [ править ]

Некоторые примеры и непримеры симметричных моноидальных категорий:

Категория наборов . Тензорное произведение представляет собой теоретико-множественное декартово произведение, и любой одноэлементный элемент можно зафиксировать как единичный объект.
Категория групп . Как и раньше, тензорное произведение — это просто декартово произведение групп, а тривиальная группа — это единичный объект.
В более общем смысле, любая категория с конечными произведениями, то есть декартова моноидальная категория , является симметричной моноидальной. Тензорное произведение является прямым произведением объектов, а любой терминальный объект (пустое произведение) является единичным объектом.
Категория бимодулей над кольцом R моноидальна (с использованием обычного тензорного произведения модулей), но не обязательно симметрична. Если R коммутативен, категория левых R -модулей симметрична моноидальна. Последний примерный класс включает категорию всех векторных пространств над данным полем.
Учитывая поле k и группу (или алгебру Ли над k ), категория всех k -линейных представлений группы (или алгебры Ли) является симметричной моноидальной категорией. Здесь используется стандартное тензорное произведение представлений.
Категории ( Ste , $\circledast$ ) и ( Сте , $\odot$ ) стереотипных пространств над ${\mathbb {C} }$ симметричны моноидальны, причем ( Ste , $\circledast$ ) — замкнутая симметричная моноидальная категория с внутренним hom-функтором $\oslash$ .

Свойства [ править ]

Классифицирующее пространство (геометрическая реализация нерва ) симметричной моноидальной категории представляет собой $E_{\infty }$ пространство, поэтому его групповое завершение представляет собой пространство бесконечного цикла . ^[2]

Специализации [ править ]

Симметричная моноидальная категория кинжала — это симметричная моноидальная категория с совместимой структурой кинжала .

Космос . — это полная кополная замкнутая симметричная моноидальная категория

Обобщения [ править ]

В симметричной моноидальной категории естественные изоморфизмы $s_{AB}:A\otimes B\to B\otimes A$ являются своими собственными обратными сторонами в том смысле, что $s_{BA}\circ s_{AB}=1_{A\otimes B}$ . Если мы откажемся от этого требования (но по-прежнему будем требовать, чтобы $A\otimes B$ быть естественно изоморфным $B\otimes A$ ), получаем более общее понятие сплетенной моноидальной категории .

Ссылки [ править ]

^ Фонг, Брендан; Спивак, Дэвид И. (12 октября 2018 г.). «Семь очерков композиционности: приглашение к прикладной теории категорий». arXiv : 1803.05316 [ мат.CT ].
^ Томасон, RW (1995). «Симметричные моноидальные категории моделируют все соединительные спектры» (PDF) . Теория и приложения категорий . 1 (5): 78–118. CiteSeerX 10.1.1.501.2534 .

Симметричная моноидальная категория в n Lab
Эта статья включает в себя материал из категории «Симметричные моноиды» на сайте PlanetMath , который доступен под лицензией Creative Commons Attribution/Share-Alike License .

[1] Фонг, Брендан; Спивак, Дэвид И. (12 октября 2018 г.). «Семь очерков композиционности: приглашение к прикладной теории категорий». arXiv : 1803.05316 [ мат.CT ].

[2] Томасон, RW (1995). «Симметричные моноидальные категории моделируют все соединительные спектры» (PDF) . Теория и приложения категорий . 1 (5): 78–118. CiteSeerX 10.1.1.501.2534 .

[1]

[2]