Продукт (теория категорий)

В теории категорий произведение понятие , двух (или более) объектов в категории призванное уловить суть конструкций в других областях математики, как декартово произведение множеств таких , прямое произведение групп — это или колец и произведение топологических пространств . По сути, продукт семейства объектов — это «наиболее общий» объект, допускающий морфизм к каждому из данных объектов.

Определение [ править ]

Произведение двух объектов [ править ]

Исправить категорию $C.$ Позволять $X_{1}$ и $X_{2}$ быть объектами $C.$ Продукт $X_{1}$ и $X_{2}$ это объект $X,$ обычно обозначается $X_{1}\times X_{2},$ оснащен парой морфизмов $\pi _{1}:X\to X_{1},$ $\pi _{2}:X\to X_{2}$ удовлетворяющее следующему универсальному свойству :

Для каждого объекта $Y$ и каждая пара морфизмов $f_{1}:Y\to X_{1},$ $f_{2}:Y\to X_{2},$ существует единственный морфизм $f:Y\to X_{1}\times X_{2}$ такая, что следующая диаграмма коммутирует :
Universal property of the product

Существует ли продукт, может зависеть от $C$ или на $X_{1}$ и $X_{2}.$ Если он существует, то он уникален с точностью до канонического изоморфизма из-за универсального свойства, поэтому можно говорить о произведении . Это имеет следующий смысл: если $X',\pi _{1}',\pi _{2}'$ является другим произведением, существует единственный изоморфизм $h:X'\to X_{1}\times X_{2}$ такой, что $\pi _{1}'=\pi _{1}\circ h$ и $\pi _{2}'=\pi _{2}\circ h$ .

Морфизмы $\pi _{1}$ и $\pi _{2}$ называются каноническими проекциями или морфизмами проекций ; письмо $\pi$ аллитерирует с проекцией. Данный $Y$ и $f_{1},$ $f_{2},$ уникальный морфизм $f$ называется произведением морфизмов $f_{1}$ и $f_{2}$ и обозначается $\langle f_{1},f_{2}\rangle .$

Продукт произвольного семейства [ править ]

Вместо двух объектов мы можем начать с произвольного семейства объектов, индексированного набором $I.$

Учитывая семью $\left(X_{i}\right)_{i\in I}$ объектов, продукт семейства является объектом $X$ снабженный морфизмами $\pi _{i}:X\to X_{i},$ удовлетворяющее следующему универсальному свойству:

Для каждого объекта $Y$ и каждый $I$ -индексированное семейство морфизмов $f_{i}:Y\to X_{i},$ существует единственный морфизм $f:Y\to X$ такие, что следующие диаграммы коммутируют для всех $i\in I:$
Universal product of the product

Товар обозначается $\prod _{i\in I}X_{i}.$ Если $I=\{1,\ldots ,n\},$ тогда это обозначается $X_{1}\times \cdots \times X_{n}$ а произведение морфизмов обозначается $\langle f_{1},\ldots ,f_{n}\rangle .$

Уравненное определение [ править ]

Альтернативно, продукт может быть определен с помощью уравнений. Так, например, для бинарного продукта:

Существование $f$ гарантируется существованием операции $\langle \cdot ,\cdot \rangle .$
Коммутативность приведенных выше диаграмм гарантируется равенством: для всех $f_{1},f_{2}$ и все $i\in \{1,2\},$ $\pi _{i}\circ \left\langle f_{1},f_{2}\right\rangle =f_{i}$
Уникальность $f$ гарантируется равенство: для всех $g:Y\to X_{1}\times X_{2},$ $\left\langle \pi _{1}\circ g,\pi _{2}\circ g\right\rangle =g.$ ^[1]

В качестве ограничения [ править ]

Произведение представляет собой частный случай предела . В этом можно убедиться, используя дискретную категорию (семейство объектов без каких-либо морфизмов, кроме их тождественных морфизмов) в качестве диаграммы, необходимой для определения предела. Дискретные объекты будут служить индексом компонентов и проекций. Если рассматривать эту диаграмму как функтор, то это функтор из набора индексов $I$ рассматривается как дискретная категория. Определение произведения тогда совпадает с определением предела, $\{f\}_{i}$ является конусом , а проекции являются пределом (предельным конусом).

Универсальная собственность [ править ]

Как предел является частным случаем универсальной конструкции , так и произведение. Исходя из определения универсального свойства пределов , возьмем $\mathbf {J}$ как дискретная категория с двумя объектами, так что $\mathbf {C} ^{\mathbf {J} }$ это просто категория продукта $\mathbf {C} \times \mathbf {C} .$ Диагональный функтор $\Delta :\mathbf {C} \to \mathbf {C} \times \mathbf {C}$ присваивается каждому объекту $X$ заказанная пара $(X,X)$ и каждому морфизму $f$ пара $(f,f).$ Продукт $X_{1}\times X_{2}$ в $C$ задается универсальным морфизмом функтора $\Delta$ на объект $\left(X_{1},X_{2}\right)$ в $\mathbf {C} \times \mathbf {C} .$ Этот универсальный морфизм состоит из объекта $X$ из $C$ и морфизм $(X,X)\to \left(X_{1},X_{2}\right)$ который содержит проекции.

Примеры [ править ]

В категории множеств продукт (в теоретическом смысле категорий) является декартовым произведением. Учитывая семейство множеств $X_{i}$ продукт определяется как

\prod _{i\in I}X_{i}:=\left\{\left(x_{i}\right)_{i\in I}:x_{i}\in X_{i}{\text{ for all }}i\in I\right\}

с каноническими проекциями

\pi _{j}:\prod _{i\in I}X_{i}\to X_{j},\quad \pi _{j}\left(\left(x_{i}\right)_{i\in I}\right):=x_{j}.

Учитывая любой набор

Y

с семейством функций

f_{i}:Y\to X_{i},

универсальная стрела

f:Y\to \prod _{i\in I}X_{i}

определяется

f(y):=\left(f_{i}(y)\right)_{i\in I}.

Другие примеры:

В категории топологических пространств продуктом является пространство, базовым множеством которого является декартово произведение и которое несет в себе топологию произведения . Топология произведения — это самая грубая топология , для которой все проекции непрерывны .
В категории модулей над некоторым кольцом $R,$ произведение представляет собой декартово произведение с покомпонентным сложением и распределительным умножением.
В категории групп продукт является прямым произведением групп, заданных декартовым произведением с умножением, определенным покомпонентно.
В категории графов продуктом является тензорное произведение графов .
В категории отношений продукт дается непересекающимся объединением . (Это может показаться некоторым сюрпризом, учитывая, что категория множеств является подкатегорией категории отношений.)
В категории алгебраических многообразий произведение задается вложением Сегре .
В категории полуабелевых моноидов произведение задаётся историческим моноидом .
В категории банаховых пространств и коротких отображений произведение имеет $l \infty$ норма. ^[2]
можно Частично упорядоченное множество рассматривать как категорию, используя отношение порядка в качестве морфизмов. В этом случае продукты и сопутствующие продукты соответствуют наибольшим нижним границам ( встречается ) и наименьшим верхним границам ( объединениям ).

Обсуждение [ править ]

Пример, в котором товар не существует: В категории полей товар $\mathbb {Q} \times F_{p}$ не существует, поскольку не существует поля с гомоморфизмами обоим $\mathbb {Q}$ и $F_{p}.$

Другой пример: пустой продукт (т. е. $I$ — пустое множество ) — то же самое, что терминальный объект , а некоторые категории, такие как категория бесконечных групп, не имеют терминального объекта: учитывая любую бесконечную группу $G$ существует бесконечно много морфизмов $\mathbb {Z} \to G,$ так $G$ не может быть терминальным.

Если $I$ представляет собой набор, в котором все продукты для семей индексируются с помощью $I$ существуют, то каждое произведение можно рассматривать как функтор $\mathbf {C} ^{I}\to \mathbf {C} .$ ^[3]То, как этот функтор отображает объекты, очевидно. Отображение морфизмов является тонким, потому что произведение морфизмов, определенных выше, не подходит. Сначала рассмотрим функтор двоичного произведения, который является бифунктором . Для $f_{1}:X_{1}\to Y_{1},f_{2}:X_{2}\to Y_{2}$ нам нужно найти морфизм $X_{1}\times X_{2}\to Y_{1}\times Y_{2}.$ Мы выбираем $\left\langle f_{1}\circ \pi _{1},f_{2}\circ \pi _{2}\right\rangle .$ Эта операция над морфизмами называется декартовым произведением морфизмов . ^[4]Во-вторых, рассмотрим общий функтор произведения. Для семей $\left\{X\right\}_{i},\left\{Y\right\}_{i},f_{i}:X_{i}\to Y_{i}$ нам нужно найти морфизм $\prod _{i\in I}X_{i}\to \prod _{i\in I}Y_{i}.$ Выбираем произведение морфизмов $\left\{f_{i}\circ \pi _{i}\right\}_{i}.$

Категория, в которой каждое конечное множество объектов имеет произведение, иногда называется декартовой категорией. ^[4] (хотя некоторые авторы используют эту фразу в значении «категория со всеми конечными пределами»).

Продукт ассоциативен . Предполагать $C$ является декартовой категорией, функторы-продукты выбраны, как указано выше, и $1$ обозначает конечный объект $C.$ Тогда мы имеем естественные изоморфизмы

X\times (Y\times Z)\simeq (X\times Y)\times Z\simeq X\times Y\times Z,

X\times 1\simeq 1\times X\simeq X,

X\times Y\simeq Y\times X.

Эти свойства формально подобны свойствам коммутативного моноида ; Декартова категория с ее конечными произведениями является примером симметричной моноидальной категории .

Дистрибутивность [ править ]

Для любых объектов $X,Y,{\text{ and }}Z$ категории с конечными произведениями и копроизведениями существует канонический морфизм $X\times Y+X\times Z\to X\times (Y+Z),$ где знак плюс здесь обозначает копроизведение . Чтобы убедиться в этом, заметим, что универсальное свойство копроизведения $X\times Y+X\times Z$ гарантирует существование уникальных стрелок, заполняющих следующую диаграмму (индуцированные стрелки пунктирны):

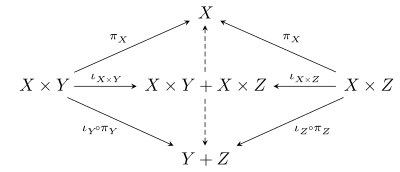
Универсальное свойство продукта $X\times (Y+Z)$ тогда гарантирует уникальный морфизм $X\times Y+X\times Z\to X\times (Y+Z)$ индуцированные пунктирными стрелками на диаграмме выше. Дистрибутивной категорией называется категория, в которой этот морфизм на самом деле является изоморфизмом. Таким образом, в дистрибутивной категории существует канонический изоморфизм

X\times (Y+Z)\simeq (X\times Y)+(X\times Z).

См. также [ править ]

Копродукт – двойник продукта
Диагональный функтор – левый сопряженный функтору произведения.
Предел и копределы - математическая концепция
Эквалайзер — набор аргументов, в которых две или более функции имеют одинаковое значение.
Обратный предел - конструкция в теории категорий
Декартова замкнутая категория - Тип категории в теории категорий.
Категориальный возврат - наиболее общее завершение коммутативного квадрата с учетом двух морфизмов с одинаковым кодоменом.

Ссылки [ править ]

^ Ламбек Дж., Скотт П.Дж. (1988). Введение в категориальную логику высшего порядка . Издательство Кембриджского университета. п. 304.
^ Цяочу Юань (23 июня 2012 г.). «Банаховые пространства (и метрики Ловера, и закрытые категории)» . Раздражающая точность .
^ Лейн, С. Мак (1988). Категории для работающего математика (1-е изд.). Нью-Йорк: Springer-Verlag. п. 37. ИСБН 0-387-90035-7 .
^ Перейти обратно: ^а ^б Майкл Барр, Чарльз Уэллс (1999). Теория категорий – Конспекты лекций для ESSLLI . п. 62. Архивировано из оригинала 13 апреля 2011 г.

Адамек, Иржи; Хорст Херрлих; Джордж Э. Стрекер (1990). Абстрактные и конкретные категории (PDF) . Джон Уайли и сыновья. ISBN 0-471-60922-6 .
Барр, Майкл; Чарльз Уэллс (1999). Теория категорий для информатики (PDF) . Les Publications CRM Montreal (публикация PM023). Архивировано из оригинала (PDF) 4 марта 2016 г. Проверено 21 марта 2016 г. Глава 5.
Мак Лейн, Сондерс (1998). Категории для работающего математика . Тексты для аспирантов по математике 5 (2-е изд.). Спрингер. ISBN 0-387-98403-8 .
Определение 2.1.1 в Борсо, Фрэнсис (1994). Справочник по категориальной алгебре . Энциклопедия математики и ее приложений 50–51, 53 [т.е. 52]. Том. 1. Издательство Кембриджского университета. п. 39 . ISBN 0-521-44178-1 .

Внешние ссылки [ править ]

Интерактивная веб-страница , генерирующая примеры продуктов из категории конечных множеств. Автор Джоселин Пейн .
Продукт в n Lab

[1] Ламбек Дж., Скотт П.Дж. (1988). Введение в категориальную логику высшего порядка . Издательство Кембриджского университета. п. 304.

[Ban1Cat-2] Цяочу Юань (23 июня 2012 г.). «Банаховые пространства (и метрики Ловера, и закрытые категории)» . Раздражающая точность .

[3] Лейн, С. Мак (1988). Категории для работающего математика (1-е изд.). Нью-Йорк: Springer-Verlag. п. 37. ИСБН 0-387-90035-7 .

[esslli-4] Перейти обратно: ^а ^б Майкл Барр, Чарльз Уэллс (1999). Теория категорий – Конспекты лекций для ESSLLI . п. 62. Архивировано из оригинала 13 апреля 2011 г.

[1]

[2]

[3]

[4]