Пустой набор

«∅» перенаправляется сюда. Похожие символы см. в Ø (значения) .

Чтобы узнать о других значениях слова «Пустой», см. «Пусто (значения)» .

Пустое множество — это множество, не содержащее элементов.

В математике пустое множество — это уникальное множество , не содержащее элементов ; его размер или мощность (количество элементов в наборе) равны нулю . Некоторые аксиоматические теории множеств гарантируют, что пустое множество существует, включая аксиому пустого множества , в то время как в других теориях его существование может быть выведено. Многие возможные свойства множеств бессмысленно верны для пустого множества.

Любое множество, кроме пустого, называется непустым.

В некоторых учебниках и популяризациях пустой набор называется «нулевым набором». Однако нулевое множество — это отдельное понятие в контексте теории меры , в которой оно описывает множество нулевой меры (которое не обязательно пусто).

Обозначения

Символ пустого множества

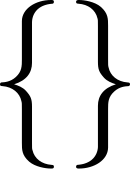
Общие обозначения пустого набора включают «{ }», « $\emptyset$", и " ∅ ". Последние два символа были введены группой Бурбаки (в частности, Андре Вейлем ) в 1939 году, вдохновленные буквой Ø ( U+00D8 Ø ЛАТИНСКАЯ ЗАГЛАВНАЯ БУКВА O СО Штрихом ) в датском и норвежском алфавитах. В прошлом «0» (цифра ноль ) иногда использовалась как символ пустого множества, но теперь это считается неправильным использованием обозначения.

Символ ∅ доступен в Unicode . пункте U+2205 ∅ ПУСТОЙ НАБОР . Его можно закодировать в HTML как ∅ и в качестве ∅ или как ∅. Его можно закодировать в LaTeX как \varnothing. Символ $\emptyset$ кодируется в LaTeX как \emptyset.

При написании на таких языках, как датский и норвежский, где символ пустого набора можно спутать с буквой Ø (как при использовании этого символа в лингвистике), вместо него можно использовать символ Юникода U+29B0 REVERSED EMPTY SET ⦰.

Свойства

В стандартной аксиоматической теории множеств , согласно принципу экстенсиональности , два множества равны, если они имеют одинаковые элементы (то есть ни в одном из них нет элемента, которого нет в другом). В результате может быть только один набор без элементов, поэтому используется термин «пустой набор», а не «пустой набор».

Единственное подмножество пустого множества — это само пустое множество; эквивалентно, набор мощности пустого набора - это набор, содержащий только пустой набор. Число элементов пустого множества (т. е. его мощность ) равно нулю. Пустой набор — единственный набор, обладающий любым из этих свойств.

Для любого набора А :

• Пустое множество подмножеством A является
• Объединение с A A пустым множеством есть
• Пересечение . A с пустым множеством является пустым множеством
• Декартово произведение A . и пустого множества — это пустое множество

Для любого свойства P :

• Для каждого элемента $\varnothing$, свойство P имеет место ( пустая истина ).
• Нет никакого элемента $\varnothing$ свойство P. для которого выполнено

И наоборот, если для некоторого свойства P и некоторого множества V справедливы следующие два утверждения:

• Для каждого элемента V свойство P. имеет место
• Не существует элемента V свойство P. , для которого выполнено

затем $V=\varnothing .$

По определению подмножества пустое множество является подмножеством любого A. множества То есть каждый элемент x из $\varnothing$принадлежит А. ​ Действительно, если бы не было правдой, что каждый элемент $\varnothing$ находится в A , то будет хотя бы один элемент $\varnothing$чего нет А. в Поскольку отсутствуют элементы $\varnothing$ вообще нет никакого элемента $\varnothing$этого нет А. в Любое утверждение, начинающееся со слов «для каждого элемента $\varnothing$«не делает никаких существенных утверждений; это пустая истина . Это часто перефразируют как «все верно для элементов пустого множества».

В обычном теоретико-множественном определении натуральных чисел ноль моделируется пустым множеством.

Операции над пустым множеством

Говоря о сумме элементов конечного множества, неизбежно приходим к соглашению, что сумма элементов пустого множества ( пустая сумма ) равна нулю. Причина этого в том, что нуль является единичным элементом сложения. Аналогично, произведение элементов пустого множества ( пустое произведение ) следует считать равным единице , поскольку единица является единичным элементом для умножения.

Расстройство — это перестановка множества без неподвижных точек . Пустое множество само по себе можно считать нарушением, поскольку оно имеет только одну перестановку ( $0!=1$), и совершенно неверно, что не может быть найден ни один элемент (пустого множества), который сохранял бы свое исходное положение.

В других областях математики

Расширенные действительные числа

Поскольку пустое множество не имеет члена, когда оно рассматривается как подмножество любого упорядоченного набора , каждый член этого набора будет верхней и нижней границей пустого набора. Например, если рассматривать его как подмножество действительных чисел с его обычным порядком, представленным линией действительных чисел , каждое действительное число является одновременно верхней и нижней границей пустого набора. Если рассматривать его как подмножество расширенных действительных чисел , образованных добавлением двух «числ» или «точек» к действительным числам (а именно, отрицательной бесконечности , обозначаемой $-\infty \!\,,$ которое определяется как меньше любого другого расширенного действительного числа, и положительная бесконечность , обозначаемая $+\infty \!\,,$ которое определено как большее, чем любое другое расширенное действительное число), мы имеем следующее:

$$\sup \varnothing =\min(\{-\infty ,+\infty \}\cup \mathbb {R} )=-\infty ,$$

и

$$\inf \varnothing =\max(\{-\infty ,+\infty \}\cup \mathbb {R} )=+\infty .$$

То есть наименьшая верхняя граница (sup или supremum ) пустого набора — это отрицательная бесконечность, а наибольшая нижняя граница (inf или infimum ) — положительная бесконечность. По аналогии с вышеизложенным, в области расширенных действительных чисел отрицательная бесконечность является единицей для операторов максимума и верхней границы, а положительная бесконечность является единицей для операторов минимума и нижней границы.

Топология

В любом топологическом пространстве X пустое множество открыто по определению, как и X . Поскольку дополнение к открытому множеству закрыто , а пустое множество и X являются дополнениями друг друга, пустое множество также закрыто, что делает его открыто-открытым множеством . Более того, пустое множество компактно в силу того, что каждое конечное множество компактно.

Замыкание . пустого множества пусто Это известно как «сохранение нулевых союзов ».

Теория категорий

Если $A$ множество, то существует ровно одна функция $f$ от $\varnothing$ к $A,$пустая функция . В результате пустое множество является единственным исходным объектом категории множеств и функций.

Пустое множество можно превратить в топологическое пространство , называемое пустым пространством, только одним способом: определив пустое множество как открытое . Это пустое топологическое пространство является единственным исходным объектом в категории топологических пространств с непрерывными отображениями . Фактически, это строгий исходный объект : только пустое множество имеет функцию для пустого множества.

Теория множеств

В конструкции фон Неймана ординалов 0 определяется как пустое множество, а последующий ординал определяется как $S(\alpha )=\alpha \cup \{\alpha \}$. Таким образом, мы имеем $0=\varnothing$, $1=0\cup \{0\}=\{\varnothing \}$, $2=1\cup \{1\}=\{\varnothing ,\{\varnothing \}\}$, и так далее. Конструкция фон Неймана вместе с аксиомой бесконечности , гарантирующей существование хотя бы одного бесконечного множества, может быть использована для построения множества натуральных чисел: $\mathbb {N} _{0}$, такие, что аксиомы арифметики Пеано выполняются .

Существование под сомнением

Исторические

В контексте наборов действительных чисел Кантор использовал $P\equiv O$ обозначать " $P$ не содержит ни одной точки». Это $\equiv O$обозначения использовались в определениях; например, Кантор определил два множества как непересекающиеся, если в их пересечении нет точек; однако остается спорным, рассматривал ли Кантор $O$ как существующее множество само по себе, или если Кантор просто использовал $\equiv O$как предикат пустоты. Цермело принял $O$ себя как набор, но считал его «неподходящим набором».

Аксиоматическая теория множеств

В теории множеств Цермело существование пустого множества обеспечивается аксиомой пустого множества , а его единственность следует из аксиомы экстенсиональности . Однако аксиому пустого множества можно показать избыточной как минимум двумя способами:

• Стандартная логика первого порядка подразумевает, просто исходя из логических аксиом , что что-то существует, и, говоря языком теории множеств, эта вещь должна быть множеством. Теперь существование пустого множества легко следует из аксиомы разделения .
• Даже используя свободную логику (которая логически не подразумевает, что что-то существует), уже существует аксиома, подразумевающая существование хотя бы одного множества, а именно аксиома бесконечности .

Философские проблемы

Хотя пустое множество является стандартной и широко распространенной математической концепцией, оно остается онтологической диковинкой, смысл и полезность которой обсуждаются философами и логиками.

Пустое множество — это не то же самое, что ничто ; скорее, это набор, внутри которого нет ничего, а набор — это всегда что-то . Эту проблему можно решить, рассматривая набор как сумку — пустая сумка, несомненно, все еще существует. Дарлинг (2004) объясняет, что пустое множество — это не ничто, а скорее «набор всех треугольников с четырьмя сторонами, набор всех чисел, которые больше девяти, но меньше восьми, и набор всех дебютных ходов в шахматах , которые привлечь короля ».

Популярный силлогизм

Нет ничего лучше, чем вечное счастье; бутерброд с ветчиной лучше, чем ничего; поэтому бутерброд с ветчиной лучше, чем вечное счастье

часто используется для демонстрации философской связи между концепцией ничего и пустым множеством. Дарлинг пишет, что контраст можно увидеть, переписав утверждения «Нет ничего лучше, чем вечное счастье» и «Сэндвич с ветчиной лучше, чем ничего» в математическом тоне. По словам Дарлинга, первое эквивалентно: «Набор всех вещей, которые лучше, чем вечное счастье, равен $\varnothing$", а последний - "Набор {сэндвич с ветчиной} лучше, чем набор $\varnothing$". Первый сравнивает элементы множеств, а второй сравнивает сами множества.

Джонатан Лоу утверждает, что, хотя пустое множество

несомненно, была важной вехой в истории математики… мы не должны предполагать, что ее полезность в вычислениях зависит от того, действительно ли она обозначает какой-то объект.

также имеет место следующее:

«Все, что нам когда-либо сообщали о пустом множестве, это то, что оно (1) является множеством, (2) не имеет членов и (3) является уникальным среди множеств, поскольку не имеет членов. Однако есть очень много вещей, которые не имеют членов в теоретико-множественном смысле, а именно, все не-множества. Совершенно ясно, почему эти вещи не имеют членов, поскольку они не являются множествами. Неясно, как может существовать единственное среди множеств. множество , не имеющее членов. Мы не можем вызвать к существованию такую ​​сущность простым условием».

Джордж Булос утверждал, что многое из того, что до сих пор было получено с помощью теории множеств, может быть так же легко получено путем количественной оценки множественного числа индивидов, без овеществления множеств как единичных сущностей, имеющих другие сущности в качестве членов.

См. также

• 0 — количество страниц, отображающих краткие описания без пробелов.
• Обитаемое множество - свойство множеств, используемых в конструктивной математике.
• Ничего – Полное отсутствие чего-либо; противоположность всему
• Набор мощности - математический набор, содержащий все подмножества данного набора.

Дальнейшее чтение

• Халмос, Пол , Наивная теория множеств . Принстон, Нью-Джерси: Компания Д. Ван Ностранда, 1960. Перепечатано Springer-Verlag, Нью-Йорк, 1974. ISBN   0-387-90092-6 (издание Springer-Verlag). Перепечатано издательством Martino Fine Books, 2011 г. ISBN   978-1-61427-131-4 (издание в мягкой обложке).
• Джех, Томас (2002). Теория множеств . Монографии Спрингера по математике (изд. 3-го тысячелетия). Спрингер. ISBN  3-540-44085-2 .
• Грэм, Малькольм (1975). Современная элементарная математика (2-е изд.). Харкорт Брейс Йованович . ISBN  0155610392 .

Внешние ссылки

• Вайсштейн, Эрик В. «Пустой набор» . Математический мир .