Отношение (математика)

В математике отношение может существовать, а может и в множестве не существовать между двумя заданными членами множества. Например, « меньше чем » — это отношение на множестве натуральных чисел ; оно справедливо, например, между значениями $1$ и $3$ (обозначенными как $1 < 3$ ), а также между $3$ и $4$ (обозначаемыми как $3 < 4$ ), но не между значениями $3$ и $1$ и не между $4$ и $4$ , т.е. , $3 < 1$ и $4 < 4$ оба оцениваются как ложные. Другой пример: « сестра » — это отношение на множестве всех людей, оно имеет место, например, между Марией Кюри и Брониславой Длуской , и наоборот. Члены множества не могут находиться в отношениях «в определенной степени» — они либо находятся в отношениях, либо нет.

Формально отношение $R$ над множеством $X$ рассматривать как набор упорядоченных пар $(x, y)$ членов $X.$ можно ^[1]Отношение $R$ сохраняется между $x$ и $y$ если $(x, y)$ является членом $R.$ , Например, отношение « меньше чем » для натуральных чисел представляет собой бесконечное множество $R less$ пар натуральных чисел, которое содержит как $(1,3),$ так и $(3,4)$ , но ни $(3,1)$ , ни $(4). ,4)$ . Отношение « является нетривиальным делителем » на множестве однозначных натуральных чисел достаточно мало, чтобы его можно было показать здесь: $R дв = { (2,4), (2,6), (2,8), (3,6), (3,9), (4,8) }$ ; например, $2$ является нетривиальным делителем $8$ , но не наоборот, следовательно, $(2,8) \in R dv$ , но $(8,2) \notin R dv$ .

Если $R$ — отношение, справедливое для $x$ и $y,$ часто пишут $xRy$ . Для большинства распространенных в математике отношений вводятся специальные символы, такие как « $<$ » для «меньше чем» и « $|$ » для «является нетривиальным делителем» и наиболее популярный « $=$ » для «равно» . Например, « $1 < 3$ », « $1$ меньше $3$ » и « $(1,3) \in R less$ » означают одно и то же; некоторые авторы также пишут « $(1,3) \in (<)$ ».

Исследуются различные свойства отношений. Отношение $R$ является рефлексивным, если $xRx$ выполняется для всех $x$ , и иррефлексивным, если $xRx$ выполняется ни для одного $x$ . Оно симметрично, если $xRy$ всегда подразумевает $yRx$ , и асимметрично, если $xRy$ подразумевает, что $yRx$ невозможно. Оно транзитивно, если $xRy$ и $yRz$ всегда влекут за собой $xRz$ . Например, « меньше чем » является иррефлексивным, асимметричным и транзитивным, но не рефлексивным и не симметричным. « сестра » является переходным, но не рефлексивным (например, Пьер Кюри не является сестрой самого себя), ни симметричным, ни асимметричным; хотя быть иррефлексивным или нет может быть вопросом определения (каждая женщина является сестрой самой себе?), « является предком » является транзитивным, а « является родителем » — нет. Известны математические теоремы о комбинациях свойств отношений, такие как «транзитивное отношение иррефлексивно тогда и только тогда, когда оно асимметрично».

Особое значение имеют отношения, удовлетворяющие определенным сочетаниям свойств. Частичный порядок — это рефлексивное, антисимметричное и транзитивное отношение. ^[2] Отношение эквивалентности — это отношение, которое является рефлексивным, симметричным и транзитивным, ^[3] Функция — это отношение , которое является однолистным и тотальным слева (см. ниже ). ^[4]^[5]

Поскольку отношения представляют собой множества, ими можно манипулировать с помощью операций над множествами, включая объединение , пересечение и дополнение , что приводит к алгебре множеств . Кроме того, исчисление отношений включает в себя операции взятия обратных и составления отношений . ^[6]^[7]^[8]

Вышеупомянутая концепция отношения ^[а] был обобщен, чтобы допустить отношения между членами двух разных множеств ( неоднородное отношение , такое как « лежат на » между множеством всех точек и множеством всех линий в геометрии), отношения между тремя или более множествами ( конечное отношение , такое как «человек $x$ живет в городе $y$ в момент времени $z$ " ) и отношения между классами ^[б] (например, « является элементом » в классе всех множеств, см. Бинарное отношение § Наборы и классы ).

Определение [ править ]

Для данного множества $X$ отношение $R$ над $X$ представляет собой набор упорядоченных пар элементов из $X$ , формально: $R \subseteq { (x, y) | Икс, у \in Икс}$ . ^[1]^[9]

Утверждение $(x, y) \in R$ читается как « $x$ - $R$ связано с $y$ » и записывается в инфиксной записи как $xRy$ . ^[6]^[7]Порядок элементов важен; если $x \neq y$ , то $yRx$ может быть истинным или ложным независимо от $xRy$ . Например, $3$ делит $9$ , но $9$ не делит $3$ .

Представление отношений [ править ]

и Икс	1	2	3	4	6	12
1
2
3
4
6
12
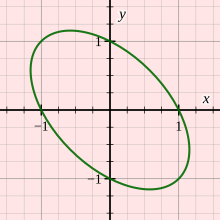
Представление $R div$ как булева матрица

Отношение $R$ на конечном множестве $X$ можно представить как:

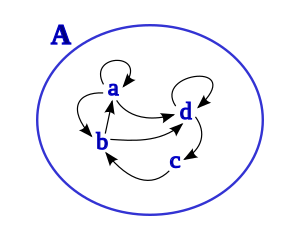
Ориентированный граф : каждый член $X$ соответствует вершине; направленное ребро из $x$ в $y$ существует тогда и только тогда, когда $x, y) \in R.$ (
Булева матрица : члены $X$ расположены в некоторой фиксированной последовательности $x 1$ , ..., $x n$ ; матрица имеет размеры $n \times n$ , причем элемент в строке $i$ , столбце $j$ равен , если $(x i, x j) \in R$ , и , в противном случае.
2D-график : как обобщение булевой матрицы, отношение на –бесконечном– множестве $R$ действительных чисел может быть представлено как двумерная геометрическая фигура: используя декартовы координаты , нарисуйте точку в $(x, y)$ всякий раз, когда $(Икс, у) \in р$ .

Переходный ^[с] отношение $R$ на конечном множестве $X$ можно также представить как

Диаграмма Хассе : каждый член $X$ соответствует вершине; направленные ребра рисуются так, что направленный путь от $x$ до $y$ существует тогда и только тогда, когда $(x, y) \in R$ . По сравнению с представлением в виде ориентированного графа, диаграмме Хассе требуется меньше ребер, что приводит к менее запутанному изображению. Поскольку отношение « существует направленный путь от $x$ до $y$ » транзитивно, в диаграммах Хассе могут быть представлены только транзитивные отношения. Обычно диаграмма строится так, что все ребра направлены вверх, а стрелки опущены.

Например, на множестве всех делителей числа $12$ определите отношение $R div$ по формуле

x R div y,

если

x

— делитель

y

и

x \neq y

.

Формально $X = { 1, 2, 3, 4, 6, 12 }$ и $R div = { (1,2), (1,3), (1,4), (1,6), (1,12). ), (2,4), (2,6), (2,12), (3,6), (3,12), (4,12), (6,12) }$ . Представление $R div$ в виде булевой матрицы показано в средней таблице; представление как в виде диаграммы Хассе, так и в виде ориентированного графа показано на левом рисунке.

Следующие действия эквивалентны:

$x R div y$ верно.
$(x, y) \in R div$ .
Путь от $x$ до $y$ существует в диаграмме Хассе, представляющей $R div$ .
Ребро от $x$ до $y$ существует в ориентированном графе, представляющем $R div$ .
В логической матрице, представляющей $R div$ , элемент в строке $x$ и столбце $y$ равен " ".

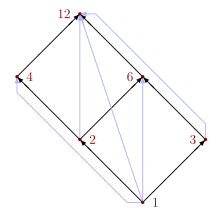
В качестве другого примера определите отношение $R el$ на $R$ следующим образом:

x R el y

, если

x 2 + ху + у 2 = 1

.

Представление $R el$ в виде 2D-графика имеет форму эллипса, см. рисунок справа. Поскольку $R$ не конечно, ни ориентированный граф, ни конечная булева матрица, ни диаграмма Хассе не могут быть использованы для изображения $R эл$ .

Свойства отношений [ править ]

Некоторые важные свойства, которыми может обладать отношение $R$ над множеством $X$ :

Рефлексивный: для всех $x \in X$ , $xRx$ . Например, $\geq$ — рефлексивное отношение, а $>$ — нет.

Иррефлексивный (или строгий ): для всех $x \in X$ , а не $xRx$ . Например, $>$ — иррефлексивное отношение, а $\geq$ — нет.

Предыдущие 2 альтернативы не являются исчерпывающими; например, красное соотношение $y = x 2$ приведенная на диаграмме ниже, не является ни иррефлексивной, ни рефлексивной, поскольку содержит пару $(0,0)$ , но не $(2,2)$ соответственно.

Симметричный: для всех $x, y \in X$ , если $xRy$ , то $yRx$ . Например, «является кровным родственником» является симметричным отношением, поскольку $x$ является кровным родственником $y$ тогда и только тогда, когда $y$ является кровным родственником $x$ .

антисимметричный: для всех $x, y \in X$ , если $xRy$ и $yRx$ , то $x = y$ . Например, $\geq$ — антисимметричное отношение; то же самое и $>$ , но бессмысленно (условие в определении всегда ложно). ^[10]

Асимметричный: для всех $x, y \in X$ , если $xRy$ , то не $yRx$ . Отношение асимметрично тогда и только тогда, когда оно одновременно антисимметрично и иррефлексивно. ^[11] Например, $>$ является асимметричным отношением, а $\geq$ – нет.

Опять же, предыдущие три альтернативы далеко не исчерпывающие; Например, отношение $xRy$ , определяемое $x > 2,$ не является ни симметричным (например, $5 R 1$ , но не $1 R 5$ ), ни антисимметричным (например, $6 R 4$ , но также и $4 R 6$ ), не говоря уже о асимметричном.

Переходный: для всех $x, y, z \in X$ , если $xRy$ и $yRz$ , то $xRz$ . Транзитивное отношение иррефлексивно тогда и только тогда, когда оно асимметрично. ^[12] Например, «является предком» является транзитивным отношением, а «является родителем» — нет.

Связанный: для всех $x, y \in X$ , если $x \neq y$ , то $xRy$ или $yRx$ . Например, в натуральных числах $<$ связно, а " является делителем " - нет (например, ни $5 R 7$ , ни $7 R 5$ ).

Сильно связаны: для всех $x, y \in X$ , $xRy$ или $yRx$ . Например, в натуральных числах $\leq$ сильно связен, а $<$ нет. Отношение сильно связно тогда и только тогда, когда оно связно и рефлексивно.

Свойства уникальности:

инъективный ^[д] (также называемый уникальным слева ^[13]): Для всех $x, y, z \in X$ , если $xRy$ и $zRy$ , то $x = z$ . Например, зеленое и синее отношения на диаграмме являются инъективными, а красное - нет (поскольку оно связывает как $-1$ , так и $1$ с $1$ ), а также черное (поскольку оно связывает и $-1$ , и $1$ с $0$ ). .
Одновалентный ^[8]^[д] (также называемый уникальным по праву , ^[13] правоопределенный ^[14]): Для всех $x, y, z \in X$ , если $xRy$ и $xRz$ , то $y = z$ . Такое отношение называется частичной функцией . Например, красные и зеленые отношения на диаграмме являются функциональными, а синие — нет (поскольку они связывают $1$ как $с -1$ , так и $с 1$ ), а также не являются черными (поскольку они связывают 0 как с −1, так и с 1). .

Свойства совокупности:

Серийный ^[д] (также называемый общим или левым итогом ): Для всех $x \in X$ существует $такой y \in X$ , что $xRy$ . Такое отношение называется многозначной функцией . Например, красные и зеленые отношения на диаграмме являются полными, а синее — нет (поскольку оно не соотносит $-1$ с каким-либо действительным числом), а также не является черным (поскольку оно не соотносит $2$ ни с каким действительным числом). ). Другой пример: $>$ — это последовательное отношение к целым числам. нет $такого y$ Но это не серийное отношение к положительным целым числам, потому что среди положительных целых чисел $, что 1 > y$ . ^[15]Однако $<$ является последовательным отношением к положительным целым числам, рациональным числам и действительным числам. Каждое рефлексивное отношение является серийным: для данного $x$ выберите $y = x$ .

Сюръективный ^[д] (также называемый правом тоталом ^[13] или на ): Для всех $y \in Y$ существует $x \in X$ такой, что $xRy$ . Например, зеленое и синее отношения на диаграмме являются сюръективными, а красное — нет (поскольку оно не связывает ни одно действительное число с $-1$ ), а также черное (поскольку оно не связывает ни одно действительное число с $2).$ ).

Комбинации свойств [ править ]

Отношения по собственности
	Рефлексивность	Симметрия	Транзитивность	Связность	Пример
Частичный заказ	Рефл	Антисим	Да		Подмножество
Строгий частичный порядок	Иррефл	Асим	Да		Строгое подмножество
Общий заказ	Рефл	Антисим	Да	Да	Алфавитный порядок
Строгий общий порядок	Иррефл	Асим	Да	Да	Строгий алфавитный порядок
Отношение эквивалентности	Рефл	Сим	Да		Равенство

Отношения, которые удовлетворяют определенным комбинациям вышеперечисленных свойств, особенно полезны и поэтому получили собственные имена.

Отношение эквивалентности: Отношение, которое является рефлексивным, симметричным и транзитивным. Это также отношение симметричное, транзитивное и серийное, поскольку эти свойства предполагают рефлексивность.

Заказы:

Частичный заказ: Отношение, которое является рефлексивным, антисимметричным и транзитивным.

Строгий частичный порядок: Отношение, которое является иррефлексивным, асимметричным и транзитивным.

Общий заказ: Отношение рефлексивное, антисимметричное, транзитивное и связное. ^[16]

Строгий общий порядок: Отношение, которое является иррефлексивным, асимметричным, транзитивным и связным.

Свойства уникальности:

Один к одному ^[д]: Инъективный и одновалентный. Например, зеленое отношение на диаграмме взаимно однозначное, а красное, синее и черное — нет.
Один ко многим ^[д]: Инъективный и не однозначный. Например, синее отношение на диаграмме является отношением «один ко многим», а красное, зеленое и черное — нет.
Многие к одному ^[д]: Унивалентен и не инъективен. Например, красное отношение на диаграмме является отношением многие-к-одному, а зеленое, синее и черное — нет.
Многие ко многим ^[д]: Не инъективен и не однозначен. Например, черное отношение на диаграмме является отношением многие-ко-многим, а красное, зеленое и синее — нет.

Свойства уникальности и совокупности:

Функция ^[д]: Отношение одновалентное и тотальное. Например, красные и зеленые отношения на диаграмме являются функциями, а синие и черные — нет.
Инъекция ^[д]: Функция, которая является инъективной. Например, зеленое отношение на диаграмме является инъекцией, а красное, синее и черное — нет.
Сюръекция ^[д]: Функция, которая является сюръективной. Например, зеленое отношение на диаграмме является сюръекцией, а красное, синее и черное — нет.
Биекция ^[д]: Функция, которая является инъективной и сюръективной. Например, зеленое отношение на диаграмме является биекцией, а красное, синее и черное — нет.

Операции над отношениями [ править ]

Союз ^[Это]: Если $R$ и $S$ — отношения над $X$ , то $R \cup S знак равно { (Икс, y) | xRy или xSy}$ — объединения R $и$ S. $это$ отношение Элементом идентификации этой операции является пустое отношение. Например, $\leq$ — это объединение $<$ и $=$ , а $\geq$ — это объединение $>$ и $=$ .

Пересечение ^[Это]: Если $R$ и $S$ — отношения над $X,$ то $R \cap S знак равно { (x, y) | xRy и xSy}$ — пересечения R $и$ S. $это$ отношение Элементом идентичности этой операции является универсальное отношение. Например, «является младшей картой той же масти, что» является пересечением «является младшей картой, чем» и «принадлежит той же масти, что и».

Состав ^[Это]: Если $R$ и $S$ являются отношениями над $X,$ то $S \circ R знак равно { (Икс, z) | существует y \in X такой, что ySz} (также$ обозначаемый $R; S$ ) является относительным произведением R $xRy$ и $S.$ и Элементом идентичности является отношение идентичности. Порядок $R$ и $S$ в обозначениях $S \circ R$ , используемых здесь, соответствует стандартному порядку обозначений композиции функций . Например, композиция «является матерью» $\circ$ «является родителем» дает «является бабушкой и дедушкой по материнской линии», а композиция «является родителем» $\circ$ «является матерью» дает «является бабушкой». В первом случае, если $x$ является родителем $y$ , а $y$ является матерью $z$ , то $x$ является прародителем $z$ по материнской линии .

Конверсы ^[Это]: Если $R$ — отношение над множествами $X$ и $Y$ , то $R Т знак равно { (у, Икс) | xRy}$ — отношение R $Y$ над $X$ и $.$ обратное Например, $=$ является обратным самому себе, как и $\neq$ , а $<$ и $>$ являются обратными друг другу, как и $\leq$ и $\geq$ .

Дополнить ^[Это]: Если $R$ — отношение над $X,$ то $R знак равно { (x, y) | x, y \in X а не xRy}$ обозначаемый $R$ или $\negR,$ ) является отношением R. $дополнительным$ ( также Например, $=$ и $\neq$ являются дополнением друг друга, как и $\subseteq$ и $⊈$ , $\supseteq$ и $⊉$ , а также $\in$ и $\notin$ , а для полных порядков также $<$ и $\geq$ , и $>$ и $\leq$ . Дополнение обратного отношения $R Т$ является обратным дополнению: ${\overline {R^{\mathsf {T}}}}={\bar {R}}^{\mathsf {T}}.$

Ограничение ^[Это]: Если $R$ — отношение над $X$ , а $S$ — подмножество $X$ , то $R | S знак равно { (Икс, y) | xRy и x, y \in S}$ — это ограничения R $S$ к $.$ отношение Выражение $Р | S знак равно { (Икс, y) | xRy и x \in S}$ — это левоограниченное R $отношение$ к $S$ ; выражение $Р | С знак равно { (Икс, у) | xRy и y \in S}$ называется правоограниченное R $отношение$ к $S$ . Если отношение является рефлексивным , иррефлексивным, симметричным , антисимметричным , асимметричным , транзитивным , полным , трихотомическим , частичным порядком , полным порядком , строгим слабым порядком , полным предпорядком (слабый порядок) или отношением эквивалентности , то такими же являются и его ограничения. Однако транзитивное замыкание ограничения является подмножеством ограничения транзитивного замыкания, т. е., вообще говоря, не равно. Например, ограничение отношения « $x$ является родителем $y$ » женщинами приводит к отношению « $x$ — мать женщины $y$ »; его транзитивное замыкание не связывает женщину с ее бабушкой по отцовской линии. С другой стороны, транзитивное замыкание «является родителем» есть «является предком»; его ограничение на женщин действительно связывает женщину с ее бабушкой по отцовской линии.

Отношение $R$ над множествами $X$ и $Y$ называется содержится в отношении $S$ над $X$ и $Y$ , записанном $R \subseteq S$ , если $R$ является подмножеством $S$ , то есть для всех $x \in X$ и $y \in Y$ , если $xRy$ , то $xSy$ . Если $R$ содержится в $S$ , а $S$ содержится в $R$ , то $R$ и $S$ называются равными пишут $R = S.$ и Если $R$ содержится в $S$ , но $S$ не содержится в $R$ , то $R$ называется меньше чем $S$ , пишется $R ⊊ S.$ , Например, для рациональных чисел отношение $>$ меньше, чем $\geq$ , и равно композиции $> \circ >$ .

Теоремы об отношениях [ править ]

Отношение асимметрично тогда и только тогда, когда оно антисимметрично и иррефлексивно.
Транзитивное отношение иррефлексивно тогда и только тогда, когда оно асимметрично.
Отношение рефлексивно тогда и только тогда, когда его дополнение иррефлексивно.
Отношение сильно связно тогда и только тогда, когда оно связно и рефлексивно.
Отношение равно обратному тогда и только тогда, когда оно симметрично.
Отношение связно тогда и только тогда, когда его дополнение антисимметрично.
Отношение является сильно связным тогда и только тогда, когда его дополнение асимметрично. ^[17]
Если отношение R содержится в отношении S , то
- Если $R$ рефлексивно, связно, сильно связно, тотально слева или тотально справа, то то же самое относится и к $S$ .
- Если $S$ иррефлексивно, асимметрично, антисимметрично, уникально слева или уникально справа, то и $R$ таким же является .
Отношение является рефлексивным, иррефлексивным, симметричным, асимметричным, антисимметричным, связным, сильно связным и транзитивным, если обратное отношение соответственно.

Примеры [ править ]

Орденские отношения , в том числе строгие приказы :
- Больше чем
- Больше или равно
- Меньше, чем
- Меньше или равно
- Делит (равномерно)
- Подмножество
Отношения эквивалентности :
- Равенство
- Параллельно с (для аффинных пространств )
- Находится в биекции с
- изоморфный
Отношение толерантности — рефлексивное и симметричное отношение:
- Отношение зависимости , конечное отношение допуска.
- Отношение независимости — дополнение к некоторому отношению зависимости.
Родственные отношения

Обобщения [ править ]

Вышеупомянутая концепция отношения была обобщена, чтобы допустить отношения между членами двух разных множеств. Учитывая множества $X$ и $Y$ , гетерогенное отношение $R$ над $X$ и $Y$ является подмножеством ${ (x, y) | Икс € Икс, Y у €}$ . ^[1]^[18]Когда $X = Y$ , получается описанная выше концепция отношения; его часто называют гомогенным отношением (или эндореляцией ) ^[19]^[20]отличить его от его обобщения. Вышеупомянутые свойства и операции, отмеченные " ^[д]" и " ^[Это]", соответственно, обобщают на гетерогенные отношения. Примером гетерогенного отношения является «океан $x$ граничит с континентом $y$ ». Наиболее известными примерами являются функции ^[ф] с отдельными доменами и диапазонами, например $sqrt : N \to R +$ .

См. также [ править ]

Структура инцидентности , неоднородное отношение между набором точек и линий.
Теория порядка исследует свойства отношений порядка.

Примечания [ править ]

^ называется «однородным бинарным отношением (на множествах)», когда важно разграничение его обобщений
^ обобщение множеств
^ см . ниже
^ Перейти обратно: ^а ^б ^с ^д ^Это ^ж ^г ^час ^я ^дж ^к ^л ^м Эти свойства также распространяются на гетерогенные отношения.
^ Перейти обратно: ^а ^б ^с ^д ^Это ^ж ^г Эта операция также обобщается на гетерогенные отношения.
^ то есть уникальные справа и гетерогенные отношения слева

Ссылки [ править ]

^ Перейти обратно: ^а ^б ^с Кодд 1970 г.
^ Халмос 1968 , Глава 14
^ Халмош 1968 , Глава 7
^ «Определение отношения – Math Insight» . mathinsight.org . Проверено 11 декабря 2019 г.
^ Халмос 1968 , Глава 8
^ Перейти обратно: ^а ^б Эрнст Шредер (1895) Алгебра и логика родственников , через Интернет-архив
^ Перейти обратно: ^а ^б К.И. Льюис (1918) Обзор символической логики , стр. 269–279, через интернет-архив.
^ Перейти обратно: ^а ^б Шмидт 2010 , гл. 5
^ Эндертон 1977 , глава 3. с. 40
^ Смит, Эгген и Сент-Андре 2006 , стр. 160.
^ Нивергельт 2002 , с. 158
^ Флашка и др. 2007 , стр.1 Лемма 1.1 (iv). Этот источник называет асимметричные отношения «строго антисимметричными».
^ Перейти обратно: ^а ^б ^с Килп, Кнауэр и Михалев 2000 , с. 3. Те же четыре определения встречаются ниже: Pahl & Damrath 2001 , p. 506, Бест 1996 , стр. 101-1. . 19–21, Риман стр . 21–22
^ Мас 2007
^ Яо и Вонг 1995
^ Розенштейн 1982 , с. 4
^ Шмидт и Стрёлейн, 1993 г.
^ Эндертон 1977 , глава 3. с. 40
^ Мюллер 2012 , с. 22
^ Пал и Дамрат 2001 , с. 496

Библиография [ править ]

Лучший, Эйке (1996). Семантика последовательных и параллельных программ . Прентис Холл. ISBN 978-0-13-460643-9 .
Кодд, Эдгар Франк (июнь 1970 г.). «Реляционная модель данных для больших общих банков данных» (PDF) . Коммуникации АКМ . 13 (6): 377–387. дои : 10.1145/362384.362685 . S2CID 207549016 . Проверено 29 апреля 2020 г.
Кодд, Эдгар Франк (1990). Реляционная модель управления базами данных: версия 2 (PDF) . Бостон: Аддисон-Уэсли . ISBN 978-0201141924 .
Эндертон, Герберт (1977). Элементы теории множеств . Бостон: Академическая пресса . ISBN 978-0-12-238440-0 .
Флашка, В.; Ежек, Дж.; Кепка, Т.; Кортелайнен, Дж. (2007). Транзитивные замыкания бинарных отношений I (PDF) . Прага: Школа математики – Физика Карлова университета. Архивировано из оригинала (PDF) 2 ноября 2013 г.
Халмос, Пол Р. (1968). Наивная теория множеств . Принстон: Ностранд.
Килп, Мати; Кнауэр, Ульрих; Михалев, Александр (2000). Моноиды, акты и категории: с приложениями к сплетенным произведениям и графам . Берлин: Де Грюйтер . ISBN 978-3-11-015248-7 .
Мэс, Стефан (2007), «Рассуждения об ограничениях пространственной семантической целостности», Теория пространственной информации: 8-я Международная конференция, COSIT 2007, Мельбурн, Австралия, 19–23 сентября, Труды , Конспекты лекций по информатике, том. 4736, Springer, стр. 285–302, номер документа : 10.1007/978-3-540-74788-8_18.
Мюллер, Мэн (2012). Открытие реляционных знаний . Издательство Кембриджского университета. ISBN 978-0-521-19021-3 .
Нивергельт, Ив (2002), Основы логики и математики: приложения к информатике и криптографии , Springer-Verlag
Паль, Питер Дж.; Дамрат, Рудольф (2001). Математические основы вычислительной техники: Справочник . Springer Science & Business Media. ISBN 978-3-540-67995-0 .
Пирс, Чарльз Сандерс (1873). «Описание обозначений логики родственников, возникающее в результате расширения представлений о логическом исчислении Буля» . Мемуары Американской академии искусств и наук . 9 (2): 317–178. Бибкод : 1873MAAAS...9..317P . дои : 10.2307/25058006 . hdl : 2027/hvd.32044019561034 . JSTOR 25058006 . Проверено 5 мая 2020 г.
Риман, Роберт-Кристоф (1999). Моделирование параллельных систем: структурные и семантические методы в исчислении сетей Петри высокого уровня . Герберт Утц Верлаг. ISBN 978-3-89675-629-9 .
Розенштейн, Джозеф Г. (1982), Линейные порядки , Academic Press, ISBN 0-12-597680-1
Шмидт, Гюнтер (2010). Реляционная математика . Кембридж: Издательство Кембриджского университета . ISBN 978-0-521-76268-7 .
Шмидт, Гюнтер ; Стрёлейн, Томас (1993). Отношения и графики: дискретная математика для компьютерщиков . Берлин: Шпрингер. ISBN 978-3-642-77970-1 .
Смит, Дуглас; Эгген, Морис; Сент-Андре, Ричард (2006), Переход к высшей математике (6-е изд.), Брукс/Коул, ISBN 0-534-39900-2
Яо, ГГ; Вонг, СКМ (1995). «Обобщение грубых наборов с использованием связей между значениями атрибутов» (PDF) . Материалы 2-й ежегодной совместной конференции по информационным наукам : 30–33.

[9] называется «однородным бинарным отношением (на множествах)», когда важно разграничение его обобщений

[10] обобщение множеств

[12] см . ниже

[heterogeneous-16] Перейти обратно: ^а ^б ^с ^д ^Это ^ж ^г ^час ^я ^дж ^к ^л ^м Эти свойства также распространяются на гетерогенные отношения.

[heterogeneous_operation-21] Перейти обратно: ^а ^б ^с ^д ^Это ^ж ^г Эта операция также обобщается на гетерогенные отношения.

[26] то есть уникальные справа и гетерогенные отношения слева

[FOOTNOTECodd1970-1] Перейти обратно: ^а ^б ^с Кодд 1970 г.

[FOOTNOTEHalmos1968Ch_14-2] Халмос 1968 , Глава 14

[FOOTNOTEHalmos1968Ch_7-3] Халмош 1968 , Глава 7

[4] «Определение отношения – Math Insight» . mathinsight.org . Проверено 11 декабря 2019 г.

[FOOTNOTEHalmos1968Ch_8-5] Халмос 1968 , Глава 8

[Schroder.1895-6] Перейти обратно: ^а ^б Эрнст Шредер (1895) Алгебра и логика родственников , через Интернет-архив

[Lewis.1918-7] Перейти обратно: ^а ^б К.И. Льюис (1918) Обзор символической логики , стр. 269–279, через интернет-архив.

[FOOTNOTESchmidt2010Chapt._5-8] Перейти обратно: ^а ^б Шмидт 2010 , гл. 5

[FOOTNOTEEnderton1977Ch_3._p._40-11] Эндертон 1977 , глава 3. с. 40

[FOOTNOTESmithEggenSt._Andre2006160-13] Смит, Эгген и Сент-Андре 2006 , стр. 160.

[FOOTNOTENievergelt2002[httpsbooksgooglecombooksid_H_nJdagqL8CpgPA158_158]-14] Нивергельт 2002 , с. 158

[FOOTNOTEFlaškaJežekKepkaKortelainen2007p.1_Lemma_1.1_(iv)._This_source_refers_to_asymmetric_relations_as_"strictly_antisymmetric".-15] Флашка и др. 2007 , стр.1 Лемма 1.1 (iv). Этот источник называет асимметричные отношения «строго антисимметричными».

[kkm-17] Перейти обратно: ^а ^б ^с Килп, Кнауэр и Михалев 2000 , с. 3. Те же четыре определения встречаются ниже: Pahl & Damrath 2001 , p. 506, Бест 1996 , стр. 101-1. . 19–21, Риман стр . 21–22

[FOOTNOTEMäs2007-18] Мас 2007

[FOOTNOTEYaoWong1995-19] Яо и Вонг 1995

[FOOTNOTERosenstein19824-20] Розенштейн 1982 , с. 4

[FOOTNOTESchmidtStröhlein1993-22] Шмидт и Стрёлейн, 1993 г.

[23] Эндертон 1977 , глава 3. с. 40

[FOOTNOTEMüller201222-24] Мюллер 2012 , с. 22

[FOOTNOTEPahlDamrath2001496-25] Пал и Дамрат 2001 , с. 496

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[а]

[б]

[9]

[с]

[10]

[11]

[12]

[д]

[13]

[14]

[15]

[16]

[Это]

[17]

[18]

[19]

[20]

[ф]