Диаграмма Хассе

В теории порядка диаграмма Хассе ( / ˈ h æ s ə / ; Немецкий: [ˈhasə] ) — тип математической диаграммы , используемой для представления конечного частично упорядоченного множества , в виде рисунка его транзитивной редукции . Конкретно, для частично упорядоченного множества $(S,\leq )$ один представляет каждый элемент $S$ как вершина на плоскости и рисует отрезок линии или кривую, идущую вверх от одной вершины $x$ в другую вершину $y$ в любое время $y$ крышки $x$ (то есть всякий раз, когда $x\neq y$ , $x\leq y$ и нет $z$ в отличие от $x$ и $y$ с $x\leq z\leq y$ ). Эти кривые могут пересекать друг друга, но не должны касаться каких-либо вершин, кроме своих конечных точек. Такая диаграмма с помеченными вершинами однозначно определяет ее частичный порядок.

Диаграммы Хассе названы в честь Гельмута Хассе (1898–1979); по словам Гаррета Биркгоффа , они названы так из-за эффективного использования их Хассе. ^[1]Однако Хассе был не первым, кто использовал эти диаграммы. Один из примеров, предшествовавших Хассе, можно найти в работе Анри Гюстава Фогта 1895 года. ^[2]^[3] Хотя диаграммы Хассе изначально были разработаны как метод рисования частично упорядоченных множеств вручную, в последнее время они создаются автоматически с использованием методов рисования графов . ^[4]

В некоторых источниках словосочетание «диаграмма Хассе» имеет другое значение: ориентированный ациклический граф , полученный из отношения покрытия частично упорядоченного множества, независимо от какого-либо изображения этого графа. ^[5]

Дизайн диаграммы [ править ]

Хотя диаграммы Хассе являются простыми и интуитивно понятными инструментами для работы с конечными частично упорядоченными множествами , нарисовать «хорошие» диаграммы оказывается довольно сложно. Причина в том, что, как правило, существует множество различных способов построения диаграммы Хассе для данного ЧУ-множества. Простой метод, заключающийся в том, что мы начинаем с минимальных элементов порядка, а затем постепенно рисуем более крупные элементы, часто дает весьма плохие результаты: симметрия и внутренняя структура порядка легко теряются.

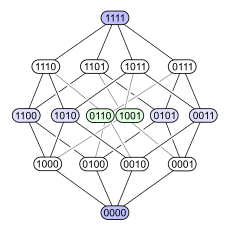
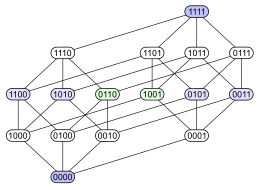
Следующий пример демонстрирует проблему. Рассмотрим степенной набор 4-элементного множества, упорядоченного по включению $\subseteq$ . Ниже приведены четыре различные диаграммы Хассе для этого частичного порядка. Каждое подмножество имеет узел, помеченный двоичной кодировкой, которая показывает, входит ли определенный элемент в подмножество (1) или нет (0):

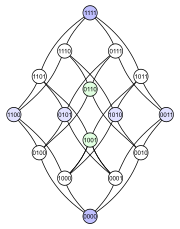Первая диаграмма ясно показывает, что набор степеней является градуированным ЧУМ . Вторая диаграмма имеет такую же градуированную структуру, но, делая некоторые ребра длиннее других, она подчеркивает, что 4-мерный куб представляет собой комбинаторное объединение двух 3-мерных кубов, и что тетраэдр ( абстрактный 3-мерный многогранник ) аналогичным образом объединяет два треугольники ( абстрактные 2-многогранники ). Третья диаграмма демонстрирует некоторую внутреннюю симметрию конструкции. На четвертой диаграмме вершины расположены в сетке 4×4.

Восходящая планарность [ править ]

Если частичный порядок можно изобразить в виде диаграммы Хассе, в которой никакие два ребра не пересекаются, то его граф покрытия называется плоскостью вверх . Известен ряд результатов о восходящей планарности и построении беспересекающихся диаграмм Хассе:

Если рисуемый частичный порядок представляет собой решетку , то его можно нарисовать без пересечений тогда и только тогда, когда его размерность порядка не превышает двух. ^[6] В этом случае непересекающийся рисунок можно найти, выведя декартовы координаты элементов из их положений в двух линейных порядках, реализующих размерность порядка, а затем повернув рисунок против часовой стрелки на угол 45 градусов.
Если частичный порядок имеет не более одного минимального элемента или не более одного максимального элемента , то можно за линейное время проверить , имеет ли он непересекающуюся диаграмму Хассе. ^[7]
NP -полно, чтобы определить, можно ли изобразить частичный порядок с несколькими источниками и стоками в виде диаграммы Хассе без пересечений. ^[8] Однако найти диаграмму Хассе без пересечений можно с помощью фиксированного параметра, если она параметризована количеством точек сочленения и трехсвязных компонентов транзитивной редукции частичного порядка. ^[9]
Если указаны координаты y элементов частичного порядка, то диаграмма Хассе без пересечений, учитывающая эти назначения координат, может быть найдена за линейное время, если такая диаграмма существует. ^[10] В частности, если входное ЧУУ является градуированным ЧУУ , можно за линейное время определить, существует ли диаграмма Хассе без пересечений, в которой высота каждой вершины пропорциональна ее рангу.

Использование в нотации UML [ править ]

В программной инженерии / объектно-ориентированном проектировании классы . программной системы и отношения наследования между этими классами часто изображаются с помощью диаграммы классов , формы диаграммы Хассе, в которой ребра, соединяющие классы, рисуются в виде сегментов сплошной линии с открытым пространством треугольник в конце суперкласса.

Примечания [ править ]

^ Биркгоф (1948) .
^ Фогт (1895) .
^ Соперник (1985) , с. 110.
^ Например, см. Ди Баттиста и Тамассия (1988) и Фриз (2004) .
^ Примеры этого альтернативного значения диаграмм Хассе см. в Christofides (1975 , стр. 170–174); Туласираман и Свами (1992) ; Банг-Дженсен (2008)
^ Гарг и Тамассия (1995a) , Теорема 9, с. 118; Бейкер, Фишберн и Робертс (1971) , Теорема 4.1, с.
^ Гарг и Тамассия (1995a) , Теорема 15, с. 125; Бертолацци и др. (1993 )
^ Гарг и Тамассия (1995a) , Следствие 1, с. 132; Гарг и Тамассия (1995b) .
^ Чан (2004) .
^ Юнгер и Лейперт (1999) .

Ссылки [ править ]

Бейкер, Кирби А.; Фишберн, Питер С .; Робертс, Фред С. (1971), «Частичные порядки размерности 2», Networks , 2 (1): 11–28, doi : 10.1002/net.3230020103
Банг-Йенсен, Йорген (2008), «2.1 Ациклические орграфы», Орграфы: теория, алгоритмы и приложения , Монографии Springer по математике (2-е изд.), Springer-Verlag, стр. 32–34, ISBN 978-1-84800-997-4
Бертолацци, Р; Баттиста, Г.; Маннино, К.; Тамассиа, Р. (1993), «Оптимальное тестирование восходящей планарности орграфов с одним источником» (PDF) , Proc. 1-й Европейский симпозиум по алгоритмам (ESA '93) , Конспекты лекций по информатике , том. 726, Springer-Publishers, стр. 101–1. 37–48, CiteSeerX 10.1.1.43.4879 , doi : 10.1007/3-540-57273-2_42 , ISBN 978-3-540-57273-2
Биркгоф, Гаррет (1948), Теория решетки (пересмотренная редакция), Американское математическое общество
Чан, Хьюберт (2004), «Параметризованный алгоритм проверки восходящей планарности», Proc. 12-й Европейский симпозиум по алгоритмам (ESA '04) , Конспекты лекций по информатике, том. 3221, Springer-Verlag, стр. 157–168, номер документа : 10.1007/978-3-540-30140-0_16.
Кристофидес, Никос (1975), Теория графов: алгоритмический подход , Academic Press, стр. 170–174.
Ди Баттиста, Г.; Тамассиа, Р. (1988), «Алгоритмы плоского представления ациклических орграфов», Theoretical Computer Science , 61 (2–3): 175–178, doi : 10.1016/0304-3975(88)90123-5
Фриз, Ральф (2004), «Автоматическое рисование решетки», Concept Lattices (PDF) , Конспекты лекций по информатике, том. 2961, Springer-Verlag, стр. 589–590.
Гарг, Ашим; Тамассия, Роберто (1995a), «Тестирование восходящей планарности», Order , 12 (2): 109–133, doi : 10.1007/BF01108622 , S2CID 14183717
Гарг, Ашим; Тамассиа, Роберто (1995b), «О вычислительной сложности тестирования восходящей и прямолинейной планарности», Рисование графика (Proc. GD '94) , LectureNotes in Computer Science, vol. 894, Springer-Verlag, стр. 286–297, номер документа : 10.1007/3-540-58950-3_384 , ISBN. 978-3-540-58950-1
Юнгер, Майкл; Лейперт, Себастьян (1999), «Вложение уровней плоскостей в линейное время», Рисование графиков (Proc. GD '99) , Конспекты лекций по информатике, том. 1731, стр. 72–81, номер документа : 10.1007/3-540-46648-7_7 , ISBN. 978-3-540-66904-3
Ривал, Иван (1985), «Диаграмма», в книге Ривал, Иван (ред.), Графы и порядок: роль графов в теории упорядоченных множеств и ее приложениях, Труды Института перспективных исследований НАТО, проводимые в Банфе, 18–31 мая 1984 г. , Серия C Институтов передовых научных исследований НАТО: Математические и физические науки, том. 147, Райдель, Дордрехт, стр. 103–133, MR 0818494
Туласираман, К.; Свами, MNS (1992), «5.7 Ациклические ориентированные графы», Графы: теория и алгоритмы , Джон Вили и сын, стр. 118, ISBN 978-0-471-51356-8
Фогт, Анри Гюстав (1895), Уроки алгебраического решения уравнений , Нони, с. 91

Внешние ссылки [ править ]

Соответствующие СМИ на Wikimedia Commons:
- Диаграмма Хассе (Галерея)
- Диаграммы Хассе (Категория)
Вайсштейн, Эрик В. , «Диаграмма Хассе» , MathWorld

[FOOTNOTEBirkhoff1948-1] Биркгоф (1948) .

[FOOTNOTEVogt1895-2] Фогт (1895) .

[FOOTNOTERival1985110-3] Соперник (1985) , с. 110.

[4] Например, см. Ди Баттиста и Тамассия (1988) и Фриз (2004) .

[5] Примеры этого альтернативного значения диаграмм Хассе см. в Christofides (1975 , стр. 170–174); Туласираман и Свами (1992) ; Банг-Дженсен (2008)

[6] Гарг и Тамассия (1995a) , Теорема 9, с. 118; Бейкер, Фишберн и Робертс (1971) , Теорема 4.1, с.

[7] Гарг и Тамассия (1995a) , Теорема 15, с. 125; Бертолацци и др. (1993 )

[8] Гарг и Тамассия (1995a) , Следствие 1, с. 132; Гарг и Тамассия (1995b) .

[FOOTNOTEChan2004-9] Чан (2004) .

[FOOTNOTEJüngerLeipert1999-10] Юнгер и Лейперт (1999) .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

v т Это Теория порядка
Topics Glossary Category
Key concepts	Binary relation Boolean algebra Cyclic order Lattice Partial order Preorder Total order Weak ordering
Results	Boolean prime ideal theorem Cantor–Bernstein theorem Cantor's isomorphism theorem Dilworth's theorem Dushnik–Miller theorem Hausdorff maximal principle Knaster–Tarski theorem Kruskal's tree theorem Laver's theorem Mirsky's theorem Szpilrajn extension theorem Zorn's lemma
Properties & Types (list)	Antisymmetric Asymmetric Boolean algebra topics Completeness Connected Covering Dense Directed (Partial) Equivalence Foundational Heyting algebra Homogeneous Idempotent Lattice Bounded Complemented Complete Distributive Join and meet Reflexive Partial order Chain-complete Graded Eulerian Strict Prefix order Preorder Total Semilattice Semiorder Symmetric Total Tolerance Transitive Well-founded Well-quasi-ordering (Better) (Pre) Well-order
Constructions	Composition Converse/Transpose Lexicographic order Linear extension Product order Reflexive closure Series-parallel partial order Star product Symmetric closure Transitive closure
Topology & Orders	Alexandrov topology & Specialization preorder Ordered topological vector space Normal cone Order topology Order topology Topological vector lattice Banach Fréchet Locally convex Normed
Related	Antichain Cofinal Cofinality Comparability Graph Duality Filter Hasse diagram Ideal Net Subnet Order morphism Embedding Isomorphism Order type Ordered field Positive cone of an ordered field Ordered vector space Partially ordered Positive cone of an ordered vector space Riesz space Partially ordered group Positive cone of a partially ordered group Upper set Young's lattice