Решетка подгрупп

В математике решетка подгрупп группы $G$ — решетка которой являются подгруппы , элементами $G$ , при этом частичный порядок устанавливается включением .В этой решетке соединение двух подгрупп — это подгруппа, порожденная их объединением , а встреча двух подгрупп — это их пересечение .

Пример [ править ]

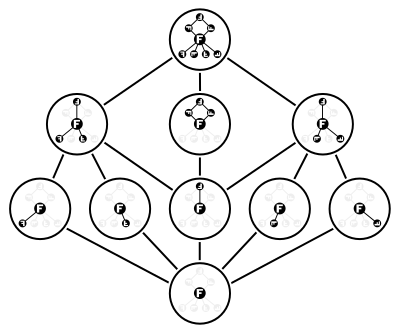
Группа диэдра Dih ₄ имеет десять подгрупп, считая себя и тривиальную подгруппу. Пять из восьми элементов группы порождают подгруппы второго порядка , а два других нетождественных элемента порождают одну и ту же циклическую подгруппу четвертого порядка. Кроме того, существуют две подгруппы вида Z ₂ × Z ₂ , порожденные парами элементов порядка -два . Решетка, образованная этими десятью подгруппами, показана на иллюстрации.

Этот пример также показывает, что решетка всех подгрупп группы не является модулярной решеткой вообще запрещенный «пятиугольник» N ₅ . Действительно, именно эта решетка содержит в качестве подрешетки .

Свойства [ править ]

Для любых подгрупп A , B и C группы с A ⩽ C ( A подгруппа C ), то AB ∩ C = A ( B ∩ C ); умножение здесь есть произведение подгрупп . Это свойство было названо модульным свойством групп ( Ашбахер 2000 ) или ( Дедекинда модульным законом ) ( Робинсон 1996 , Кон 2000 ). Поскольку для двух нормальных подгрупп произведение фактически является наименьшей подгруппой, содержащей эти две, нормальные подгруппы образуют модулярную решетку .

Теорема о решетке устанавливает связь Галуа между решеткой подгрупп группы и решеткой ее частных .

Лемма Цассенхауза дает изоморфизм между некоторыми комбинациями факторов и произведений в решетке подгрупп.

В общем случае нет ограничений на форму решетки подгрупп в том смысле, что каждая решетка изоморфна подрешетке решетки подгрупп некоторой группы. Более того, каждая конечная решетка изоморфна подрешетке решетки подгрупп некоторой конечной группы ( Шмидт 1994 , стр. 9). Любая конечная дистрибутивная решетка также изоморфна решетке нормальных подгрупп некоторой группы ( Силкок, 1977 ).

Характеристические решетки [ править ]

Подгруппы с определенными свойствами образуют решетки, а другие свойства — нет.

Нормальные подгруппы всегда образуют модулярную решетку . Фактически, существенное свойство, гарантирующее модулярность решетки, состоит в том, что подгруппы коммутируют друг с другом, т. е. являются квазинормальными подгруппами .
Нильпотентные нормальные подгруппы образуют решетку, которая является (частью) содержанием теоремы Фиттинга .
Класс групп называется классом Фиттинга, если он замкнут относительно изоморфизма, субнормальных подгрупп и произведений субнормальных подгрупп. Для любого класса Фиттинга F как субнормальные F -подгруппы, так и нормальные F -подгруппы образуют решетки. Это обобщает вышеизложенное на F — класс нильпотентных групп, а другим примером является F — класс разрешимых групп .
Центральные подгруппы образуют решетку.

Однако ни конечные подгруппы, ни периодические подгруппы не образуют решетку: например, свободное произведение $\mathbf {Z} /2\mathbf {Z} *\mathbf {Z} /2\mathbf {Z}$ порождается двумя элементами кручения , но бесконечна и содержит элементы бесконечного порядка.

Тот факт, что нормальные подгруппы образуют модулярную решетку, является частным случаем более общего результата, а именно того, что в любом многообразии Мальцева (примером которого являются группы) решетка конгруэнций является модулярной ( Kearnes & Kiss 2013 ).

Характеристика групп по решеткам их подгрупп [ править ]

Теоретико-решеточная информация о решетке подгрупп иногда может использоваться для вывода информации об исходной группе - идея, восходящая к работам Ойстейна Оре ( 1937 , 1938 ). Например, как доказал Оре , группа локально циклична тогда и только тогда, когда ее решетка подгрупп дистрибутивна . Если дополнительно решетка удовлетворяет условию возрастающей цепи , то группа циклическая.

Группы, решетка подгрупп которых является дополняемой решеткой, называются дополненными группами ( Захер, 1953 ), а группы, решетка подгрупп которых является модулярной решеткой, называются группами Ивасавы или модулярными группами ( Ивасава, 1941 ). Теоретико-решеточные характеристики этого типа существуют также для разрешимых и совершенных групп ( Сузуки, 1951 ).

Ссылки [ править ]

Ашбахер, М. (2000). Теория конечных групп . Издательство Кембриджского университета. п. 6. ISBN 978-0-521-78675-1 .
Баер, Рейнхольд (1939). «Значение системы подгрупп для строения группы». Американский журнал математики . 61 (1). Издательство Университета Джонса Хопкинса: 1–44. дои : 10.2307/2371383 . JSTOR 2371383 .
Кон, Пол Мориц (2000). Классическая алгебра . Уайли. п. 248. ИСБН 978-0-471-87731-8 .
Ивасава, Кенкити (1941), «О конечных группах и ассоциациях их подгрупп», J. Fac. наук. Имп. Токио. Секта. И. , 4 : 171–199, МР 0005721
Кирнс, Кейт; Поцелуй, Эмиль В. (2013). Форма конгруэнтных решеток . Американское математическое соц. п. 3. ISBN 978-0-8218-8323-5 .
Оре, Эйстейн (1937). «Структуры и теория групп. I». Математический журнал Дьюка . 3 (2): 149–174. дои : 10.1215/S0012-7094-37-00311-9 . МР 1545977 .
Оре, Эйстейн (1938). «Структуры и теория групп. II». Математический журнал Дьюка . 4 (2): 247–269. дои : 10.1215/S0012-7094-38-00419-3 . hdl : 10338.dmlcz/100155 . МР 1546048 .
Робинсон, Дерек (1996). Курс теории групп . Springer Science & Business Media. п. 15. ISBN 978-0-387-94461-6 .
Роттлендер, Ада (1928). «Доказательство существования неизоморфных групп равного положения подгрупп». Математический журнал . 28 (1): 641–653. дои : 10.1007/BF01181188 . S2CID 120596994 .
Шмидт, Роланд (1994). Решетки подгрупп групп . Выставки по математике. Том. 14. Вальтер де Грюйтер. ISBN 978-3-11-011213-9 . Обзор Ральфа Фриза в Bull. AMS 33 (4): 487–492.
Сузуки, Мичио (1951). «О решетке подгрупп конечных групп» . Труды Американского математического общества . 70 (2). Американское математическое общество: 345–371. дои : 10.2307/1990375 . JSTOR 1990375 .
Сузуки, Мичио (1956). Структура группы и структура ее решетки подгрупп . Берлин: Springer Verlag.
Яковлев, Б.В. (1974). «Условия, при которых решетка изоморфна решетке подгрупп группы». Алгебра и логика . 13 (6): 400–412. дои : 10.1007/BF01462952 . S2CID 119943975 .
Силкок, Ховард Л. (1977). «Обобщенное сплетение и решетка нормальных подгрупп группы» (PDF) . Алгебра Универсалис . 7 : 361–372.
Захер, Джон (1953). «Характеризация дополняемых разрешимых групп конечного порядка» . Отчеты математического семинара Падуанского университета . 22 : 113–122. ISSN 0041-8994 . МР 0057878 .

Внешние ссылки [ править ]