Решетка (заказать)

Не путать с Решёткой (группой) .

showТранзитивные   бинарные отношения
Symmetric Antisymmetric Connected Well-founded Has joins Has meets Reflexive Irreflexive Asymmetric Total, Semiconnex Anti- reflexive Equivalence relation Y ✗ ✗ ✗ ✗ ✗ Y ✗ ✗ Preorder (Quasiorder) ✗ ✗ ✗ ✗ ✗ ✗ Y ✗ ✗ Partial order ✗ Y ✗ ✗ ✗ ✗ Y ✗ ✗ Total preorder ✗ ✗ Y ✗ ✗ ✗ Y ✗ ✗ Total order ✗ Y Y ✗ ✗ ✗ Y ✗ ✗ Prewellordering ✗ ✗ Y Y ✗ ✗ Y ✗ ✗ Well-quasi-ordering ✗ ✗ ✗ Y ✗ ✗ Y ✗ ✗ Well-ordering ✗ Y Y Y ✗ ✗ Y ✗ ✗ Lattice ✗ Y ✗ ✗ Y Y Y ✗ ✗ Join-semilattice ✗ Y ✗ ✗ Y ✗ Y ✗ ✗ Meet-semilattice ✗ Y ✗ ✗ ✗ Y Y ✗ ✗ Strict partial order ✗ Y ✗ ✗ ✗ ✗ ✗ Y Y Strict weak order ✗ Y ✗ ✗ ✗ ✗ ✗ Y Y Strict total order ✗ Y Y ✗ ✗ ✗ ✗ Y Y Symmetric Antisymmetric Connected Well-founded Has joins Has meets Reflexive Irreflexive Asymmetric Definitions, for all $a,b$ and $S\neq \varnothing :$ ${\begin{aligned}&aRb\\\Rightarrow {}&bRa\end{aligned}}$ ${\begin{aligned}aRb{\text{ and }}&bRa\\\Rightarrow a={}&b\end{aligned}}$ ${\begin{aligned}a\neq {}&b\Rightarrow \\aRb{\text{ or }}&bRa\end{aligned}}$ ${\begin{aligned}\min S\\{\text{exists}}\end{aligned}}$ ${\begin{aligned}a\vee b\\{\text{exists}}\end{aligned}}$ ${\begin{aligned}a\wedge b\\{\text{exists}}\end{aligned}}$ $aRa$ ${\text{not }}aRa$ ${\begin{aligned}aRb\Rightarrow \\{\text{not }}bRa\end{aligned}}$
Y indicates that the column's property is always true the row's term (at the very left), while ✗ indicates that the property is not guaranteed in general (it might, or might not, hold). For example, that every equivalence relation is symmetric, but not necessarily antisymmetric, is indicated by Y in the "Symmetric" column and ✗ in the "Antisymmetric" column, respectively. All definitions tacitly require the homogeneous relation $R$ be transitive: for all $a,b,c,$ if $aRb$ and $bRc$ then $aRc.$ A term's definition may require additional properties that are not listed in this table.

Решетка математических — абстрактная структура, изучаемая в разделах теории порядка и абстрактной алгебры . Он состоит из частично упорядоченного набора , в котором каждая пара элементов имеет уникальную верхнюю границу (также называемую наименьшей верхней границей или соединением ) и уникальную нижнюю границу (также называемую наибольшей нижней границей или пересечением ). Примером может служить набор степеней множества, частично упорядоченного по включению , для которого верхняя грань — это объединение , а нижняя грань — пересечение . Другой пример - натуральные числа , частично упорядоченные по делимости , для которых верхняя грань является наименьшим общим кратным , а нижняя грань - наибольшим общим делителем .

Решетки также можно охарактеризовать как алгебраические структуры, удовлетворяющие определенным аксиоматическим тождествам . Поскольку эти два определения эквивалентны, теория решеток опирается как на теорию порядка, так и на универсальную алгебру . Полурешетки включают решетки, которые, в свою очередь, включают в себя гейтингову и булеву алгебры . Все эти решетчатые структуры допускают как теоретико-порядковое, так и алгебраическое описание.

Подобласть абстрактной алгебры , изучающая решетки, называется теорией решеток .

Определение

Решетку можно определить либо с точки зрения теории порядка, как частично упорядоченное множество, либо как алгебраическую структуру.

Как частично заказанный набор

( Частично упорядоченный набор poset) $(L,\leq )$ называется решеткой , если она является одновременно объединенной и полурешеткой , т. е. каждое двухэлементное подмножество $\{a,b\}\subseteq L$ имеет соединение (т.е. наименьшую верхнюю границу, обозначаемую $a\vee b$) и двойственное соответствие (т.е. величайшая нижняя граница , обозначаемая $a\wedge b$). Это определение делает $\,\wedge \,$ и $\,\vee \,$ бинарные операции . Обе операции монотонны относительно заданного порядка: $a_{1}\leq a_{2}$ и $b_{1}\leq b_{2}$ подразумевает, что $a_{1}\vee b_{1}\leq a_{2}\vee b_{2}$ и $a_{1}\wedge b_{1}\leq a_{2}\wedge b_{2}.$

следует По индукции , что каждое непустое конечное подмножество решетки имеет наименьшую верхнюю и наибольшую нижнюю границы. При дополнительных предположениях могут быть возможны дальнейшие выводы; см. Полноту (теорию порядка) для получения дополнительной информации по этому вопросу. В этой статье также обсуждается, как можно перефразировать приведенное выше определение с точки зрения существования подходящих связей Галуа между связанными частично упорядоченными множествами - подход, представляющий особый интерес для теоретико-категорного подхода к решеткам и для анализа формальных концепций .

Учитывая подмножество решетки, $H\subseteq L,$ встречи и соединения ограничиваются частичными функциями – они не определены, если их значение не находится в подмножестве $H.$ Полученная структура на $H$ называется частичная решетка . В дополнение к этому внешнему определению как подмножеству некоторой другой алгебраической структуры (решетки), частичная решетка также может быть внутренне определена как набор с двумя частичными бинарными операциями, удовлетворяющими определенным аксиомам.

Как алгебраическая структура

Решетка — это алгебраическая структура $(L,\vee ,\wedge )$, состоящий из набора $L$ и две бинарные, коммутативные и ассоциативные операции $\vee$ и $\wedge$ на $L$ удовлетворяющие следующим аксиоматическим тождествам для всех элементов $a,b\in L$ (иногда называемые законами поглощения ):

$$a\vee (a\wedge b)=a$$

$$a\wedge (a\vee b)=a$$

Следующие два тождества также обычно считаются аксиомами, хотя они и следуют из двух законов поглощения, взятых вместе. Это так называемые идемпотентные законы .

$$a\vee a=a$$

$$a\wedge a=a$$

Эти аксиомы утверждают, что обе $(L,\vee )$ и $(L,\wedge )$ являются полурешетками . Законы поглощения, единственные вышеприведенные аксиомы, в которых фигурируют и встречаются, и соединяются, отличают решетку от произвольной пары полурешеточных структур и гарантируют, что две полурешетки взаимодействуют соответствующим образом. В частности, каждая полурешетка является двойственной другой. Законы поглощения можно рассматривать как требование того, чтобы соединяющиеся и соединяющиеся полурешетки определяли один и тот же частичный порядок .

Связь между двумя определениями

Теоретико-порядковая решетка порождает две бинарные операции $\vee$ и $\wedge .$ Поскольку для этих операций легко проверить законы коммутативности, ассоциативности и поглощения, они делают $(L,\vee ,\wedge )$ в решетку в алгебраическом смысле.

Обратное также верно. Учитывая алгебраически определенную решетку $(L,\vee ,\wedge ),$ можно определить частичный порядок $\leq$ на $L$ установив

$$a\leq b{\text{ if }}a=a\wedge b,{\text{ or }}$$

$$a\leq b{\text{ if }}b=a\vee b,$$

для всех элементов $a,b\in L.$ Законы поглощения гарантируют эквивалентность обоих определений:

$$a=a\wedge b{\text{ implies }}b=b\vee (b\wedge a)=(a\wedge b)\vee b=a\vee b$$

и дважды для другого направления.

Теперь можно проверить, что введенное таким образом отношение ≤ определяет частичный порядок, в котором двоичные соединения и соединения выполняются посредством исходных операций. $\vee$ и $\wedge .$

Поскольку два определения решетки эквивалентны, можно свободно использовать аспекты любого определения любым способом, отвечающим поставленной цели.

Ограниченная решетка

Ограниченная решетка — это решетка, которая дополнительно имеет наибольший элемент (также называемый максимальным или верхним элементом и обозначаемый $1,$ или через $\top$) и наименьший элемент (также называемый минимумом или дном , обозначаемый $0$ или через $\bot$), которые удовлетворяют

$$0\leq x\leq 1\;{\text{ for every }}x\in L.$$

Ограниченную решетку можно также определить как алгебраическую структуру вида $(L,\vee ,\wedge ,0,1)$ такой, что $(L,\vee ,\wedge )$ представляет собой решётку, $0$ (нижняя часть решетки) — это идентификационный элемент для операции соединения. $\vee ,$ и $1$ (верхушка решетки) является идентификационным элементом для операции встречи. $\wedge .$

$$a\vee 0=a$$

$$a\wedge 1=a$$

Частично упорядоченное множество является ограниченной решеткой тогда и только тогда, когда каждое конечное множество элементов (включая пустое множество) имеет соединение и пересечение. Для каждого элемента $x$ относительно частичного множества совершенно неверно , что ${\text{ for all }}a\in \varnothing ,x\leq a$ и ${\text{ for all }}a\in \varnothing ,a\leq x,$ и, следовательно, каждый элемент ЧУУ является одновременно верхней и нижней границей пустого множества. Это означает, что соединение пустого множества является наименьшим элементом. ${\textstyle \bigvee \varnothing =0,}$ и встреча пустого множества - величайший элемент ${\textstyle \bigwedge \varnothing =1.}$ Это согласуется с ассоциативностью и коммутативностью встреч и соединений: соединение объединения конечных множеств равно соединению объединений множеств, а в двойственном смысле соединение объединения конечных множеств равно соединению встречаются множества множеств, то есть для конечных подмножеств $A$ и $B$ из посета $L,$

$$\bigvee (A\cup B)=\left(\bigvee A\right)\vee \left(\bigvee B\right)$$

и

$$\bigwedge (A\cup B)=\left(\bigwedge A\right)\wedge \left(\bigwedge B\right)$$

держать. принимая $B$ быть пустым множеством,

$$\bigvee (A\cup \varnothing )=\left(\bigvee A\right)\vee \left(\bigvee \varnothing \right)=\left(\bigvee A\right)\vee 0=\bigvee A$$

и

$$\bigwedge (A\cup \varnothing )=\left(\bigwedge A\right)\wedge \left(\bigwedge \varnothing \right)=\left(\bigwedge A\right)\wedge 1=\bigwedge A,$$

что согласуется с тем, что $A\cup \varnothing =A.$

Любую решетку можно вложить в ограниченную, добавив наибольший и наименьший элементы. Более того, каждая непустая конечная решетка ограничена путем объединения (соответственно, пересечения) всех элементов, обозначаемых ${\textstyle 1=\bigvee L=a_{1}\lor \cdots \lor a_{n}}$ (соответственно ${\textstyle 0=\bigwedge L=a_{1}\land \cdots \land a_{n}}$) где $L=\left\{a_{1},\ldots ,a_{n}\right\}$ представляет собой совокупность всех элементов.

с другими

Решетки имеют некоторые связи с семейством группоподобных алгебраических структур . Поскольку встречи и соединения как коммутируют, так и ассоциированы, решетку можно рассматривать как состоящую из двух коммутативных полугрупп, имеющих одну и ту же область определения. Для ограниченной решетки эти полугруппы фактически являются коммутативными моноидами . Закон поглощения — единственное определяющее тождество, свойственное теории решетки. Ограниченную решетку также можно рассматривать как коммутативную установку без аксиомы распределения.

Благодаря коммутативности, ассоциативности и идемпотентности соединения и встречи можно рассматривать как операции над непустыми конечными множествами, а не над парами элементов. В ограниченной решетке соединение и соединение пустого множества также можно определить (как $0$ и $1,$ соответственно). Это делает ограниченные решетки несколько более естественными, чем общие решетки, и многие авторы требуют, чтобы все решетки были ограниченными.

Алгебраическая интерпретация решеток играет существенную роль в универсальной алгебре .

Примеры

• 
  Рис. 1: Подмножества $\{x,y,z\},$ в комплекте включение . Название «решетка» подсказывает форма изображающей ее диаграммы Хассе .
• 
  Рис. 2: Решетка целочисленных делителей 60, упорядоченных по принципу « делит ».
• 
  Рис. : Решетка перегородок 3 $\{1,2,3,4\},$ по заказу компании " Раффин ".
• 
  Рис. 4: Решетка положительных целых чисел, упорядоченная по $\,\leq ,$
• 
  Рис. 5: Решетка пар неотрицательных целых чисел, упорядоченных по компонентам.

• Для любого набора $A,$ совокупность всех подмножеств $A$ (называемый мощности набором $A$) можно упорядочить посредством включения подмножества , чтобы получить решетку, ограниченную $A$ себя и пустое множество. В этой решетке верхняя грань обеспечивается объединением множеств , а нижняя грань — пересечением множеств (см. рис. 1).
• Для любого набора $A,$ совокупность всех конечных подмножеств $A,$ упорядоченный по включению, также является решеткой и будет ограниченным тогда и только тогда, когда $A$ конечно.
• Для любого набора $A,$ совокупность разделов всех $A,$ упорядоченный уточнением , представляет собой решетку (см. рис. 3).
• Положительные целые числа в своем обычном порядке образуют неограниченную решетку под действием операций «min» и «max». 1 – нижний; вершины нет (см. рис. 4).
• Декартов квадрат натуральных чисел, упорядоченный так, что $(a,b)\leq (c,d)$ если $a\leq c{\text{ and }}b\leq d.$ Пара $(0,0)$ — нижний элемент; вершины нет (см. рис. 5).
• Натуральные числа также образуют решетку при выполнении операций взятия наибольшего общего делителя и наименьшего общего кратного с делимостью как отношением порядка: $a\leq b$ если $a$ делит $b.$ $1$ находится внизу; $0$ это топ. Рис. 2 показана конечная подрешетка.
• Всякая полная решетка (см. также ниже ) является (достаточно специфичной) ограниченной решеткой. Этот класс дает начало широкому кругу практических примеров .
• Множество компактных элементов арифметической полной решетки представляет собой решетку с наименьшим элементом, где операции решетки задаются ограничением соответствующих операций арифметической решетки. Это специфическое свойство, которое отличает арифметические решетки от алгебраических решеток , для которых компакты образуют только соединение-полурешетку . Оба эти класса полных решеток изучаются в теории областей .

Дополнительные примеры решеток приведены для каждого из дополнительных свойств, обсуждаемых ниже.

Примеры нерешетчатых решений

Рис. 8: Нерешетчатый ЧУУ: $a$ и $b$ имеют общие нижние границы $0,d,g,h,$ и $i,$ но ни один из них не является наивысшей нижней границей .

Рис. 7: Нерешетчатое частичное множество: $b$ и $c$ имеют общие верхние границы $d,e,$ и $f,$ но ни один из них не является наименьшей верхней границей .

Рис. 6: Нерешетчатый ЧУУ: $c$ и $d$ не имеют общей верхней границы.

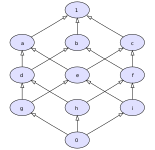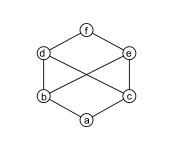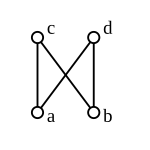Большинство частично упорядоченных множеств не являются решетками, включая следующие.

• Дискретное ЧУУ, то есть ЧУУ такое, что $x\leq y$ подразумевает $x=y,$ является решеткой тогда и только тогда, когда она содержит не более одного элемента. В частности, двухэлементное дискретное ЧУУ не является решеткой.
• Хотя набор $\{1,2,3,6\}$ частично упорядоченный по делимости является решеткой, множество $\{1,2,3\}$ такой порядок не является решеткой, поскольку в паре 2, 3 отсутствует соединение; аналогично, 2, 3 не имеют пересечения в $\{2,3,6\}.$
• Набор $\{1,2,3,12,18,36\}$ частично упорядоченный по делимости не является решеткой. Каждая пара элементов имеет верхнюю и нижнюю границы, но пара 2, 3 имеет три верхних границы, а именно 12, 18 и 36, ни один из которых не является наименьшим из этих трех при делимости (12 и 18 не делят друг друга). Аналогично пара 12, 18 имеет три нижние границы, а именно 1, 2 и 3, ни одна из которых не является наибольшей из этих трех при условии делимости (2 и 3 не делят друг друга).

Морфизмы решеток

Рис. 9: Монотонная карта $f$ между решетками, не сохраняющими ни соединений, ни встреч, поскольку $f(u)\vee f(v)=u^{\prime }\vee u^{\prime }=u^{\prime }$ $\neq$ $1^{\prime }=f(1)=f(u\vee v)$ и $f(u)\wedge f(v)=u^{\prime }\wedge u^{\prime }=u^{\prime }$ $\neq$ $0^{\prime }=f(0)=f(u\wedge v).$

Соответствующее понятие морфизма между двумя решетками легко вытекает из приведенного выше алгебраического определения. Даны две решетки $\left(L,\vee _{L},\wedge _{L}\right)$ и $\left(M,\vee _{M},\wedge _{M}\right),$ решеточный гомоморфизм из L в M — это функция $f:L\to M$ такой, что для всех $a,b\in L:$

$$f\left(a\vee _{L}b\right)=f(a)\vee _{M}f(b),{\text{ and }}$$

$$f\left(a\wedge _{L}b\right)=f(a)\wedge _{M}f(b).$$

Таким образом $f$ является гомоморфизмом двух основных полурешеток . Когда рассматриваются решетки с большей структурой, морфизмы также должны «уважать» дополнительную структуру. В частности, гомоморфизм ограниченной решетки (обычно называемый просто «гомоморфизм решетки») $f$ между двумя ограниченными решетками $L$ и $M$ также должно иметь следующее свойство:

$$f\left(0_{L}\right)=0_{M},{\text{ and }}$$

$$f\left(1_{L}\right)=1_{M}.$$

В формулировке теории порядка эти условия просто утверждают, что гомоморфизм решеток — это функция, сохраняющая бинарные пересечения и соединения. Для ограниченных решеток сохранение наименьшего и наибольшего элементов — это просто сохранение соединения и пересечения пустого множества.

Любой гомоморфизм решеток обязательно монотонен относительно связанного с ним отношения порядка; см. функцию сохранения предела . Обратное неверно: монотонность ни в коем случае не предполагает требуемого сохранения встреч и объединений (см. рис. 9), хотя сохраняющая порядок биекция является гомоморфизмом, если ее обратная также сохраняет порядок.

Учитывая стандартное определение изоморфизмов как обратимых морфизмов, решеточный изоморфизм - это просто биективный решеточный гомоморфизм. Точно так же решеточный эндоморфизм - это решеточный гомоморфизм решетки в себя, а решеточный автоморфизм - это биективный решеточный эндоморфизм. Решетки и их гомоморфизмы образуют категорию .

Позволять $\mathbb {L}$ и $\mathbb {L} '$ будут две решетки с 0 и 1 . Гомоморфизм из $\mathbb {L}$ к $\mathbb {L} '$ называется 0 , 1 — разделяющим тогда и только тогда, когда $f^{-1}\{f(0)\}=\{0\}$ ( $f$ разделяет 0 ) и $f^{-1}\{f(1)\}=\{1\}$ ( $f$ отделяется 1).

Подрешетки

Подрешетка ​ решетки $L$ является подмножеством $L$ это решетка с теми же операциями пересечения и соединения, что и $L.$ То есть, если $L$ представляет собой решетку и $M$ является подмножеством $L$ такая, что для каждой пары элементов $a,b\in M$ оба $a\wedge b$ и $a\vee b$ находятся в $M,$ затем $M$ представляет собой подрешетку $L.$

Подрешетка $M$ решетки $L$ является выпуклой подрешеткой $L,$ если $x\leq z\leq y$ и $x,y\in M$ подразумевает, что $z$ принадлежит $M,$ для всех элементов $x,y,z\in L.$

Свойства решеток

Дополнительная информация: Карта решеток.

Теперь мы введем ряд важных свойств, которые приводят к интересным специальным классам решеток. Один из них — ограниченность — уже обсуждался.

Полнота

Основная статья: Полная решетка

ЧУ-множество называется полной решеткой , если все его подмножества имеют как соединение, так и пересечение. В частности, каждая полная решетка является ограниченной решеткой. В то время как гомоморфизмы ограниченной решетки в целом сохраняют только конечные соединения и пересечения, полные гомоморфизмы решетки необходимы для сохранения произвольных соединений и пересечений.

Каждое ЧУМ, являющееся полной полурешеткой, также является полной решеткой. С этим результатом связано интересное явление, заключающееся в том, что существуют различные конкурирующие понятия гомоморфизма для этого класса ЧУМ, в зависимости от того, рассматриваются ли они как полные решетки, полные соединяющиеся полурешетки, полные пересекающиеся полурешетки или как объединенно-полные или сходящиеся полурешетки. цельные решетки.

«Частичная решетка» не является противоположностью «полной решетки» - скорее, определения «частичная решетка», «решетка» и «полная решетка» становятся все более ограничительными.

Условная полнота

Основная статья: Дедекинд завершен

— Условно полная решетка это решетка, в которой каждое непустое подмножество , имеющее верхнюю границу, имеет соединение (то есть наименьшую верхнюю границу). Такие решетки обеспечивают наиболее прямое обобщение аксиомы полноты действительных чисел . Условно полная решетка — это либо полная решетка, либо полная решетка без максимального элемента. $1,$ его минимальный элемент $0,$ или оба.

Дистрибутивность

Рис. 11: Наименьшая немодулярная (и, следовательно, недистрибутивная) решетка N 5 . $b\leq c$, но $b\vee (a\wedge c)=b$ и $(b\vee a)\wedge c=c$, то модульный закон нарушается. Меченые элементы также нарушают уравнение распределения $c\wedge (a\vee b)=(c\wedge a)\vee (c\wedge b),$ но удовлетворить его двойственное $c\vee (a\wedge b)=(c\vee a)\wedge (c\vee b).$

Рис. 10: Наименьшая недистрибутивная (но модульная) решетка M 3 .

Основная статья: Распределительная решетка

Поскольку в решетках выполняются две бинарные операции, естественно задаться вопросом, распределяется ли одна из них над другой, то есть выполняется ли один или другой из следующих двойственных законов для каждых трех элементов: $a,b,c\in L,$:

Дистрибутивность $\vee$ над $\wedge$

$$a\vee (b\wedge c)=(a\vee b)\wedge (a\vee c).$$

Дистрибутивность $\wedge$ над $\vee$

$$a\wedge (b\vee c)=(a\wedge b)\vee (a\wedge c).$$

Решетка, удовлетворяющая первой или, что то же самое (как оказывается), второй аксиоме, называется дистрибутивной решеткой .Единственные недистрибутивные решетки с числом элементов менее 6 называются M ₃ и N ₅ ; они показаны на рисунках 10 и 11 соответственно. Решетка дистрибутивна тогда и только тогда, когда она не имеет подрешетки, изоморфной M ₃ или N ₅ . Каждая дистрибутивная решетка изоморфна решетке множеств (с объединением и пересечением как соединением и пересечением соответственно).

Для обзора более сильных понятий дистрибутивности, которые подходят для полных решеток и которые используются для определения более специальных классов решеток, таких как фреймы и полностью дистрибутивные решетки , см. дистрибутивность в теории порядка .

Модульность

Основная статья: Модульная решетка

Для некоторых приложений условие дистрибутивности слишком строгое, и часто бывает полезно следующее более слабое свойство. Решетка $(L,\vee ,\wedge )$ является модульным , если для всех элементов $a,b,c\in L,$ имеет место следующее тождество: $(a\wedge c)\vee (b\wedge c)=((a\wedge c)\vee b)\wedge c.$ ( Модульная идентичность )
Это условие эквивалентно следующей аксиоме: $a\leq c$ подразумевает $a\vee (b\wedge c)=(a\vee b)\wedge c.$ ( Модульный закон )
Решетка является модулярной тогда и только тогда, когда она не имеет подрешетки, изоморфной N ₅ (показано на рис. 11). Помимо дистрибутивных решеток, примерами модулярных решеток являются решетка подмодулей модуля ( , ) , решетка двусторонних идеалов кольца модулярная и решетка нормальных подгрупп группы следовательно . Набор термов первого порядка с порядком «более конкретно, чем» представляет собой немодулярную решетку, используемую в автоматизированных рассуждениях .

Полумодульность

Основная статья: Полумодульная решетка

Конечная решетка модулярна тогда и только тогда, когда она полумодулярна как сверху, так и снизу . Для градуированной решетки (верхняя) полумодулярность эквивалентна следующему условию на ранговую функцию $r\colon$

$r(x)+r(y)\geq r(x\wedge y)+r(x\vee y).$

Другим эквивалентным (для градуированных решеток) условием является Биркгофа условие :

для каждого $x$ и $y$ в $L,$ если $x$ и $y$ оба покрытия $x\wedge y,$ затем $x\vee y$ охватывает оба $x$ и $y.$

Решетка называется нижне-полумодулярной, если ее двойственная решетка полумодулярна. Для конечных решеток это означает, что предыдущие условия выполняются при $\vee$ и $\wedge$ поменялись местами, «покрытия» поменялись местами на «покрывается», и неравенство поменялось местами.

Непрерывность и алгебраичность

В теории предметной области естественно стремиться аппроксимировать элементы в частичном порядке «гораздо более простыми» элементами. Это приводит к классу непрерывных частично упорядоченных наборов , состоящему из частично упорядоченных наборов, где каждый элемент может быть получен как верхняя грань направленного набора элементов, находящихся намного ниже элемента. Если для получения этих направленных множеств можно дополнительно ограничить их компактными элементами ЧУМ, то ЧУМ будет четным алгебраическим . Обе концепции можно применить к решеткам следующим образом:

• Непрерывная решетка — это полная решетка, непрерывная как частично упорядоченное множество.
• Алгебраическая решетка — это полная решетка, алгебраическая как частично упорядоченное множество.

Оба этих класса обладают интересными свойствами. Например, непрерывные решетки можно охарактеризовать как алгебраические структуры (с бесконечными операциями), удовлетворяющие определенным тождествам. Хотя для алгебраических решеток такая характеристика неизвестна, их можно описать «синтаксически» с помощью информационных систем Скотта .

Дополнения и псевдодополнения

См. также: псевдодополнение

Позволять $L$ — ограниченная решетка с наибольшим элементом 1 и наименьшим элементом 0. Два элемента $x$ и $y$ из $L$ являются дополнением друг друга тогда и только тогда, когда:

$$x\vee y=1\quad {\text{ and }}\quad x\wedge y=0.$$

В общем, некоторые элементы ограниченной решетки могут не иметь дополнения, а другие могут иметь более одного дополнения. Например, набор $\{0,1/2,1\}$ с обычным упорядочением является ограниченной решеткой, а ${\tfrac {1}{2}}$ не имеет дополнения. В ограниченной решетке N ₅ элемент $a$ имеет два дополнения, а именно. $b$ и $c$ (см. рис. 11). Ограниченная решетка, в которой каждый элемент имеет дополнение, называется решеткой с дополнениями .

Дополненная решетка, которая также является дистрибутивной, является булевой алгеброй . Для дистрибутивной решетки дополнение $x,$ когда он существует, он уникален.

В случае единственности дополнения пишем ${\textstyle \lnot x=y}$ и, что эквивалентно, ${\textstyle \lnot y=x.}$ Соответствующая унарная операция над $L,$ аналог логического отрицания называемое дополнением, вводит в теорию решеток .

Алгебры Гейтинга являются примером дистрибутивных решеток, у некоторых членов которых могут отсутствовать дополнения. Каждый элемент $z$ алгебры Гейтинга, с другой стороны, имеет псевдодополнение , также обозначаемое ${\textstyle \lnot x.}$ Псевдодополнение — величайший элемент $y$ такой, что $x\wedge y=0.$ Если псевдодополнение каждого элемента алгебры Гейтинга на самом деле является дополнением, то алгебра Гейтинга на самом деле является булевой алгеброй.

цепи Джордана

Цепочка ​ из $x_{0}$ к $x_{n}$ это набор $\left\{x_{0},x_{1},\ldots ,x_{n}\right\},$ где $x_{0}<x_{1}<x_{2}<\ldots <x_{n}.$Длина n этой цепочки равна или на единицу меньше количества ее элементов. Цепь максимальна, если $x_{i}$ обложки $x_{i-1}$ для всех $1\leq i\leq n.$

Если для любой пары $x$ и $y,$ где $x<y,$ все максимальные цепи из $x$ к $y$ имеют одинаковую длину, то говорят, что решетка удовлетворяет условию цепочки Жордана–Дедекинда .

Оценено/ранжировано

Решетка $(L,\leq )$ называется graded , иногда ранжированным (но см. в рейтинговом наборе альтернативное значение ), если он может быть оснащен ранговой функцией $r:L\to \mathbb {N}$ иногда, чтобы $\mathbb {Z}$, совместимый с порядком (так что $r(x)<r(y)$ в любое время $x<y$) такой, что всякий раз, когда $y$ обложки $x,$ затем $r(y)=r(x)+1.$ Значение ранговой функции элемента решетки называется его рангом .

Элемент решетки $y$ говорят, что он покрывает другой элемент $x,$ если $y>x,$ но не существует $z$ такой, что $y>z>x.$Здесь, $y>x$ означает $x\leq y$ и $x\neq y.$

Свободные решетки

Основная статья: Свободная решетка

Любой набор $X$ может быть использован для генерации свободной полурешетки $FX.$ Свободная полурешетка определяется как состоящая из всех конечных подмножеств $X,$ с полурешеточной операцией, заданной обычным объединением множеств . Свободная полурешетка обладает свойством универсальности . Для свободной решетки над множеством $X,$ Уитмен дал конструкцию, основанную на полиномах по $X$члены .

решетки

Теперь мы определим некоторые понятия теории порядка, важные для теории решеток. В дальнейшем пусть $x$ быть элементом некоторой решетки $L.$ $x$ называется:

• Присоединитесь к неприводимому, если $x=a\vee b$ подразумевает $x=a{\text{ or }}x=b.$ для всех $a,b\in L.$ Если $L$ есть нижний элемент $0,$ некоторые авторы требуют $x\neq 0$. Когда первое условие обобщается на произвольные соединения $\bigvee _{i\in I}a_{i},$ $x$ называется полностью присоединенным неприводимым (или $\vee$-неприводимый). Двойственное понятие соответствует неприводимости ( $\wedge$-неприводимый). Например, на Рис. 2 элементы 2, 3, 4 и 5 объединены несократимыми, а элементы 12, 15, 20 и 30 — несократимыми. В зависимости от определения нижний элемент 1 и верхний элемент 60 могут считаться или не считаться несократимыми для соединения и несоединяемыми для соединения соответственно. В решетке действительных чисел обычного порядка каждый элемент несократим по объединению, но ни один из них не является полностью неприводимым по объединению.
• Присоединяйтесь к Прайму, если $x\leq a\vee b$ подразумевает $x\leq a{\text{ or }}x\leq b.$ Опять же, некоторые авторы требуют $x\neq 0$, хотя это необычно. Это тоже можно обобщить, чтобы получить понятие « полностью присоединиться к простому числу» . Двойственное понятие — это встретить простое число . Каждый простой элемент соединения также неприводим к соединению, и каждый элемент простого соединения также неприводим. Обратное справедливо, если $L$ является распределительным.

Позволять $L$ иметь нижний элемент 0. Элемент $x$ из $L$ является атомом , если $0<x$ и не существует элемента $y\in L$ такой, что $0<y<x.$ Затем $L$ называется:

• Атомарный , если для каждого ненулевого элемента $x$ из $L,$ существует атом $a$ из $L$ такой, что $a\leq x;$
• Атомистический, если каждый элемент $L$ является супремумом атомов.

Однако многие источники и математические сообщества используют термин «атомарный» в значении «атомистический», как определено выше.

Понятия идеалов и двойственное понятие фильтров относятся к определенным видам подмножеств частично упорядоченного множества и поэтому важны для теории решеток. Подробности можно найти в соответствующих записях.

См. также

• Присоединяйтесь и знакомьтесь – концепция в теории порядка
• Карта решеток - Понятие в математике
• Ортодополненная решетка
• Общий порядок - заказ, все элементы которого сопоставимы.
• Идеал - непустое, ограниченное сверху, закрытое вниз подмножество и фильтр (двойные понятия).
• Косая решетка - страницы алгебраической структуры , отображающие описания викиданных в качестве запасного варианта (обобщение для некоммутативного соединения и встречи)
• Эйлерова решетка
• Решетка поста - решетка всех клонов (наборов логических связок, замкнутых по композиции и содержащих все проекции) на двухэлементном множестве {0, 1}, упорядоченных по включению. Страницы, отображающие описания викиданных в качестве запасного варианта.
• Решетка Тамари - математический объект, образованный порядком заключения выражения в скобки. Страницы, отображающие описания викиданных в качестве запасного варианта.
• Решетка Янга – Фибоначчи
• 0,1-простая решетка

использующие теорию

Обратите внимание, что во многих приложениях множества представляют собой лишь частичные решетки: не каждая пара элементов имеет пересечение или соединение.

• Бессмысленная топология
• Решетка подгрупп
• Спектральное пространство
• Инвариантное подпространство
• Оператор закрытия
• Абстрактная интерпретация
• Решетка подчинения
• нечетких множеств Теория
• Алгебраизации логики первого порядка
• Семантика языков программирования
• Теория предметной области
• Онтология (информатика)
• Множественное наследование
• Анализ формальных концепций и Lattice Miner (теория и инструмент)
• Фильтр Блума
• Информационный поток
• Порядковая оптимизация
• Квантовая логика
• Медианный график
• Пространство знаний
• Регулярное изучение языка
• Аналогичное моделирование

Ссылки

Монографии доступны бесплатно онлайн:

• Беррис, Стэнли Н. и Санкаппанавар, Х.П., 1981. Курс универсальной алгебры. Спрингер-Верлаг. ISBN   3-540-90578-2 .
• Джипсен, Питер и Генри Роуз, Разновидности решеток , Конспекты лекций по математике, 1533 г., Springer Verlag, 1992. ISBN   0-387-56314-8 .

Элементарные тексты, рекомендуемые для людей с ограниченной математической зрелостью :

• Доннеллан, Томас, 1968. Теория решеток . Пергамон.
• Гретцер, Джордж , 1971. Теория решеток: первые концепции и распределительные решетки . У. Х. Фриман.

Стандартный современный вводный текст, несколько сложнее приведенного выше:

• Дэйви, бакалавр; Пристли, HA (2002), Введение в решетки и порядок , Cambridge University Press , ISBN  978-0-521-78451-1

Передовые монографии:

• Гаррет Биркгоф , 1967. Теория решеток , 3-е изд. Том. 25 публикаций коллоквиума AMS. Американское математическое общество .
• Роберт П. Дилворт и Кроули, Питер, 1973. Алгебраическая теория решеток . Прентис-Холл. ISBN   978-0-13-022269-5 .
• Гретцер, Джордж (2003). Общая теория решеток (второе изд.). Базель: Биркхойзер. ISBN  978-3-7643-6996-5 .

На свободных решетках:

• Р. Фриз, Дж. Джезек и Дж. Б. Нэйшн, 1985. «Свободные решетки». Математические обзоры и монографии Vol. 42. Математическая ассоциация Америки .
• Джонстон, ПТ , 1982. Каменные пространства . Кембриджские исследования по высшей математике 3. Издательство Кембриджского университета.

К истории теории решеток:

• Штепанка Билова (2001). Эдуард Фукс (ред.). Теория решеток — ее рождение и жизнь (PDF) . Прометей. стр. 250–257.
• Биркгоф, Гаррет (1948). Теория решеток (2-е изд.). Учебник с многочисленными ссылками в сносках.
• Шлимм, Дирк (ноябрь 2011 г.). «О творческой роли аксиоматики. Открытие решеток Шредером, Дедекиндом, Биркгофом и другими». Синтезируйте . 183 (1): 47–68. CiteSeerX   10.1.1.594.8898 . дои : 10.1007/s11229-009-9667-9 . S2CID   11012081 . Краткое изложение истории решеток.
• Дедекинд, Рихард (1897), «О разложении чисел по их наибольшим общим делителям» (PDF) , Braunschweiger Festschrift , doi : 10.24355/dbbs.084-200908140200-2

О приложениях теории решеток:

• Гаррет Биркгоф (1967). Джеймс С. Эббот (ред.). Чем решетки могут вам помочь? . Ван Ностранд. Оглавление

Внешние ссылки

• «Решётчато-упорядоченная группа» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Вайсштейн, Эрик В. «Решетка» . Математический мир .
• JB Nation, Заметки по теории решеток , конспекты курса, переработанные в 2017 г.
• Ральф Фриз, «Домашняя страница теории решеток» .
• Последовательность OEIS A006966 (Количество немаркированных решеток с n элементами)