Диаграмма Венна

Диаграмма Венна — это широко используемый стиль диаграмм , показывающий логические отношения между множествами , популяризированный Джоном Венном (1834–1923) в 1880-х годах. Диаграммы используются для обучения элементарной теории множеств и для иллюстрации простых взаимосвязей множеств в теории вероятности , логике , статистике , лингвистике и информатике . Диаграмма Венна использует простые замкнутые кривые, нарисованные на плоскости, для представления множеств. Очень часто эти кривые представляют собой круги или эллипсы.

Подобные идеи были предложены до Венна, например, Кристианом Вайзе в 1712 году (« Nucleus Logicoe Wiesianoe ») и Леонардом Эйлером (« Письма к немецкой принцессе ») в 1768 году. Идея была популяризирована Венном в « Символической логике» , главе V «Диаграмматическое представление», опубликованной в 1881 году.

Подробности [ править ]

Диаграмма Венна, также называемая диаграммой множеств или логической диаграммой , показывает все возможные логические отношения между конечным набором различных множеств. изображены На этих диаграммах элементы в виде точек на плоскости, а множества — в виде областей внутри замкнутых кривых. Диаграмма Венна состоит из нескольких перекрывающихся замкнутых кривых, обычно кругов, каждая из которых представляет набор. Точки внутри кривой, помеченной S, представляют элементы набора S , а точки за пределами границы представляют элементы, не входящие в S. набор Это поддается интуитивной визуализации; например, набор всех элементов, которые являются членами обоих наборов S и T , обозначенный S ∩ T и прочитанный как «пересечение S и T », визуально представлен областью перекрытия S и T. областей ^[1]

В диаграммах Венна кривые всячески перекрываются, показывая все возможные связи между множествами. Таким образом, они являются частным случаем диаграмм Эйлера , которые не обязательно отображают все отношения. Диаграммы Венна были придуманы Джоном Венном около 1880 года. Они используются для преподавания элементарной теории множеств, а также для иллюстрации простых отношений множеств в теории вероятности, логики, статистики, лингвистики и информатики.

Диаграмма Венна, в которой площадь каждой фигуры пропорциональна количеству содержащихся в ней элементов, называется пропорциональной по площади (или масштабированной ) диаграммой Венна .

Пример [ править ]

В этом примере задействованы два набора существ, представленных здесь в виде цветных кругов. Оранжевый круг представляет все виды существ, имеющих две ноги. Синий круг представляет существ, которые могут летать. Каждый отдельный вид существ можно представить как точку где-нибудь на диаграмме. Живые существа, имеющие две ноги и способные летать, например попугаи, тогда входят в оба набора, поэтому они соответствуют точкам в области, где перекрываются синий и оранжевый круги. Эта перекрывающаяся область будет содержать только те элементы (в данном примере существа), которые являются членами как оранжевого набора (двуногие существа), так и синего набора (летающие существа).

Люди и пингвины двуногие, поэтому они показаны в оранжевом круге, но, поскольку они не умеют летать, они появляются в левой части оранжевого круга, где он не пересекается с синим кругом. Комары умеют летать, но имеют шесть, а не две ноги, поэтому точка для комаров находится в той части синего круга, которая не пересекается с оранжевым. Существа, которые не являются ни двуногими, ни умеющими летать (например, киты и пауки), будут представлены точками за пределами обоих кругов.

Объединенная область двух множеств называется их объединением и обозначается A ∪ B , где A — оранжевый круг, а B — синий. ^[2]В союз в данном случае входят все живые существа, которые либо двуногие, либо умеют летать (или и то, и другое). Область, входящая как в A, так и в B, где эти два множества перекрываются, называется пересечением A и B и обозначается A ∩ B . ^[2]

История [ править ]

Витраж с диаграммой Венна в колледже Гонвилл и Кей, Кембридж

Диаграммы Венна были представлены в 1880 году Джоном Венном в статье, озаглавленной «О схематическом и механическом представлении предложений и рассуждений». ^[3] в «Философском журнале» и «Журнале науки» , ^[4] о различных способах представления предложений в виде диаграмм. ^[5]^[6]^[7] Использование этих типов диаграмм в формальной логике , по мнению Фрэнка Раски и Марка Уэстона, появилось раньше Венна, но «справедливо связано» с ним, поскольку он «всесторонне исследовал и формализовал их использование и был первым, кто их обобщил». ^[8]

Диаграммы Венна очень похожи на диаграммы Эйлера , которые были изобретены Леонардом Эйлером в 18 веке. ^{[примечание 1]}^[9]^[10] Маргарет Барон отметила, что Лейбниц (1646–1716) создал подобные диаграммы до Эйлера в 17 веке, но большая часть их не была опубликована. ^[11] Она также наблюдает еще более ранние диаграммы, подобные Эйлеру, написанные Рамоном Луллием в 13 веке. ^[12]

Венн не использовал термин «диаграмма Венна» и называл эту концепцию «эйлеровыми кругами». ^[7] Он познакомился с диаграммами Эйлера в 1862 году и написал, что диаграммы Венна пришли ему в голову «много позже», когда он пытался адаптировать диаграммы Эйлера к булевой логике . ^[13] В первом предложении своей статьи 1880 года Венн написал, что диаграммы Эйлера были единственным схематическим представлением логики, получившим «какое-либо общее признание». ^[5]^[6]

Венн рассматривал свои диаграммы как педагогический инструмент, аналогичный проверке физических концепций посредством эксперимента. В качестве примера их применения он отметил, что диаграмма из трех наборов может показать силлогизм : «Все А есть некоторое В» . Никакое B не является C. никаким Следовательно, никакое А не является никаким С ». ^[13]

Чарльз Л. Доджсон (Льюис Кэрролл) включил «Метод диаграмм Венна», а также «Метод диаграмм Эйлера» в «Приложение, адресованное учителям» своей книги « Символическая логика» (4-е издание, опубликованное в 1896 году). Термин «диаграмма Венна» позже был использован Кларенсом Ирвингом Льюисом в 1918 году в его книге « Обзор символической логики» . ^[8]^[14]

В 20 веке диаграммы Венна получили дальнейшее развитие. Дэвид Уилсон Хендерсон показал в 1963 году, что существование n -диаграммы Венна с n -кратной вращательной симметрией подразумевает, что n — простое число . ^[15]Он также показал, что такие симметричные диаграммы Венна существуют, когда n равно пяти или семи. В 2002 году Питер Гамбургер нашел симметричные диаграммы Венна для n = 11, а в 2003 году Григгс, Киллиан и Сэвидж показали, что симметричные диаграммы Венна существуют для всех остальных простых чисел. Эти объединенные результаты показывают, что вращательно-симметричные диаграммы Венна существуют тогда и только тогда, когда n — простое число. ^[16]

Диаграммы Венна и диаграммы Эйлера были включены в обучение теории множеств в рамках нового математического движения в 1960-х годах. С тех пор они также были включены в учебную программу по другим областям, таким как чтение. ^[17]

Обзор [ править ]

Пересечение двух множеств $~A\cap B$
Союз двух комплектов $~A\cup B$
Симметричная разница двух наборов $A~\triangle ~B$
Относительное дополнение A ( слева) к B (справа) $A^{c}\cap B~=~B\setminus A$
Абсолютное дополнение A в U $A^{c}~=~U\setminus A$

Диаграмма Венна состоит из набора простых замкнутых кривых, нарисованных на плоскости. По словам Льюиса, ^[14] «принцип этих диаграмм заключается в том, что классы [или множества ] представляются областями в таком отношении друг к другу, что все возможные логические отношения этих классов могут быть указаны на одной и той же диаграмме. То есть диаграмма изначально оставляет место для любых возможное отношение классов, а также фактическое или заданное отношение затем можно указать, указав, что некоторая конкретная область имеет значение NULL или не является NULL». ^[14]^: 157

Диаграммы Венна обычно состоят из перекрывающихся кругов . Внутренняя часть круга символически представляет элементы набора, а внешняя — элементы, не являющиеся членами набора. Например, на диаграмме Венна, состоящей из двух наборов, один круг может представлять группу всех деревянных предметов, а другой круг может представлять набор всех столов. Перекрывающаяся область, или пересечение , тогда будет представлять собой набор всех деревянных столов. Можно использовать и другие формы, кроме кругов, как показано ниже на собственных диаграммах высшего набора Венна. Диаграммы Венна обычно не содержат информации об относительных или абсолютных размерах ( мощности ) множеств. То есть это схематические изображения, как правило, не в масштабе.

Диаграммы Венна аналогичны диаграммам Эйлера. Однако диаграмма Венна для n наборов компонентов должна содержать все 2 ^н гипотетически возможные зоны, соответствующие некоторой комбинации включения или исключения в каждом из наборов компонентов. ^[18]Диаграммы Эйлера содержат только реально возможные зоны в данном контексте. На диаграммах Венна заштрихованная зона может обозначать пустую зону, тогда как на диаграмме Эйлера соответствующая зона отсутствует на диаграмме. Например, если один набор представляет молочные продукты , а другой — сыры , диаграмма Венна содержит зону для сыров, не являющихся молочными продуктами. Если предположить, что в контексте сыр означает некоторый тип молочного продукта, на диаграмме Эйлера зона сыра полностью содержится внутри зоны молочных продуктов — зоны для (несуществующего) немолочного сыра нет. Это означает, что по мере увеличения количества контуров диаграммы Эйлера обычно становятся менее визуально сложными, чем эквивалентная диаграмма Венна, особенно если количество непустых пересечений невелико. ^[19]

Разницу между диаграммами Эйлера и Венна можно увидеть на следующем примере. Возьмите три комплекта:

$A=\{1,\,2,\,5\}$
$B=\{1,\,6\}$
$C=\{4,\,7\}$

Диаграммы Эйлера и Венна этих множеств:

Диаграмма Эйлера
Диаграмма Венна

Расширения для большего количества наборов [ править ]

Диаграммы Венна обычно представляют два или три набора, но есть формы, которые допускают более высокие числа. Как показано ниже, четыре пересекающиеся сферы образуют диаграмму Венна высшего порядка, которая имеет симметрию симплекса и может быть представлена визуально. 16 пересечений соответствуют вершинам тессеракта ( или ячейкам 16-клетки соответственно).

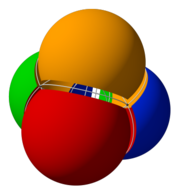При большем числе множеств некоторая потеря симметрии диаграмм неизбежна. Венн стремился найти «симметричные фигуры… элегантные сами по себе». ^[9]это представляло большее количество наборов, и он разработал элегантную диаграмму из четырех наборов с использованием эллипсов (см. Ниже). Он также дал конструкцию диаграмм Венна для любого числа множеств, где каждая последующая кривая, ограничивающая множество, чередуется с предыдущими кривыми, начиная с диаграммы из трех кругов.

Конструкция Венна для четырех наборов (для вычислений используйте код Грея , цифра 1 означает наличие в наборе, а цифра 0 означает отсутствие в наборе)
Конструкция Венна на пять сетов
Конструкция Венна на шесть подходов
Диаграмма Венна из четырех множеств с использованием эллипсов
Непример: эта диаграмма Эйлера является не диаграммой Венна для четырех наборов, поскольку в ней всего 14 областей вместо 2. ⁴= 16 регионов (включая белый регион); не существует области, где встречаются только желтый и синий или только красный и зеленый круги.
Пятимножественная диаграмма Венна с использованием конгруэнтных эллипсов в пятикратном вращательно-симметричном расположении, разработанная Бранко Грюнбаумом . Ярлыки были упрощены для большей читабельности; например, A обозначает A ∩ B ^с ∩ С ^с ∩ Д ^с ∩ Е ^с, а BCE обозначает A ^с ∩ B ∩ C ∩ D ^с ∩ Э .
Шестимножественная диаграмма Венна, состоящая только из треугольников (интерактивная версия)

Диаграммы Эдвардса-Венна [ править ]

Три комплекта
Четыре комплекта
Пять комплектов
Шесть комплектов

Энтони Уильям Фэрбенк Эдвардс построил серию диаграмм Венна для большего числа множеств путем сегментирования поверхности сферы, которые стали известны как диаграммы Эдвардса-Венна. ^[20]Например, три набора можно легко представить, взяв три полусферы сферы под прямым углом ( x = 0, y = 0 и z = 0). К изображению можно добавить четвертый набор, взяв кривую, подобную шву теннисного мяча, который вьется вверх и вниз вокруг экватора и так далее. Полученные наборы затем можно спроецировать обратно на плоскость, чтобы получить диаграммы зубчатых колес с увеличивающимся количеством зубцов, как показано здесь. Эти схемы были разработаны при проектировании витража в память о Венне. ^[20]

Другие диаграммы [ править ]

Диаграммы Эдвардса-Венна топологически эквивалентны диаграммам, разработанным Бранко Грюнбаумом , которые были основаны на пересекающихся многоугольниках с увеличивающимся числом сторон. Они также являются двумерными представлениями гиперкубов .

Генри Джон Стивен Смит разработал аналогичные диаграммы из n -множеств, используя синусоидальные кривые. ^[20] с рядом уравнений

y_{i}={\frac {\sin \left(2^{i}x\right)}{2^{i}}}{\text{ where }}0\leq i\leq n-1{\text{ and }}i\in \mathbb {N} .

Чарльз Лютвидж Доджсон (также известный как Льюис Кэрролл) разработал диаграмму из пяти множеств, известную как квадрат Кэрролла . Хоакин и Бойлс, с другой стороны, предложили дополнительные правила для стандартной диаграммы Венна, чтобы учесть определенные проблемные случаи. Например, что касается вопроса представления сингулярных утверждений, они предлагают рассматривать круг диаграммы Венна как представление множества вещей и использовать логику первого порядка и теорию множеств, чтобы рассматривать категориальные утверждения как утверждения о множествах. Кроме того, они предлагают рассматривать единичные утверждения как утверждения о членстве во множестве . Так, например, чтобы представить утверждение «а есть F» на этой переработанной диаграмме Венна, маленькая буква «а» может быть помещена внутри круга, обозначающего множество F. ^[21]

Связанные понятия [ править ]

Диаграммы Венна соответствуют таблицам истинности предложений. $x\in A$ , $x\in B$ и т. д. в том смысле, что каждая область диаграммы Венна соответствует одной строке таблицы истинности. ^[22]^[23]Этот тип также известен как диаграмма Джонстона. Другой способ представления множеств — R-диаграммы Джона Ф. Рэндольфа .

См. также [ править ]

Экзистенциальный граф ( Чарльз Сандерс Пирс )
Логические связки
Информационная диаграмма
Диаграмма Маркванда (и как дальнейший вывод диаграмма Вейча и карта Карно )
Сферический октаэдр . Стереографическая проекция правильного октаэдра образует трехкомпонентную диаграмму Венна в виде трех ортогональных больших кругов, каждый из которых делит пространство на две половины.
Стэнхоуп Демонстратор
Модель трех кругов
Три раза
Рыба-пузырь

Примечания [ править ]

↑ В «Письмах Эйлера к немецкой принцессе на различные физические и философские темы» (Санкт-Петербург, Россия: Императорская Академия наук, 1768), том 2, страницы 95–126. Однако в статье Венна он предполагает, что схематическая идея возникла раньше Эйлера и принадлежит Кристиану Вайзе или Иоганну Кристиану Ланге (в книге Ланге Nucleus Logicae Weisianae (1712)).

Ссылки [ править ]

^ «Пересечение множеств» . web.mnstate.edu . Архивировано из оригинала 04 августа 2020 г. Проверено 05 сентября 2020 г.
^ Перейти обратно: ^а ^б «Множества и диаграммы Венна» . www.mathsisfun.com . Проверено 05 сентября 2020 г.
^ Венн, Джон. «О схематическом и механическом представлении предложений и рассуждений» (PDF) . Пенн Инжиниринг .
^ «Философский журнал: журнал теоретической, экспериментальной и прикладной физики» . Тейлор и Фрэнсис . Проверено 6 августа 2021 г.
^ Перейти обратно: ^а ^б Венн, Джон (июль 1880 г.). «I. О схематическом и механическом представлении предложений и рассуждений» (PDF) . Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 5. 10 (59): 1–18. дои : 10.1080/14786448008626877 . Архивировано (PDF) из оригинала 16 мая 2017 г. [1] [2]
^ Перейти обратно: ^а ^б Венн, Джон (1880). «Об использовании геометрических диаграмм для разумного представления логических предложений» . Труды Кембриджского философского общества . 4 : 47–59.
^ Перейти обратно: ^а ^б Сандифер, Эд (2003). «Как это сделал Эйлер» (PDF) . МАА Онлайн . Математическая ассоциация Америки (МАА) . Проверено 26 октября 2009 г.
^ Перейти обратно: ^а ^б Раски, Фрэнк ; Уэстон, Марк (18 июня 2005 г.). «Обзор диаграмм Венна» . Электронный журнал комбинаторики .
^ Перейти обратно: ^а ^б Венн, Джон (1881). Символическая логика . Макмиллан . п. 108 . Проверено 9 апреля 2013 г.
^ Мак Куин, Гейланд (октябрь 1967 г.). Логическая диаграмма (PDF) (Диссертация). Университет Макмастера . Архивировано из оригинала (PDF) 14 апреля 2017 г. Проверено 14 апреля 2017 г. (Примечание. Имеет подробную историю эволюции логических диаграмм, включая, помимо прочего, диаграмму Венна.)
^ Лейбниц, Готфрид Вильгельм (1903) [ок. 1690]. «О формах логики через линии лидерства». В Кутюра, Луи (ред.). Неопубликованные произведения и фрагменты Лейбница (на латыни). стр. 292–321.
^ Барон, Маргарет Э. (май 1969 г.). «Заметка об историческом развитии логических диаграмм». Математический вестник . 53 (384): 113–125. дои : 10.2307/3614533 . JSTOR 3614533 . S2CID 125364002 .
^ Перейти обратно: ^а ^б Вербургт, Лукас М. (апрель 2023 г.). «Венн за диаграммой». Математика сегодня . Том. 59, нет. 2. Институт математики и ее приложений . стр. 53–55.
^ Перейти обратно: ^а ^б ^с Льюис, Кларенс Ирвинг (1918). Обзор символической логики . Беркли: Издательство Калифорнийского университета .
^ Хендерсон, Дэвид Уилсон (апрель 1963 г.). «Диаграммы Венна для более чем четырех классов». Американский математический ежемесячник . 70 (4): 424–426. дои : 10.2307/2311865 . JSTOR 2311865 .
^ Раски, Фрэнк ; Сэвидж, Карла Д .; Вагон, Стэн (декабрь 2006 г.). «В поисках простых симметричных диаграмм Венна» (PDF) . Уведомления АМС . 53 (11): 1304–1311.
^ «Стратегии понимания чтения диаграмм Венна» . Архивировано из оригинала 29 апреля 2009 г. Проверено 20 июня 2009 г.
^ Вайсштейн, Эрик В. «Диаграмма Венна» . mathworld.wolfram.com . Проверено 05 сентября 2020 г.
^ «Диаграммы Эйлера 2004: Брайтон, Великобритания: 22–23 сентября» . Проект «Рассуждение с помощью диаграмм», Кентский университет. 2004 . Проверено 13 августа 2008 г.
^ Перейти обратно: ^а ^б ^с Эдвардс, Энтони Уильям Фэрбанк (2004). Зубчатые колеса разума: история диаграмм Венна . Балтимор, Мэриленд, США: Издательство Университета Джонса Хопкинса . п. 65. ИСБН 978-0-8018-7434-5 . .
^ Хоакин, Иеремия Ховен; Бойлз, Роберт Джеймс М. (июнь 2017 г.). «Преподавание силлогистической логики с помощью переработанной диаграммной техники Венна» . Преподавание философии . 40 (2): 161–180. дои : 10.5840/teachphil201771767 . Архивировано из оригинала 21 ноября 2018 г. Проверено 12 мая 2020 г.
^ Гримальди, Ральф П. (2004). Дискретная и комбинаторная математика . Бостон: Аддисон-Уэсли . п. 143. ИСБН 978-0-201-72634-3 .
^ Джонсон, Дэвид Л. (2001). «3.3 Законы» . Элементы логики через числа и множества . Серия Springer по математике для студентов. Берлин, Германия: Springer-Verlag . п. 62 . ISBN 978-3-540-76123-5 .

Дальнейшее чтение [ править ]

Махмудиан, Эбадолла С .; Резаи, М.; Ватан, Ф. (март 1987 г.). «Обобщение диаграммы Венна» (PDF) . Восемнадцатая ежегодная иранская математическая конференция . Тегеран и Исфахан, Иран. Архивировано из оригинала (PDF) 1 мая 2017 г. Проверено 1 мая 2017 г.
Эдвардс, Энтони Уильям Фэрбанк (7 января 1989 г.). «Диаграммы Венна для многих множеств». Новый учёный . 121 (1646): 51–56.
Уоткинсон, Джон (1990). «4.10. Расстояние Хэмминга». Кодирование для цифровой записи . Стоунхэм, Массачусетс, США: Focal Press . стр. 94–99, складной на заднем рукаве. ISBN 978-0-240-51293-8 . (Примечание: в книгу входит трехстраничный разворот семибитной цилиндрической диаграммы Венна.)
Стюарт, Ян (июнь 2003 г.) [1992]. «Глава 4. Шестеренки разума» . Еще одна прекрасная математика, в которую вы меня втянули (перепечатка 1-го изд.). Минеола, Нью-Йорк, США: Dover Publications, Inc. ( WH Freeman ). стр. 51–64. ISBN 978-0-486-43181-9 .
Гласснер, Эндрю (2004). «Венн и сейчас». Морфы, кряквы и монтажи: компьютерное воображение . Уэлсли, Массачусетс, США: AK Peters . стр. 161–184. ISBN 978-1568812311 .
Мамакани, Халег; Раски, Фрэнк (27 июля 2012 г.). «Новая роза: первая простая симметричная диаграмма 11 Венна» . п. 6452. arXiv : 1207.6452 . Бибкод : 2012arXiv1207.6452M . Архивировано из оригинала 1 мая 2017 г. Проверено 1 мая 2017 г.

Внешние ссылки [ править ]

[NB_1-9] В «Письмах Эйлера к немецкой принцессе на различные физические и философские темы» (Санкт-Петербург, Россия: Императорская Академия наук, 1768), том 2, страницы 95–126. Однако в статье Венна он предполагает, что схематическая идея возникла раньше Эйлера и принадлежит Кристиану Вайзе или Иоганну Кристиану Ланге (в книге Ланге Nucleus Logicae Weisianae (1712)).

[Peil_2020-1] «Пересечение множеств» . web.mnstate.edu . Архивировано из оригинала 04 августа 2020 г. Проверено 05 сентября 2020 г.

[:1-2] Перейти обратно: ^а ^б «Множества и диаграммы Венна» . www.mathsisfun.com . Проверено 05 сентября 2020 г.

[Venn_2014-3] Венн, Джон. «О схематическом и механическом представлении предложений и рассуждений» (PDF) . Пенн Инжиниринг .

[PM-4] «Философский журнал: журнал теоретической, экспериментальной и прикладной физики» . Тейлор и Фрэнсис . Проверено 6 августа 2021 г.

[Venn1880_1-5] Перейти обратно: ^а ^б Венн, Джон (июль 1880 г.). «I. О схематическом и механическом представлении предложений и рассуждений» (PDF) . Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 5. 10 (59): 1–18. дои : 10.1080/14786448008626877 . Архивировано (PDF) из оригинала 16 мая 2017 г. [1] [2]

[Venn1880_2-6] Перейти обратно: ^а ^б Венн, Джон (1880). «Об использовании геометрических диаграмм для разумного представления логических предложений» . Труды Кембриджского философского общества . 4 : 47–59.

[Sandifer2003-7] Перейти обратно: ^а ^б Сандифер, Эд (2003). «Как это сделал Эйлер» (PDF) . МАА Онлайн . Математическая ассоциация Америки (МАА) . Проверено 26 октября 2009 г.

[Ruskey2005-8] Перейти обратно: ^а ^б Раски, Фрэнк ; Уэстон, Марк (18 июня 2005 г.). «Обзор диаграмм Венна» . Электронный журнал комбинаторики .

[Venn1881-10] Перейти обратно: ^а ^б Венн, Джон (1881). Символическая логика . Макмиллан . п. 108 . Проверено 9 апреля 2013 г.

[Gailand_1967-11] Мак Куин, Гейланд (октябрь 1967 г.). Логическая диаграмма (PDF) (Диссертация). Университет Макмастера . Архивировано из оригинала (PDF) 14 апреля 2017 г. Проверено 14 апреля 2017 г. (Примечание. Имеет подробную историю эволюции логических диаграмм, включая, помимо прочего, диаграмму Венна.)

[Leibniz_1690-12] Лейбниц, Готфрид Вильгельм (1903) [ок. 1690]. «О формах логики через линии лидерства». В Кутюра, Луи (ред.). Неопубликованные произведения и фрагменты Лейбница (на латыни). стр. 292–321.

[Baron_1969-13] Барон, Маргарет Э. (май 1969 г.). «Заметка об историческом развитии логических диаграмм». Математический вестник . 53 (384): 113–125. дои : 10.2307/3614533 . JSTOR 3614533 . S2CID 125364002 .

[Maths_Today-14] Перейти обратно: ^а ^б Вербургт, Лукас М. (апрель 2023 г.). «Венн за диаграммой». Математика сегодня . Том. 59, нет. 2. Институт математики и ее приложений . стр. 53–55.

[Lewis1918-15] Перейти обратно: ^а ^б ^с Льюис, Кларенс Ирвинг (1918). Обзор символической логики . Беркли: Издательство Калифорнийского университета .

[Henderson_1963-16] Хендерсон, Дэвид Уилсон (апрель 1963 г.). «Диаграммы Венна для более чем четырех классов». Американский математический ежемесячник . 70 (4): 424–426. дои : 10.2307/2311865 . JSTOR 2311865 .

[Ruskey_2006-17] Раски, Фрэнк ; Сэвидж, Карла Д .; Вагон, Стэн (декабрь 2006 г.). «В поисках простых симметричных диаграмм Венна» (PDF) . Уведомления АМС . 53 (11): 1304–1311.

[Strategies-18] «Стратегии понимания чтения диаграмм Венна» . Архивировано из оригинала 29 апреля 2009 г. Проверено 20 июня 2009 г.

[Weisstein_2020-19] Вайсштейн, Эрик В. «Диаграмма Венна» . mathworld.wolfram.com . Проверено 05 сентября 2020 г.

[Kent_2004-20] «Диаграммы Эйлера 2004: Брайтон, Великобритания: 22–23 сентября» . Проект «Рассуждение с помощью диаграмм», Кентский университет. 2004 . Проверено 13 августа 2008 г.

[Edwards_2004-21] Перейти обратно: ^а ^б ^с Эдвардс, Энтони Уильям Фэрбанк (2004). Зубчатые колеса разума: история диаграмм Венна . Балтимор, Мэриленд, США: Издательство Университета Джонса Хопкинса . п. 65. ИСБН 978-0-8018-7434-5 . .

[Joaquin_2017-22] Хоакин, Иеремия Ховен; Бойлз, Роберт Джеймс М. (июнь 2017 г.). «Преподавание силлогистической логики с помощью переработанной диаграммной техники Венна» . Преподавание философии . 40 (2): 161–180. дои : 10.5840/teachphil201771767 . Архивировано из оригинала 21 ноября 2018 г. Проверено 12 мая 2020 г.

[Grimaldi_2004-23] Гримальди, Ральф П. (2004). Дискретная и комбинаторная математика . Бостон: Аддисон-Уэсли . п. 143. ИСБН 978-0-201-72634-3 .

[Johnson_2001-24] Джонсон, Дэвид Л. (2001). «3.3 Законы» . Элементы логики через числа и множества . Серия Springer по математике для студентов. Берлин, Германия: Springer-Verlag . п. 62 . ISBN 978-3-540-76123-5 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[примечание 1]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

v т Это Теория множеств
Overview	Set (mathematics)
Axioms	Adjunction Choice countable dependent global Constructibility (V=L) Determinacy Extensionality Infinity Limitation of size Pairing Power set Regularity Union Martin's axiom Axiom schema replacement specification
Operations	Cartesian product Complement (i.e. set difference) De Morgan's laws Disjoint union Identities Intersection Power set Symmetric difference Union
Concepts Methods	Almost Cardinality Cardinal number (large) Class Constructible universe Continuum hypothesis Diagonal argument Element ordered pair tuple Family Forcing One-to-one correspondence Ordinal number Set-builder notation Transfinite induction Venn diagram
Set types	Amorphous Countable Empty Finite (hereditarily) Filter base subbase Ultrafilter Fuzzy Infinite (Dedekind-infinite) Recursive Singleton Subset · Superset Transitive Uncountable Universal
Theories	Alternative Axiomatic Naive Cantor's theorem Zermelo General Principia Mathematica New Foundations Zermelo–Fraenkel von Neumann–Bernays–Gödel Morse–Kelley Kripke–Platek Tarski–Grothendieck
Paradoxes Problems	Russell's paradox Suslin's problem Burali-Forti paradox
Set theorists	Paul Bernays Georg Cantor Paul Cohen Richard Dedekind Abraham Fraenkel Kurt Gödel Thomas Jech John von Neumann Willard Quine Bertrand Russell Thoralf Skolem Ernst Zermelo