Вероятностная мера

В математике вероятностная мера — это действительнозначная функция, определенная на множестве событий в σ-алгебре , которая удовлетворяет свойствам меры , таким как счетная аддитивность . ^[1] Разница между вероятностной мерой и более общим понятием меры (которое включает в себя такие понятия, как площадь или объем ) заключается в том, что вероятностная мера должна присваивать значение 1 всему пространству.

Интуитивно, свойство аддитивности говорит о том, что вероятность, приписываемая мере объединению двух непересекающихся (взаимоисключающих) событий, должна быть суммой вероятностей событий; например, значение, присвоенное результату «1 или 2» при броске игральной кости, должно быть суммой значений, присвоенных результатам «1» и «2».

Вероятностные меры находят применение в самых разных областях: от физики до финансов и биологии.

Определение [ править ]

Вероятностная *мера,* отображающая σ-алгебру для $2^{3}$ событий с единичным интервалом .

Требования к заданной функции $\mu$ быть вероятностной мерой на σ-алгебре, таковы:

$\mu$ должен возвращать результаты в единичном интервале $[0,1],$ возвращение $0$ для пустого множества и $1$ для всего пространства.
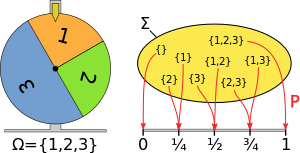
$\mu$ должно удовлетворять свойству счетной аддитивности , которое для всех счетных коллекций $E_{1},E_{2},\ldots$ попарно непересекающихся множеств : $\mu \left(\bigcup _{i\in \mathbb {N} }E_{i}\right)=\sum _{i\in \mathbb {N} }\mu (E_{i}).$

Например, даны три элемента 1, 2 и 3 с вероятностями $1/4,1/4$ и $1/2,$ значение, присвоенное $\{1,3\}$ является $1/4+1/2=3/4,$ как на схеме справа.

Условная вероятность, основанная на пересечении событий, определяется как:

\mu (B\mid A)={\frac {\mu (A\cap B)}{\mu (A)}}.

^[2]удовлетворяет требованиям вероятностной меры до тех пор, пока

\mu (A)

не равен нулю. ^[3]

Вероятностные меры отличаются от более общего понятия нечетких мер , в котором нет требования, чтобы сумма нечетких значений составляла $1,$ и аддитивное свойство заменяется отношением порядка, основанным на включении множества .

Примеры приложений [ править ]

Во многих случаях статистическая физика использует *вероятностные меры* , но не все используемые ею меры являются вероятностными мерами. ^[4]^[5]

Рыночные меры , которые присваивают вероятности пространствам финансового рынка на основе фактических движений рынка, являются примерами вероятностных мер, представляющих интерес для математических финансов ; например, в ценообразовании производных финансовых инструментов . ^[6] Например, нейтральная к риску мера — это вероятностная мера, которая предполагает, что текущая стоимость активов представляет собой ожидаемую стоимость будущих выплат, полученных по отношению к той же нейтральной к риску мере (т. е. рассчитанной с использованием соответствующей функции плотности нейтральной к риску), и дисконтированы по безрисковой ставке . Если существует уникальная вероятностная мера, которую необходимо использовать для оценки активов на рынке, то рынок называется полным рынком . ^[7]

Не все меры, которые интуитивно представляют случайность или вероятность, являются вероятностными мерами. Например, хотя фундаментальным понятием системы в статистической механике является пространство меры, такие меры не всегда являются вероятностными мерами. ^[4] В общем, в статистической физике, если мы рассматриваем предложения вида «вероятность того, что система S примет состояние A равно p», геометрия системы не всегда приводит к определению вероятностной меры при конгруэнтности , хотя и может это сделать. то же самое и в случае систем всего с одной степенью свободы. ^[5]

Вероятностные меры также используются в математической биологии . ^[8] Например, при сравнительном анализе последовательностей можно определить меру вероятности для вероятности того, что вариант может быть допустимым для аминокислоты в последовательности. ^[9]

Ультрафильтры можно понимать как $\{0,1\}$ -значные вероятностные меры, позволяющие проводить множество интуитивных доказательств, основанных на мерах. Например, теорема Хиндмана может быть доказана путем дальнейшего исследования этих мер и, в частности, их свертки .

См. также [ править ]

Борелевская мера - мера, определенная на всех открытых множествах топологического пространства.
Нечеткая мера - теория обобщенных мер, в которой аддитивное свойство заменяется более слабым свойством монотонности.
Мера Хаара - левоинвариантная (или правоинвариантная) мера на локально компактной топологической группе.
Мера Лебега - понятие площади в любом измерении.
Показатель Мартингейла – показатель вероятности.
Функция набора – функция преобразования наборов в числа.
Распределение вероятностей

Ссылки [ править ]

^ Введение в теорию вероятности Джорджа Г. Руссаса, 2004 г. ISBN 0-12-599022-7 стр. 47
^ Деккинг, Фредерик Мишель; Краайкамп, Корнелис; Лопухаа, Хендрик Пауль; Местер, Людольф Эрвин (2005). «Современное введение в теорию вероятности и статистики» . Спрингеровские тексты в статистике . дои : 10.1007/1-84628-168-7 . ISSN 1431-875X .
^ Вероятность, случайные процессы и эргодические свойства Роберта М. Грея, 2009 г. ISBN 1-4419-1089-1 стр. 163
^ Jump up to: ^а ^б Курс математики для студентов-физиков, Том 2 , Пол Бамберг, Шломо Штернберг, 1991 г. ISBN 0-521-40650-1 стр. 802
^ Jump up to: ^а ^б Концепция вероятности в статистической физике Яира М. Гутмана, 1999 г. ISBN 0-521-62128-3 стр. 149
^ Количественные методы ценообразования деривативов Доминго Тавелла, 2002 г. ISBN 0-471-39447-5 стр. 11
↑ Необратимые решения в условиях неопределенности , Светлана Боярченко, Серж Левендорский, 2007 г. ISBN 3-540-73745-6 стр. 11
^ Математические методы в биологии Дж. Дэвида Логана, Уильяма Р. Волесенски, 2009 г. ISBN 0-470-52587-8 стр. 195
^ Открытие биомолекулярных механизмов с помощью вычислительной биологии Фрэнка Эйзенхабера, 2006 г. ISBN 0-387-34527-2 стр. 127

Дальнейшее чтение [ править ]

Биллингсли, Патрик (1995). Вероятность и мера . Джон Уайли. ISBN 0-471-00710-2 .
Эш, Роберт Б.; Долеанс-Дейд, Кэтрин А. (1999). Теория вероятностей и меры . Академическая пресса. ISBN 0-12-065202-1 .
Различение вероятностной меры, функции и распределения

Внешние ссылки [ править ]

СМИ, связанные с мерой вероятности, на Викискладе?

[1] Введение в теорию вероятности Джорджа Г. Руссаса, 2004 г. ISBN 0-12-599022-7 стр. 47

[2] Деккинг, Фредерик Мишель; Краайкамп, Корнелис; Лопухаа, Хендрик Пауль; Местер, Людольф Эрвин (2005). «Современное введение в теорию вероятности и статистики» . Спрингеровские тексты в статистике . дои : 10.1007/1-84628-168-7 . ISSN 1431-875X .

[3] Вероятность, случайные процессы и эргодические свойства Роберта М. Грея, 2009 г. ISBN 1-4419-1089-1 стр. 163

[stern-4] Jump up to: ^а ^б Курс математики для студентов-физиков, Том 2 , Пол Бамберг, Шломо Штернберг, 1991 г. ISBN 0-521-40650-1 стр. 802

[gut-5] Jump up to: ^а ^б Концепция вероятности в статистической физике Яира М. Гутмана, 1999 г. ISBN 0-521-62128-3 стр. 149

[6] Количественные методы ценообразования деривативов Доминго Тавелла, 2002 г. ISBN 0-471-39447-5 стр. 11

[7] Необратимые решения в условиях неопределенности , Светлана Боярченко, Серж Левендорский, 2007 г. ISBN 3-540-73745-6 стр. 11

[8] Математические методы в биологии Дж. Дэвида Логана, Уильяма Р. Волесенски, 2009 г. ISBN 0-470-52587-8 стр. 195

[9] Открытие биомолекулярных механизмов с помощью вычислительной биологии Фрэнка Эйзенхабера, 2006 г. ISBN 0-387-34527-2 стр. 127

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]