Счетное множество

В математике множество , считается счетным если оно либо конечно , либо его можно привести во взаимно однозначное соответствие с множеством натуральных чисел . ^[а]Эквивалентно, множество счетно, если существует функция, инъективная из него в натуральные числа; это означает, что каждый элемент набора может быть связан с уникальным натуральным числом или что элементы набора можно считать по одному, хотя подсчет может никогда не завершиться из-за бесконечного числа элементов.

Говоря более техническим языком, предполагая аксиому счетного выбора , набор является счетным , если его мощность (количество элементов набора) не превышает мощность натуральных чисел. Счетное множество, которое не является конечным, называется счетным .

Концепция приписывается Георгу Кантору , который доказал существование несчетных множеств , то есть множеств, которые не счетны; например набор действительных чисел .

Примечание по терминологии [ править ]

Хотя термины «счетный» и «счетный бесконечный», определенные здесь, довольно распространены, эта терминология не является универсальной. ^[1] Альтернативный стиль использует слово «исчисляемое» для обозначения того, что здесь называется «счетно-бесконечным», и «самое большее» - «счетное» для обозначения того, что здесь называется «счетным». ^[2]^[3]

Термины перечислимые ^[4] и счетный ^[5]^[6] также может использоваться, например, для обозначения счетной и счетной бесконечности соответственно, ^[7] определения различаются, и необходимо соблюдать осторожность, учитывая разницу с рекурсивно перечислимыми . ^[8]

Определение [ править ]

Множество $S$ счетно , если:

Его мощность $|S|$ меньше или равно $\aleph _{0}$ ( aleph-null ), мощность множества натуральных чисел $\mathbb {N}$ . ^[9]
Существует инъективная функция из $S$ к $\mathbb {N}$ . ^[10]^[11]
$S$ пусто или существует сюръективная функция из $\mathbb {N}$ к $S$ . ^[11]
Существует биективное отображение между $S$ и подмножество $\mathbb {N}$ . ^[12]
$S$ либо конечно ( $|S|<\aleph _{0}$ ) или счетно бесконечным. ^[5]

Все эти определения эквивалентны.

Множество $S$ бесконечно счетно , если:

Его мощность $|S|$ это точно $\aleph _{0}$ . ^[9]
Существует инъективное и сюръективное (и, следовательно, биективное ) отображение между $S$ и $\mathbb {N}$ .
$S$ имеет личную переписку с $\mathbb {N}$ . ^[13]
Элементы $S$ можно расположить в бесконечной последовательности $a_{0},a_{1},a_{2},\ldots$ , где $a_{i}$ отличается от $a_{j}$ для $i\neq j$ и каждый элемент $S$ указан. ^[14]^[15]

Множество является несчетным , если оно несчетно, т. е. его мощность больше, чем $\aleph _{0}$ . ^[9]

История [ править ]

В 1874 году в своей первой статье по теории множеств Кантор доказал, что множество действительных чисел неисчислимо, показав тем самым, что не все бесконечные множества счетны. ^[16] В 1878 году он использовал взаимно-однозначные соответствия для определения и сравнения мощностей. ^[17] В 1883 году он расширил натуральные числа своими бесконечными порядковыми номерами и использовал наборы порядковых номеров для создания бесконечного множества наборов, имеющих разную бесконечную мощность. ^[18]

Введение [ править ]

Набор представляет собой совокупность элементов и может быть описан разными способами. Один из способов — просто перечислить все его элементы; например, набор, состоящий из целых чисел 3, 4 и 5, можно обозначить $\{3,4,5\}$ , называемая формой реестра. ^[19]Однако это эффективно только для небольших наборов; для больших наборов это потребует много времени и чревато ошибками. Вместо перечисления каждого отдельного элемента иногда используется многоточие («...») для обозначения множества элементов между начальным и конечным элементом в наборе, если автор считает, что читатель может легко догадаться, что представляет собой .... ; например, $\{1,2,3,\dots ,100\}$ предположительно обозначает набор целых чисел от 1 до 100. Однако даже в этом случае все равно можно перечислить все элементы, поскольку число элементов в наборе конечно. Если пронумеровать элементы множества 1, 2 и т. д. до $n$ , это дает нам обычное определение «множеств размера $n$ ".

Некоторые множества бесконечны ; в этих наборах более $n$ элементы, где $n$ любое целое число, которое можно указать. (Независимо от того, насколько велико указанное целое число $n$ такое, как $n=10^{1000}$ , бесконечные множества имеют более $n$ элементов.) Например, набор натуральных чисел, обозначаемых $\{0,1,2,3,4,5,\dots \}$ , ^[а]имеет бесконечно много элементов, и мы не можем использовать никакое натуральное число для определения его размера. Может показаться естественным разделить множества на разные классы: объединить все множества, содержащие один элемент; все множества, содержащие два элемента вместе; ...; наконец, соберите все бесконечные множества и считайте, что они имеют одинаковый размер. Эта точка зрения хорошо работает для счетных бесконечных множеств и была преобладающим предположением до работы Георга Кантора. Например, существует бесконечно много нечетных целых чисел, бесконечно много четных целых чисел, а также бесконечно много целых чисел в целом. Мы можем считать, что все эти наборы имеют одинаковый «размер», потому что мы можем расположить вещи так, что для каждого целого числа существует отдельное четное целое число:

\ldots \,-\!2\!\rightarrow \!-\!4,\,-\!1\!\rightarrow \!-\!2,\,0\!\rightarrow \!0,\,1\!\rightarrow \!2,\,2\!\rightarrow \!4\,\cdots

или, в более общем смысле,

n\rightarrow 2n

(см. картинку). Здесь мы организовали целые и четные целые числа во взаимно однозначное соответствие (или биекцию ), которое представляет собой функцию , которая отображает между двумя наборами так, что каждый элемент каждого набора соответствует одному элементу в другом. набор. Это математическое понятие «размера», мощности, заключается в том, что два множества имеют одинаковый размер тогда и только тогда, когда между ними существует биекция. Мы называем все множества, находящиеся во взаимно однозначном соответствии с целыми числами, счетными и говорим, что они имеют мощность.

\aleph _{0}

.

Георг Кантор показал, что не все бесконечные множества счетно бесконечны. Например, действительные числа не могут быть приведены во взаимно однозначное соответствие натуральным числам (неотрицательным целым числам). Множество действительных чисел имеет большую мощность, чем множество натуральных чисел, и называется несчетным.

Формальный обзор [ править ]

По определению, набор $S$ счетно , если существует биекция между $S$ и подмножество натуральных чисел $\mathbb {N} =\{0,1,2,\dots \}$ . Например, определите соответствие

a\leftrightarrow 1,\ b\leftrightarrow 2,\ c\leftrightarrow 3

Поскольку каждый элемент

S=\{a,b,c\}

сочетается ровно с одним элементом

\{1,2,3\}

и что наоборот, это определяет биекцию и показывает,

S

является счетным. Аналогичным образом мы можем показать, что все конечные множества счетны.

Что касается случая бесконечных множеств, то множество $S$ счетно бесконечно, если существует биекция между $S$ и все $\mathbb {N}$ . В качестве примера рассмотрим множества $A=\{1,2,3,\dots \}$ , набор положительных целых чисел и $B=\{0,2,4,6,\dots \}$ , набор четных целых чисел. Мы можем показать, что эти множества счетно бесконечны, продемонстрировав биекцию натуральных чисел. Этого можно добиться с помощью заданий $n\leftrightarrow n+1$ и $n\leftrightarrow 2n$ , так что

{\begin{matrix}0\leftrightarrow 1,&1\leftrightarrow 2,&2\leftrightarrow 3,&3\leftrightarrow 4,&4\leftrightarrow 5,&\ldots \\[6pt]0\leftrightarrow 0,&1\leftrightarrow 2,&2\leftrightarrow 4,&3\leftrightarrow 6,&4\leftrightarrow 8,&\ldots \end{matrix}}

Всякое счетное множество счетно, а всякое бесконечное счетное множество счетно бесконечно. Более того, любое подмножество натуральных чисел счетно, и в более общем смысле:

Теорема . Подмножество счетного множества счетно. ^[20]

Набор всех упорядоченных пар натуральных чисел ( декартово произведение двух наборов натуральных чисел, $\mathbb {N} \times \mathbb {N}$ счетно бесконечно, в чем можно убедиться, пройдя по пути, подобному показанному на рисунке:

Полученное отображение происходит следующим образом:

0\leftrightarrow (0,0),1\leftrightarrow (1,0),2\leftrightarrow (0,1),3\leftrightarrow (2,0),4\leftrightarrow (1,1),5\leftrightarrow (0,2),6\leftrightarrow (3,0),\ldots

Это отображение охватывает все такие упорядоченные пары.

Эта форма треугольного отображения рекурсивно обобщается на $n$ - кортежи натуральных чисел, т.е. $(a_{1},a_{2},a_{3},\dots ,a_{n})$ где $a_{i}$ и $n$ являются натуральными числами путем многократного сопоставления первых двух элементов числа. $n$ -кортеж к натуральному числу. Например, $(0,2,3)$ можно записать как $((0,2),3)$ . Затем $(0,2)$ отображается на 5, так что $((0,2),3)$ карты в $(5,3)$ , затем $(5,3)$ отображается в 39. Поскольку это другой двухкортеж, это пара, такая как $(a,b)$ , отображается в другое натуральное число, разницы между двумя кортежами по одному элементу достаточно, чтобы гарантировать отображение кортежей в разные натуральные числа. Итак, инъекция из набора $n$ -кортежи множества натуральных чисел $\mathbb {N}$ доказано. Для набора $n$ -кортежи, состоящие из декартова произведения конечного числа различных множеств, каждый элемент в каждом кортеже соответствует натуральному числу, поэтому каждый кортеж можно записать натуральными числами, тогда для доказательства теоремы применяется та же логика.

Теорема . Декартово произведение конечного числа счетных множеств счетно. ^[21]^[б]

Набор всех целых чисел $\mathbb {Z}$ и множество всех рациональных чисел $\mathbb {Q}$ может интуитивно показаться гораздо большим, чем $\mathbb {N}$ . Но внешность может быть обманчивой. Если пару рассматривать как числитель и знаменатель обыкновенной дроби (дроби в виде $a/b$ где $a$ и $b\neq 0$ являются целыми числами), то для каждой положительной дроби можно найти соответствующее ей отдельное натуральное число. Это представление включает также натуральные числа, поскольку каждое натуральное число $n$ это тоже дробь $n/1$ . Таким образом, мы можем заключить, что положительных рациональных чисел ровно столько, сколько положительных целых чисел. Это также верно для всех рациональных чисел, как можно увидеть ниже.

Теорема — $\mathbb {Z}$ (набор всех целых чисел) и $\mathbb {Q}$ (множество всех рациональных чисел) счетны. ^[с]

множество алгебраических чисел . Аналогичным образом счетно ^[23]^[д]

Иногда полезно использовать более одного сопоставления: набор $A$ быть показанным как счетное, взаимно однозначно отображается (инъекция) в другой набор $B$ , затем $A$ оказывается счетным, если $B$ однозначно отображается на множество натуральных чисел. Например, набор положительных рациональных чисел можно легко взаимно однозначно отобразить в набор пар натуральных чисел (двойки), потому что $p/q$ карты в $(p,q)$ . Поскольку набор пар натуральных чисел взаимно однозначно отображается (фактически взаимно однозначное соответствие или биекция) в набор натуральных чисел, как показано выше, набор положительных рациональных чисел доказывается как счетный.

Теорема . Любое конечное объединение счетных множеств счетно. ^[24]^[25]^[Это]

Зная, что существуют несчетные множества, мы можем задаться вопросом, можно ли продвинуть этот последний результат дальше. Ответ — «да» и «нет», мы можем расширить его, но для этого нам нужно принять новую аксиому.

Теорема — (предполагая аксиому счетного выбора ) Объединение счетного числа счетных множеств счетно. ^[ф]

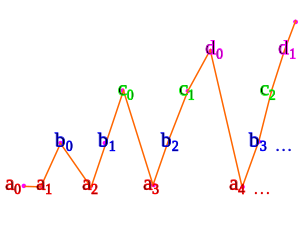
Перечисление счетного числа счетных множеств

Например, даны счетные множества ${\textbf {a}},{\textbf {b}},{\textbf {c}},\dots$ , мы сначала присваиваем каждому элементу каждого набора кортеж, затем присваиваем каждому кортежу индекс, используя вариант треугольного перечисления, который мы видели выше:

{\begin{array}{c|c|c }{\text{Index}}&{\text{Tuple}}&{\text{Element}}\\\hline 0&(0,0)&{\textbf {a}}_{0}\\1&(0,1)&{\textbf {a}}_{1}\\2&(1,0)&{\textbf {b}}_{0}\\3&(0,2)&{\textbf {a}}_{2}\\4&(1,1)&{\textbf {b}}_{1}\\5&(2,0)&{\textbf {c}}_{0}\\6&(0,3)&{\textbf {a}}_{3}\\7&(1,2)&{\textbf {b}}_{2}\\8&(2,1)&{\textbf {c}}_{1}\\9&(3,0)&{\textbf {d}}_{0}\\10&(0,4)&{\textbf {a}}_{4}\\\vdots &&\end{array}}

Нам нужна аксиома счетного выбора для индексации всех множеств. ${\textbf {a}},{\textbf {b}},{\textbf {c}},\dots$ одновременно.

Теорема . Множество всех последовательностей натуральных чисел конечной длины счетно.

Этот набор представляет собой объединение последовательностей длины 1, последовательностей длины 2 и последовательностей длины 3, каждая из которых представляет собой счетное множество (конечное декартово произведение). Итак, речь идет о счетном объединении счетных множеств, которое счетно по предыдущей теореме.

Теорема . Множество всех конечных подмножеств натуральных чисел счетно.

Элементы любого конечного подмножества можно упорядочить в конечную последовательность. Существует только счетное число конечных последовательностей, поэтому существует только счетное число конечных подмножеств.

Теорема — Пусть $S$ и $T$ быть наборами.

Если функция $f:S\to T$ является инъективным и $T$ тогда счетно $S$ является счетным.
Если функция $g:S\to T$ является сюръективным и $S$ тогда счетно $T$ является счетным.

Они следуют из определений счетного множества как инъективных/сюръективных функций. ^[г]

Теорема Кантора утверждает, что если $A$ представляет собой набор и ${\mathcal {P}}(A)$ - это его набор мощности , т.е. набор всех подмножеств $A$ , то не существует сюръективной функции из $A$ к ${\mathcal {P}}(A)$ . Доказательство приведено в статье Теорема Кантора . Как непосредственное следствие этого и приведенной выше основной теоремы мы имеем:

Предложение — множество ${\mathcal {P}}(\mathbb {N} )$ не является счетным; т.е. оно неисчислимо .

Более подробно этот результат см. в диагональном аргументе Кантора .

Множество действительных чисел несчетно, ^[час] то же самое относится и к множеству всех бесконечных последовательностей натуральных чисел.

модель теории счетна множеств Минимальная

Если существует набор, который является стандартной моделью (см. внутреннюю модель ) теории множеств ZFC, то существует минимальная стандартная модель (см. Конструируемая вселенная ). Теорему Левенхайма – Скулема можно использовать, чтобы показать, что эта минимальная модель счетна. Тот факт, что понятие «несчетность» имеет смысл даже в этой модели, и в частности, что эта модель M содержит элементы, которые:

подмножества M , следовательно, счетные,
но несчетно с точки зрения М ,

на заре теории множеств считалось парадоксальным; см. парадокс Скулема подробнее .

Минимальная стандартная модель включает все алгебраические числа и все эффективно вычислимые трансцендентные числа , а также многие другие виды чисел.

Всего заказов [ править ]

Счетные множества можно полностью упорядочить различными способами, например:

Колодцы-заказы (см. также порядковый номер ):
- Обычный порядок натуральных чисел (0, 1, 2, 3, 4, 5,...)
- Целые числа в порядке (0, 1, 2, 3, ...; −1, −2, −3, ...)
Другое ( не очень заказы):
- Обычный порядок целых чисел (..., −3, −2, −1, 0, 1, 2, 3, ...)
- Обычный порядок рациональных чисел (Невозможно явно записать в виде упорядоченного списка!)

В обоих примерах порядка скважин здесь любое подмножество имеет наименьший элемент ; и в обоих примерах заказов, отличных от скважин, некоторые подмножества не имеют наименьшего элемента . Это ключевое определение, которое определяет, является ли общий заказ также порядком скважины.

См. также [ править ]

Примечания [ править ]

^ Перейти обратно: ^а ^б Поскольку существует очевидная биекция между $\mathbb {N}$ и $\mathbb {N} ^{*}=\{1,2,3,\dots \}$ , не имеет значения, считать ли 0 натуральным числом или нет. В любом случае, эта статья соответствует ISO 31-11 и стандартному соглашению в математической логике , которое принимает 0 как натуральное число.
^ Доказательство: обратите внимание, что $\mathbb {N} \times \mathbb {N}$ счетна как следствие определения, поскольку функция $f:\mathbb {N} \times \mathbb {N} \to \mathbb {N}$ данный $f(m,n)=2^{m}\cdot 3^{n}$ является инъективным. ^[22] Отсюда следует, что декартово произведение любых двух счетных множеств счетно, потому что если $A$ и $B$ два счетных множества, есть сюръекции $f:\mathbb {N} \to A$ и $g:\mathbb {N} \to B$ . Так $f\times g:\mathbb {N} \times \mathbb {N} \to A\times B$ является сюръекцией из счетного множества $\mathbb {N} \times \mathbb {N}$ на съемочную площадку $A\times B$ и следствие означает $A\times B$ является счетным. Этот результат обобщается на декартово произведение любого конечного набора счетных множеств, и доказательство следует индукцией по количеству множеств в наборе.
^ Доказательство: целые числа $\mathbb {Z}$ счетны, поскольку функция $f:\mathbb {Z} \to \mathbb {N}$ данный $f(n)=2^{n}$ если $n$ неотрицательен и $f(n)=3^{-n}$ если $n$ отрицательна, является инъективной функцией. Рациональные числа $\mathbb {Q}$ счетны, поскольку функция $g:\mathbb {Z} \times \mathbb {N} \to \mathbb {Q}$ данный $g(m,n)=m/(n+1)$ является сюръекцией из счетного множества $\mathbb {Z} \times \mathbb {N}$ к рациональному объяснению $\mathbb {Q}$ .
^ Доказательство: по определению, каждое алгебраическое число (включая комплексные числа) является корнем многочлена с целыми коэффициентами. Учитывая алгебраическое число $\alpha$ , позволять $a_{0}x^{0}+a_{1}x^{1}+a_{2}x^{2}+\cdots +a_{n}x^{n}$ — многочлен с целыми коэффициентами такой, что $\alpha$ это $k$ -й корень многочлена, где корни сортируются по абсолютному значению от меньшего к большему, а затем сортируются по аргументу от меньшего к большему. Мы можем определить функцию инъекции (т.е. взаимно-однозначную) $f:\mathbb {A} \to \mathbb {Q}$ данный $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ , где $p_{n}$ это $n$ -е простое число .
^ Доказательство: Если $A_{i}$ является счетным множеством для каждого $i$ в $I=\{1,\dots ,n\}$ , то для каждого $i$ существует сюръективная функция $g_{i}:\mathbb {N} \to A_{i}$ и, следовательно, функция $G:I\times \mathbf {N} \to \bigcup _{i\in I}A_{i},$ данный $G(i,m)=g_{i}(m)$ это сюръективность. С $I\times \mathbb {N}$ счетно, объединение ${\textstyle \bigcup _{i\in I}A_{i}}$ является счетным.
^ Доказательство : Как и в конечном случае, но $I=\mathbb {N}$ и мы используем аксиому счетного выбора, чтобы выбрать для каждого $i$ в $\mathbb {N}$ сюръекция $g_{i}$ из непустой совокупности сюръекций из $\mathbb {N}$ к $A_{i}$ . ^[26] Заметим, что поскольку мы рассматриваем сюръекцию $G:\mathbf {N} \times \mathbf {N} \to \bigcup _{i\in I}A_{i}$ , а не инъекции, нет требования, чтобы множества были непересекающимися.
^ Доказательство : для (1) заметим, что если $T$ счетно, существует инъективная функция $h:T\to \mathbb {N}$ . Тогда, если $f:S\to T$ инъективен состав $h\circ f:S\to \mathbb {N}$ является инъективным, поэтому $S$ является счетным. Для (2) заметим, что если $S$ счетно либо $S$ пусто или существует сюръективная функция $h:\mathbb {N} \to S$ . Тогда, если $g:S\to T$ является сюръективным либо $S$ и $T$ оба пусты, или композиция $g\circ h:\mathbb {N} \to T$ является сюръективным. В любом случае $T$ является счетным.
^ См. первое доказательство несчетности Кантора , а также свойство конечного пересечения # Приложения для топологического доказательства.

Цитаты [ править ]

^ Манетти, Марко (19 июня 2015 г.). Топология . Спрингер. п. 26. ISBN 978-3-319-16958-3 .
^ Рудин 1976 , Глава 2
^ Люди 2016 , с. 181
^ Камке 1950 , с. 2
^ Перейти обратно: ^а ^б Ланг 1993 , §2 главы I
^ Апостол 1969 , с. 23, глава 1.14
^ Тьерри, Виалар (4 апреля 2017 г.). Справочник по математике . Совет директоров - Книги по запросу. п. 24. ISBN 978-2-9551990-1-5 .
^ Мукерджи, Субир Кумар (2009). Первый курс реального анализа . Академические издательства. п. 22. ISBN 978-81-89781-90-3 .
^ Перейти обратно: ^а ^б ^с Якуб, Аладдин М. (24 октября 2014 г.). Введение в металогику . Бродвью Пресс. ISBN 978-1-4604-0244-3 .
^ Сингх, Тедж Бахадур (17 мая 2019 г.). Введение в топологию . Спрингер. п. 422. ИСБН 978-981-13-6954-4 .
^ Перейти обратно: ^а ^б Кацуракис, Николаос; Варварука, Евгений (2 января 2018 г.). Наглядное введение в современный анализ . ЦРК Пресс. ISBN 978-1-351-76532-9 .
^ Халмош 1960 , с. 91
^ Камке 1950 , с. 2
^ Длаб, Властимил; Уильямс, Кеннет С. (9 июня 2020 г.). Приглашение к алгебре: сборник ресурсов для учителей, студентов старших курсов и аспирантов по математике . Всемирная научная. п. 8. ISBN 978-981-12-1999-3 .
^ Люди 2016 , с. 182
^ Стиллвелл, Джон К. (2010), Дороги к бесконечности: математика истины и доказательства , CRC Press, стр. 10, ISBN 9781439865507 Открытие Кантором бесчисленных множеств в 1874 году было одним из самых неожиданных событий в истории математики. До 1874 года большинство людей даже не считали бесконечность законным математическим предметом, поэтому необходимость различать счетную и несчетную бесконечность не могла быть и вообразима.
^ Кантор 1878, с. 242.
^ Феррейрос 2007, стр. 268, 272–273.
^ «Что такое наборы и форма состава?» . экспии . 09.05.2021. Архивировано из оригинала 18 сентября 2020 г.
^ Халмош 1960 , с. 91
^ Халмош 1960 , с. 92
^ Авельсгаард 1990 , с. 182
^ Камке 1950 , с. 3–4
^ Авельсгаард 1990 , с. 180
^ Флетчер и Пэтти 1988 , с. 187
^ Хрбачек, Карел; Джех, Томас (22 июня 1999 г.). Введение в теорию множеств, третье издание, переработанное и расширенное . ЦРК Пресс. п. 141. ИСБН 978-0-8247-7915-3 .

Ссылки [ править ]

Апостол, Том М. (июнь 1969 г.), Исчисление с несколькими переменными и линейная алгебра с приложениями , Исчисление, том. 2 (2-е изд.), Нью-Йорк: John Wiley + Sons, ISBN 978-0-471-00007-5
Авелсгаард, Кэрол (1990), Основы высшей математики , Скотт, Форесман и компания, ISBN 0-673-38152-8
Кантор, Георг (1878), «Вклад в теорию многообразий» , Журнал чистой и прикладной математики , 1878 (84): 242–248, doi : 10.1515/crell-1878-18788413 , S2CID 123695365
Феррейрос, Хосе (2007), Лабиринт мысли: история теории множеств и ее роль в математической мысли (2-е исправленное издание), Биркхойзер, ISBN 978-3-7643-8349-7
Флетчер, Питер; Пэтти, К. Уэйн (1988), Основы высшей математики , Бостон: Издательская компания PWS-KENT, ISBN 0-87150-164-3
Халмос, Пол Р. (1960), Наивная теория множеств , D. Van Nostand Company, Inc. Перепечатано Springer-Verlag, Нью-Йорк, 1974. ISBN 0-387-90092-6 (издание Springer-Verlag). Перепечатано издательством Martino Fine Books, 2011 г. ISBN 978-1-61427-131-4 (издание в мягкой обложке).
Камке, Эрих (1950), Теория множеств , Дуврская серия по математике и физике, Нью-Йорк: Дувр, ISBN 978-0486601410
Ланг, Серж (1993), Реальный и функциональный анализ , Берлин, Нью-Йорк: Springer-Verlag, ISBN 0-387-94001-4
Рудин, Уолтер (1976), Принципы математического анализа , Нью-Йорк: McGraw-Hill, ISBN 0-07-054235-Х
Тао, Теренс (2016). «Бесконечные множества» . Анализ И. Тексты и чтения по математике. Том. 37 (Третье изд.). Сингапур: Спрингер. стр. 181–210. дои : 10.1007/978-981-10-1789-6_8 . ISBN 978-981-10-1789-6 .

[ZeroN-1] Перейти обратно: ^а ^б Поскольку существует очевидная биекция между $\mathbb {N}$ и $\mathbb {N} ^{*}=\{1,2,3,\dots \}$ , не имеет значения, считать ли 0 натуральным числом или нет. В любом случае, эта статья соответствует ISO 31-11 и стандартному соглашению в математической логике , которое принимает 0 как натуральное число.

[24] Доказательство: обратите внимание, что $\mathbb {N} \times \mathbb {N}$ счетна как следствие определения, поскольку функция $f:\mathbb {N} \times \mathbb {N} \to \mathbb {N}$ данный $f(m,n)=2^{m}\cdot 3^{n}$ является инъективным. ^[22] Отсюда следует, что декартово произведение любых двух счетных множеств счетно, потому что если $A$ и $B$ два счетных множества, есть сюръекции $f:\mathbb {N} \to A$ и $g:\mathbb {N} \to B$ . Так $f\times g:\mathbb {N} \times \mathbb {N} \to A\times B$ является сюръекцией из счетного множества $\mathbb {N} \times \mathbb {N}$ на съемочную площадку $A\times B$ и следствие означает $A\times B$ является счетным. Этот результат обобщается на декартово произведение любого конечного набора счетных множеств, и доказательство следует индукцией по количеству множеств в наборе.

[25] Доказательство: целые числа $\mathbb {Z}$ счетны, поскольку функция $f:\mathbb {Z} \to \mathbb {N}$ данный $f(n)=2^{n}$ если $n$ неотрицательен и $f(n)=3^{-n}$ если $n$ отрицательна, является инъективной функцией. Рациональные числа $\mathbb {Q}$ счетны, поскольку функция $g:\mathbb {Z} \times \mathbb {N} \to \mathbb {Q}$ данный $g(m,n)=m/(n+1)$ является сюръекцией из счетного множества $\mathbb {Z} \times \mathbb {N}$ к рациональному объяснению $\mathbb {Q}$ .

[27] Доказательство: по определению, каждое алгебраическое число (включая комплексные числа) является корнем многочлена с целыми коэффициентами. Учитывая алгебраическое число $\alpha$ , позволять $a_{0}x^{0}+a_{1}x^{1}+a_{2}x^{2}+\cdots +a_{n}x^{n}$ — многочлен с целыми коэффициентами такой, что $\alpha$ это $k$ -й корень многочлена, где корни сортируются по абсолютному значению от меньшего к большему, а затем сортируются по аргументу от меньшего к большему. Мы можем определить функцию инъекции (т.е. взаимно-однозначную) $f:\mathbb {A} \to \mathbb {Q}$ данный $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ , где $p_{n}$ это $n$ -е простое число .

[30] Доказательство: Если $A_{i}$ является счетным множеством для каждого $i$ в $I=\{1,\dots ,n\}$ , то для каждого $i$ существует сюръективная функция $g_{i}:\mathbb {N} \to A_{i}$ и, следовательно, функция $G:I\times \mathbf {N} \to \bigcup _{i\in I}A_{i},$ данный $G(i,m)=g_{i}(m)$ это сюръективность. С $I\times \mathbb {N}$ счетно, объединение ${\textstyle \bigcup _{i\in I}A_{i}}$ является счетным.

[32] Доказательство : Как и в конечном случае, но $I=\mathbb {N}$ и мы используем аксиому счетного выбора, чтобы выбрать для каждого $i$ в $\mathbb {N}$ сюръекция $g_{i}$ из непустой совокупности сюръекций из $\mathbb {N}$ к $A_{i}$ . ^[26] Заметим, что поскольку мы рассматриваем сюръекцию $G:\mathbf {N} \times \mathbf {N} \to \bigcup _{i\in I}A_{i}$ , а не инъекции, нет требования, чтобы множества были непересекающимися.

[33] Доказательство : для (1) заметим, что если $T$ счетно, существует инъективная функция $h:T\to \mathbb {N}$ . Тогда, если $f:S\to T$ инъективен состав $h\circ f:S\to \mathbb {N}$ является инъективным, поэтому $S$ является счетным. Для (2) заметим, что если $S$ счетно либо $S$ пусто или существует сюръективная функция $h:\mathbb {N} \to S$ . Тогда, если $g:S\to T$ является сюръективным либо $S$ и $T$ оба пусты, или композиция $g\circ h:\mathbb {N} \to T$ является сюръективным. В любом случае $T$ является счетным.

[34] См. первое доказательство несчетности Кантора , а также свойство конечного пересечения # Приложения для топологического доказательства.

[2] Манетти, Марко (19 июня 2015 г.). Топология . Спрингер. п. 26. ISBN 978-3-319-16958-3 .

[Rudin-3] Рудин 1976 , Глава 2

[4] Люди 2016 , с. 181

[5] Камке 1950 , с. 2

[Lang-6] Перейти обратно: ^а ^б Ланг 1993 , §2 главы I

[Apostol-7] Апостол 1969 , с. 23, глава 1.14

[8] Тьерри, Виалар (4 апреля 2017 г.). Справочник по математике . Совет директоров - Книги по запросу. п. 24. ISBN 978-2-9551990-1-5 .

[9] Мукерджи, Субир Кумар (2009). Первый курс реального анализа . Академические издательства. п. 22. ISBN 978-81-89781-90-3 .

[Yaqub-10] Перейти обратно: ^а ^б ^с Якуб, Аладдин М. (24 октября 2014 г.). Введение в металогику . Бродвью Пресс. ISBN 978-1-4604-0244-3 .

[Singh-11] Сингх, Тедж Бахадур (17 мая 2019 г.). Введение в топологию . Спрингер. п. 422. ИСБН 978-981-13-6954-4 .

[Katzourakis-12] Перейти обратно: ^а ^б Кацуракис, Николаос; Варварука, Евгений (2 января 2018 г.). Наглядное введение в современный анализ . ЦРК Пресс. ISBN 978-1-351-76532-9 .

[13] Халмош 1960 , с. 91

[14] Камке 1950 , с. 2

[15] Длаб, Властимил; Уильямс, Кеннет С. (9 июня 2020 г.). Приглашение к алгебре: сборник ресурсов для учителей, студентов старших курсов и аспирантов по математике . Всемирная научная. п. 8. ISBN 978-981-12-1999-3 .

[16] Люди 2016 , с. 182

[17] Стиллвелл, Джон К. (2010), Дороги к бесконечности: математика истины и доказательства , CRC Press, стр. 10, ISBN 9781439865507 Открытие Кантором бесчисленных множеств в 1874 году было одним из самых неожиданных событий в истории математики. До 1874 года большинство людей даже не считали бесконечность законным математическим предметом, поэтому необходимость различать счетную и несчетную бесконечность не могла быть и вообразима.

[18] Кантор 1878, с. 242.

[19] Феррейрос 2007, стр. 268, 272–273.

[20] «Что такое наборы и форма состава?» . экспии . 09.05.2021. Архивировано из оригинала 18 сентября 2020 г.

[21] Халмош 1960 , с. 91

[22] Халмош 1960 , с. 92

[23] Авельсгаард 1990 , с. 182

[26] Камке 1950 , с. 3–4

[28] Авельсгаард 1990 , с. 180

[29] Флетчер и Пэтти 1988 , с. 187

[31] Хрбачек, Карел; Джех, Томас (22 июня 1999 г.). Введение в теорию множеств, третье издание, переработанное и расширенное . ЦРК Пресс. п. 141. ИСБН 978-0-8247-7915-3 .

[а]

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[б]

[с]

[23]

[д]

[24]

[25]

[Это]

[ф]

[г]

[час]

[22]

[26]

v т Это счисления Системы
Sets of definable numbers	Natural numbers ( $\mathbb {N}$ ) Integers ( $\mathbb {Z}$ ) Rational numbers ( $\mathbb {Q}$ ) Constructible numbers Algebraic numbers ( $\mathbb {A}$ ) Closed-form numbers Periods Computable numbers Arithmetical numbers Set-theoretically definable numbers Gaussian integers
Composition algebras	Division algebras: Real numbers ( $\mathbb {R}$ ) Complex numbers ( $\mathbb {C}$ ) Quaternions ( $\mathbb {H}$ ) Octonions ( $\mathbb {O}$ )
Split types	Over $\mathbb {R}$ : Split-complex numbers Split-quaternions Split-octonions Over $\mathbb {C}$ : Bicomplex numbers Biquaternions Bioctonions
Other hypercomplex	Dual numbers Dual quaternions Dual-complex numbers Hyperbolic quaternions Sedenions ( $\mathbb {S}$ ) Split-biquaternions Multicomplex numbers Geometric algebra/Clifford algebra Algebra of physical space Spacetime algebra Plane-based geometric algebra
Other types	Cardinal numbers Extended natural numbers Irrational numbers Fuzzy numbers Hyperreal numbers Levi-Civita field Surreal numbers Transcendental numbers Ordinal numbers p-adic numbers (p-adic solenoids) Supernatural numbers Profinite integers Superreal numbers Normal numbers
Classification List

v т Это Теория множеств
Overview	Set (mathematics)
Axioms	Adjunction Choice countable dependent global Constructibility (V=L) Determinacy Extensionality Infinity Limitation of size Pairing Power set Regularity Union Martin's axiom Axiom schema replacement specification
Operations	Cartesian product Complement (i.e. set difference) De Morgan's laws Disjoint union Identities Intersection Power set Symmetric difference Union
Concepts Methods	Almost Cardinality Cardinal number (large) Class Constructible universe Continuum hypothesis Diagonal argument Element ordered pair tuple Family Forcing One-to-one correspondence Ordinal number Set-builder notation Transfinite induction Venn diagram
Set types	Amorphous Countable Empty Finite (hereditarily) Filter base subbase Ultrafilter Fuzzy Infinite (Dedekind-infinite) Recursive Singleton Subset · Superset Transitive Uncountable Universal
Theories	Alternative Axiomatic Naive Cantor's theorem Zermelo General Principia Mathematica New Foundations Zermelo–Fraenkel von Neumann–Bernays–Gödel Morse–Kelley Kripke–Platek Tarski–Grothendieck
Paradoxes Problems	Russell's paradox Suslin's problem Burali-Forti paradox
Set theorists	Paul Bernays Georg Cantor Paul Cohen Richard Dedekind Abraham Fraenkel Kurt Gödel Thomas Jech John von Neumann Willard Quine Bertrand Russell Thoralf Skolem Ernst Zermelo