система Гильберта

В математической физике система Гильберта — нечасто используемый термин для обозначения физической системы, описываемой C*-алгеброй .

В логике , особенно в математической логике , система Гильберта , иногда называемая исчислением Гильберта , дедуктивной системой в стиле Гильберта или системой Гильберта-Акермана , представляет собой тип системы формальной дедукции , приписываемой Готлобу Фреге. и Дэвид Гилберт . Эти дедуктивные системы чаще всего изучаются для логики первого порядка , но представляют интерес и для других логик.

Большинство вариантов систем Гильберта придерживаются характерного подхода, балансируя между логическими аксиомами и правилами вывода . Гильбертовы системы могут характеризоваться выбором большого числа схем логических аксиом и небольшого набора правил вывода . Системы естественной дедукции придерживаются противоположного подхода, включая множество правил дедукции, но очень мало схем аксиом или вообще их отсутствие. Наиболее часто изучаемые системы Гильберта имеют либо только одно правило вывода – modus ponens для логики высказываний – либо два – с обобщением , а также для обработки логики предикатов – и несколько бесконечных схем аксиом. Системы Гильберта для алетических модальных логик , иногда называемые системами Гильберта-Льюиса , дополнительно требуют правила необходимости . Некоторые системы используют в качестве аксиом конечный список конкретных формул вместо бесконечного набора формул через схемы аксиом, и в этом случае равномерное правило замены требуется .

Характерной особенностью многих вариантов систем Гильберта является то, что контекст не изменяется ни в одном из их правил вывода, в то время как как естественная дедукция , так и секвенциальное исчисление содержат некоторые правила изменения контекста. Таким образом, если нас интересует только выводимость тавтологий , а не гипотетических суждений, то можно формализовать систему Гильберта так, чтобы ее правила вывода содержали только суждения довольно простой формы. То же самое нельзя сделать и с двумя другими системами вычетов: поскольку в некоторых из их правил вывода изменяется контекст, их нельзя формализовать, чтобы можно было избежать гипотетических суждений – даже если мы хотим использовать их только для доказательства выводимости тавтологии.

Формальные

A graphic representation of the deduction system

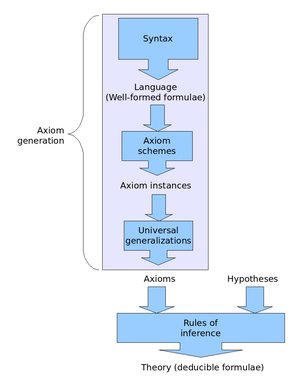
В системе вывода в стиле Гильберта формальный вывод представляет собой конечную последовательность формул, в которой каждая формула является либо аксиомой, либо получается из предыдущих формул по правилу вывода. Эти формальные выводы призваны отражать доказательства на естественном языке, хотя они гораздо более подробны.

Предполагать $\Gamma$представляет собой набор формул, рассматриваемых как гипотезы . Например, $\Gamma$может быть набором аксиом теории групп или теории множеств . Обозначения $\Gamma \vdash \phi$ означает, что существует вычет, который заканчивается $\phi$ используя в качестве аксиом только логические аксиомы и элементы $\Gamma$. Таким образом, неофициально $\Gamma \vdash \phi$ Значит это $\phi$ доказуемо, если принять все формулы из $\Gamma$.

Для систем дедукции в стиле Гильберта характерно использование многочисленных схем логических аксиом . Схема аксиом — это бесконечный набор аксиом, полученный путем подстановки всех формул той или иной формы в определенный шаблон. Набор логических аксиом включает в себя не только аксиомы, порожденные этим шаблоном, но и любое обобщение одной из этих аксиом. Обобщение формулы получается путем добавления к формуле нуля или более кванторов универсальности; например $\forall y(\forall xPxy\to Pty)$ представляет собой обобщение $\forall xPxy\to Pty$.

Логические аксиомы

Существует несколько вариантов аксиоматизации логики предикатов, поскольку для любой логики существует свобода выбора аксиом и правил, характеризующих эту логику. Здесь мы описываем систему Гильберта с девятью аксиомами и только modus ponens, которую мы называем аксиоматизацией с одним правилом и которая описывает классическую эквациональную логику. Мы имеем дело с минимальным языком этой логики, где в формулах используются только связки $\lnot$ и $\to$ и только квантификатор $\forall$. Позже мы покажем, как можно расширить систему, включив в нее дополнительные логические связки, такие как $\land$ и $\lor$, не расширяя класс выводимых формул.

Первые четыре схемы логических аксиом позволяют (вместе с modus ponens) манипулировать логическими связками.

П1. $\phi \to \phi$

П2. $\phi \to \left(\psi \to \phi \right)$

П3. $\left(\phi \to \left(\psi \rightarrow \xi \right)\right)\to \left(\left(\phi \to \psi \right)\to \left(\phi \to \xi \right)\right)$

П4. $\left(\lnot \phi \to \lnot \psi \right)\to \left(\psi \to \phi \right)$

Аксиома P1 избыточна, как это следует из P3, P2 и modus ponens (см. доказательство ). Эти аксиомы описывают классическую логику высказываний ; без аксиомы P4 мы получаем положительную импликационную логику . Минимальная логика достигается либо добавлением вместо аксиомы P4m, либо определением $\lnot \phi$ как $\phi \to \bot$.

П4м. $\left(\phi \to \psi \right)\to \left(\left(\phi \to \lnot \psi \right)\to \lnot \phi \right)$

Интуиционистская логика достигается добавлением аксиом P4i и P5i к позитивной импликационной логике или добавлением аксиомы P5i к минимальной логике. И P4i, и P5i являются теоремами классической логики высказываний.

P4i. $\left(\phi \to \lnot \phi \right)\to \lnot \phi$

П5и. $\lnot \phi \to \left(\phi \to \psi \right)$

Обратите внимание, что это схемы аксиом, которые представляют бесконечное множество конкретных случаев аксиом. Например, P1 может представлять конкретный экземпляр аксиомы. $p\to p$, или это может представлять $\left(p\to q\right)\to \left(p\to q\right)$: $\phi$это место, куда можно поместить любую формулу. Такая переменная, которая варьируется по формулам, называется «схематической переменной».

С помощью второго правила равномерной замены (US) мы можем превратить каждую из этих схем аксиом в одну аксиому, заменив каждую схематическую переменную некоторой пропозициональной переменной, которая не упоминается ни в одной аксиоме, чтобы получить то, что мы называем замещающей аксиоматизацией. Обе формализации имеют переменные, но там, где аксиоматизация с одним правилом имеет схематические переменные, находящиеся за пределами языка логики, замещающая аксиоматизация использует пропозициональные переменные, которые выполняют ту же работу, выражая идею переменной, распространяющейся по формулам с правилом, использующим замену.

НАС. Позволять $\phi (p)$ быть формулой с одним или несколькими экземплярами пропозициональной переменной $p$, и разреши $\psi$быть другая формула. Затем из $\phi (p)$, сделать вывод $\phi (\psi )$.

Следующие три схемы логических аксиом предоставляют способы добавления, манипулирования и удаления кванторов универсальности.

Вопрос 5. $\forall x\left(\phi \right)\to \phi [x:=t]$ где t может быть заменено на x в $\,\!\phi$

Вопрос 6. $\forall x\left(\phi \to \psi \right)\to \left(\forall x\left(\phi \right)\to \forall x\left(\psi \right)\right)$

Вопрос 7. $\phi \to \forall x\left(\phi \right)$ где x не свободен в $\phi$.

Эти три дополнительных правила расширяют систему высказываний, чтобы аксиоматизировать классическую логику предикатов . Аналогично, эти три правила расширяют систему интуиционистской логики высказываний (с P1-3, P4i и P5i) до интуиционистской логики предикатов .

Универсальная квантификация часто дается альтернативной аксиоматизацией с использованием дополнительного правила обобщения (см. раздел «Метатеоремы»), и в этом случае правила Q6 и Q7 излишни.

Окончательные схемы аксиом необходимы для работы с формулами, содержащими символ равенства.

И8. $x=x$ для каждой переменной x .

И9. $\left(x=y\right)\to \left(\phi [z:=x]\to \phi [z:=y]\right)$

Консервативные

В систему дедукции в стиле Гильберта обычно включаются только аксиомы импликации и отрицания. Учитывая эти аксиомы, можно сформировать консервативные расширения теоремы о дедукции , допускающие использование дополнительных связок. Эти расширения называются консервативными, потому что если формула φ, включающая новые связки, переписана как логически эквивалентная формула θ, включающая только отрицание, импликацию и универсальную квантификацию, то φ выводима в расширенной системе тогда и только тогда, когда θ выводима в исходной системе. . В полном расширении система в стиле Гильберта будет больше напоминать систему естественной дедукции .

Экзистенциальная

• Введение

$\forall x(\phi \to \exists y(\phi [x:=y]))$

• Устранение

$\forall x(\phi \to \psi )\to \exists x(\phi )\to \psi$ где $x$ не является свободной переменной $\psi$.

Соединение и дизъюнкция

• Введение и устранение союза

введение: $\alpha \to (\beta \to \alpha \land \beta )$

удаление осталось: $\alpha \wedge \beta \to \alpha$

право на удаление: $\alpha \wedge \beta \to \beta$

• Введение и устранение дизъюнкции

вступление осталось: $\alpha \to \alpha \vee \beta$

введение справа: $\beta \to \alpha \vee \beta$

устранение: $(\alpha \to \gamma )\to ((\beta \to \gamma )\to \alpha \vee \beta \to \gamma )$

Метатеоремы

Поскольку в системах в стиле Гильберта очень мало правил дедукции, обычно доказываются метатеоремы , которые показывают, что дополнительные правила дедукции не добавляют дедуктивной силы в том смысле, что дедукция, использующая новые правила дедукции, может быть преобразована в дедукцию, используя только исходную дедукцию. правила.

Некоторые распространенные метатеоремы этой формы:

• Теорема о дедукции : $\Gamma ;\phi \vdash \psi$ если и только если $\Gamma \vdash \phi \to \psi$.
• $\Gamma \vdash \phi \leftrightarrow \psi$ если и только если $\Gamma \vdash \phi \to \psi$ и $\Gamma \vdash \psi \to \phi$.
• Противопоставление: Если $\Gamma ;\phi \vdash \psi$ затем $\Gamma ;\lnot \psi \vdash \lnot \phi$.
• Обобщение : если $\Gamma \vdash \phi$ и x не встречается в свободном виде ни в одной формуле $\Gamma$ затем $\Gamma \vdash \forall x\phi$.

Некоторые полезные теоремы и их доказательства

Ниже приведены несколько теорем логики высказываний, а также их доказательства (или ссылки на эти доказательства в других статьях). Обратите внимание: поскольку (P1) само по себе можно доказать, используя другие аксиомы, фактически (P2), (P3) и (P4) достаточно для доказательства всех этих теорем.

(HS1) $(q\to r)\to ((p\to q)\to (p\to r))$ - Гипотетический силлогизм , см. доказательство .

(Л1) $p\to ((p\to q)\to q)$ - доказательство:

(1) $((p\to q)\to (p\to q))\to (((p\to q)\to p)\to ((p\to q)\to q))$ (пример (P3))

(2) $(p\to q)\to (p\to q)$ (пример (P1))

(3) $((p\to q)\to p)\to ((p\to q)\to q)$ (из (2) и (1) в режиме настройки )

(4) $(((p\to q)\to p)\to ((p\to q)\to q))\to ((p\to ((p\to q)\to p))\to (p\to ((p\to q)\to q)))$ (пример (HS1))

(5) $(p\to ((p\to q)\to p))\to (p\to ((p\to q)\to q))$ (из (3) и (4) методом настройки)

(6) $p\to ((p\to q)\to p)$ (пример (P2))

(7) $p\to ((p\to q)\to q)$ (из (6) и (5) методом настройки)

Следующие две теоремы вместе известны как двойное отрицание :

(ДН1) $\neg \neg p\to p$

(ДН2) $p\to \neg \neg p$

Смотрите доказательства .

(Л2) $(p\to (q\to r))\to (q\to (p\to r))$ - для этого доказательства мы используем метод метатеоремы гипотетического силлогизма как сокращение для нескольких шагов доказательства:

(1) $(p\to (q\to r))\to ((p\to q)\to (p\to r))$ (пример (P3))

(2) $((p\to q)\to (p\to r))\to ((q\to (p\to q))\to (q\to (p\to r)))$ (пример (HS1))

(3) $(p\to (q\to r))\to ((q\to (p\to q))\to (q\to (p\to r)))$ (из (1) и (2) с использованием метатеоремы гипотетического силлогизма)

(4) $((p\to (q\to r))\to ((q\to (p\to q))\to (q\to (p\to r))))\to (((p\to (q\to r))\to (q\to (p\to q)))\to ((p\to (q\to r))\to (q\to (p\to r))))$ (пример (P3))

(5) $((p\to (q\to r))\to (q\to (p\to q)))\to ((p\to (q\to r))\to (q\to (p\to r)))$ (из (3) и (4) с использованием modus ponens)

(6) $q\to (p\to q)$ (пример (P2))

(7) $(q\to (p\to q))\to ((p\to (q\to r))\to (q\to (p\to q)))$ (пример (P2))

(8) $(p\to (q\to r))\to (q\to (p\to q))$ (из (6) и (7) с использованием modus ponens)

(9) $(p\to (q\to r))\to (q\to (p\to r))$ (из (8) и (5) с использованием modus ponens)

(HS2) $(p\to q)\to ((q\to r)\to (p\to r))$— альтернативная форма гипотетического силлогизма . доказательство:

(1) $(q\to r)\to ((p\to q)\to (p\to r))$ (пример (HS1))

(2) $((q\to r)\to ((p\to q)\to (p\to r)))\to ((p\to q)\to ((q\to r)\to (p\to r)))$ (пример (L2))

(3) $(p\to q)\to ((q\to r)\to (p\to r))$ (из (1) и (2) методом настройки)

(ТР1) $(p\to q)\to (\neg q\to \neg p)$ - Транспонирование, см. доказательство (другое направление транспонирования — (P4)).

(ТР2) $(\neg p\to q)\to (\neg q\to p)$- другая форма транспозиции; доказательство:

(1) $(\neg p\to q)\to (\neg q\to \neg \neg p)$ (экземпляр (TR1))

(2) $\neg \neg p\to p$ (экземпляр (DN1))

(3) $(\neg \neg p\to p)\to ((\neg q\to \neg \neg p)\to (\neg q\to p))$ (пример (HS1))

(4) $(\neg q\to \neg \neg p)\to (\neg q\to p)$ (из (2) и (3) методом настройки)

(5) $(\neg p\to q)\to (\neg q\to p)$ (из (1) и (4) с использованием метатеоремы гипотетического силлогизма)

(Л3) $(\neg p\to p)\to p$ - доказательство:

(1) $\neg p\to (\neg \neg (q\to q)\to \neg p)$ (пример (P2))

(2) $(\neg \neg (q\to q)\to \neg p)\to (p\to \neg (q\to q))$ (пример (P4))

(3) $\neg p\to (p\to \neg (q\to q))$ (из (1) и (2) с использованием метатеоремы гипотетического силлогизма)

(4) $(\neg p\to (p\to \neg (q\to q)))\to ((\neg p\to p)\to (\neg p\to \neg (q\to q)))$ (пример (P3))

(5) $(\neg p\to p)\to (\neg p\to \neg (q\to q))$ (из (3) и (4) с использованием мод ponens)

(6) $(\neg p\to \neg (q\to q))\to ((q\to q)\to p)$ (пример (P4))

(7) $(\neg p\to p)\to ((q\to q)\to p)$ (из (5) и (6) с использованием метатеоремы гипотетического силлогизма)

(8) $q\to q$ (пример (P1))

(9) $(q\to q)\to (((q\to q)\to p)\to p)$ (пример (L1))

(10) $((q\to q)\to p)\to p$ (из (8) и (9) с использованием мод ponens)

(11) $(\neg p\to p)\to p$ (из (7) и (10) с использованием метатеоремы гипотетического силлогизма)

Альтернативные аксиоматизации

Дополнительная информация: Список логических систем.

Приведенная выше аксиома 3 принадлежит Лукасевичу . В исходной системе Фреге были аксиомы P2 и P3, но вместо аксиомы P4 были еще четыре аксиомы (см. Исчисление высказываний Фреге ). Рассел и Уайтхед также предложили систему с пятью пропозициональными аксиомами.

Дальнейшие связи

Аксиомы P1, P2 и P3 с modus ponens правила вывода (формализующие интуиционистскую логику высказываний ) соответствуют комбинаторной логики базовым комбинаторам I , K и S с оператором приложения. Доказательства в системе Гильберта тогда соответствуют комбинаторным членам комбинаторной логики. См. также переписку Карри-Ховарда .

См. также

• Список систем Гильберта
• Естественный вычет

Ссылки

• Карри, Хаскелл Б.; Роберт Фейс (1958). Комбинаторная логика Vol. Я. ​ Том. 1. Амстердам: Северная Голландия.
• Монк, Дж. Дональд (1976). Математическая логика . Тексты для аспирантов по математике. Берлин, Нью-Йорк: Springer-Verlag . ISBN  978-0-387-90170-1 .
• Ружа, Имре; Мате, Андраш (1997). Введение в современную логику (на венгерском языке). Будапешт: Издательство Осирис.
• Тарский, Альфред (1990). Доказательство и правда (на венгерском языке). Будапешт: Мысль. Это венгерский перевод Альфреда Тарского избранных статей по семантической теории истины .
• Дэвид Гильберт (1927) «Основы математики», перевод Стефана Бауэра-Менглерберга и Дагфинна Фёллесдала (стр. 464–479). в:
  • ван Хейеноорт, Жан (1967). От Фреге до Гёделя: Справочник по математической логике, 1879–1931 (3-е издание, 1976 г.). Кембридж, Массачусетс: Издательство Гарвардского университета. ISBN  0-674-32449-8 .
  • В книге Гильберта 1927 года, основанной на более ранней лекции «Основы» 1925 года (стр. 367–392), представлены его 17 аксиом - аксиомы импликации № 1–4, аксиомы о & и V № 5–10, аксиомы отрицания № 11- 12, его логическая ε-аксиома № 13, аксиомы равенства № 14–15 и аксиомы № 16–17, а также другие необходимые элементы его формалистической «теории доказательства» – например, аксиомы индукции, аксиомы рекурсии, и т. д; он также предлагает энергичную защиту против интуиционизма Л. Дж. Брауэра. См. также комментарии и опровержения Германа Вейля (1927) (стр. 480–484), приложение Пола Бернея (1927) к лекции Гильберта (стр. 485–489) и ответ Луицена Эгбертуса Яна Брауэра (1927) (стр. 490–495).
• Клини, Стивен Коул (1952). Введение в метаматематику (10-е издание с исправлениями 1971 г., изд.). Амстердам, штат Нью-Йорк: Издательская компания Северной Голландии. ISBN  0-7204-2103-9 .
  • См., в частности, главу IV «Формальная система» (стр. 69–85), в которой Клини представляет подразделы §16 Формальные символы, §17 Правила формирования, §18 Свободные и связанные переменные (включая замену), §19 Правила преобразования (например, modus ponens) — и из них он представляет 21 «постулат» — 18 аксиом и 3 отношения «непосредственных последствий», разделенных следующим образом: Постулаты для исчисления высказываний № 1–8, Дополнительные постулаты для исчисления предикатов № 9–12 и Дополнительные постулаты для исчисления высказываний № 9–12 и Дополнительные постулаты для исчисления высказываний № 9–12. теория чисел № 13-21.

Внешние ссылки

• Гейфман, Хаим. «Дедуктивная система типа Гильберта для логики предложений, полноты и компактности» (PDF) .
• Фармер, В.М. «Пропозициональная логика» (PDF) . Он описывает (среди прочего) часть системы дедукции в стиле Гильберта (ограниченной исчислением высказываний ).