Пропозициональное исчисление

Не путать с пропозициональным анализом .

Пропозициональное исчисление это раздел логики . Ее еще называют логикой высказываний . логика высказываний , предложений исчисление сентенциальная логика , или иногда логика нулевого порядка . Речь идет о предложениях (что может быть правдой или ложью ) и отношения между предложениями, включая построение аргументов на их основе. Сложные предложения образуются путем соединения предложений логическими связками, истинностные функции конъюнкции представляющими , дизъюнкции , импликации , двуусловия и отрицания . Некоторые источники включают другие связки, как показано в таблице ниже.

В отличие от логики первого порядка , логика высказываний не имеет дело с нелогическими объектами, предикатами о них или кванторами . Однако весь механизм логики высказываний включен в логику первого порядка и логику высшего порядка. В этом смысле логика высказываний является основой логики первого порядка и логики высшего порядка.

Логика высказываний обычно изучается с помощью формального языка, на котором предложения представлены буквами, которые называются пропозициональными переменными . Затем они используются вместе с символами связок для образования сложных предложений. В связи с этим пропозициональные переменные называются атомарными формулами формального языка нулевого порядка. Хотя атомарные предложения обычно представляются буквами алфавита, существует множество обозначений для обозначения логических связок. В следующей таблице показаны основные варианты обозначений каждой из связок в логике высказываний.

Нотационные варианты связок

соединительный	Символ
И	$A\land B$, $A\cdot B$, $AB$, $A\&B$, $A\&\&B$
эквивалент	$A\equiv B$, $A\Leftrightarrow B$, $A\leftrightharpoons B$
подразумевает	$A\Rightarrow B$, $A\supset B$, $A\rightarrow B$
NAND	$A{\overline {\land }}B$, $A\mid B$, ${\overline {A\cdot B}}$
неэквивалентный	$A\not \equiv B$, $A\not \Leftrightarrow B$, $A\nleftrightarrow B$
НИ	$A{\overline {\lor }}B$, $A\downarrow B$, ${\overline {A+B}}$
НЕТ	$\neg A$, $-A$, ${\overline {A}}$, $\sim A$
ИЛИ	$A\lor B$, $A+B$, $A\mid B$, $A\parallel B$
ИСНО-ИЛИ	$A$ ИСНО-ИЛИ $B$
БЕСПЛАТНО	$A{\underline {\lor }}B$, $A\oplus B$

Наиболее тщательно исследованной ветвью логики высказываний является классическая функционально-истинная логика высказываний . в котором формулы интерпретируются как имеющие ровно одно из двух возможных значений истинности : истинностное значение true или истинностное значение false . принцип бивалентности и закон исключенного третьего Поддерживается . По сравнению с логикой первого порядка , истинностно-функциональная логика высказываний считается логикой нулевого порядка .

История

Основная статья: История логики

Хотя на логику высказываний (также называемую исчислением высказываний) намекали более ранние философы, она была развита в формальную логику ( стоическую логику ) Хрисиппом в III веке до нашей эры. и расширен его преемниками стоиками . Логика была сосредоточена на предложениях . Это отличалось от традиционной силлогистической логики , которая фокусировалась на терминах . Однако большая часть оригинальных сочинений была утеряна. и где-то между III и VI веками нашей эры стоическая логика ушла в небытие и возродилась только в XX веке, после (повторного) открытия пропозициональной логики.

Символическая логика , которая стала важной для уточнения логики высказываний, была впервые разработана математиком 17-18 веков Готфридом Лейбницем , чей логический алгоритм был, однако, неизвестен более широкому логическому сообществу. Следовательно, многие достижения Лейбница были воссозданы логиками, такими как Джордж Буль и Огастес Де Морган , совершенно независимыми от Лейбница.

Готтлоба Фреге Логика предикатов основана на логике высказываний и описывается как сочетание «отличительных черт силлогистической логики и логики высказываний». Следовательно, логика предикатов открыла новую эру в истории логики; однако прогресс в логике высказываний все еще был достигнут после Фреге, включая естественную дедукцию , деревья истинности и таблицы истинности . Естественная дедукция была изобретена Герхардом Генценом и Станиславом Ясковским . Деревья истины были изобретены Эвертом Виллемом Бетом . Однако изобретение таблиц истинности имеет неясную причину.

В произведениях Фреге и Бертран Рассел , — идеи, повлиявшие на изобретение таблиц истинности. Фактическая табличная структура (отформатированная в виде таблицы) обычно приписывается либо Людвигу Витгенштейну , либо Эмилю Посту (или обоим, независимо). Помимо Фреге и Рассела, другие авторы идей, предшествующих таблицам истинности, включают Филона, Буля, Чарльза Сандерса Пирса , и Эрнст Шредер . Табличную структуру приписывают Яну Лукасевичу , Альфреду Норту Уайтхеду , Уильяму Стэнли Джевонсу , Джону Венну и Кларенсу Ирвингу Льюису . В конце концов, некоторые, как Джон Шоски, пришли к выводу, что «далеко не очевидно, что какому-то одному человеку следует давать титул «изобретателя» таблиц истинности».

Предложения

Основная статья: Предложение

Логика высказываний, изучаемая в настоящее время в университетах, представляет собой спецификацию стандарта логического следования , в котором только значения пропозициональных связок учитываются при оценке условий истинности предложения или того, следует ли предложение логически из какого-либо другого предложения или группа предложений.

Повествовательные предложения

Пропозициональная логика имеет дело с утверждениями , которые определяются как повествовательные предложения, имеющие истинностное значение. Примеры заявлений могут включать:

• Википедия — бесплатная онлайн-энциклопедия, которую может редактировать каждый.
• Лондон - столица Англии .
• Все редакторы Википедии говорят как минимум на трех языках .

Повествовательным предложениям противопоставляются вопросы , такие как «Что такое Википедия?», и повелительные утверждения, такие как «Пожалуйста, добавьте цитаты , подтверждающие утверждения в этой статье». Такие недекларативные предложения не имеют истинностного значения . и рассматриваются только в неклассической логике , называемой эротетической и императивной логикой .

Соединение предложений с помощью связок

См. Также: Атомная формула и Атомное предложение.

В пропозициональной логике утверждение может содержать в качестве частей одно или несколько других утверждений. Сложные предложения образуются из более простых предложений и выражают отношения между составными предложениями. Это делается путем объединения их логическими связками : Основными типами сложных предложений являются отрицания , союзы , дизъюнкции , импликации и двуусловные предложения . которые образуются с помощью соответствующих связок для соединения предложений. В английском языке эти связки выражаются словами «и» ( конъюнкция ), «или» ( дизъюнкция ), «не» ( отрицание ), «if» ( материальный условный ), «if и only if» ( двуусловный ). Примерами таких сложных предложений могут быть:

• Википедия — это бесплатная онлайн-энциклопедия, которую может редактировать каждый, и миллионы людей уже имеют файлы . (соединение)
• Неправда, что все редакторы Википедии говорят как минимум на трех языках. (отрицание)
• Либо Лондон — столица Англии, либо Лондон — столица Соединенного Королевства , либо и то, и другое. (дизъюнкция)

Если в предложениях отсутствуют логические связки, их называют простыми предложениями . или атомарные предложения ; если они содержат одну или несколько логических связок, они называются сложными предложениями , или молекулярные предложения .

Сентенциальные связки — это более широкая категория, включающая логические связки. Сентенциальные связки – это любые лингвистические частицы, которые связывают предложения, образуя новое сложное предложение. или которые изменяют одно предложение, чтобы создать новое предложение. Логическая связка , или пропозициональная связка , — это разновидность пропозициональной связки с характерной особенностью, заключающейся в том, что, когда исходные предложения, над которыми она действует, являются (или выражают) предложениями , новое предложение, возникающее в результате ее применения, также является (или выражает) предложением . . Философы расходятся во мнениях относительно того, что именно представляет собой предложение. а также о том, какие промысловые связки в естественных языках следует считать логическими связками. Сентенциальные связки еще называют функторами предложений . а логические связки также называются функторами истинности .

Аргументы

Основная статья: Аргумент

Аргумент . определяется как пара вещей, а именно набор предложений, посылками называемых и предложение, называемое заключением . Утверждается, что вывод следует из посылок, и утверждается, что предпосылки подтверждают этот вывод.

Пример аргумента

Ниже приводится пример аргумента в рамках пропозициональной логики:

Посылка 1: Если идет дождь, то облачно.

Предпосылка 2: Идет дождь.

Вывод: облачно.

Логическая форма этого аргумента известна как modus ponens . что является классически допустимой формой. Итак, в классической логике аргумент действителен , хотя он может быть или не быть здравым , в зависимости от метеорологических фактов в данном контексте. Этот пример аргумента будет повторно использоваться при объяснении § Формализации .

Валидность и обоснованность

Основные статьи: Валидность (логика) и обоснованность

Аргумент действителен тогда и только тогда, когда необходимо , чтобы все его посылки истинны, а его вывод был истинным. Альтернативно, аргумент действителен тогда и только тогда, когда невозможно, чтобы все посылки были истинными, а заключение ложно.

Валидность противопоставляется обоснованности . Аргумент является обоснованным тогда и только тогда, когда он действителен и все его посылки верны. В противном случае это неразумно .

Логика, как правило, стремится точно указать действительные аргументы. Это делается путем определения валидного аргумента как аргумента, вывод которого является логическим следствием его посылок. что, когда это понимается как семантическое следствие , означает, что не существует случая , в котором посылки истинны, но вывод неверен. – см. § Семантика ниже.

Формализация

Пропозициональная логика обычно изучается посредством формальной системы в которой формулы формального языка интерпретируются , как представляющие предложения . Этот формальный язык является основой систем доказательств , которые позволяют сделать вывод из посылок тогда и только тогда, когда он является логическим следствием их . В этом разделе будет показано, как это работает, путем формализации аргумента § Пример . Формальный язык исчисления высказываний будет полностью определен в § Язык , а обзор систем доказательств будет дан в § Системы доказательств .

Пропозициональные переменные

Основная статья: Пропозициональная переменная

Поскольку логика высказываний не занимается структурой предложений за пределами той точки, где они больше не могут быть разложены логическими связками, его обычно изучают путем замены таких атомарных (неделимых) высказываний буквами алфавита, которые интерпретируются как переменные, представляющие высказывания ( пропозициональные переменные ). При использовании пропозициональных переменных аргумент § Пример будет тогда обозначен следующим образом:

Предпосылка 1: $P\to Q$

Предпосылка 2: $P$

Заключение: $Q$

Когда P интерпретируется как «Идет дождь», а Q как «облачно», эти символические выражения точно соответствуют исходному выражению на естественном языке. Мало того, они также будут соответствовать любому другому выводу той же логической формы .

Когда для представления формальной логики используется формальная система, используются только буквы утверждений (обычно заглавные латинские буквы, такие как $P$, $Q$ и $R$) представлены напрямую. Предложения естественного языка, возникающие при их интерпретации, находятся за пределами системы, и отношения между формальной системой и ее интерпретацией также находятся за пределами самой формальной системы.

Генценовские обозначения

Если мы предположим, что истинность modus ponens была принята как аксиома , то тот же аргумент § Примера также можно изобразить следующим образом:

${\frac {P\to Q,P}{Q}}$

Этот метод отображения представляет собой естественной обозначение Генцена для дедукции и секвенциального исчисления . Помещения показаны над линией, называемой линией вывода . разделяются запятой , что указывает на совмещение помещений. Заключение пишется под линией вывода. Линия вывода представляет синтаксическое следствие , иногда называют дедуктивным следствием , который также обозначается знаком ⊢. Таким образом, вышеизложенное также можно записать в одну строку как $P\to Q,P\vdash Q$.

Синтаксическое последствие противопоставляется семантическому последствию . который обозначается ⊧. В этом случае вывод следует синтаксически, поскольку естественное правило вывода modus ponens предполагается . Дополнительную информацию о правилах вывода см. в разделах, посвященных системам доказательств, ниже.

Язык

Язык называемый (обычно ${\mathcal {L}}$) Исчисление высказываний определяется в терминах:

1. набор примитивных символов, называемых атомарными формулами , атомарными предложениями , атомы, заполнители , простые формулы , буквы-предложения , буквы-предложения , или переменные , и
2. набор операторных символов, называемых связками , логические связи , логические операторы , истинностно-функциональные связки, функторы истинности , или пропозициональные связки .

— Правильно составленная формула это любая атомарная формула или любая формула, которая может быть составлена ​​из атомарных формул с помощью операторных символов в соответствии с правилами грамматики. Язык ${\mathcal {L}}$, то определяется либо как идентичное своему набору правильно построенных формул, или как содержащий этот набор (вместе, например, с набором связок и переменных).

Обычно синтаксис ${\mathcal {L}}$определяется рекурсивно всего несколькими определениями, как показано ниже; некоторые авторы явно включают круглые скобки в качестве знаков препинания при определении синтаксиса своего языка, в то время как другие используют их без комментариев.

Синтаксис

Учитывая набор атомарных пропозициональных переменных $p_{1}$, $p_{2}$, $p_{3}$, ..., и набор пропозициональных связок $c_{1}^{1}$, $c_{2}^{1}$, $c_{3}^{1}$, ..., $c_{1}^{2}$, $c_{2}^{2}$, $c_{3}^{2}$, ..., $c_{1}^{3}$, $c_{2}^{3}$, $c_{3}^{3}$, ..., формула логики высказываний определяется рекурсивно этими определениями:

Определение 1 : Атомарные пропозициональные переменные являются формулами.

Определение 2 : Если $c_{n}^{m}$ является пропозициональной связкой и $\langle$А, Б, В, … $\rangle$ представляет собой последовательность m, возможно, но не обязательно атомарных, возможно, но не обязательно различных формул, тогда результат применения $c_{n}^{m}$ чтобы к $\langle$А, Б, В, … $\rangle$ это формула.

Определение 3: Ничто иное не является формулой.

Написание результата применения $c_{n}^{m}$ к $\langle$А, Б, В, … $\rangle$ в функциональной записи, как $c_{n}^{m}$(A, B, C, …), в качестве примеров корректных формул мы имеем следующие:

• $p_{5}$
• $c_{3}^{2}(p_{2},p_{9})$
• $c_{3}^{2}(p_{1},c_{2}^{1}(p_{3}))$
• $c_{1}^{3}(p_{4},p_{6},c_{2}^{2}(p_{1},p_{2}))$
• $c_{4}^{2}(c_{1}^{1}(p_{7}),c_{3}^{1}(p_{8}))$
• $c_{2}^{3}(c_{1}^{2}(p_{3},p_{4}),c_{2}^{1}(p_{5}),c_{3}^{2}(p_{6},p_{7}))$
• $c_{3}^{1}(c_{1}^{3}(p_{2},p_{3},c_{2}^{2}(p_{4},p_{5})))$

То, что было дано выше как Определение 2 , отвечающее за композицию формул, Колин Хаусон называет принципом композиции . Именно эта рекурсия в определении синтаксиса языка оправдывает использование слова «атомарный» для обозначения пропозициональных переменных, поскольку все формулы в языке ${\mathcal {L}}$ состоят из атомов как основных строительных блоков. Сложные формулы (все формулы, кроме атомов) называются молекулами . или молекулярные предложения . (Это несовершенная аналогия с химией , поскольку химическая молекула иногда может иметь только один атом, как в одноатомных газах .)

Определение «ничто иное не является формулой», данное выше в виде определения 3 , исключает из языка любую формулу, которая конкретно не требуется другими определениями синтаксиса. В частности, это исключает бесконечно длинных формул правильность формирования .

Грамматика CF в BNF

Альтернативой приведенным выше определениям синтаксиса является написание контекстно-свободной (CF) грамматики для языка. ${\mathcal {L}}$ в форме Бэкуса-Наура (БНФ). Это чаще встречается в информатике, чем в философии . Это можно сделать разными способами, из которых особенно кратким для общего набора из пяти связок является это единственное предложение:

$\phi ::=a_{1},a_{2},\ldots ~|~\neg \phi ~|~\phi ~\&~\psi ~|~\phi \vee \psi ~|~\phi \rightarrow \psi ~|~\phi \leftrightarrow \psi$

Это предложение, в силу его самореферентного характера (поскольку $\phi$ есть в некоторых ответвлениях определения $\phi$), также действует как рекурсивное определение и, следовательно, определяет весь язык. Чтобы расширить его за счет добавления модальных операторов , нужно всего лишь добавить… $|~\Box \phi ~|~\Diamond \phi$ до конца пункта.

Константы и схемы

Математики иногда различают пропозициональные константы, пропозициональные переменные и схемы. Пропозициональные константы представляют собой некоторое частное предложение, в то время как пропозициональные переменные варьируются по множеству всех атомарных предложений. Однако схемы или схематические буквы встречаются во всех формулах. (Схематические буквы также называются метапеременными .) Обычно пропозициональные константы обозначаются буквами A , B и C , пропозициональные переменные — буквами P , Q и R , а схематические буквы часто представляют собой греческие буквы, чаще всего φ , ψ и χ .

Однако некоторые авторы признают в своей формальной системе только две «пропозициональные константы»: специальный символ $\top$, называемый «истина», который всегда имеет значение True , и специальный символ $\bot$, называемый «ложностью», который всегда имеет значение False . Другие авторы также включают эти символы с тем же значением, но считают их «функторами истинности с нулевым местом». или, что то же самое, « нульарные связки».

Семантика

Основные статьи: Семантика логики и теория моделей

Чтобы служить моделью логики данного естественного языка , формальный язык должен быть семантически интерпретирован. В классической логике все предложения оцениваются ровно в одно из двух истинностных значений : истинное или ложное . Например, « Википедия — это бесплатная онлайн-энциклопедия , которую может редактировать каждый» имеет значение True . в то время как «Википедия — это бумажная энциклопедия » оценивается как False .

В остальном к языку любой логики высказываний может быть применима следующая формальная семантика, но предположения о том, что существует только два семантических значения ( двухвалентность ), что каждой формуле в языке присвоено только одно из двух ( непротиворечие ), и то, что каждой формуле присваивается значение ( исключается среднее ), являются отличительными чертами классической логики. Чтобы узнать о неклассических логиках с более чем двумя истинностными значениями и их уникальной семантике, можно обратиться к статьям « Многозначная логика », « Трехзначная логика », « Конечнозначная логика » и « Бесконечнозначная логика ». логика ».

Интерпретация (случай) и аргумент

Основная статья: Интерпретация (логика)

Для данного языка ${\mathcal {L}}$, интерпретация , или случай , – это присвоение смысловых значений каждой формуле ${\mathcal {L}}$. Для формального языка классической логики случай определяется как присвоение каждой формуле ${\mathcal {L}}$, одного или другого, но не обоих, значений истинности , а именно истинности ( T или 1) и ложности ( F или 0). Интерпретация формального языка классической логики часто выражается в терминах таблиц истинности . Поскольку каждой формуле присваивается только одно истинностное значение, интерпретацию можно рассматривать как функцию , область определения которой равна ${\mathcal {L}}$, и чей диапазон представляет собой набор его семантических значений ${\mathcal {V}}=\{{\mathsf {T}},{\mathsf {F}}\}$, или ${\mathcal {V}}=\{1,0\}$.

Для $n$ существуют отдельные пропозициональные символы $2^{n}$различные возможные интерпретации. Для любого конкретного символа $a$, например, есть $2^{1}=2$ возможные интерпретации: либо $a$ присваивается T , или $a$присвоено Ф. ​ И для пары $a$, $b$ есть $2^{2}=4$ возможные интерпретации: либо обоим присвоено T , либо обоим присвоено F , либо $a$ присваивается T и $b$ присваивается F или $a$ присваивается F и $b$ присвоено Т. ​ С ${\mathcal {L}}$ имеет $\aleph _{0}$, то есть счетно много пропозициональных символов, существуют $2^{\aleph _{0}}={\mathfrak {c}}$, и, следовательно, бесчисленное множество различных возможных интерпретаций ${\mathcal {L}}$ в целом.

Где ${\mathcal {I}}$ представляет собой интерпретацию и $\varphi$ и $\psi$ представляют формулы, определение аргумента , данное в § Аргументы , может быть затем сформулировано как пара $\langle \{\varphi _{1},\varphi _{2},\varphi _{3},...,\varphi _{n}\},\psi \rangle$, где $\{\varphi _{1},\varphi _{2},\varphi _{3},...,\varphi _{n}\}$ представляет собой совокупность помещений и $\psi$это вывод. аргумента Определение достоверности , т.е. его свойства, которое $\{\varphi _{1},\varphi _{2},\varphi _{3},...,\varphi _{n}\}\models \psi$, тогда можно сформулировать как отсутствие контрпримера , где контрпример определяется как случай ${\mathcal {I}}$ в котором предпосылки аргумента $\{\varphi _{1},\varphi _{2},\varphi _{3},...,\varphi _{n}\}$ все верно, кроме заключения $\psi$ не правда. Как будет видно из § Семантическая истина, достоверность, следствие , это то же самое, что сказать, что заключение является семантическим следствием посылок.

Пропозициональная соединительная семантика

Основные статьи: Логическая связка и функция истины

Интерпретация напрямую присваивает семантические значения атомарным формулам . Молекулярным формулам присваивается функция стоимости составляющих их атомов в зависимости от используемой связки; связки определяются таким образом, что истинностное значение предложения, составленного из атомов со связками, зависит от истинностных значений атомов, к которым они применяются, и только от них. называет это предположение Колин Хаусон предположением об функциональности связок . истинности -

Поскольку логические связки определяются семантически только в терминах значений истинности , которые они принимают, когда пропозициональные переменные , к которым они применяются, принимают одно из двух возможных значений истинности, семантическое определение связок обычно представляется в виде таблицы истинности для каждой из связок, как показано ниже:

п	д	п ∧ q	п ∨ q	п → д	п ↔ q	¬p	¬q
Т	Т	Т	Т	Т	Т	Ф	Ф
Т	Ф	Ф	Т	Ф	Ф	Ф	Т
Ф	Т	Ф	Т	Т	Ф	Т	Ф
Ф	Ф	Ф	Ф	Т	Т	Т	Т

Эта таблица охватывает каждую из пяти основных логических связок : конъюнкция (здесь обозначена p ∧ q), дизъюнкция (p ∨ q), импликация (p → q), двуусловие (p ↔ q) и отрицание (¬p или ¬q, в зависимости от обстоятельств). Этого достаточно для определения семантики каждого из этих операторов. Подробнее о каждой из пяти читайте в статьях о каждой конкретной, а также в статьях « Логическая связка » и « Функция истинности ». Дополнительные таблицы истинности для большего количества различных видов связок см. в статье « Таблица истинности ».

Некоторые из этих связок можно определить через другие: например, импликация p → q может быть определена в терминах дизъюнкции и отрицания, как ¬p ∨ q; а дизъюнкция может быть определена в терминах отрицания и конъюнкции как ¬(¬p ∧ ¬q). Фактически это истинно-функционально полная система, в том смысле, что все и только классические пропозициональные тавтологии являются теоремами, могут быть получены с использованием только дизъюнкции и отрицания (как это сделали Рассел , Уайтхед и Гильберт ), или используя только импликацию и отрицание (как это делал Фреге ), или используя только союз и отрицание, или даже используя только одну связку для «не и» ( штрих Шеффера ), как это сделал Жан Никод . Связка совместного отрицания ( логическое ИЛИ ) сама по себе также достаточна для определения всех остальных связок. но никакие другие связки не обладают этим свойством.

Некоторые авторы, а именно Хаусон и Каннингем, отличать эквивалентность от двуусловия. (Что касается эквивалентности, Хаусон называет ее «функционально-истинной эквивалентностью», а Каннингем называет ее «логической эквивалентностью».) Эквивалентность обозначается ⇔ и является метаязыковым символом, в то время как бикондиционал обозначается ↔ и является логической связкой в объектный язык ${\mathcal {L}}$. В любом случае, эквивалентность или бикондиционал истинны тогда и только тогда, когда связанным с ними формулам присваивается одно и то же семантическое значение при каждой интерпретации. Другие авторы часто не делают этого различия и могут использовать слово «эквивалентность». и/или символ ⇔, для обозначения двуусловной связки их объектного языка.

Семантическая истина, достоверность, последствия

Данный $\varphi$ и $\psi$ как формулы (или предложения) языка ${\mathcal {L}}$, и ${\mathcal {I}}$ как интерпретация (или случай) из ${\mathcal {L}}$, то применяются следующие определения:

• Правда в деле: Предложение $\varphi$ из ${\mathcal {L}}$ верно в соответствии с интерпретацией ${\mathcal {I}}$ если ${\mathcal {I}}$ значение истинности T присваивает $\varphi$. Если $\varphi$ верно ​ под ${\mathcal {I}}$, затем ${\mathcal {I}}$ называется моделью ​ $\varphi$.
• Ложь в случае: $\varphi$ является ложным в соответствии с интерпретацией ${\mathcal {I}}$ если и только если, $\neg \varphi$ верно под ${\mathcal {I}}$. Это определение ложности в случае как «истина отрицания». Ложность в случае также может быть определена с помощью определения «дополнения»: $\varphi$ является ложным в соответствии с интерпретацией ${\mathcal {I}}$ если и только если, $\varphi$ это неправда под ${\mathcal {I}}$. В классической логике эти определения эквивалентны, а в неклассической — нет.
• Семантическое следствие: предложение $\psi$ из ${\mathcal {L}}$ является смысловым следствием ( $\varphi \models \psi$) предложения $\varphi$ если нет толкования, согласно которому $\varphi$ это правда и $\psi$ не правда.
• Допустимая формула (тавтология): Предложение. $\varphi$ из ${\mathcal {L}}$ верно логически ( $\models \varphi$), или тавтология , если это верно при любой интерпретации, или правда в каждом случае.
• Согласованное предложение: Предложение ${\mathcal {L}}$является непротиворечивым , если оно истинно хотя бы при одной интерпретации. Оно непоследовательно , если оно непоследовательно. Несогласованную формулу еще называют самопротиворечивой . и сказал, что это внутреннее противоречие , или просто противоречие , хотя это последнее имя иногда резервируется специально для операторов формы $(p\land \neg p)$.

Для толкований (кейсов) ${\mathcal {I}}$ из ${\mathcal {L}}$, иногда даются такие определения:

• Полное дело: Дело ${\mathcal {I}}$ является полным тогда и только тогда, когда либо $\varphi$ верно в- ${\mathcal {I}}$ или $\neg \varphi$ верно в- ${\mathcal {I}}$, для любого $\varphi$ в ${\mathcal {L}}$.
• Последовательный случай: Случай ${\mathcal {I}}$ является непротиворечивым тогда и только тогда, когда не существует $\varphi$ в ${\mathcal {L}}$ такой, что оба $\varphi$ и $\neg \varphi$ верны в- ${\mathcal {I}}$.

Для классической логики , которая предполагает, что все случаи полны и непротиворечивы, применимы следующие теоремы:

• Для любой данной интерпретации данная формула либо истинна, либо ложна.
• Ни одна формула не является одновременно истинной и ложной при одной и той же интерпретации.
• $\varphi$ верно под ${\mathcal {I}}$ если и только если, $\neg \varphi$ является ложным под ${\mathcal {I}}$; $\neg \varphi$ верно под ${\mathcal {I}}$ если и только если, $\varphi$ это неправда под ${\mathcal {I}}$.
• Если $\varphi$ и $(\varphi \to \psi )$ оба верны под ${\mathcal {I}}$, затем $\psi$ верно под ${\mathcal {I}}$.
• Если $\models \varphi$ и $\models (\varphi \to \psi )$, затем $\models \psi$.
• $(\varphi \to \psi )$ верно под ${\mathcal {I}}$ тогда и только тогда, когда либо $\varphi$ это неправда под ${\mathcal {I}}$, или $\psi$ верно под ${\mathcal {I}}$.
• $\varphi \models \psi$ если и только если, $(\varphi \to \psi )$ , логически обоснован то есть $\varphi \models \psi$ если и только если, $\models (\varphi \to \psi )$.

Системы доказательств

См. Также: Теория доказательств и Исчисление доказательств.

Системы доказательств в логике высказываний можно широко разделить на системы семантических доказательств и системы синтаксических доказательств . в зависимости от типа логического следствия , на которое они опираются: системы семантических доказательств полагаются на семантическое следствие ( $\varphi \models \psi$), тогда как системы синтаксического доказательства полагаются на синтаксическое следствие ( $\varphi \vdash \psi$). Семантическое следствие имеет дело с истинностными значениями предложений во всех возможных интерпретациях, тогда как синтаксическое следствие касается вывода выводов из посылок на основе правил и аксиом внутри формальной системы. В этом разделе дается очень краткий обзор видов систем доказательств с привязками к соответствующим разделам этой статьи по каждой из них, а также к отдельным статьям Википедии по каждой из них.

Системы семантического доказательства

Пример таблицы истинности

Графическое представление частично построенной пропозициональной таблицы.

Системы семантических доказательств опираются на концепцию семантических последствий, символизируемую как $\varphi \models \psi$, что указывает на то, что если $\varphi$ верно, тогда $\psi$ также должно быть истинным во всех возможных интерпретациях.

Таблицы истинности

Основная статья: Таблица истинности

Таблица истинности — это метод семантического доказательства, используемый для определения истинного значения выражения пропозициональной логики во всех возможных сценариях. Путем исчерпывающего перечисления истинностных значений составляющих ее атомов таблица истинности может показать, является ли предложение истинным, ложным, тавтологичным или противоречивым. См. § Семантическое доказательство с помощью таблиц истинности .

Семантические таблицы

Основная статья: Метод аналитических таблиц

Семантическая таблица — это еще один метод семантического доказательства, который систематически исследует истинность предложения. Он строит дерево, каждая ветвь которого представляет возможную интерпретацию задействованных предложений. Если каждое ответвление приводит к противоречию, исходное предложение считается противоречием, а его отрицание — тавтологией . См. § Семантическое доказательство с помощью таблиц .

Системы синтаксического доказательства

Правила исчисления секвенций высказываний LK в Генцена обозначениях

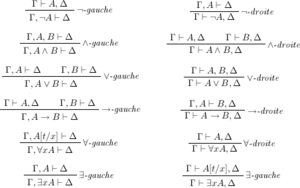
Системы синтаксического доказательства, напротив, фокусируются на формальном манипулировании символами в соответствии с конкретными правилами. Понятие синтаксического следствия, $\varphi \vdash \psi$, означает, что $\psi$ может быть получено из $\varphi$ используя правила формальной системы.

Аксиоматические системы

Основная статья: система Гильберта

Система аксиом – это набор аксиом или предположений, из которых логически выводятся другие утверждения (теоремы). В логике высказываний аксиоматические системы определяют базовый набор предложений, которые считаются самоочевидно истинными, а теоремы доказываются путем применения правил дедукции к этим аксиомам. См . § пример системы аксиоматических доказательств Яна Лукасевича .

Естественный вычет

Основная статья: Естественный вычет

Естественная дедукция — это синтаксический метод доказательства, который подчеркивает вывод выводов из посылок посредством использования интуитивных правил, отражающих обычное рассуждение. Каждое правило отражает ту или иную логическую связку и показывает, как ее можно ввести или исключить. См. § Синтаксическое доказательство посредством естественной дедукции .

Расчеты следуют

Основная статья: Секвенционное исчисление

Секвенциальное исчисление — это формальная система, которая представляет логические выводы в виде последовательностей или «секвенций» формул. Этот подход, разработанный Герхардом Генценом , фокусируется на структурных свойствах логических выводов и обеспечивает мощную основу для доказательства утверждений в рамках логики высказываний.

Семантическое доказательство с

См. также: Таблица истинности

Воспользовавшись семантической концепцией достоверности (истина в каждой интерпретации), можно доказать достоверность формулы с помощью таблицы истинности , которая дает все возможные интерпретации (присвоение значений истинности переменным) формулы. Если и только если все строки таблицы истинности оказываются истинными, формула семантически верна (истинна в любой интерпретации). Далее, если (и только если) $\neg \varphi$ действителен, то $\varphi$ является противоречивым.

Например, эта таблица показывает, что « p → (q ∨ r → (r → ¬p)) » недопустимо:

п	д	р	д ∨ р	р → ¬ п	q ∨ р → ( р → ¬ п )	п → ( q ∨ р → ( р → ¬ п ))
Т	Т	Т	Т	Ф	Ф	Ф
Т	Т	Ф	Т	Т	Т	Т
Т	Ф	Т	Т	Ф	Ф	Ф
Т	Ф	Ф	Ф	Т	Т	Т
Ф	Т	Т	Т	Т	Т	Т
Ф	Т	Ф	Т	Т	Т	Т
Ф	Ф	Т	Т	Т	Т	Т
Ф	Ф	Ф	Ф	Т	Т	Т

Вычисление последнего столбца третьей строки может быть отображено следующим образом:

п	→	(q	∨	р	→	(р	→	¬	п))
Т	→	(Ф	∨	Т	→	(Т	→	¬	Т))
Т	→	(	Т		→	(Т	→	Ф	))
Т	→	(	Т		→		Ф		)
Т	→				Ф
	Ф
Т	Ф	Ф	Т	Т	Ф	Т	Ф	Ф	Т

Далее, используя теорему о том, что $\varphi \models \psi$ если и только если, $(\varphi \to \psi )$ действует, мы можем использовать таблицу истинности, чтобы доказать, что формула является семантическим следствием набора формул: $\{\varphi _{1},\varphi _{2},\varphi _{3},...,\varphi _{n}\}\models \psi$ тогда и только тогда, когда мы можем создать таблицу истинности, которая окажется верной для формулы $\left(\left(\bigwedge _{i=1}^{n}\varphi _{i}\right)\rightarrow \psi \right)$ (то есть, если $\models \left(\left(\bigwedge _{i=1}^{n}\varphi _{i}\right)\rightarrow \psi \right)$).

Семантическое доказательство с помощью таблиц

Основная статья: Метод аналитических таблиц

Поскольку таблицы истинности имеют 2 ^н строки для n переменных, они могут быть утомительно длинными для больших значений n. Аналитические таблицы являются более эффективным, но, тем не менее, механическим методом. семантический метод доказательства; они пользуются тем фактом, что «мы ничего не узнаем о достоверности вывода, исследуя распределения истинностных значений, которые делают либо посылки ложными, либо заключение истинным: единственные релевантные распределения при рассмотрении дедуктивной валидности — это, очевидно, только те распределения, которые делают посылки истинны, а заключение ложно».

Аналитические таблицы для пропозициональной логики полностью определяются правилами, схематически изложенными ниже. В этих правилах используются «формулы со знаком», где формула со знаком является выражением. $TX$ или $FX$, где $X$ это (беззнаковая) формула языка ${\mathcal {L}}$. (Неофициально, $TX$ читается " $X$ это правда», и $FX$ читается " $X$ неверно».) Их формальное семантическое определение состоит в том, что «при любой интерпретации подписанная формула $TX$ называется истинным, если $X$ истинно и ложно, если $X$ неверно, тогда как знаковая формула $FX$ называется ложным, если $X$ верно, и верно, если $X$ ложно».

${\begin{aligned}&1)\quad {\frac {T\sim X}{FX}}\quad &&{\frac {F\sim X}{TX}}\\{\phantom {spacer}}\\&2)\quad {\frac {T(X\land Y)}{\begin{matrix}TX\\TY\end{matrix}}}\quad &&{\frac {F(X\land Y)}{FX|FY}}\\{\phantom {spacer}}\\&3)\quad {\frac {T(X\lor Y)}{TX|TY}}\quad &&{\frac {F(X\lor Y)}{\begin{matrix}FX\\FY\end{matrix}}}\\{\phantom {spacer}}\\&4)\quad {\frac {T(X\supset Y)}{FX|TY}}\quad &&{\frac {F(X\supset Y)}{\begin{matrix}TX\\FY\end{matrix}}}\end{aligned}}$

В этих обозначениях правило 2 означает, что $T(X\land Y)$ дает оба $TX,TY$, тогда как $F(X\land Y)$ разветвляется на $FX,FY$. Обозначения следует понимать аналогично правилам 3 и 4. Часто в таблицах классической логики обозначение формулы со знаком упрощается так, что $T\varphi$ пишется просто как $\varphi$, и $F\varphi$ как $\neg \varphi$, что объясняет название правила 1 « Правило двойного отрицания ».

Таблицу для набора формул составляют, применяя правила для создания большего количества строк и ветвей дерева до тех пор, пока не будет использована каждая строка, создавая полную таблицу. В некоторых случаях ветка может содержать оба $TX$ и $FX$ для некоторых $X$, то есть противоречие. В этом случае говорят, что ветка закрывается . Если каждая ветвь дерева закрывается, говорят, что закрывается само дерево. В соответствии с правилами построения таблиц замкнутое дерево является доказательством того, что исходная формула или набор формул, использованных для его построения, сама была противоречивой и, следовательно, ложной. И наоборот, таблица также может доказать, что логическая формула тавтологична : если формула тавтологична, ее отрицание является противоречием, поэтому таблица, построенная на основе ее отрицания, закроется.

Чтобы построить таблицу для аргумента $\langle \{\varphi _{1},\varphi _{2},\varphi _{3},...,\varphi _{n}\},\psi \rangle$, сначала выписывают набор формул посылок, $\{\varphi _{1},\varphi _{2},\varphi _{3},...,\varphi _{n}\}$, с одной формулой в каждой строке, подписанной знаком $T$ (то есть, $T\varphi$ для каждого $T\varphi$ в комплекте); и вместе с этими формулами (порядок неважен) выписывают и вывод: $\psi$, подписал с $F$ (то есть, $F\psi$). Затем создается дерево истинности (аналитическая таблица), используя все эти строки в соответствии с правилами. Замкнутое дерево будет доказательством того, что аргумент верен, поскольку $\varphi \models \psi$ если и только если, $\{\varphi ,\sim \psi \}$ противоречиво (также пишется как $\varphi ,\sim \psi \models$).

Список классически

Используя методы семантической проверки, такие как таблицы истинности или семантические таблицы, для проверки тавтологий и семантических последствий, можно показать, что в классической логике следующие классические формы аргументов семантически действительны, т. е. эти тавтологии и семантические последствия верны. Мы используем $\varphi$ ⟚ $\psi$ для обозначения эквивалентности $\varphi$ и $\psi$, то есть как сокращение для обоих $\varphi \models \psi$ и $\psi \models \varphi$; Для облегчения чтения символов дано описание каждой формулы. В описании символ ⊧ (называемый «двойной турникет») читается как «следовательно», что является его общепринятым прочтением. хотя многие авторы предпочитают читать это как «влечет за собой», или как «модели».

Имя	секвентальный	Описание
Режим настройки	$((p\to q)\land p)\models q$	Если р, то q ; п ; поэтому q
Удаление режима	$((p\to q)\land \neg q)\models \neg p$	Если р, то q ; не д ; поэтому не п
Гипотетический силлогизм	$((p\to q)\land (q\to r))\models (p\to r)$	Если р, то q ; если q , то r ; следовательно, если p , то r
Дизъюнктивный силлогизм	$((p\lor q)\land \neg p)\models q$	Либо p , либо q , либо оба; не п ; следовательно, q
Конструктивная дилемма	$((p\to q)\land (r\to s)\land (p\lor r))\models (q\lor s)$	Если р, то q ; и если г, то s ; но п или р ; поэтому q или s
Разрушительная дилемма	$((p\to q)\land (r\to s)\land (\neg q\lor \neg s))\models (\neg p\lor \neg r)$	Если р, то q ; и если г, то s ; но не q или не s ; поэтому ни п , ни не р
Двунаправленная дилемма	$((p\to q)\land (r\to s)\land (p\lor \neg s))\models (q\lor \neg r)$	Если р, то q ; и если г, то s ; но р или нет s ; поэтому q или нет r
Упрощение	$(p\land q)\models p$	p и q верны; следовательно, p истинно
Соединение	$p,q\models (p\land q)$	p и q верны по отдельности; следовательно, они истинны вместе
Добавление	$p\models (p\lor q)$	р верно; следовательно, дизъюнкция ( p или q ) верна
Состав	$((p\to q)\land (p\to r))\models (p\to (q\land r))$	Если р, то q ; и если р , то р ; следовательно, если p истинно, то q и r истинны
Теорема де Моргана (1)	$\neg (p\land q)$ ⟚ $(\neg p\lor \neg q)$	Отрицание ( p и q ) эквивалентно. to (не p или не q )
Теорема Моргана (2)	$\neg (p\lor q)$ ⟚ $(\neg p\land \neg q)$	Отрицание ( p или q ) эквивалентно. to (не p и не q )
Коммутация (1)	$(p\lor q)$ ⟚ $(q\lor p)$	( p или q ) эквивалентно. к ( q или p )
Коммутация (2)	$(p\land q)$ ⟚ $(q\land p)$	( p и q ) экв. к ( q и p )
Коммутация (3)	$(p\leftrightarrow q)$ ⟚ $(q\leftrightarrow p)$	( p тогда и только тогда, когда q ) экв. to ( q тогда и только тогда, когда p )
Ассоциация (1)	$(p\lor (q\lor r))$ ⟚ $((p\lor q)\lor r)$	p или ( q или r ) эквивалентно. to ( p или q ) или r
Ассоциация (2)	$(p\land (q\land r))$ ⟚ $((p\land q)\land r)$	p и ( q и r ) эквивалентны. к ( p и q ) и r
Распределение (1)	$(p\land (q\lor r))$ ⟚ $((p\land q)\lor (p\land r))$	p и ( q или r ) эквивалентны. к ( p и q ) или ( p и r )
Распределение (2)	$(p\lor (q\land r))$ ⟚ $((p\lor q)\land (p\lor r))$	p или ( q и r ) эквивалентны. к ( p или q ) и ( p или r )
Двойное отрицание	$p$ ⟚ $\neg \neg p$	p эквивалентно отрицанию not p
Транспонирование	$(p\to q)$ ⟚ $(\neg q\to \neg p)$	Если p, то q эквивалентно. если не q , то не p
Материальное значение	$(p\to q)$ ⟚ $(\neg p\lor q)$	Если p, то q эквивалентно. чтобы не p или q
Эквивалентность материалов (1)	$(p\leftrightarrow q)$ ⟚ $((p\to q)\land (q\to p))$	( p тогда и только тогда, когда q ) экв. (если p истинно, то q истинно) и (если q истинно, то p истинно)
Эквивалентность материалов (2)	$(p\leftrightarrow q)$ ⟚ $((p\land q)\lor (\neg p\land \neg q))$	( p тогда и только тогда, когда q ) экв. либо ( p и q истинны), либо (оба p и q ложны)
Эквивалентность материалов (3)	$(p\leftrightarrow q)$ ⟚ $((p\lor \neg q)\land (\neg p\lor q))$	( p тогда и только тогда, когда q ) эквивалентно ., как ( p или не q истинно), так и (не p или q истинно)
Экспорт	$((p\land q)\to r)\models (p\to (q\to r))$	из (если p и q истинны, то r истинно) мы можем доказать (если q истинно, то r истинно, если p истинно)
Импорт	$(p\to (q\to r))$ ⟚ $((p\land q)\to r)$	Если p , то (если q , то r ) эквивалентно тому, что если p и q , то r
Тавтология (1)	$p$ ⟚ $(p\lor p)$	p верно, эквивалентно. для p верно или p верно
Тавтология (2)	$p$ ⟚ $(p\land p)$	p верно, эквивалентно. для p верно и p верно
Третье не дано (Закон исключенного третьего)	$\models (p\lor \neg p)$	р или не р правда
Закон непротиворечия	$\models \neg (p\land \neg p)$	p , а не p — ложь, это истинное утверждение
Взрыв	$(p\land \neg p)\models q$	р и не р ; поэтому q

Синтаксическое доказательство посредством естественной дедукции

Основная статья: Естественный вычет

Естественный вывод , поскольку это метод синтаксического доказательства, определяется путем предоставления правил вывода (также называемых правилами доказательства ). для языка с типичным набором связок $\{-,\&,\lor ,\to ,\leftrightarrow \}$; никакие аксиомы, кроме этих правил, не используются. Правила описаны ниже, а затем приводится подтверждающий пример.

Стили обозначений

Разные авторы в некоторой степени различаются относительно того, какие правила вывода они предлагают, что будет отмечено. Однако более поразительным для внешнего вида доказательства являются различия в стилях обозначений. Обозначение § Генцена , которое было рассмотрено ранее для краткого рассуждения, на самом деле может быть сложено для получения больших древовидных доказательств естественного вывода. — не путать с «деревьями истинности», другим названием аналитических таблиц . Существует также стиль Станислава Ясковского , где формулы в доказательстве записываются внутри различных вложенных блоков. и существует упрощение стиля Ясковского благодаря Фредрику Фитчу ( обозначение Фитча ), где рамки упрощены до простых горизонтальных линий под введением предположений и вертикальных линий слева от строк, которые находятся под предположением. Наконец, есть единственный стиль обозначений, который фактически будет использоваться в этой статье, и принадлежит Патрику Суппесу . но был очень популяризирован Э. Дж. Леммоном и Бенсоном Мейтсом . Этот метод имеет то преимущество, что графически он наименее трудоемкий в создании и отображении, что сделало его естественным выбором для редактора, написавшего эту часть статьи, который не понимал сложных команд LaTeX , которые потребуются для создания доказательства другими методами.

, Таким образом , доказательство изложенное в соответствии со стилем обозначений Суппеса-Леммона , представляет собой последовательность строк, содержащих предложения, где каждое предложение является либо предположением, либо результатом применения правила доказательства к предыдущим предложениям в последовательности. Каждая строка доказательства состоит из предложения доказательства вместе с его аннотацией , набором предположений и текущим номером строки . В наборе предположений перечислены предположения, от которых зависит данное предложение доказательства, на которые ссылаются номера строк. Аннотация указывает, какое правило доказательства было применено и к каким предыдущим строкам было получено текущее предложение. См. § Пример доказательства естественного вывода .

Правила вывода

Правила естественного вывода, созданные, в конечном счете, Генценом , приведены ниже. Существует десять примитивных правил доказательства, которые представляют собой правило предположения , плюс четыре пары правил введения и исключения для бинарных связок, а также правило reductio ad adbsurdum . Дизъюнктивный силлогизм можно использовать как более простую альтернативу правильному ∨-исключению, а MTT и DN — это обычно заданные правила, хотя они не примитивны.

Список правил вывода

Имя правила	Альтернативные названия	Аннотация	Успенский набор	Заявление
Правило предположений	Предположение	А	Текущий номер строки.	На любой стадии аргументации вводите предложение как предположение аргумента.
Знакомство с союзом	Знакомство с амперсандом, союз (CONJ)	м, н и я	Объединение наборов допущений в строках m и n .	От $\varphi$ и $\psi$ в строках m и n сделайте вывод $\varphi ~\&~\psi$.
Устранение союза	Упрощение (S), устранение амперсанда	мне	То же, что и в строке m .	От $\varphi ~\&~\psi$ в строке m сделайте вывод $\varphi$ и $\psi$.
Введение в дизъюнкцию	Дополнение (ДОБАВИТЬ)	м ∨I	То же, что и в строке m .	От $\varphi$ в строке m сделайте вывод $\varphi \lor \psi$, что бы ни $\psi$ может быть.
Устранение дизъюнкции	Устранение клина, дилемма (DL)	j,k,l,m,n ∨E	Линии j,k,l,m,n .	От $\varphi \lor \psi$ в строке j и предположение о $\varphi$ в строке k и вывод $\chi$ от $\varphi$ в строке l и предположение о $\psi$ в строке m и вывод $\chi$ от $\psi$ в строке n сделайте вывод $\chi$.
Дизъюнктивный силлогизм	Устранение клина (∨E), метод удаления и размещения (MTP)	м,н ДС	Объединение наборов допущений в строках m и n .	От $\varphi \lor \psi$ на линии м и $-\varphi$ в строке n сделайте вывод $\psi$; от $\varphi \lor \psi$ на линии м и $-\psi$ в строке n сделайте вывод $\varphi$.
Устранение стрелы	настройка режима (МПП), настройка режима (МП), условное исключение	м, н →Е	Объединение наборов допущений в строках m и n .	От $\varphi \to \psi$ в строке m и $\varphi$ в строке n сделайте вывод $\psi$.
Знакомство со стрелкой	Условное доказательство (CP), условное введение	п, →I (м)	Все в предположении, заданном в строке n , за исключением m , строки, где предполагался антецедент.	От $\psi$ в строке n , что следует из предположения о $\varphi$ в строке m сделайте вывод $\varphi \to \psi$.
Доведение до абсурда	Косвенное доказательство (IP), введение отрицания (−I), устранение отрицания (-E)	м,   н   РАА   (к)	Объединение наборов предположений в строках m и n , исключая k (опровергнутое предположение).	Из приговора и его отрицания в строках m и n сделайте вывод об отрицании любого предположения, появляющегося в доказательстве (в строке k ).
Знакомство с двойной стрелкой	Двуусловное определение ( Df ↔), двуусловное введение	м, н ↔ я	Объединение наборов допущений в строках m и n .	От $\varphi \to \psi$ и $\psi \to \varphi$ в строках m и n сделайте вывод $\varphi \leftrightarrow \psi$.
Устранение двойной стрелки	Двуусловное определение ( Df ↔), двуусловное исключение	м ↔ Е	То же, что и в строке m .	От $\varphi \leftrightarrow \psi$ в строке m сделайте вывод либо $\varphi \to \psi$ или $\psi \to \varphi$.
Двойное отрицание	Устранение двойного отрицания	мДН	То же, что и в строке m .	От $--\varphi$ в строке m сделайте вывод $\varphi$.
Способ снятия удаления	Режим подъема (MT)	м, н МТТ	Объединение наборов допущений в строках m и n .	От $\varphi \to \psi$ в строке m и $-\psi$ в строке n сделайте вывод $-\varphi$.

вычета

Доказательство ниже выводит $-P$ от $P\to Q$ и $-Q$ используя только MPP и RAA , что показывает, что MTT не является примитивным правилом, поскольку его можно вывести из этих двух других правил.

Вывод MTT из MPP и RAA

Успенский набор	Номер строки	Доказательное предложение	Аннотация
1	1	$P\to Q$	А
2	2	$-Q$	А
3	3	$P$	А
1 , 3	4	$Q$	1 , 3 →E
1 , 2	5	$-P$	2 , 4 РАА

синтаксического доказательства

Основные статьи: Теория доказательств и исчисление доказательств

Рассмотрим еще раз логическую форму аргумента § Пример , формализованную, как в § Формализация :

${\begin{array}{rl}1.&P\to Q\\2.&P\\\hline \therefore &Q\end{array}}$

Логической формой этого аргумента является modus ponens , который является классически допустимой формой. Это обобщает схематически. Таким образом, где φ и ψ могут быть вообще любыми предложениями, а не только атомарными предложениями (ср. § Константы и схемы ):

${\begin{array}{rl}1.&\varphi \to \psi \\2.&\varphi \\\hline \therefore &\psi \end{array}}$

Другие формы аргументов удобны, но не обязательны. Учитывая полный набор аксиом (один из таких наборов см. ниже), modus ponens достаточен для доказательства всех других форм аргументов в логике высказываний, поэтому их можно рассматривать как производные. Обратите внимание: это не относится к расширению логики высказываний на другие логики, такие как логика первого порядка . Логика первого порядка требует по крайней мере одного дополнительного правила вывода для достижения полноты .

Значение аргумента в формальной логике состоит в том, что из установленных истин можно получить новые истины. В первом примере выше, учитывая две посылки, истинность Q еще не известна и не заявлена. После того, как аргумент приведен, Q. выводится Таким образом, мы определяем систему вывода как набор всех предложений, которые могут быть выведены из другого набора предложений. Например, учитывая набор предложений $A=\{P\lor Q,\neg Q\land R,(P\lor Q)\to R\}$, мы можем определить систему вывода Γ , которая представляет собой набор всех предложений, следующих из A . Повторение всегда предполагается, поэтому $P\lor Q,\neg Q\land R,(P\lor Q)\to R\in \Gamma$. Кроме того, из первого элемента A , последнего элемента, а также modus ponens R является следствием, и поэтому $R\in \Gamma$. Однако, поскольку мы не включили достаточно полные аксиомы, ничего другого вывести невозможно. Таким образом, хотя большинство систем дедукции, изучаемых в логике высказываний, способны выводить $(P\lor Q)\leftrightarrow (\neg P\to Q)$, этот слишком слаб, чтобы доказать такое утверждение.

Формальная структура, например, системы

Одним из основных применений исчисления высказываний при его интерпретации для логических приложений является определение отношений логической эквивалентности между формулами высказываний. Эти отношения определяются с помощью имеющихся правил преобразования, последовательности которых называются выводами или доказательствами .

Следующие примеры систем доказательства для исчисления высказываний предполагают, что исчисление определяется как формальная система. ${\mathcal {L}}={\mathcal {L}}\left(\mathrm {A} ,\ \Omega ,\ \mathrm {Z} ,\ \mathrm {I} \right)$, где:

• Альфа -набор $\mathrm {A}$ представляет собой счетное бесконечное множество ${\mathcal {L}}$атомарные формулы или пропозициональные переменные . В последующих примерах элементы $\mathrm {A}$ обычно это буквы p , q , r и так далее.
• Омега -множество Ω — это конечное множество элементов, называемых операторными символами или логическими связками . Множество Ω разбивается на непересекающиеся подмножества следующим образом: $\Omega =\Omega _{0}\cup \Omega _{1}\cup \cdots \cup \Omega _{j}\cup \cdots \cup \Omega _{m}.$, где, $\Omega _{j}$— набор операторных символов арности j . Например, разбиение Ω для типичных пяти связок будет иметь $\Omega _{1}=\{\lnot \},$ и $\Omega _{2}\subseteq \{\land ,\lor ,\to ,\leftrightarrow \}.$ Кроме того, постоянные логические значения рассматриваются как операторы нулевой арности, так что $\Omega _{0}=\{\bot ,\top \}.$

• Зета -сет $\mathrm {Z}$ — это конечный набор правил преобразования , называемых правилами вывода , когда они приобретают логические приложения.
• Набор йоты $\mathrm {I}$ представляет собой счетное множество начальных точек , которые называются аксиомами , когда получают логические интерпретации.

Язык ​ ${\mathcal {L}}$ представляет собой набор правильно построенных формул , индуктивно определяемых следующими правилами:

1. База: любой элемент альфа-набора. $\mathrm {A}$ представляет собой формулу ${\mathcal {L}}$.
2. Если $p_{1},p_{2},\ldots ,p_{j}$ представляют собой формулы и $f$ в $\Omega _{j}$, затем $fp_{1}p_{2}\ldots p_{j}$ это формула.
3. Закрыто: Ничто иное не является формулой ${\mathcal {L}}$.

Повторное применение этих правил позволяет строить сложные формулы. Примеры формул, которые следуют этим правилам, включают « p » (по правилу 1), « $\neg p$" (по правилу 2), " q " (по правилу 1) и " $\neg p\lor q$(по правилу 2).

В последующем обсуждении после определения системы доказательства доказательство представляется в виде последовательности пронумерованных строк, каждая из которых состоит из одной формулы, за которой следует причина или обоснование введения этой формулы. Каждая посылка аргумента, то есть предположение, введенное как гипотеза аргумента, указывается в начале последовательности и помечается как «посылка» вместо другого обоснования. Заключение указывается в последней строке. Доказательство считается полным, если каждая строка следует из предыдущих в результате правильного применения правила преобразования. (Для контрастного подхода см. деревья доказательств ).

системы аксиоматических доказательств

Позволять ${\mathcal {L}}_{Ax}={\mathcal {L}}(\mathrm {A} ,\Omega ,\mathrm {Z} ,\mathrm {I} )$, где $\mathrm {A}$, $\Omega$, $\mathrm {Z}$, $\mathrm {I}$ определяются следующим образом:

• Набор $\mathrm {A}$, счетный бесконечный набор символов, которые служат для представления логических предложений: $\mathrm {A} =\{p,q,r,s,t,u,p_{2},\ldots \}.$
• Функционально полная комплектация $\Omega$логических операторов (логических связок и отрицания) заключается в следующем. Из трех связок для соединения, дизъюнкции и импликации ( $\wedge ,\lor$, и → ), один можно считать примитивным, а два других можно определить через него и отрицание ( ¬ ). Альтернативно, все логические операторы могут быть определены в терминах единственного достаточного оператора , такого как штрих Шеффера (nand). Двуусловие ( $a\leftrightarrow b$), конечно, можно определить в терминах конъюнкции и импликации как $(a\to b)\land (b\to a)$. Принятие отрицания и импликации в качестве двух примитивных операций исчисления высказываний равносильно наличию набора омега. $\Omega =\Omega _{1}\cup \Omega _{2}$ разделен как $\Omega _{1}=\{\lnot \},$ и $\Omega _{2}=\{\to \}.$ Затем $a\lor b$ определяется как $\neg a\to b$, и $a\land b$ определяется как $\neg (a\to \neg b)$.

• Набор $\mathrm {I}$(множество начальных точек логического вывода, т. е. логических аксиом) — система аксиом, предложенная Яном Лукасевичем и используемая как часть исчисления высказываний системы Гильберта . Все аксиомы являются примерами замены :
  • $p\to (q\to p)$
  • $(p\to (q\to r))\to ((p\to q)\to (p\to r))$
  • $(\neg p\to \neg q)\to (q\to p)$
• Набор $\mathrm {Z}$ правил преобразования (правил вывода) является единственным правилом modus ponens (т. е. из любых формул вида $\varphi$ и $(\varphi \to \psi )$, сделать вывод $\psi$).

Эта система используется в Metamath set.mm. базе данных формальных доказательств

доказательства в системе аксиоматического

Теперь мы докажем ту же теорему $A\to A$ в аксиоматической системе Яна Лукасевича, описанной выше, которая является примером дедуктивной системы в стиле Гильберта для классического исчисления высказываний.

Аксиомы:

(А1) $(p\to (q\to p))$

(А2) $((p\to (q\to r))\to ((p\to q)\to (p\to r)))$

(А3) $((\neg p\to \neg q)\to (q\to p))$

И доказательство следующее:

1. $A\to ((B\to A)\to A)$ (пример (A1))
2. $(A\to ((B\to A)\to A))\to ((A\to (B\to A))\to (A\to A))$ (пример (A2))
3. $(A\to (B\to A))\to (A\to A)$ (из (1) и (2) путем настройки режима )
4. $A\to (B\to A)$ (пример (A1))
5. $A\to A$ (из (4) и (3) методом настройки)

Обоснованность и полнота правил

Важнейшими свойствами этого набора правил является то, что они надежны и полны . Неформально это означает, что правила верны и никаких других правил не требуется. Эти утверждения можно сделать более формальными следующим образом. Доказательства правильности и полноты логики высказываний сами по себе не являются доказательствами в логике высказываний; это теоремы в ZFC , используемые в качестве метатеории для доказательства свойств логики высказываний.

Мы определяем истинностное присвоение как функцию , которая отображает пропозициональные переменные в истинное или ложное . Неформально такое присвоение истинности можно понимать как описание возможного положения дел (или возможного мира ), в котором одни утверждения истинны, а другие — нет. Семантику формул затем можно формализовать, определив, для какого «положения дел» они считаются истинными, что и делается с помощью следующего определения.

Мы определяем, когда такое истинностное присвоение A удовлетворяет некоторой корректной формуле со следующими правилами:

• A удовлетворяет пропозициональной переменной P тогда и только тогда, когда A ( P ) = true
• A удовлетворяет ¬ φ тогда и только тогда, когда A не удовлетворяет φ
• A удовлетворяет ( φ ∧ ψ ) тогда и только тогда, когда A удовлетворяет как φ, так и ψ.
• A удовлетворяет ( φ ∨ ψ ) тогда и только тогда, когда A удовлетворяет хотя бы одному из φ или ψ
• A удовлетворяет ( φ → ψ ) тогда и только тогда, когда это не тот случай, когда A удовлетворяет φ , но не удовлетворяет ψ
• A удовлетворяет ( φ ↔ ψ ) тогда и только тогда, когда A удовлетворяет обоим φ и ψ или не удовлетворяет ни одному из них.

С помощью этого определения мы теперь можем формализовать, что означает, что формула φ следует из определенного набора S формул. Неформально это верно, если во всех возможных мирах с учетом набора формул S формула φ также выполняется . Это приводит к следующему формальному определению: мы говорим, что набор S корректных формул семантически влечет за собой (или подразумевает ) некоторую корректную формулу φ, если все назначения истинности, которые удовлетворяют всем формулам в S, также удовлетворяют φ .

Наконец, мы определяем синтаксическое следствие так, что φ синтаксически влечет за собой S тогда и только тогда, когда мы можем получить его с помощью правил вывода, которые были представлены выше, за конечное число шагов. Это позволяет нам точно сформулировать, что означает, что набор правил вывода является надежным и полным:

Правильность: если набор правильно составленных формул S синтаксически влечет за собой правильно составленную формулу φ, то S семантически влечет за собой φ .

Полнота: если набор правильно сформированных формул S семантически влечет за собой правильно сформированную формулу φ, то S синтаксически влечет за собой φ .

Для приведенного выше набора правил это действительно так.

Эскиз доказательства надежности

(Для большинства логических систем это сравнительно «простое» направление доказательства)

Соглашения об обозначениях: пусть G — переменная, охватывающая наборы предложений. Пусть A, B и C варьируются по предложениям. Поскольку « G синтаксически влечет за собой А », мы пишем « G доказывает А ». Поскольку « G семантически влечет за собой А », мы пишем « G подразумевает А ».

Мы хотим показать: ( A )( G ) (если G доказывает A , то G подразумевает A ).

Заметим, что « G доказывает А » имеет индуктивное определение, и это дает нам непосредственные ресурсы для демонстрации утверждений вида «Если G доказывает А , то...». Итак, наше доказательство проводится по индукции.

1. Основа. : Если A является членом G , то G подразумевает A. Докажите
2. Основа. Докажите: Если А — аксиома, то G следует А. из
3. Индуктивный шаг (индукция по n , длине доказательства):
   1. Предположим для произвольных G и A что если G доказывает A за n или меньше шагов, то G подразумевает A. ,
   2. Для каждого возможного применения правила вывода на шаге n +1 , приводящего к новой теореме B , покажите, что G следует B. из

Обратите внимание, что базисный шаг II можно опустить для систем естественной дедукции, поскольку они не имеют аксиом. При использовании Шага II необходимо показать, что каждая из аксиом является (семантической) логической истиной .

Шаги «Базис» демонстрируют, что простейшие доказуемые предложения из G также подразумеваются из G для G. любого (Доказательство простое, поскольку семантический факт, что множество подразумевает любой из своих членов, также тривиален.) На индуктивном этапе будут систематически охватываться все дальнейшие предложения, которые могут быть доказуемы, — путем рассмотрения каждого случая, в котором мы можем прийти к логическому выводу. используя правило вывода, и показывает, что если новое предложение доказуемо, оно также логически подразумевается. (Например, у нас может быть правило, говорящее нам, что из « А » мы можем вывести « А » или «В ». В III.a мы предполагаем, что если А доказуемо, то оно подразумевается. Мы также знаем, что если А доказуемо, то « A или B » доказуемо. Мы должны показать, что тогда также подразумевается « A или B ». Мы делаем это, апеллируя к семантическому определению и предположению, которое мы только что сделали. Мы предполагаем, что A доказуемо из G. Итак, это так. также подразумевается G. Таким образом, любая семантическая оценка, делающая все G истинным, делает A истинным, но любая оценка, делающая A истинным, делает « A» или «B » истинными в соответствии с определенной семантикой для «или». G true делает « A или B » истинным. Таким образом, подразумевается « А или Б ».) Как правило, индуктивный этап состоит из длительного, но простого каждом конкретном случае анализа всех правил вывода в , показывающего, что каждое из них «сохраняет» семантическую импликацию.

По определению доказуемости, не существует никаких предложений, которые можно было бы доказать, кроме как будучи членом G , аксиомой или следуя правилу; поэтому, если все это семантически подразумевается, дедуктивный расчет верен.

Эскиз доказательства полноты

(Обычно это гораздо более сложное направление доказательства.)

Мы принимаем те же обозначения, что и выше.

Мы хотим показать: если подразумевает A , то G доказывает A. G Мы действуем путем противопоставления : вместо этого мы показываем, что G не , доказывает A то G не из следует A. если Если мы покажем, что существует модель , в которой A не выполняется, несмотря на G истинность из G не следует A. , то, очевидно , Идея состоит в том, чтобы построить такую ​​модель на основе нашего предположения, что не доказывает A. G

1. G не A. доказывает (Предположение)
2. Если G не доказывает A , то мы можем построить (бесконечное) максимальное множество , G ^∗ , которое является надмножеством G и которое также не доказывает A .
   1. Упорядочите (с типом порядка ω) все предложения на языке (например, сначала самые короткие и одинаково длинные в расширенном алфавитном порядке) и пронумеруйте их ( E ₁ , E ₂ , ...)
   2. Определим серию G _n множеств ( G ₀ , G ₁ , ...) индуктивно:
      1. $G_{0}=G$
      2. Если $G_{k}\cup \{E_{k+1}\}$ доказывает A , тогда $G_{k+1}=G_{k}$
      3. Если $G_{k}\cup \{E_{k+1}\}$ не доказывает A то , $G_{k+1}=G_{k}\cup \{E_{k+1}\}$
   3. Определить G ^∗ как объединение всех G _n . (то есть Г. ^∗ — множество всех предложений, входящих в любой . _Gn )
   4. Можно легко показать, что
      1. г ^∗ содержит (является надмножеством) G (по (bi));
      2. г ^∗ не доказывает A (поскольку доказательство будет содержать только конечное число предложений, и когда последнее из них будет введено в некотором G _n , G _n докажет A вопреки определению G _n ); и
      3. г ^∗ является максимальным набором относительно A было добавлено еще какое-либо предложение : если к G ^∗ докажет А. , это если бы можно было добавить еще предложения, их следовало бы добавлять тогда, когда они встречались при построении Gn , _{(Потому что ,} опять же по определению)
3. Если Г ^∗ является максимальным множеством относительно A , то оно истинноподобно . Это означает, что он содержит C тогда и только тогда, когда он не содержит ¬C ; Если он содержит C и содержит «Если C , то B », то он также содержит B ; и так далее. Чтобы показать это, нужно показать, что аксиоматическая система достаточно сильна для следующего:
   • Для любых формул C и D , если доказываются и C и ¬C , то доказывается D. , Отсюда следует, что максимальное множество относительно A не может доказать одновременно C и ¬C доказывало бы A. , так как в противном случае оно
   • Для любых формул C и D если доказано C → D и ¬C → D , то доказано D. , Это используется вместе с теоремой о дедукции , чтобы показать, что для любой формулы либо она, либо ее отрицание находится в G ^∗ : Пусть B — формула, не принадлежащая G ^∗ ; тогда Г ^∗ добавлением B доказывает A. с Таким образом, из теоремы дедукции следует, что G ^∗ доказывает B → A. ​ Но предположим, что ¬B также не было в G ^∗ , то по той же логике G ^∗ также доказывает ¬B → A ; но тогда Г ^∗ доказывает A , ложность которого мы уже показали.
   • Для любых формул C и D , если доказано C и D то доказано C → D. ,
   • Для любых формул C и D , если доказано C и ¬D , то доказывается ¬( C → D ).
   • Для любых формул C и D , если доказывается ¬C то доказывается C → D. ,
   Если дополнительные логические операции (такие как конъюнкция и/или дизъюнкция) также являются частью словаря, то к аксиоматической системе предъявляются дополнительные требования (например, если она доказывает C и D , она также доказывает и их конъюнкцию).
4. Если Г ^∗ похоже на правду, есть G ^∗ -Каноническая оценка языка: такая, которая превращает каждое предложение в G ^∗ правда и все за пределами G ^∗ ложно, но при этом подчиняется законам семантической композиции в языке. Требование истинности необходимо для того, чтобы гарантировать, что это присвоение истинности будет удовлетворять законам семантической композиции в языке.
5. А Г ^∗ -каноническая оценка сделает наш исходный набор G истинным, а A — ложным.
6. Если существует оценка, при которой истинны , а A ложны, то G не (семантически) подразумевает A. G

Таким образом, каждая система, которая имеет modus ponens в качестве правила вывода и доказывает следующие теоремы (включая их замены), является полной:

• $p\to (\neg p\to q)$
• $(p\to q)\to ((\neg p\to q)\to q)$
• $p\to (q\to (p\to q))$
• $p\to (\neg q\to \neg (p\to q))$
• $\neg p\to (p\to q)$
• $p\to p$
• $p\to (q\to p)$
• $(p\to (q\to r))\to ((p\to q)\to (p\to r))$

Первые пять используются для удовлетворения пяти условий этапа III выше, а последние три — для доказательства теоремы дедукции.

Пример

В качестве примера можно показать, что, как и любая другая тавтология, три аксиомы классической системы исчисления высказываний, описанной ранее, могут быть доказаны в любой системе, которая удовлетворяет вышеизложенному, а именно, которая имеет modus ponens в качестве правила вывода и доказывает вышеизложенное. восемь теорем (включая их замены). Из восьми теорем последние две являются двумя из трех аксиом; третья аксиома, $(\neg q\to \neg p)\to (p\to q)$, также может быть доказано, как мы сейчас покажем.

Для доказательства мы можем использовать гипотетическую теорему о силлогизме (в форме, актуальной для этой аксиоматической системы), поскольку она опирается только на две аксиомы, которые уже входят в приведенный выше набор из восьми теорем. Доказательство тогда следующее:

1. $q\to (p\to q)$ (пример 7-й теоремы)
2. $(q\to (p\to q))\to ((\neg q\to \neg p)\to (q\to (p\to q)))$ (пример 7-й теоремы)
3. $(\neg q\to \neg p)\to (q\to (p\to q))$ (из (1) и (2) методом настройки)
4. $(\neg p\to (p\to q))\to ((\neg q\to \neg p)\to (\neg q\to (p\to q)))$ (пример теоремы о гипотетическом силлогизме)
5. $(\neg p\to (p\to q))$ (пример 5-й теоремы)
6. $(\neg q\to \neg p)\to (\neg q\to (p\to q))$ (из (5) и (4) методом настройки)
7. $(q\to (p\to q))\to ((\neg q\to (p\to q))\to (p\to q))$ (пример 2-й теоремы)
8. $((q\to (p\to q))\to ((\neg q\to (p\to q))\to (p\to q)))\to ((\neg q\to \neg p)\to ((q\to (p\to q))\to ((\neg q\to (p\to q))\to (p\to q))))$ (пример 7-й теоремы)
9. $(\neg q\to \neg p)\to ((q\to (p\to q))\to ((\neg q\to (p\to q))\to (p\to q)))$ (из (7) и (8) методом настройки)
10. $((\neg q\to \neg p)\to ((q\to (p\to q))\to ((\neg q\to (p\to q))\to (p\to q))))\to$

    $(((\neg q\to \neg p)\to (q\to (p\to q)))\to ((\neg q\to \neg p)\to ((\neg q\to (p\to q))\to (p\to q))))$ (пример 8-й теоремы)

11. $((\neg q\to \neg p)\to (q\to (p\to q)))\to ((\neg q\to \neg p)\to ((\neg q\to (p\to q))\to (p\to q)))$ (из (9) и (10) методом настройки)
12. $(\neg q\to \neg p)\to ((\neg q\to (p\to q))\to (p\to q))$ (из (3) и (11) методом настройки)
13. $((\neg q\to \neg p)\to ((\neg q\to (p\to q))\to (p\to q)))\to (((\neg q\to \neg p)\to (\neg q\to (p\to q)))\to ((\neg q\to \neg p)\to (p\to q)))$ (пример 8-й теоремы)
14. $((\neg q\to \neg p)\to (\neg q\to (p\to q)))\to ((\neg q\to \neg p)\to (p\to q))$ (из (12) и (13) в режиме настройки)
15. $(\neg q\to \neg p)\to (p\to q)$ (из (6) и (14) в режиме настройки)

полноты классической системы

Теперь мы проверим, что классическая система исчисления высказываний, описанная ранее, действительно может доказать необходимые восемь упомянутых выше теорем. Мы используем несколько доказанных здесь лемм :

(ДН1) $\neg \neg p\to p$ - Двойное отрицание (в одном направлении)

(ДН2) $p\to \neg \neg p$ - Двойное отрицание (другое направление)

(HS1) $(q\to r)\to ((p\to q)\to (p\to r))$ - одна из форм гипотетического силлогизма

(HS2) $(p\to q)\to ((q\to r)\to (p\to r))$ - другая форма гипотетического силлогизма.

(ТР1) $(p\to q)\to (\neg q\to \neg p)$ - Транспонирование

(ТР2) $(\neg p\to q)\to (\neg q\to p)$ - другая форма транспозиции.

(Л1) $p\to ((p\to q)\to q)$

(Л3) $(\neg p\to p)\to p$

Мы также используем метод метатеоремы гипотетического силлогизма как сокращение для нескольких шагов доказательства.

• $p\to (\neg p\to q)$ - доказательство:
  1. $p\to (\neg q\to p)$ (пример (A1))
  2. $(\neg q\to p)\to (\neg p\to \neg \neg q)$ (экземпляр (TR1))
  3. $p\to (\neg p\to \neg \neg q)$ (из (1) и (2) с использованием метатеоремы гипотетического силлогизма)
  4. $\neg \neg q\to q$ (экземпляр (DN1))
  5. $(\neg \neg q\to q)\to ((\neg p\to \neg \neg q)\to (\neg p\to q))$ (пример (HS1))
  6. $(\neg p\to \neg \neg q)\to (\neg p\to q)$ (из (4) и (5) с использованием modus ponens)
  7. $p\to (\neg p\to q)$ (из (3) и (6) с использованием метатеоремы гипотетического силлогизма)
• $(p\to q)\to ((\neg p\to q)\to q)$ - доказательство:
  1. $(p\to q)\to ((\neg q\to p)\to (\neg q\to q))$ (пример (HS1))
  2. $(\neg q\to q)\to q$ (пример (L3))
  3. $((\neg q\to q)\to q)\to (((\neg q\to p)\to (\neg q\to q))\to ((\neg q\to p)\to q))$ (пример (HS1))
  4. $((\neg q\to p)\to (\neg q\to q))\to ((\neg q\to p)\to q)$ (из (2) и (3) методом настройки)
  5. $(p\to q)\to ((\neg q\to p)\to q)$ (из (1) и (4) с использованием метатеоремы гипотетического силлогизма)
  6. $(\neg p\to q)\to (\neg q\to p)$ (пример (TR2))
  7. $((\neg p\to q)\to (\neg q\to p))\to (((\neg q\to p)\to q)\to ((\neg p\to q)\to q))$ (пример (HS2))
  8. $((\neg q\to p)\to q)\to ((\neg p\to q)\to q)$ (из (6) и (7) с использованием modus ponens)
  9. $(p\to q)\to ((\neg p\to q)\to q)$ (из (5) и (8) с использованием метатеоремы гипотетического силлогизма)
• $p\to (q\to (p\to q))$ - доказательство:
  1. $q\to (p\to q)$ (пример (A1))
  2. $(q\to (p\to q))\to (p\to (q\to (p\to q)))$ (пример (A1))
  3. $p\to (q\to (p\to q))$ (из (1) и (2) с использованием modus ponens)
• $p\to (\neg q\to \neg (p\to q))$ - доказательство:
  1. $p\to ((p\to q)\to q)$ (пример (L1))
  2. $((p\to q)\to q)\to (\neg q\to \neg (p\to q))$ (экземпляр (TR1))
  3. $p\to (\neg q\to \neg (p\to q))$ (из (1) и (2) с использованием метатеоремы гипотетического силлогизма)
• $\neg p\to (p\to q)$ - доказательство:
  1. $\neg p\to (\neg q\to \neg p)$ (пример (A1))
  2. $(\neg q\to \neg p)\to (p\to q)$ (пример (A3))
  3. $\neg p\to (p\to q)$ (из (1) и (2) с использованием метатеоремы гипотетического силлогизма)
• $p\to p$ - доказательство, приведенное в примере доказательства выше
• $p\to (q\to p)$ - аксиома (А1)
• $(p\to (q\to r))\to ((p\to q)\to (p\to r))$ - аксиома (А2)

Еще один план доказательства полноты

Если формула является тавтологией , то для нее существует таблица истинности , которая показывает, что каждая оценка дает истинное значение для формулы. Рассмотрим такую ​​оценку. С помощью математической индукции по длине подформул покажите, что истинность или ложность подформулы следует из истинности или ложности (в зависимости от оценки) каждой пропозициональной переменной в подформуле. Затем объедините строки таблицы истинности вместе по две, используя «( P истинно, подразумевает S ) подразумевает (( P ложно, подразумевает S ) подразумевает S )». Продолжайте повторять это до тех пор, пока не будут устранены все зависимости от пропозициональных переменных. В результате мы доказали данную тавтологию. Поскольку любая тавтология доказуема, логика полна.

аксиоматического доказательства

Можно определить другую версию исчисления высказываний, которая определяет большую часть синтаксиса логических операторов посредством аксиом и использует только одно правило вывода.

Аксиомы

Пусть φ , χ и ψ обозначают корректные формулы. (Сами правильно составленные формулы не будут содержать греческих букв, а будут содержать только заглавные латинские буквы, соединительные операторы и круглые скобки.) Тогда аксиомы будут следующими:

Аксиомы

Имя	Схема аксиом	Описание
ТОГДА-1	$\phi \to (\chi \to \phi )$	Добавить гипотезу χ , введение импликации
ТОГДА-2	$(\phi \to (\chi \to \psi ))\to ((\phi \to \chi )\to (\phi \to \psi ))$	Распределить гипотезу $\phi$ чрезмерная импликация
И-1	$\phi \land \chi \to \phi$	Устранить союз
И-2	$\phi \land \chi \to \chi$
И-3	$\phi \to (\chi \to (\phi \land \chi ))$	Ввести союз
ОР-1	$\phi \to \phi \lor \chi$	Ввести дизъюнкцию
ОР-2	$\chi \to \phi \lor \chi$
ОР-3	$(\phi \to \psi )\to ((\chi \to \psi )\to (\phi \lor \chi \to \psi ))$	Устранить дизъюнкцию
НЕ-1	$(\phi \to \chi )\to ((\phi \to \neg \chi )\to \neg \phi )$	Ввести отрицание
НЕ-2	$\phi \to (\neg \phi \to \chi )$	Устранить отрицание
НЕ-3	$\phi \lor \neg \phi$	Исключена середина, классическая логика
МКФ-1	$(\phi \leftrightarrow \chi )\to (\phi \to \chi )$	Устранить эквивалентность
МКФ-2	$(\phi \leftrightarrow \chi )\to (\chi \to \phi )$
МКФ-3	$(\phi \to \chi )\to ((\chi \to \phi )\to (\phi \leftrightarrow \chi ))$	Ввести эквивалентность

• Аксиому THEN-2 можно рассматривать как «распределительное свойство импликации относительно импликации».
• Аксиомы И-1 и И-2 соответствуют «устранению соединения». Отношение между AND-1 и AND-2 отражает коммутативность оператора конъюнкции.
• Аксиома AND-3 соответствует «введению союза».
• Аксиомы ОР-1 и ОР-2 соответствуют «введению дизъюнкции». Связь между OR-1 и OR-2 отражает коммутативность оператора дизъюнкции.
• Аксиома НЕ-1 соответствует «доведению до абсурда».
• Аксиома НЕ-2 гласит, что «из противоречия можно вывести все».
• Аксиома НЕ-3 называется « tertium non-datur » ( лат . «третье не дано») и отражает семантическую оценку пропозициональных формул: формула может иметь истинностное значение либо истинное, либо ложное. Третьего истинностного значения не существует, по крайней мере, в классической логике. Логики-интуиционисты не принимают аксиому НЕ-3 .

Правило вывода

Правило вывода – это способ выразить :

${\frac {\phi ,\ \phi \to \chi }{\chi }}$.

Правило мета-вывода

Пусть демонстрация представлена ​​последовательностью, в которой гипотезы располагаются слева от турникета , а выводы — справа от турникета. Тогда теорему о дедукции можно сформулировать следующим образом:

Если последовательность

$\phi _{1},\ \phi _{2},\ ...,\ \phi _{n},\ \chi \vdash \psi$

было продемонстрировано, то можно также продемонстрировать последовательность

$\phi _{1},\ \phi _{2},\ ...,\ \phi _{n}\vdash \chi \to \psi$.

Эта теорема о дедукции (DT) сама по себе не сформулирована с помощью исчисления высказываний: это не теорема исчисления высказываний, а теорема об исчислении высказываний. В этом смысле это метатеорема , сравнимая с теоремами о правильности или полноте исчисления высказываний.

С другой стороны, DT настолько полезен для упрощения процесса синтаксического доказательства, что его можно рассматривать и использовать как еще одно правило вывода, сопровождающее modus ponens. В этом смысле DT соответствует естественному правилу вывода условного доказательства , которое является частью первой версии исчисления высказываний, представленной в этой статье.

Обратное DT также справедливо:

Если последовательность

$\phi _{1},\ \phi _{2},\ ...,\ \phi _{n}\vdash \chi \to \psi$

было продемонстрировано, то можно также продемонстрировать последовательность

$\phi _{1},\ \phi _{2},\ ...,\ \phi _{n},\ \chi \vdash \psi$

на самом деле, справедливость обратного DT почти тривиальна по сравнению с DT:

Если

$\phi _{1},\ ...,\ \phi _{n}\vdash \chi \to \psi$

затем

1: $\phi _{1},\ ...,\ \phi _{n},\ \chi \vdash \chi \to \psi$

2: $\phi _{1},\ ...,\ \phi _{n},\ \chi \vdash \chi$

и из (1) и (2) можно вывести

3: $\phi _{1},\ ...,\ \phi _{n},\ \chi \vdash \psi$

посредством модус-полагания, QED

Обратное DT имеет важные последствия: его можно использовать для преобразования аксиомы в правило вывода. Например, по аксиоме И-1 имеем:

$\vdash \phi \wedge \chi \to \phi ,$

которое можно преобразовать с помощью обращения теоремы дедукции в

$\phi \wedge \chi \vdash \phi ,$

что говорит нам о том, что правило вывода

${\frac {\phi \wedge \chi }{\phi }}$

допустимо ​ . Это правило вывода — исключение конъюнкции , одно из десяти правил вывода, использованных в первой версии (в этой статье) исчисления высказываний.

Пример доказательства в более сложной аксиоматической системе

Ниже приведен пример (синтаксической) демонстрации, включающий только аксиомы THEN-1 и THEN-2 :

Доказывать: $A\to A$ (Рефлексивность импликации).

Доказательство:

1. $(A\to ((B\to A)\to A))\to ((A\to (B\to A))\to (A\to A))$

   Аксиома ТОГДА -2 с $\phi =A,\chi =B\to A,\psi =A$

2. $A\to ((B\to A)\to A)$

   Аксиома ТОГДА -1 с $\phi =A,\chi =B\to A$

3. $(A\to (B\to A))\to (A\to A)$

   Из (1) и (2), полагая

4. $A\to (B\to A)$

   Аксиома ТОГДА -1 с $\phi =A,\chi =B$

5. $A\to A$

   Из (3) и (4), полагая

Решатели

Одно заметное различие между исчислением высказываний и исчислением предикатов состоит в том, что выполнимость формулы высказываний разрешима . Определение выполнимости формул пропозициональной логики является NP-полной задачей. Однако существуют практические методы (например, алгоритм DPLL , 1962; алгоритм Чаффа , 2001), которые очень быстры для многих полезных случаев. Недавняя работа расширила алгоритмы решателя SAT для работы с предложениями, содержащими арифметические выражения ; это решатели SMT .

См. также

Высшие логические уровни

• Логика первого порядка
• Пропозициональная логика второго порядка
• Логика второго порядка
• Логика высшего порядка

Связанные темы

• Булева алгебра (логика)
• Булева алгебра (структура)
• Темы булевой алгебры
• Логический домен
• Булева функция
• Логическая функция
• Категорическая логика
• Комбинационная логика
• Комбинаторная логика
• Концептуальный график
• Дизъюнктивный силлогизм
• Существенный граф
• Эквациональная логика
• Экзистенциальный граф
• Исчисление высказываний Фреге
• Импликативное исчисление высказываний
• Интуиционистское исчисление высказываний
• Жан Буридан
• Законы формы
• Список логических символов
• Логический график
• Логическое НО
• Логическое значение
• Математическая логика
• Операция (математика)
• Павел Венецианский
• Закон Пирса
• Петр Испанский (автор)
• Пропозициональная формула
• Симметричная разница
• Тавтология (правило вывода)
• Функция истины
• Таблица истинности
• Уолтер Берли
• Уильям Шервудский

Further reading

• Brown, Frank Markham (2003), Boolean Reasoning: The Logic of Boolean Equations, 1st edition, Kluwer Academic Publishers, Norwell, MA. 2nd edition, Dover Publications, Mineola, NY.
• Chang, C.C. and Keisler, H.J. (1973), Model Theory, North-Holland, Amsterdam, Netherlands.
• Kohavi, Zvi (1978), Switching and Finite Automata Theory, 1st edition, McGraw–Hill, 1970. 2nd edition, McGraw–Hill, 1978.
• Korfhage, Robert R. (1974), Discrete Computational Structures, Academic Press, New York, NY.
• Lambek, J. and Scott, P.J. (1986), Introduction to Higher Order Categorical Logic, Cambridge University Press, Cambridge, UK.
• Mendelson, Elliot (1964), Introduction to Mathematical Logic, D. Van Nostrand Company.

Related works

• Hofstadter, Douglas (1979). Gödel, Escher, Bach: An Eternal Golden Braid. Basic Books. ISBN 978-0-465-02656-2.

External links

• Klement, Kevin C. (2006), "Propositional Logic", in James Fieser and Bradley Dowden (eds.), Internet Encyclopedia of Philosophy, Eprint.
• Formal Predicate Calculus, contains a systematic formal development with axiomatic proof
• forall x: an introduction to formal logic, by P.D. Magnus, covers formal semantics and proof theory for sentential logic.
• Chapter 2 / Propositional Logic from Logic In Action
• Propositional sequent calculus prover on Project Nayuki. (note: implication can be input in the form !X|Y, and a sequent can be a single formula prefixed with > and having no commas)
• Propositional Logic - A Generative Grammar
• A Propositional Calculator that helps to understand simple expressions