Гипотетический силлогизм

Гипотетический силлогизм

Тип	Силлогизм
Поле	Пропозициональное исчисление Классическая логика Интуиционистская логика Большинство систем релевантной логики
Заявление	Всякий раз, когда случаи $P\to Q$, и $Q\to R$ появиться в строках доказательства , $P\to R$ можно разместить на следующей строке.
Символическое заявление	${\frac {P\to Q,Q\to R}{\therefore P\to R}}$

В классической логике гипотетический силлогизм — это действительная форма аргументации , дедуктивный силлогизм с условным утверждением для одной или обеих его посылок . Древние ссылки указывают на работы Теофраста и Евдема как первое исследование такого рода силлогизмов.

Типы

Гипотетические силлогизмы бывают двух типов: смешанные и чистые. Смешанный антецедент гипотетический силлогизм имеет две посылки: одно условное утверждение и одно утверждение, которое либо подтверждает, либо отрицает или следствие этого условного утверждения. Например,

Если П, то К.

П.

∴ В.

В этом примере первая посылка представляет собой условное утверждение, в котором «P» является антецедентом, а «Q» — следствием. Вторая посылка «подтверждает» антецедент. Вывод о том, что консеквент должен быть истинным, дедуктивно верен .

Смешанный гипотетический силлогизм имеет четыре возможных формы, две из которых действительны, а две другие недействительны. Правильный смешанный гипотетический силлогизм либо подтверждает антецедент ( modus ponens ), либо отрицает консеквент ( modus tollens ). Недействительный гипотетический силлогизм либо подтверждает консеквент (ошибка обратного ) , либо отрицает антецедент (ошибка обратного ) .

Существует четыре возможных формы смешанных гипотетических силлогизмов, две из которых действительны, а две - недействительны. Рассмотрение простого примера показывает, почему формы действительны или недействительны. Если «p» означает «Кандиру — рыба», а «q» означает «У Кандиру есть жабры», попытайтесь убедить себя, заменив эти утверждения на p и q в приведенной выше таблице.

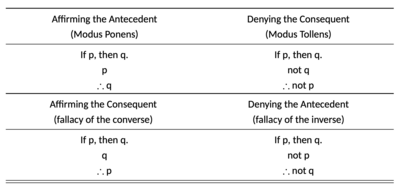
Чисто условными гипотетический силлогизм — это силлогизм, в котором как посылки, так и заключение являются утверждениями . Чтобы условие было действительным, антецедент одной посылки должен соответствовать следствию другой. Следовательно, кондиционалы содержат оставшееся антецедентом как антецедент и оставшееся следствие как следствие.

Если П, то К.

Если К, то Р.

∴ Если Р, то Р.

Пример на английском языке:

Если я не проснусь, то не смогу пойти на работу.

Если я не смогу выйти на работу, то мне не заплатят.

Поэтому, если я не проснусь, то мне не заплатят.

Пропозициональная логика

В логике высказываний гипотетический силлогизм — это название действующего правила вывода (часто сокращенно HS и иногда также называемого цепным аргументом , цепным правилом или принципом транзитивности импликации ). Правило можно сформулировать:

${\frac {P\to Q,Q\to R}{\therefore P\to R}}$

Другими словами, всякий раз, когда экземпляры " $P\to Q$", и " $Q\to R$"появляются в строках доказательства " , $P\to R$"можно разместить на следующей строке.

Применимость

Правило гипотетического силлогизма справедливо в классической логике , интуиционистской логике , большинстве систем релевантной логики и многих других системах логики. Однако это справедливо не для всех логик, включая, например, немонотонную логику , вероятностную логику и логику по умолчанию . Причина этого в том, что эта логика описывает отменяемые рассуждения , а условные выражения, которые появляются в контексте реального мира, обычно допускают исключения, предположения по умолчанию, условия при прочих равных условиях или просто простую неопределенность.

Пример взят из работы Эрнеста В. Адамса:

1. Если Джонс победит на выборах, Смит уйдет в отставку после выборов.
2. Если Смит умрет до выборов, Джонс победит на выборах.
3. Если Смит умрет до выборов, Смит уйдет в отставку после выборов.

Ясно, что (3) не следует из (1) и (2). (1) верно по умолчанию, но не выполняется в исключительных обстоятельствах смерти Смита. На практике реальные условные выражения всегда имеют тенденцию включать предположения или контексты по умолчанию, и может оказаться невозможным или даже невозможным указать все исключительные обстоятельства, при которых они могут оказаться неверными. По тем же причинам правило гипотетического силлогизма не действует для контрфактических кондиционалов .

Формальные обозначения

Правило вывода гипотетического силлогизма может быть записано в последовательной записи, что представляет собой специализацию правила отсечения:

${\frac {P\vdash Q\quad Q\vdash R}{P\vdash R}}$

где $\vdash$ является металогическим символом и $A\vdash B$ это означает, что $B$ является синтаксическим следствием $A$ в некоторой логической системе ;

и выражается в виде функциональной истинности тавтологии или теоремы логики высказываний :

$((P\to Q)\land (Q\to R))\to (P\to R)$

где $P$, $Q$, и $R$ Это предложения, выраженные в некоторой формальной системе .

Доказательство

Шаг	Предложение	Вывод
1	$P\to Q$	Данный
2	$Q\to R$	Данный
3	$P$	Предположение условного доказательства
4	$Q$	Режим настройки (1,3)
5	$R$	Режим настройки (2,4)
6	$P\to R$	Условное доказательство (3-5)

Альтернативные формы

Альтернативная форма гипотетического силлогизма, более полезная для классических систем исчисления высказываний с импликацией и отрицанием (т.е. без символа союза), следующая:

(HS1) $(Q\to R)\to ((P\to Q)\to (P\to R))$

Еще одна форма:

(HS2) $(P\to Q)\to ((Q\to R)\to (P\to R))$

Доказательство

Ниже приведен пример доказательства этих теорем в таких системах. Мы используем две из трех аксиом, используемых в одной из популярных систем, описанных Яном Лукасевичем .Доказательства опираются на две из трех аксиом этой системы:

(А1) $\phi \to \left(\psi \to \phi \right)$

(А2) $\left(\phi \to \left(\psi \rightarrow \xi \right)\right)\to \left(\left(\phi \to \psi \right)\to \left(\phi \to \xi \right)\right)$

Доказательство (HS1) заключается в следующем:

(1) $((p\to (q\to r))\to ((p\to q)\to (p\to r)))\to ((q\to r)\to ((p\to (q\to r))\to ((p\to q)\to (p\to r))))$ (пример (A1))

(2) $(p\to (q\to r))\to ((p\to q)\to (p\to r))$ (пример (A2))

(3) $(q\to r)\to ((p\to (q\to r))\to ((p\to q)\to (p\to r)))$ (из (1) и (2) по modus ponens )

(4) $((q\to r)\to ((p\to (q\to r))\to ((p\to q)\to (p\to r))))\to (((q\to r)\to (p\to (q\to r)))\to ((q\to r)\to ((p\to q)\to (p\to r))))$ (пример (A2))

(5) $((q\to r)\to (p\to (q\to r)))\to ((q\to r)\to ((p\to q)\to (p\to r)))$ (из (3) и (4) по modus ponens )

(6) $(q\to r)\to (p\to (q\to r))$ (пример (A1))

(7) $(q\to r)\to ((p\to q)\to (p\to r))$ (из (5) и (6) по modus ponens )

Доказательство (HS2) приведено здесь .

Как метатеорема

Всякий раз, когда у нас есть две теоремы вида $T_{1}=(Q\to R)$ и $T_{2}=(P\to Q)$, мы можем доказать $(P\to R)$ следующими шагами:

(1) $(Q\to R)\to ((P\to Q)\to (P\to R)))$ (пример доказанной выше теоремы)

(2) $Q\to R$ (пример (T1))

(3) $(P\to Q)\to (P\to R)$ (из (1) и (2) по modus ponens)

(4) $P\to Q$ (пример (T2))

(5) $P\to R$ (из (3) и (4) по modus ponens)

См. также

• Правдоподобное рассуждение
• Транзитивное отношение
• Тип силлогизма (дизъюнктивный, гипотетический, юридический, поли-, прослептический, квази-, статистический)

Внешние ссылки

• Индекс философии: гипотетический силлогизм