Правдоподобное рассуждение
Правдоподобное рассуждение — метод вывода новых выводов из данных известных посылок , метод, отличный от классических методов силлогистической аргументации аристотелевской двузначной логики . Силлогический стиль аргументации иллюстрируется часто цитируемым аргументом: «Все люди смертны, Сократ — человек, и, следовательно, Сократ смертен». Для сравнения рассмотрим утверждение: «Если идет дождь, то облачно». Единственный логический вывод, который можно сделать из этого, заключается в том, что «если не облачно, то и дождя нет». Но обычные люди в своей повседневной жизни пришли бы к выводу, что «если нет дождя, то облачность менее вероятна» или «если облачно, то дождь более правдоподобен». Невысказанные и бессознательно применяемые рассуждения, возможно, неверные, которые заставили людей прийти к своим выводам, типичны для правдоподобных рассуждений. [ нужна ссылка ] .
В качестве еще одного примера рассмотрим следующий сценарий: [1] «Предположим, в какую-то темную ночь полицейский идет по улице, очевидно, безлюдной; но вдруг он слышит охранную сигнализацию, смотрит через улицу и видит ювелирный магазин с разбитым окном. Затем через разбитое окно выползает человек в маске. окно, неся сумку, полную дорогих украшений. Полицейский сразу приходит к выводу, что этот человек крадет драгоценности». С помощью каких рассуждений полицейский приходит к такому выводу?
Очевидно, что вывод полицейского не был логическим выводом из доказательств. Всему может быть вполне обоснованное объяснение. Например, может быть, что этот человек был владельцем ювелирного магазина и возвращался домой с конкурса костюмированных костюмов, а ключа у него с собой не было. Но когда он проходил мимо своего магазина, проезжавший мимо грузовик бросил камень в окно; и он только защищал свою собственность, а не крал драгоценности. Каким бы ни был процесс рассуждений полицейского, он имеет определенную степень обоснованности. Доказательства не доказывали, что этот человек крал драгоценности, но делали это чрезвычайно правдоподобным. Это пример своего рода рассуждения, часто называемого правдоподобным рассуждением, которым большинство людей, как правило, очень владеют.
Рассуждения о правдоподобии в Древней Греции
[ редактировать ]В пятом веке до нашей эры [2] судебные ораторы на греческой Сицилии разработали метод успешного ведения дел в таких случаях, когда невозможно было предоставить ни очевидцев, ни письменные документы, ни другие подобные прямые доказательства. Они начали основывать свои аргументы на внутренней или внешней вероятности или правдоподобности своих утверждений. Этот новый способ аргументации обычно обозначался греческим термином eikós, термином, который по-разному переводился как сходство, правдоподобие, вероятность или правдоподобие. Успех аргументации зависит от ораторского мастерства говорящего, аргументы эйкоса часто обвиняют в недостаточной правдивости. Вот классический пример аргументации правдоподобными рассуждениями, представленный Аристотелем в его «Риторике»:
«Если обвиняемому не предъявлено обвинение – например, если слабого человека судят за насильственное нападение – защита заключается в том, что он вряд ли (eikós) совершил бы такое преступление. Но если он открыт для обвинения – это , если он сильный человек - защита по-прежнему заключается в том, что он вряд ли (eikós) сделал бы такое, поскольку он мог быть уверен, что люди подумают, что он (eikós) мог бы это сделать».
Говорят, что софисты, своего рода нищие академики, были экспертами в этом типе аргументации и, как говорят, обучали этим методам богатых молодых греков за огромную плату. Платон и Аристотель решительно осудили эти методы, и этот метод приобрел плохую репутацию. Софистические стили аргументации приравнивались к ошибочным аргументам.
Джордж Пойа и правдоподобные рассуждения
[ редактировать ]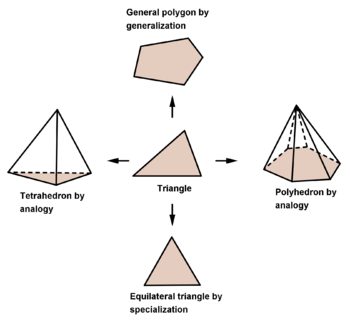
Джордж Пойя в своей двухтомной книге « Математика и правдоподобные рассуждения». [3] [4] представляет правдоподобные рассуждения как способ создания новых математических гипотез. Поля, «математическое доказательство — это демонстративное рассуждение, но индуктивное свидетельство физика, косвенное свидетельство юриста, документальное свидетельство историка и статистическое свидетельство экономиста — все это относится к правдоподобным рассуждениям». Намерение Пойи состоит в том, чтобы научить студентов искусству угадывания новых результатов в математике, для чего он использует такие понятия, как индукция и аналогия, как возможные источники правдоподобных рассуждений. Первый том книги посвящен обширному обсуждению этих идей с привлечением нескольких примеров из различных областей математики.
В предисловии к первому тому книги Поля призывает всех интересующихся математикой так: «Конечно, научимся доказывать, но научимся и гадать». П.Р. Халмош, рецензируя книгу, так резюмировал центральный тезис книги: «...хорошее предположение так же важно, как и хорошее доказательство». [5]
Том I: Индукция и аналогия в математике.
[ редактировать ]Пойа начинает том I с обсуждения индуктивных рассуждений (а не математической индукции ) как способа угадывания новых результатов. Он показывает, как случайные наблюдения нескольких результатов вида 4 = 2 + 2, 6 = 3 + 3, 8 = 3 + 5, 10 = 3 + 7 и т. д. могут побудить острый ум сформулировать гипотезу о том, что каждое четное число больше 4 можно представить как сумму двух нечетных простых чисел. Это известная гипотеза Гольдбаха . Первая задача первой главы — угадать правило, по которому выбираются последовательные члены следующей последовательности: 11, 31, 41, 61, 71, 101, 131, . . . В следующей главе методы обобщения, специализации и аналогии представлены как возможные стратегии правдоподобных рассуждений. В остальных главах эти идеи иллюстрируются обсуждением открытия нескольких результатов в различных областях математики, таких как теория чисел, геометрия и т. д., а также в физических науках.
Том II: Модели правдоподобных выводов
[ редактировать ]В этом томе делается попытка сформулировать определенные модели правдоподобных рассуждений. Также исследуются связи этих закономерностей с исчислением вероятностей. Также обсуждается их связь с математическими изобретениями и обучением. Ниже приведены некоторые модели правдоподобных выводов, обсуждаемые Пойей.
| Сл. Нет. | Посылка 1 | Посылка 2 | Посылка 3 | Правдоподобный вывод |
|---|---|---|---|---|
| 1 | А подразумевает Б | Б правда | - | Более заслуживающий доверия |
| 2 | A подразумевает B n +1 | B n +1 сильно отличается от проверенных ранее следствий B 1 , B 2 , . . , Б н А . | Б н +1 верно | Гораздо более заслуживающий доверия |
| 3 | A подразумевает B n +1 | B n +1 очень похоже на проверенные ранее следствия B 1 , B 2 , . . , Б н А . | Б н +1 верно | Просто немного более правдоподобно |
| 4 | А подразумевает Б | B само по себе очень маловероятно | Б правда | Гораздо более достоверный |
| 5 | А подразумевает Б | B вполне вероятно само по себе | Б правда | Просто немного более правдоподобно |
| 6 | Аналог Б. | Б правда | - | Более заслуживающий доверия |
| 7 | Аналог Б. | Б более достоверен | -- | Несколько более достоверный |
| 8 | А подразумевается Б | BБложь | -- | Менее заслуживающий доверия |
| 9 | А несовместимо с Б | BБложь | -- | Более заслуживающий доверия |
Характеристики правдоподобного аргумента
[ редактировать ]После детального анализа нескольких парадигматических примеров, взятых из древнегреческих текстов, Д. Уолтон и другие сформулировали следующие одиннадцать свойств как определяющие характеристики правдоподобных рассуждений. [6]
- Правдоподобное рассуждение исходит из предпосылок, которые более правдоподобны, к выводу, который был менее правдоподобным до появления правдоподобного аргумента.
- Что-то кажется правдоподобным, когда слушатели имеют в уме примеры.
- Правдоподобные рассуждения основаны на общеизвестных знаниях.
- Правдоподобное рассуждение невозможно опровергнуть .
- Правдоподобные рассуждения основаны на том, как обычно обстоят дела в знакомых ситуациях.
- Правдоподобные рассуждения можно использовать для заполнения неявных посылок в неполных аргументах.
- Правдоподобные рассуждения обычно основаны на явлениях восприятия.
- Стабильность — важная характеристика правдоподобных рассуждений.
- Правдоподобные рассуждения можно проверить и, таким образом, подтвердить или опровергнуть.
- Исследование правдоподобных рассуждений в диалоге — это способ его проверки.
- Правдоподобные рассуждения допускают степени путем проверки, но они отличаются от тех, которые используются в стандартных значениях вероятности и байесовских правилах, используемых в теории вероятности Паскаля.
Некоторые проблемы, связанные с формулировкой теории правдоподобных рассуждений
[ редактировать ]Аллан М. Коллинз , признанный авторитет в области интеллектуальных систем обучения и правдоподобных рассуждений, представив основную теорию логики правдоподобных рассуждений, выявил некоторые важные проблемы в формулировке такой теории. [7]
1. Представление степени веры.
Это проблема представления различий в силе убеждений, обозначенных фразами «полностью уверен» и «предполагаю».
2. Оценка силы аргументов.
Нам нужна вычислительная схема для расчета и сравнения различных уровней и силы убеждений.
3. Применение правил общего, но не универсального действия.
Стандартная логика оправдывает использование универсальных количественных правил; правила, которые верны всегда и без исключений. Многие выводы, основанные на здравом смысле, основаны на применении правил по умолчанию, которые справедливы в целом, но не всегда.
4. Избегание перечисления всех условий правила.
Часто случается, что правдоподобное правило здравого смысла, при внимательном рассмотрении, имеет почти неограниченное количество возможных типов исключений. Проблема рассмотрения всех этих потенциальных исключений известна как проблема квалификации .
5. Вывод из отсутствия информации.
Часто бывает разумно сделать вывод о том, что утверждение А ложно, на основании того факта, что никто не знает , что А истинно, или на основании того факта, что в формулировке задачи не утверждается, что оно истинно.
6. Ограничение объема умозаключений.
Многие интуитивно привлекательные наборы аксиом обладают тем свойством, что все первые несколько выводов кажутся разумными и приводят к разумным выводам, но по мере того, как выводы уходят все дальше и дальше от исходных аксиом, выводы кажутся все менее и менее разумными, и они в конечном итоге окажутся чистой ерундой.
7. Выводы с использованием расплывчатых понятий.
Выводы, предполагающие рассуждения вблизи границ расплывчатого понятия, часто бывают неопределенными.
8. Нахождение ожидаемой полезности.
Это проблема выбора между действиями, последствия которых неопределенны. В таком случае выбор может быть сделан на основе вероятности различных результатов и их желательности.
9. Вывод объяснения.
Сторонники здравого смысла пытаются объяснить причины, лежащие в основе их наблюдений. Если я замечу, что улица мокрая, я сделаю вывод, что шел дождь. Если я замечу, что тротуар не мокрый, я могу вместо этого решить, что дворники были здесь.
10. Вывод на основе схемы.
Многие полезные концепции здравого смысла соответствуют большим системам отношений, которые реализуются во многих отдельных случаях в мире. Такие концепции называются схемами или фреймами.
11. Вывод общего правила из примеров.
Люди всегда ищут общие правила, отражающие их наблюдения.
Ссылки
[ редактировать ]- ^ Э. Т. Джейнс (2003). Теория вероятностей: логика науки . Издательство Кембриджского университета. п. 3.
- ^ Манфред Краус. «Ранние греческие аргументы в пользу вероятности и точки соприкосновения в разногласиях» . В Х.В. Хансене; и др. (ред.). Разногласия и поиск точек соприкосновения . Виндзор, Онтарио: OSSA. стр. 1–11 . Проверено 21 февраля 2015 г.
- ^ Джордж Пойя (1954). Математика и правдоподобные рассуждения. Том I: Индукция и аналогия в математике . Издательство Принстонского университета.
- ^ Джордж Пойя (1954). Математика и правдоподобные рассуждения. Том II: Модели правдоподобных выводов . Издательство Принстонского университета.
- ^ П.Р. Халмош (1955). «Рецензия: Г. Поля, Математика и правдоподобные рассуждения» . Бюллетень Американского математического общества . 61 (3): 243–245. дои : 10.1090/s0002-9904-1955-09904-x . Проверено 21 февраля 2015 г.
- ^ Д. Уолтон; CW Тиндейл; Т.Ф. Гордон (2014). «Применение новейших методов аргументации к некоторым древним примерам правдоподобных рассуждений» (PDF) . Аргументация . 28 (1): 85–119. дои : 10.1007/s10503-013-9306-y . S2CID 17870888 . Архивировано из оригинала (PDF) 21 февраля 2015 года . Проверено 21 февраля 2015 г.
- ^ Аллан Коллинз (1989). «Логика правдоподобных рассуждений: основная теория» . Когнитивная наука . 13 : 1–49. дои : 10.1207/s15516709cog1301_1 .
Дальнейшее чтение
[ редактировать ]- Гленн Шафер, Джудея Перл (редакторы) (1990). Чтение по неопределенным рассуждениям . Морган Кауфманн. ISBN 9781558601253 .
{{cite book}}:|last1=имеет общее имя ( справка ) - Джонатан М. Борвейн, Дэвид Х. Бэйли (2004). Математика посредством эксперимента: правдоподобные рассуждения в 21 веке . АК Петерс. ISBN 9781568812113 .
- Иудея Перл (1988). Вероятностные рассуждения в интеллектуальных системах: сети правдоподобных выводов . Морган Кауфманн. ISBN 9781558604797 .