Алгебра Клиффорда
| Алгебраическая структура → Теория колец Теория колец |
|---|
В математике алгебра Клиффорда [а] — алгебра, порожденная векторным пространством квадратичной формы , и с единицей ассоциативная алгебра с дополнительной структурой выделенного подпространства. Как K -алгебры , они обобщают действительные числа , комплексные числа , кватернионы и некоторые другие гиперкомплексные системы счисления. [1] [2] Теория алгебр Клиффорда тесно связана с теорией квадратичных форм и ортогональных преобразований . Алгебры Клиффорда имеют важные приложения в различных областях, включая геометрию , теоретическую физику и цифровую обработку изображений . Они названы в честь английского математика Уильяма Кингдона Клиффорда (1845–1879).
Наиболее известные алгебры Клиффорда, ортогональные алгебры Клиффорда , также называются ( псевдо ) римановыми алгебрами Клиффорда , в отличие от симплектических алгебр Клиффорда . [б]
Введение и основные свойства [ править ]
Алгебра Клиффорда — это с единицей ассоциативная алгебра которая содержит и порождается векторным пространством V над полем K , где V снабжено квадратичной формой Q : V → K. , Алгебра Клиффорда Cl( V , Q ) является «самой свободной» унитарной ассоциативной алгеброй, порожденной V, подчиняющейся условию [с]
Когда V — конечномерное вещественное векторное пространство и , Cl Q невырождено ( V , Q ) может быть идентифицирован меткой Cl p , q ( R ) , указывающей, что V имеет ортогональный базис с p элементами с e i 2 = +1 , q с e i 2 = −1 , и где R указывает, что это алгебра Клиффорда над действительными числами; т.е. коэффициенты элементов алгебры являются действительными числами. Этот базис можно найти путем ортогональной диагонализации .
порожденную Свободную алгебру, V , можно записать как тензорную алгебру ⨁ n ≥0 V ⊗ ⋯ ⊗ V , то есть прямую сумму тензорного произведения n копий V по всем n . Следовательно, алгебру Клиффорда можно получить как фактор этой тензорной алгебры по двустороннему идеалу , порожденному элементами вида v ⊗ v − Q ( v )1 для всех элементов v ∈ V . Произведение, индуцированное тензорным произведением в факторалгебре, записывается с использованием сопоставления (например, uv ). Его ассоциативность следует из ассоциативности тензорного произведения.
Алгебра Клиффорда имеет выделенное подпространство V , являющееся образом отображения вложения . Такое подпространство, вообще говоря, не может быть определено однозначно, если только K -алгебра изоморфна алгебре Клиффорда.
Если 2 обратимо виде в основном поле K , то фундаментальное тождество, приведенное выше, можно переписать в
Квадратичные формы и алгебры Клиффорда в характеристике 2 представляют в этом отношении исключительный случай. В частности, если char( K ) = 2, неверно, что квадратичная форма обязательно или однозначно определяет симметричную билинейную форму, которая удовлетворяет условиям Q ( v ) = ⟨ v , v ⟩ , [3] Многие утверждения в этой статье включают условие, что характеристика не равна 2 , и являются ложными, если это условие удалено.
Как квантование внешней алгебры [ править ]
Алгебры Клиффорда тесно связаны с внешними алгебрами . Действительно, если Q = 0 то алгебра Клиффорда Cl( V , Q ) — это просто внешняя алгебра ⋀ V. , Всякий раз, когда 2 обратимо в основном поле K , существует канонический линейный изоморфизм между ⋀ V и Cl( V , Q ) . То есть они естественно изоморфны как векторные пространства, но с разными умножениями (в случае характеристики два они все еще изоморфны как векторные пространства, но не естественным образом). Умножение Клиффорда вместе с выделенным подпространством строго богаче внешнего произведения , поскольку оно использует дополнительную информацию, предоставляемую Q .
Алгебра Клиффорда является фильтрованной алгеброй ; соответствующая градуированная алгебра является внешней алгеброй.
Точнее, алгебры Клиффорда можно рассматривать как квантования (ср. квантовую группу ) внешней алгебры, точно так же, как алгебра Вейля является квантованием симметричной алгебры .
Алгебры Вейля и алгебры Клиффорда допускают дополнительную структуру *-алгебры и могут быть объединены как четные и нечетные члены супералгебры , как обсуждалось в CCR и CAR-алгебрах .
Универсальная недвижимость и строительство [ править ]
Пусть V — векторное пространство над полем K , и пусть Q : V → K — форма на V. квадратичная В большинстве представляющих интерес случаев поле K является либо полем действительных чисел R , либо полем комплексных чисел C , либо конечным полем .
Алгебра Клиффорда Cl( V , Q ) — это пара ( A , i ) , [д] [4] где A — с единицей ассоциативная алгебра над K , а i — линейное отображение i : V → Cl( V , Q ) , которое удовлетворяет i ( v ) 2 = Q ( v )1 для всех v в V , определенный следующим универсальным свойством : дана любая ассоциативная алгебра с единицей A над K и любое линейное отображение j : V → A такое, что
Квадратичная форма Q может быть заменена (не обязательно симметричной [5] ) билинейная форма ⟨⋅,⋅⟩ , обладающая свойством ⟨ v , v ⟩ = Q ( v ), v ∈ V , и в этом случае эквивалентным требованием к j является
Если характеристика поля не равна 2 , это может быть заменено эквивалентным требованием:
Алгебра Клиффорда, описанная выше, всегда существует и может быть построена следующим образом: начните с наиболее общей алгебры, содержащей V , а именно с тензорной алгебры T ( V ) , а затем обеспечьте фундаментальное тождество, взяв подходящее частное . В нашем случае мы хотим взять двусторонний идеал I Q в T ( V ), порожденный всеми элементами вида
Кольцевое произведение , унаследованное этим фактором, иногда называют произведением Клиффорда. [6] чтобы отличить его от внешнего произведения и скалярного произведения.
Тогда несложно показать, что Cl( V , Q ) содержит V и удовлетворяет указанному выше универсальному свойству, так что Cl уникален с точностью до единственного изоморфизма; таким образом, говорят об «алгебре Клиффорда Cl( V , Q ) . Из этой конструкции также следует, i инъективно что . Обычно отбрасывают i и рассматривают V как линейное подпространство Cl ( V , Q ) .
Универсальная характеризация алгебры Клиффорда показывает, что конструкция Cl( V , Q ) носит функториальный характер. А именно, Cl можно рассматривать как функтор из категории векторных пространств с квадратичными формами ( морфизмы которых представляют собой линейные отображения, сохраняющие квадратичную форму) в категорию ассоциативных алгебр. Свойство универсальности гарантирует, что линейные отображения между векторными пространствами (сохраняющие квадратичную форму) однозначно распространяются на гомоморфизмы алгебр между ассоциированными алгебрами Клиффорда.
Основа и размерность [ править ]
Поскольку V снабжен квадратичной формой Q отличной от 2 существуют базы для V. ортогональные , в характеристике , , Ортогональный базис — это такой базис, что для симметричной билинейной формы
Фундаментальное тождество Клиффорда означает, что для ортогонального базиса
Это делает манипуляции с ортогональными базисными векторами довольно простыми. Учитывая продукт различных можно привести их в стандартный порядок, включая общий знак , ортогональных базисных векторов V определяемый количеством парных замен, необходимых для этого (т. е. сигнатуру порядка перестановки ).
Если размерность V ( над K равна n и { e1 K ,..., e n } ортогональным базисом V , Q ) , то Cl( V , Q ) свободен над является с базисом
Пустой продукт ( k = 0 ) определяется как мультипликативный единичный элемент . Для каждого значения k существует n выбора k базисных элементов, поэтому общая размерность алгебры Клиффорда равна
: действительные и комплексные Клиффорда алгебры Примеры
Наиболее важными алгебрами Клиффорда являются алгебры над вещественными и комплексными векторными пространствами, снабженными невырожденными квадратичными формами .
из алгебр Clp A , q ( R ) и Cln из ( C ) изоморфна A или A ⊕ A , где — полное матричное кольцо с элементами R , C или H. Каждая Полную классификацию этих алгебр см. в разделе «Классификация алгебр Клиффорда» .
Действительные числа [ править ]
Алгебры Клиффорда также иногда называют геометрическими алгебрами , чаще всего над действительными числами.
Каждая невырожденная квадратичная форма в конечномерном вещественном векторном пространстве эквивалентна стандартной диагональной форме:
Стандартный базис { e 1 ..., en } R для , п , д состоит из n = p + q взаимно ортогональных векторов, p из которых квадрат к +1 и q из которых квадрат к −1 . Следовательно , из такого базиса алгебра Cl p , q ( R ) будет иметь p векторов, которые возводятся в квадрат +1 , и q векторов, которые возводятся в квадрат -1 .
Вот несколько случаев низкой размерности:
- Cl 0,0 ( R ) естественно изоморфен R , поскольку не существует ненулевых векторов.
- Cl 0,1 ( R ) — двумерная алгебра, порожденная e 1 , которая приводится в квадрат к −1 и алгебраически изоморфна C , полю комплексных чисел .
- Cl 0,2 ( R ) — четырехмерная алгебра, натянутая на {1, e 1 , e 2 , e 1 e 2 } . Последние три элемента квадратичны к −1 и антикоммутируют, поэтому алгебра изоморфна кватернионам H .
- Cl 0,3 ( R ) — 8-мерная алгебра, изоморфная прямой сумме H ⊕ H , расщепленным бикватернионам .
Комплексные числа [ править ]
Можно также изучать алгебры Клиффорда на комплексных векторных пространствах. Любая невырожденная квадратичная форма в комплексном векторном пространстве размерности n эквивалентна стандартной диагональной форме
Для первых нескольких случаев обнаруживается, что
- Cl 0 ( C ) ≅ C , комплексные числа
- Cl 1 ( C ) ≅ C ⊕ C , бикомплексные числа
- Cl 2 ( C ) ≅ M 2 ( C ) , бикватернионы
где M n ( C ) обозначает алгебру матриц размера n × n над C .
Примеры: построение кватернионов и двойных кватернионов [ править ]
Кватернионы [ править ]
Гамильтона В этом разделе кватернионы строятся как четная подалгебра алгебры Клиффорда Cl 3,0 ( R ) .
Пусть векторное пространство V — вещественное трехмерное пространство R 3 , а квадратичная форма — обычная квадратичная форма. Тогда для v , w в R 3 у нас есть билинейная форма (или скалярное произведение)
Обозначим набор ортогональных единичных векторов R 3 как { e 1 , e 2 , e 3 } , то произведение Клиффорда дает соотношения
Линейная комбинация элементов четной степени из Cl 3,0 ( R ) определяет четную подалгебру Cl [0]
3,0 ( R ) с общим элементом
3,0 ( R ) Гамильтона — вещественная алгебра кватернионов .
Чтобы увидеть это, вычислите
Двойные кватернионы [ править ]
В этом разделе двойственные кватернионы строятся как четная подалгебра алгебры Клиффорда вещественного четырехмерного пространства с вырожденной квадратичной формой. [7] [8]
Пусть векторное пространство V — вещественное четырехмерное пространство R 4 и пусть квадратичная форма Q — вырожденная форма, полученная из евклидовой метрики на R 3 . Для v , w в R 4 ввести вырожденную билинейную форму
Произведение Клиффорда векторов v и w определяется выражением
Обозначим набор взаимно ортогональных единичных векторов R 4 как { e1 произведение Клиффорда , e2 дает , e3 } , e4 то , соотношения
Общий элемент алгебры Клиффорда Cl( R 4 , d ) имеет 16 компонент. Линейная комбинация элементов четной степени определяет четную подалгебру Cl [0] ( Р 4 , d ) с общим элементом
Базисные элементы можно отождествить с базисными элементами кватернионов i , j , k и двойственной единицей ε как
0,3,1 ( R ) с двойственной алгеброй кватернионов.
Чтобы увидеть это, вычислите
Примеры: в маленьком размере [ править ]
Пусть K — любое поле характеристики, отличной от 2 .
Измерение 1 [ править ]
Для dim V = 1 , если Q имеет диагонализацию Diag( a ) , то есть существует ненулевой вектор x такой, что Q ( x ) = a , то Cl( V , Q ) алгебра-изоморфен K -алгебре порожденный элементом x , который удовлетворяет x 2 = a , квадратичная алгебра K [ X ] / ( X 2 - а ) .
В частности, если a = 0 (т. е. Q нулевая квадратичная форма), то Cl( V , Q ) алгебра-изоморфна алгебре двойственных чисел над K. —
Если a — ненулевой квадрат в K , то Cl( V , Q ≃ K ⊕ K. )
В противном случае Cl( V , Q ) изоморфно расширению квадратичного поля K ( √ a ) поля K .
Измерение 2 [ править ]
Для dim V = 2 , если Q имеет диагонализацию diag( a , b ) с ненулевыми a и b (которая всегда существует, если Q невырожден), то Cl( V , Q ) изоморфен K -алгебре, порожденной элементами x и y, удовлетворяющими x 2 = а и 2 знак равно б и ху = - yx .
Таким образом, Cl( V , Q ) изоморфна (обобщённой) алгебре кватернионов ( a , b ) K . Мы извлекаем кватернионы Гамильтона, когда a = b = −1 , поскольку H = (−1, −1) R .
В частном случае, если некоторый x в V удовлетворяет Q ( x ) = 1 , то Cl( V , Q ) ≃ M 2 ( K ) .
Свойства [ править ]
внешней алгеброй Связь с
Учитывая векторное пространство V , можно построить внешнюю алгебру ⋀ V , определение которой не зависит от какой-либо квадратичной формы V. на Оказывается, что если K не имеет характеристики 2 , то существует естественный изоморфизм между ⋀ V и Cl( V , Q ), рассматриваемыми как векторные пространства (и существует изоморфизм в характеристике два, который может быть неестественным). Это изоморфизм алгебры тогда и только тогда, когда Q = 0 . Таким образом, алгебру Клиффорда Cl( V , Q ) можно рассматривать как обогащение (или, точнее, квантование, см. введение) внешней алгебры на V с умножением, которое зависит от Q (все еще можно определить внешнее произведение независимо от Q ).
Самый простой способ установить изоморфизм — выбрать ортогональный базис { e1 расширить ,..., } en для V и его до базиса для Cl( V , Q ), как описано выше . Отображение Cl( V , Q ) → ⋀ V определяется уравнением
Если характеристика K . равна 0 , изоморфизм можно также установить путем антисимметризации Определим функции f k : V × ⋯ × V → Cl( V , Q ) формулой
Более сложный способ просмотреть взаимосвязь — построить фильтрацию на Cl( V , Q ) . Напомним, что тензорная алгебра T ( V ) имеет естественную фильтрацию: F 0 ⊂ Ф 1 ⊂ Ф 2 ⊂ ⋯ , где F к содержит суммы тензоров порядка ≤ k . Проецирование этого на алгебру Клиффорда дает фильтрацию на Cl( V , Q ) . Соответствующая градуированная алгебра
Оценка [ править ]
Далее предположим, что характеристика не равна 2 . [и]
Алгебры Клиффорда — это Z 2 - градуированные алгебры (также известные как супералгебры ). Действительно, линейное отображение на V, определенное как v ↦ − v ( отражение через начало координат ), сохраняет квадратичную форму Q и поэтому по универсальному свойству алгебр Клиффорда продолжается до автоморфизма алгебры
Поскольку α является инволюцией (т. е. оно квадратично до единицы ), можно разложить Cl( V , Q ) на положительные и отрицательные собственные пространства α
Поскольку α является автоморфизмом, отсюда следует, что:
Замечание . Алгебра Клиффорда не является Z -градуированной алгеброй, но является Z - фильтрованной , где Cl ≤ i ( V , Q ) — подпространство, натянутое на все произведения не более i элементов V .
Степень числа Клиффорда обычно относится к степени Z -градации.
Чётная подалгебра Cl [0] ( V , Q ) алгебры Клиффорда сама изоморфна алгебре Клиффорда. [ф] [г] Если V — ортогональная прямая сумма вектора a ненулевой нормы Q ( a ) и подпространства U , то Cl [0] ( V , Q ) изоморфен Cl( U , − Q ( a ) Q | U ) , где Q | U — это форма Q ограниченная U. , В частности, в отношении реалов это означает, что:
В отрицательно определенном случае это дает включение Cl 0, n −1 ( R ) ⊂ Cl 0, n ( R ) , которое расширяет последовательность
Аналогично, в комплексном случае можно показать, что четная подалгебра в Cl n ( C ) изоморфна Cl n −1 ( C ) .
Antiautomorphisms[editАнтиавтоморфизмы
Помимо автоморфизма α , существуют два антиавтоморфизма , которые играют важную роль в анализе алгебр Клиффорда. Напомним, что тензорная алгебра T ( V ) имеет антиавтоморфизм, который меняет порядок во всех произведениях векторов:
Обратите внимание, что все эти операции являются инволюциями . Можно показать, что они действуют как ±1 на элементы, чистые по Z -градации. Фактически все три операции зависят только от степени по модулю 4 . То есть, если x чист со степенью k , то
| к против 4 | 0 | 1 | 2 | 3 | … |
|---|---|---|---|---|---|
| + | − | + | − | (−1) к | |
| + | + | − | − | (−1) к ( к - 1)/2 | |
| + | − | − | + | (−1) к ( к + 1)/2 |
Клиффорда Скалярное произведение
Когда характеристика не равна 2 , квадратичная форма Q на V может быть расширена до квадратичной формы на всем Cl( V , Q ) (которую мы также обозначили Q ). Независимое от базиса определение одного такого расширения:
Соответствующая симметричная билинейная форма на Cl( V , Q ) определяется выражением
Оператор левого (соответственно правого) умножения Клиффорда на транспонирование a т элемента a является сопряженным к левому (соответственно правому) умножению Клиффорда на a относительно этого скалярного произведения. То есть,
Структура Клиффорда алгебр
В этом разделе мы предполагаем, что характеристика не равна 2 , векторное пространство V конечномерно и что соответствующая симметричная билинейная форма Q невырождена.
Центральная простая алгебра над K — это матричная алгебра над (конечномерной) алгеброй с делением с K. центром Например, центральные простые алгебры над вещественными числами являются матричными алгебрами либо над вещественными числами, либо над кватернионами.
- Если V имеет четную размерность, то ( V , Q ) — центральная простая алгебра над K. Cl
- Если V имеет четную размерность, то четная подалгебра Cl [0] ( V , Q ) — центральная простая алгебра над квадратичным расширением K или сумма двух изоморфных центральных простых алгебр K. над
- Если V имеет нечетную размерность, то Cl( V , Q ) является центральной простой алгеброй над квадратичным расширением K или суммой двух изоморфных центральных простых алгебр над K .
- Если V имеет нечетную размерность, то четная подалгебра Cl [0] ( V , Q ) центральная простая алгебра над K. —
Строение алгебр Клиффорда можно выяснить явно, используя следующий результат. Предположим, что U имеет четную размерность и неособую билинейную форму с дискриминантом d , и предположим, что V — другое векторное пространство с квадратичной формой. Алгебра Клиффорда группы U + V изоморфна тензорному произведению алгебр Клиффорда группы U и (−1) тусклый( U )/2 dV , которое представляет собой пространство V с его квадратичной формой, умноженной на (−1) тусклый( U )/2 д . В отношении реальных значений это, в частности, означает, что
Примечательно, что класс эквивалентности Мориты алгебры Клиффорда (ее теория представлений: класс эквивалентности категории модулей над ней) зависит только от сигнатуры ( p − q ) mod 8 . Это алгебраическая форма периодичности Ботта .
Группа Липшица [ править ]
Класс липшицевых групп ( он же [9] Группы Клиффорда или группы Клиффорда–Липшица) был открыт Рудольфом Липшицем . [10]
В этом разделе мы предполагаем, что конечномерна и квадратичная форма Q невырождена V .
Действие на элементы алгебры Клиффорда ее группы единиц может быть определено в терминах скрученного сопряжения: скрученное сопряжение с помощью x отображает y ↦ α ( x ) y x −1 , где α – основная инволюция, определенная выше .
Группа Липшица Γ определяется как набор обратимых элементов x , которые стабилизируют набор векторов относительно этого действия: [11] это означает, что для всех v в V мы имеем:
Эта формула также определяет действие группы Липшица на векторное пространство V , которое сохраняет квадратичную форму Q и, таким образом, дает гомоморфизм группы Липшица в ортогональную группу. Группа Липшица содержит все элементы r из V , для которых Q ( r ) обратимо в K , и они действуют на V посредством соответствующих отражений, которые переводят v в v - ( ⟨ r , v ⟩ + ⟨ v , r ⟩ ) / Q ( р ) . (В характеристике 2 они называются ортогональными трансвекциями, а не отражениями.)
Если V — конечномерное вещественное векторное пространство с невырожденной квадратичной формой, то группа Липшица отображается в ортогональную группу V относительно формы (по теореме Картана–Дьедонне ), а ядро состоит из ненулевых элементов поле К. Это приводит к точным последовательностям
По другим полям или с неопределенными формами отображение, как правило, не является включенным, и отказ фиксируется спинорной нормой.
Спинорная норма [ править ]
В произвольной характеристике спинорная норма Q определяется на группе Липшица формулой
Ненулевые элементы группы K имеют спинорную норму в группе ( K × ) 2 квадратов ненулевых элементов поля K . Итак, когда V конечномерно и неособо, мы получаем индуцированное отображение ортогональной группы V в группу K × / ( К × ) 2 , также называемая спинорной нормой. Спинорная норма отражения о r ⊥ , для любого вектора r имеет образ Q ( r ) в K × / ( К × ) 2 , и это свойство однозначно определяет его на ортогональной группе. Это дает точные последовательности:
Заметим, что в характеристике 2 группа {±1} имеет всего один элемент.
С точки зрения когомологий Галуа алгебраических групп , спинорная норма является связующим гомоморфизмом на когомологиях. Записывая µ 2 для алгебраической группы квадратных корней из 1 (над полем характеристики, отличной от 2, это примерно то же самое, что двухэлементная группа с тривиальным действием Галуа), короткая точная последовательность
0-я группа когомологий Галуа алгебраической группы с коэффициентами из K — это просто группа K -значных точек: H 0 ( грамм ; K ) знак равно грамм ( K ) , и ЧАС 1 (μ 2 ; K ) ≅ K × / ( К × ) 2 , который восстанавливает предыдущую последовательность
Группы вращений и штифтов [ править ]
В этом разделе мы предполагаем, что V конечномерно и его билинейная форма неособа.
Группа контактов Pin V ( K ) является подгруппой группы Липшица Γ элементов спинорной нормы 1 , и аналогично группа спина Spin V ( K ) является подгруппой элементов инварианта Диксона 0 в Pin V ( K ) . Когда характеристика не равна 2 , это элементы определителя 1 . Группа вращения обычно имеет индекс 2 в группе контактов.
Напомним из предыдущего раздела, что существует гомоморфизм группы Липшица в ортогональную группу. Мы определяем специальную ортогональную группу как образ Γ 0 . Если K не имеет характеристики 2, то это просто группа элементов ортогональной группы определителя 1 . Если K действительно имеет характеристику 2 , то все элементы ортогональной группы имеют определитель 1 , а специальная ортогональная группа представляет собой набор элементов инварианта Диксона 0 .
Существует гомоморфизм группы штифтов в ортогональную группу. Образ состоит из элементов спинорной нормы 1 ∈ K × / ( К × ) 2 . Ядро состоит из элементов +1 и −1 и имеет порядок 2, если K не имеет характеристики 2 . Аналогично существует гомоморфизм группы Spin в специальную ортогональную группу V .
В общем случае, когда V является положительно или отрицательно определенным пространством над действительными числами, группа спинов отображается в специальную ортогональную группу и является односвязной, когда V имеет размерность не менее 3 . Далее ядро этого гомоморфизма состоит из 1 и −1 . Итак, в этом случае спиновая группа Spin( n ) является двойным покрытием SO( n ) . Однако обратите внимание, что простая связность спиновой группы в общем случае неверна: если V есть R п , д если p и q оба не менее 2 , то спиновая группа не является односвязной. В этом случае алгебраическая группа Spin p , q односвязна как алгебраическая группа, хотя ее группа вещественнозначных точек Spin p , q ( R ) не является односвязной. Это довольно тонкий момент, который окончательно сбил с толку авторов как минимум одной стандартной книги о спиновых группах. [ который? ]
Спиноры [ править ]
Алгебры Клиффорда Cl p , q ( C ) с p + q = 2 n четными являются матричными алгебрами, имеющими комплексное представление размерности 2 . н . Ограничивая группу Pin p , q ( R ), мы получаем комплексное представление группы Pin той же размерности, называемое спиновым представлением . Если мы ограничим это спиновой группой Spin p , q ( R ), тогда она распадается как сумма двух представлений половинного спина (или представлений Вейля ) размерности 2. п -1 .
Если p + q = 2 n + 1 нечетно, то алгебра Клиффорда Cl p , q ( C ) представляет собой сумму двух матричных алгебр, каждая из которых имеет представление размерности 2 н , и это также оба представления группы контактов Pin p , q ( R ) . При ограничении на спиновую группу Spin p , q ( R ) они становятся изоморфными, поэтому спиновая группа имеет комплексное спинорное представление размерности 2. н .
В более общем смысле, спинорные группы и группы штифтов над любым полем имеют схожие представления, точная структура которых зависит от структуры соответствующих алгебр Клиффорда : всякий раз, когда алгебра Клиффорда имеет фактор, который является матричной алгеброй над некоторой алгеброй с делением, мы получаем соответствующее представление группы штифтов и спинов над этой алгеброй с делением.Примеры реалов см. в статье о спинорах .
Настоящие спиноры [ править ]
Чтобы описать реальные представления спина, нужно знать, как спиновая группа располагается внутри своей алгебры Клиффорда. Группа контактов , Pin p , q — это набор обратимых элементов в Cl p , q , которые можно записать как произведение единичных векторов:
Пусть α : Cl → Cl — автоморфизм, задаваемый отображением v ↦ − v, действующим на чистые векторы. Тогда, в частности, Spin p , q — подгруппа Pin p , q , элементы которой фиксированы α . Позволять
п , д .
Неприводимые представления Cl p , q ограничиваются представлениями группы выводов. И наоборот, поскольку группа контактов генерируется единичными векторами, все ее неприводимые представления индуцируются таким образом. Таким образом, два представления совпадают. По тем же причинам неприводимые представления спина совпадают с неприводимыми представлениями Cl [0]
п , д .
Для классификации пин-представлений достаточно обратиться лишь к классификации алгебр Клиффорда . Чтобы найти представления спина (которые являются представлениями четной подалгебры), можно сначала использовать любой из изоморфизмов (см. Выше)
Приложения [ править ]
Дифференциальная геометрия [ править ]
Одно из основных применений внешней алгебры находится в дифференциальной геометрии , где она используется для определения пучка дифференциальных форм на гладком многообразии . В случае ( псевдо- ) риманова многообразия касательные пространства снабжены естественной квадратичной формой, индуцированной метрикой . Таким образом, можно определить расслоение Клиффорда аналогично внешнему расслоению . Это имеет ряд важных приложений в римановой геометрии . Возможно, более важным является связь со спиновым многообразием , связанным с ним спинорным расслоением и спином. с коллекторы.
Физика [ править ]
Алгебры Клиффорда имеют множество важных приложений в физике. Физики обычно считают алгеброй Клиффорда алгебру, базис которой порождается матрицами γ 0 , ..., γ 3 , называемыми матрицами Дирака , которые обладают свойством
1,3 ( R ) которого , комплексификация есть Cl
1,3 ( R ) C , которая по классификации алгебр Клиффорда изоморфна алгебре 4×4 комплексных матриц Cl4 размера ( C ) ≈ M4 ( C ) . Однако лучше всего сохранить обозначение Cl
1,3 ( R ) C , поскольку любое преобразование, которое переводит билинейную форму в каноническую форму, не является преобразованием Лоренца основного пространства-времени.
Таким образом, алгебра пространства-времени Клиффорда, используемая в физике, имеет более структуру, чем Cl 4 ( C ) . Кроме того, он имеет ряд предпочтительных преобразований – преобразований Лоренца. Необходимость комплексификации для начала зависит частично от используемых соглашений и частично от того, насколько много мы хотим включить напрямую, но комплексификация чаще всего необходима в квантовой механике, где спиновое представление алгебры Ли ( 1, 3) находится внутри алгебра Клиффорда обычно требует комплексной алгебры Клиффорда. Для справки: спиновая алгебра Ли имеет вид
Это соответствует соглашению (3, 1) , поэтому подходит для Cl.
3,1 ( Р ) С . [12]
Матрицы Дирака были впервые записаны Полем Дираком , когда он пытался написать релятивистское волновое уравнение первого порядка для электрона и дать явный изоморфизм алгебры Клиффорда алгебре комплексных матриц. Результат был использован для определения уравнения Дирака и введения оператора Дирака . Вся алгебра Клиффорда проявляется в квантовой теории поля в виде билинейеров поля Дирака .
Использование алгебр Клиффорда для описания квантовой теории было предложено, среди прочего, Марио Шенбергом . [я] Дэвидом Хестенсом в терминах геометрического исчисления , Дэвидом Бомом и Бэзилом Хили и его сотрудниками в форме иерархии алгебр Клиффорда , а также Элио Конте и др. [13] [14]
Компьютерное зрение [ править ]
Алгебры Клиффорда применялись в задаче распознавания и классификации действий в компьютерном зрении . Родригес и др. [15] предложить встраивание Клиффорда для обобщения традиционных фильтров MACH на видео (3D пространственно-временной объем) и векторные данные, такие как оптический поток . Векторные данные анализируются с использованием преобразования Фурье Клиффорда . На основе этих векторов синтезируются фильтры действий в области Фурье Клиффорда и распознавание действий осуществляется с использованием корреляции Клиффорда. Авторы демонстрируют эффективность встраивания Клиффорда, распознавая действия, обычно выполняемые в классических художественных фильмах и спортивных телетрансляциях.
Обобщения [ править ]
- Хотя эта статья посвящена алгебре Клиффорда векторного пространства над полем, определение без изменений распространяется на модуль над любым ассоциативным коммутативным кольцом с единицей. [Дж]
- Алгебры Клиффорда могут быть обобщены до формы степени выше квадратичной в векторном пространстве. [16]
См. также [ править ]
- Алгебра физического пространства
- Строительство Кэли – Диксона
- Классификация алгебр Клиффорда
- Анализ Клиффорда
- Модуль Клиффорда
- Сложная спиновая структура
- Оператор Дирака
- Внешняя алгебра
- Личность Фирца
- Гамма-матрицы
- Обобщенная алгебра Клиффорда
- Геометрическая алгебра
- Гамма-матрицы более высокой размерности
- Гиперкомплексное число
- Октонион
- Паравектор
- Кватернион
- Спиновая группа
- Спиновая структура
- Спинор
- Спинорное расслоение
Примечания [ править ]
- ^ Также известна как геометрическая алгебра (особенно над действительными числами).
- ^ См. например. Озевич и Ситарчик, 1992 г.
- ^ Математики, которые работают с реальными алгебрами Клиффорда и предпочитают положительно определенные квадратичные формы (особенно те, кто работает в теории индексов ), иногда используют другой выбор знака в фундаментальном тождестве Клиффорда. То есть они принимают v 2 знак равно - Q ( v ) . необходимо заменить Q на – Q. При переходе от одного соглашения к другому
- ^ Ваз и да Роша 2016 проясняют, что карта i ( γ в цитате здесь) включена в структуру алгебры Клиффорда, определяя ее как «Пара ( A , γ ) является алгеброй Клиффорда для квадратичного пространства ( V , g ), когда A алгебра с помощью { γ ( v ) | v ∈ V } и { a 1 A | R ( порождается как } , и γ удовлетворяет условию γ v ) γ ( u ) + γ ( u ) γ ( v ) знак равно 2 г ( v , ты ) для всех v , ты ∈ V ».
- ^ Таким образом, алгебра K [ Z / 2 Z ] полупроста групповая , а алгебра Клиффорда распадается на собственные пространства основной инволюции.
- ^ Технически, она не имеет полной структуры алгебры Клиффорда без обозначенного векторного подпространства и поэтому изоморфна как алгебра, но не как алгебра Клиффорда.
- ^ Мы по-прежнему предполагаем, что характеристика не равна 2 .
- ^ Обратное верно при использовании альтернативного соглашения о знаках (-) для алгебр Клиффорда: более важным является сопряжение. В общем, значения спряжения и транспонирования меняются местами при переходе от одного соглашения о знаках к другому. Например, в используемом здесь соглашении обратный вектор определяется как v −1 = v т / Q ( v ), тогда как в соглашении (−) он определяется как v −1 знак равно v / Q ( v ) .
- ^ См. ссылки на статьи Шенберга 1956 и 1957 годов, описанные в разделе «Алгебра Грассмана – Шенберга G n » журнала Bolivar 2001.
- ^ См. например. Озевич и Ситарчик, 1992 г.
Цитаты [ править ]
- ^ Клиффорд 1873 , стр. 381–395.
- ^ Клиффорд 1882 г.
- ^ Лунесто 1993 , стр. 155–156.
- ^ Lounesto 1996 , стр. 3–30 или сокращенная версия.
- ^ Лунесто 1993
- ^ Лунесто 2001 , §1.8
- ^ Маккарти 1990 , стр. 62–65.
- ^ Боттема и Рот, 2012 г.
- ^ Ваз и да Роча 2016 , с. 126
- ^ Лунесто 2001 , §17.2
- ^ Первасс 2009 , §3.3.1
- ^ Вайнберг 2002
- ^ Конте 2007
- ^ Конте 2012
- ^ Родригес и Шах, 2008 г.
- ^ Хайле 1984
Ссылки [ править ]
- Боливар, АО (2001), «Классический предел фермионов в фазовом пространстве», J. Math. Физ. , 42 (9): 4020–4030, Bibcode : 2001JMP....42.4020B , doi : 10.1063/1.1386411
- Боттема, О.; Рот, Б. (2012) [1979]. Теоретическая кинематика . Дувр. ISBN 978-0-486-66346-3 .
- Бурбаки, Николя (1988), Алгебра , Springer-Verlag , ISBN 978-3-540-19373-9 , раздел IX.9.
- Клиффорд, WK (1873 г.). «Предварительный набросок бикватернионов». Учеб. Лондонская математика. Соц . 4 .
- Клиффорд, WK (1882 г.). Такер, Р. (ред.). Математические статьи . Лондон: Макмиллан.
- Карнахан, С., Заметки семинара Борчердса, необрезанный, неделя 5 , Спиноры и алгебры Клиффорда
- Конте, Элио (14 ноября 2007 г.). «Квантовая интерпретация и решение парадокса Эйнштейна, Подольского и Розена в квантовой механике». arXiv : 0711.2260 [ квант-ф ].
- Конте, Элио (2012), «О некоторых соображениях математической физики: можем ли мы идентифицировать алгебру Клиффорда как общую алгебраическую структуру для классической диффузии и уравнений Шредингера?», Adv. Исследования Теор. Физ. , 6 (26): 1289–1307
- Гарлинг, DJH (2011), Алгебры Клиффорда. Введение , Студенческие тексты Лондонского математического общества, том. 78, Издательство Кембриджского университета , ISBN 978-1-107-09638-7 , Збл 1235.15025
- Хейл, Даррелл Э. (декабрь 1984 г.). «Об алгебре Клиффорда двоичной кубической формы». Американский журнал математики . 106 (6). Издательство Университета Джонса Хопкинса: 1269–1280. дои : 10.2307/2374394 . JSTOR 2374394 .
- Джаганнатан, Р. (2010), Об обобщенных алгебрах Клиффорда и их физических приложениях , arXiv : 1005.4300 , Bibcode : 2010arXiv1005.4300J
- Лам, Цит-Юэнь (2005), Введение в квадратичные формы над полями , Аспирантура по математике , том. 67, Американское математическое общество , ISBN. 0-8218-1095-2 , МР 2104929 , Збл 1068.11023
- Лоусон, Х. Блейн; Майкельсон, Мария-Луиза (1989), Спиновая геометрия , Princeton University Press , ISBN 978-0-691-08542-5 . Расширенный учебник по алгебрам Клиффорда и их приложениям к дифференциальной геометрии.
- Лунесто, Пертти (1993), З. Озиевич; Б. Янцевич; А. Боровец (ред.), «Что такое бивектор?», Спиноры, твисторы, алгебры Клиффорда и квантовые деформации , Фундаментальные теории физики: 153–158.
- Лунесто, Пертти (1996), «Контрпримеры в алгебрах Клиффорда с CLICAL», Алгебры Клиффорда с числовыми и символическими вычислениями , стр. 3–30, doi : 10.1007/978-1-4615-8157-4_1 , ISBN 978-1-4615-8159-8
- Лунесто, Пертти (2001), алгебры и спиноры Клиффорда , Cambridge University Press , ISBN 978-0-521-00551-7
- Маккарти, Дж. М. (1990). Введение в теоретическую кинематику . МТИ Пресс. ISBN 978-0-262-13252-7 .
- Озиевич, З.; Ситарчик, С. (1992). «Параллельное рассмотрение римановых и симплектических алгебр Клиффорда» . В Микали, А.; Буде, Р.; Хельмстеттер, Дж. (ред.). Алгебры Клиффорда и их приложения в математической физике . Клювер. п. 83. ИСБН 0-7923-1623-1 .
- Первасс, Кристиан (2009), Геометрическая алгебра с приложениями в технике , Springer Science & Business Media, Bibcode : 2009gaae.book.....P , ISBN 978-3-540-89068-3
- Портеус, Ян Р. (1995), Алгебры Клиффорда и классические группы , Cambridge University Press , ISBN 978-0-521-55177-9
- Родригес, Микель; Шах, М. (2008). «Действие MACH: пространственно-временной фильтр максимальной средней высоты корреляции для классификации действий». Компьютерное зрение и распознавание образов (CVPR) .
- Сильвестр, Дж. Дж. (1882), Слово о нонионах , Проспекты Университета Джона Хопкинса, том. I, стр. 241–2, hdl : 1774,2/32845 ; там же II (1883) 46; там же III (1884) 7–9. Краткое изложение в «Сборнике статей по математике Джеймса Джозефа Сильвестра» (издательство Кембриджского университета, 1909 г.), т. III . онлайн и дальше .
- Ваз, Дж.; да Роша, Р. (2016), Введение в алгебры и спиноры Клиффорда , Oxford University Press , Bibcode : 2016icas.book.....V , ISBN 978-0-19-878292-6
- Вайнберг, С. (2002), Квантовая теория полей , том. 1, Издательство Кембриджского университета , ISBN 0-521-55001-7
Дальнейшее чтение [ править ]
- Кнус, Макс-Альберт (1991), Квадратичные и эрмитовы формы над кольцами , Основные учения математических наук, том. 294, Springer-Verlag , номер документа : 10.1007/978-3-642-75401-2 , ISBN. 3-540-52117-8 , МР 1096299 , Збл 0756.11008
Внешние ссылки [ править ]
- «Алгебра Клиффорда» , Математическая энциклопедия , EMS Press , 2001 [1994]
- Запись Planetmath об алгебрах Клиффорда. Архивировано 15 апреля 2005 г. в Wayback Machine.
- История алгебр Клиффорда (непроверенная)
- Джон Баэз об алгебрах Клиффорда
- Алгебра Клиффорда: визуальное введение






![{\displaystyle \mathbb {Z} [1/p]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab7b4e5c999e46c7614c3264b1d80708f4363433)








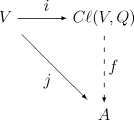





































![{\displaystyle \operatorname {Cl} (V,Q)=\operatorname {Cl} ^{[0]}(V,Q)\oplus \operatorname {Cl} ^{[1]}(V,Q)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34698bf037377a2edaee78a3dd92e84f286c2065)
![{\displaystyle \operatorname {Cl} ^{[i]}(V,Q)=\left\{x\in \operatorname {Cl} (V,Q)\mid \alpha (x)=(-1)^ {i}x\вправо\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6902ed1e7c0361df4271000a56e7b76c029990e)
![{\displaystyle \operatorname {Cl} ^{[i]}(V,Q)\operatorname {Cl} ^{[j]}(V,Q)=\operatorname {Cl} ^{[i+j]}(V,Q)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23cb5e567bcf36cd16a56b991facede0ba9d69c9)

![{\displaystyle \operatorname {Cl} _{p,q}^{[0]}(\mathbf {R})\cong {\begin{cases}\operatorname {Cl} _{p,q-1}(\ mathbf {R} )&q>0\\\operatorname {Cl} _{q,p-1}(\mathbf {R} )&p>0\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55a73e10c8b20fb6d947e7f9a0b81288e3b7408c)























![{\displaystyle \operatorname {Cl} _{p,q}^{[0]}=\{x\in \operatorname {Cl} _{p,q}\mid \alpha (x)=x\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e214b8b455c0610747a107adad00e2c3573ca61)
![{\displaystyle \operatorname {Cl} _{p,q}^{[0]}\approx \operatorname {Cl} _{p,q-1},{\text{ for }}q>0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4add0c62afed4cf6f1c8d379c39b3f15e6f031d1)
![{\displaystyle \operatorname {Cl} _{p,q}^{[0]}\approx \operatorname {Cl} _{q,p-1},{\text{for }}p>0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79f190bb97289dfe3a50eb02e74e3cffe2663246)

![{\displaystyle {\begin{aligned}\sigma ^{\mu \nu }&=-{\frac {i}{4}}\left[\gamma ^{\mu },\,\gamma ^{\nu }\right],\\\left[\sigma ^{\mu \nu },\,\sigma ^{\rho \tau }\right]&=i\left(\eta ^{\tau \mu }\ сигма ^{\rho \nu }+\eta ^{\nu \tau }\sigma ^{\mu \rho }-\eta ^{\rho \mu }\sigma ^{\tau \nu }-\eta ^ {\nu \rho }\sigma ^{\mu \tau }\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b5881264248f2f1787c4d1d2c4de84dd1678754)






