Змеиная лемма

Лемма о змее — инструмент, используемый в математике , особенно в гомологической алгебре , для построения длинных точных последовательностей . Лемма о змее действительна в каждой абелевой категории и является важнейшим инструментом в гомологической алгебре и ее приложениях, например, в алгебраической топологии . Гомоморфизмы, построенные с его помощью, обычно называют связующими гомоморфизмами .

Заявление

В абелевой категории (такой как категория абелевых групп или категория векторных пространств над заданным полем ) рассмотрим коммутативную диаграмму :

где строки представляют собой точные последовательности , а 0 — нулевой объект .

Тогда существует точная последовательность, ядра и коядра a связывающая , b и c :

$\ker a~{\color {Gray}\longrightarrow }~\ker b~{\color {Gray}\longrightarrow }~\ker c~{\overset {d}{\longrightarrow }}~\operatorname {coker} a~{\color {Gray}\longrightarrow }~\operatorname {coker} b~{\color {Gray}\longrightarrow }~\operatorname {coker} c$

где d — гомоморфизм, известный как соединительный гомоморфизм .

Более того, если морфизм f является мономорфизмом , то мономорфизмом является также и морфизм $\ker a~{\color {Gray}\longrightarrow }~\ker b$, и если g' является эпиморфизмом , то также $\operatorname {coker} b~{\color {Gray}\longrightarrow }~\operatorname {coker} c$.

Коядра здесь: $\operatorname {coker} a=A'/\operatorname {im} a$, $\operatorname {coker} b=B'/\operatorname {im} b$, $\operatorname {coker} c=C'/\operatorname {im} c$.

Объяснение названия

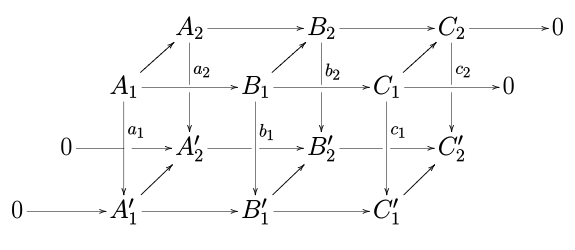
Чтобы увидеть, откуда лемма о змее получила свое название, разверните диаграмму выше следующим образом:

и тогда точную последовательность, которая является заключением леммы, можно изобразить на этой расширенной диаграмме в форме перевернутой буквы S скользящей змеи .

Создание карт

Анимация построения карты d

Отображения между ядрами и отображения между коядрами естественным образом индуцируются заданными (горизонтальными) отображениями в силу коммутативности диаграммы. Точность двух индуцированных последовательностей прямым образом следует из точности строк исходной диаграммы. Важным утверждением леммы является то, что существует связующий гомоморфизм d , завершающий точную последовательность.

В случае абелевых групп или модулей над некоторым кольцом отображение d можно построить следующим образом:

Выберите элемент x в ker c и просмотрите его как элемент C ; поскольку g сюръективен g , существует y в B такой, что ( y ) = x . Из-за коммутативности диаграммы имеем g' ( b ( y )) = c ( g ( y )) = c ( x ) = 0 (поскольку x находится в ядре c ), и, следовательно, b ( y ) находится в ядре g' . Поскольку нижняя строка точна, мы находим элемент z в A' с f '( z ) = b ( y ). z уникальна в силу инъективности f '. Затем мы определяем d ( x ) = z + im ( a ). Теперь нужно проверить, что d корректно определена (т. е. d ( x ) зависит только от x , а не от выбора y ), что это гомоморфизм и что полученная длинная последовательность действительно точна. Точность можно легко проверить путем поиска диаграмм (см. доказательство леммы 9.1 в ).

Как только это будет сделано, теорема будет доказана для абелевых групп или модулей над кольцом. В общем случае аргумент можно перефразировать, используя свойства стрелок и отмены вместо элементов. В качестве альтернативы можно воспользоваться теоремой вложения Митчелла .

Естественность

В приложениях часто приходится показывать, что длинные точные последовательности являются «естественными» (в смысле естественных преобразований ). Это следует из естественности последовательности, порождаемой леммой о змее.

Если

является коммутативной диаграммой с точными строками, то лемму о змее можно применить дважды, к «передней» и «обратной сторонам», что даст две длинные точные последовательности; они связаны коммутативной диаграммой вида

Пример

Позволять $k$ быть полем, $V$ быть $k$-векторное пространство. $V$ является $k[t]$-модуль по $t:V\to V$ будучи $k$-линейное преобразование, поэтому мы можем тензорировать $V$ и $k$ над $k[t]$.

$V\otimes _{k[t]}k=V\otimes _{k[t]}(k[t]/(t))=V/tV=\operatorname {coker} (t).$

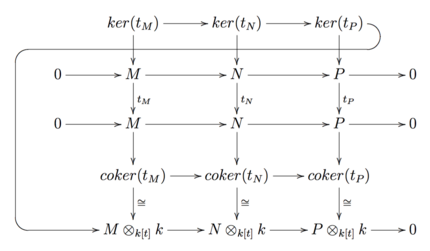
Учитывая короткую точную последовательность $k$-векторные пространства $0\to M\to N\to P\to 0$, мы можем вызвать точную последовательность $M\otimes _{k[t]}k\to N\otimes _{k[t]}k\to P\otimes _{k[t]}k\to 0$ по правильной точности тензорного произведения. Но последовательность $0\to M\otimes _{k[t]}k\to N\otimes _{k[t]}k\to P\otimes _{k[t]}k\to 0$ не точно в общем. Отсюда возникает закономерный вопрос. Почему эта последовательность не точна?

Согласно диаграмме выше, мы можем вызвать точную последовательность $\ker(t_{M})\to \ker(t_{N})\to \ker(t_{P})\to M\otimes _{k[t]}k\to N\otimes _{k[t]}k\to P\otimes _{k[t]}k\to 0$ применив лемму о змее. Таким образом, лемма о змее, если быть точным, отражает несостоятельность тензорного произведения.

В категории группы

В то время как многие результаты гомологической алгебры, такие как лемма о пяти или лемме о девяти , справедливы как для абелевых категорий, так и для категорий групп, лемма о змее — нет. Действительно, произвольных коядер не существует. Однако можно заменить коядра (левыми) смежными классами $A'/\operatorname {im} a$, $B'/\operatorname {im} b$, и $C'/\operatorname {im} c$.Тогда связующий гомоморфизм еще можно определить и записать последовательность, как в формулировке леммы о змее. Это всегда будет цепной комплекс, но он может быть не точным. Однако точность можно утверждать, когда вертикальные последовательности на диаграмме точны, то есть когда образы a , b и c являются нормальными подгруппами .

Контрпример

Рассмотрим знакопеременную группу $A_{5}$: содержит подгруппу, изоморфную симметрической группе $S_{3}$, что, в свою очередь, можно записать как полупрямое произведение циклических групп : $S_{3}\simeq C_{3}\rtimes C_{2}$. В результате получается следующая диаграмма с точными строками:

${\begin{matrix}&1&\to &C_{3}&\to &C_{3}&\to 1\\&\downarrow &&\downarrow &&\downarrow \\1\to &1&\to &S_{3}&\to &A_{5}\end{matrix}}$

Обратите внимание, что средний столбец неточен: $C_{2}$ не является нормальной подгруппой полупрямого произведения.

С $A_{5}$ прост , правая вертикальная стрелка имеет тривиальное коядро. При этом факторгруппа $S_{3}/C_{3}$ изоморфен $C_{2}$. Таким образом, последовательность в формулировке леммы о змее имеет вид

$1\longrightarrow 1\longrightarrow 1\longrightarrow 1\longrightarrow C_{2}\longrightarrow 1$,

что на самом деле не является точным.

В популярной культуре

Доказательству леммы о змее учит героиня Джилл Клейбург в самом начале фильма 1980 года « Это моя очередь» .

См. также

• Зигзагообразная лемма

Ссылки

• Ланг, Серж (2002). «III §9 Лемма о змее» . Алгебра (3-е изд.). Спрингер. стр. 157–9. ISBN  978-0-387-95385-4 .
• Атья, Миссури ; Макдональд, И.Г. (1969). Введение в коммутативную алгебру . Аддисон-Уэсли. ISBN  0-201-00361-9 .
• Хилтон, П.; Штамбах, У. (1997). Курс гомологической алгебры . Тексты для аспирантов по математике . Спрингер. п. 99. ИСБН  0-387-94823-6 .

Внешние ссылки

• Вайсштейн, Эрик В. «Лемма о змее» . Математический мир .
• Лемма о змее в PlanetMath
• Доказательство леммы о змее в фильме « Моя очередь»