Зигзагообразная лемма

В математике , особенно в гомологической алгебре , лемма о зигзаге утверждает существование определенной длинной точной последовательности в группах гомологии некоторых цепных комплексов . Результат действителен в каждой абелевой категории .

Заявление

В абелевой категории (такой как категория абелевых групп или категория векторных пространств над заданным полем ) пусть $({\mathcal {A}},\partial _{\bullet }),({\mathcal {B}},\partial _{\bullet }')$ и $({\mathcal {C}},\partial _{\bullet }'')$ представляют собой цепные комплексы, которые укладываются в следующую короткую точную последовательность :

$0\longrightarrow {\mathcal {A}}\mathrel {\stackrel {\alpha }{\longrightarrow }} {\mathcal {B}}\mathrel {\stackrel {\beta }{\longrightarrow }} {\mathcal {C}}\longrightarrow 0$

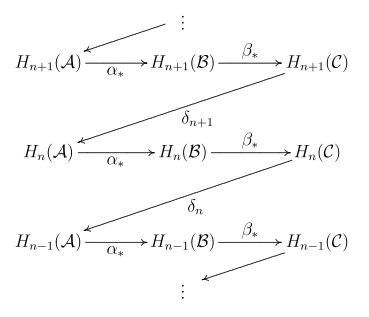
Такая последовательность является сокращением следующей коммутативной диаграммы :

где строки представляют собой точные последовательности , а каждый столбец представляет собой цепной комплекс .

Лемма о зигзаге утверждает, что существует набор граничных карт.

$\delta _{n}:H_{n}({\mathcal {C}})\longrightarrow H_{n-1}({\mathcal {A}}),$

что делает следующую последовательность точной:

Карты $\alpha _{*}^{}$ и $\beta _{*}^{}$ являются обычными отображениями, индуцированными гомологиями. Карты границ $\delta _{n}^{}$ объясняются ниже. Название леммы связано с «зигзагообразным» поведением отображений в последовательности. Вариант версии леммы о зигзаге широко известен как « лемма о змее » (он извлекает суть доказательства леммы о зигзаге, приведенного ниже).

Построение карт границ

Карты $\delta _{n}^{}$ определяются с использованием стандартного аргумента поиска диаграммы. Позволять $c\in C_{n}$ представлять класс в $H_{n}({\mathcal {C}})$, так $\partial _{n}''(c)=0$. Точность строки означает, что $\beta _{n}^{}$ сюръективно, поэтому должно быть какое-то $b\in B_{n}$ с $\beta _{n}^{}(b)=c$. В силу коммутативности диаграммы

$\beta _{n-1}\partial _{n}'(b)=\partial _{n}''\beta _{n}(b)=\partial _{n}''(c)=0.$

По точности,

$\partial _{n}'(b)\in \ker \beta _{n-1}=\mathrm {im} \;\alpha _{n-1}.$

Таким образом, поскольку $\alpha _{n-1}^{}$ инъективен, существует единственный элемент $a\in A_{n-1}$ такой, что $\alpha _{n-1}(a)=\partial _{n}'(b)$. Это цикл, поскольку $\alpha _{n-2}^{}$ является инъективным и

$\alpha _{n-2}\partial _{n-1}(a)=\partial _{n-1}'\alpha _{n-1}(a)=\partial _{n-1}'\partial _{n}'(b)=0,$

с $\partial ^{2}=0$. То есть, $\partial _{n-1}(a)\in \ker \alpha _{n-2}=\{0\}$. Это означает $a$ является циклом, поэтому он представляет класс в $H_{n-1}({\mathcal {A}})$. Теперь мы можем определить

$\delta _{}^{}[c]=[a].$

Определив карты границ, можно показать, что они четко определены (то есть не зависят от выбора c и b ). В доказательстве используются аргументы поиска диаграмм, аналогичные приведенным выше. Такие аргументы также используются, чтобы показать, что последовательность гомологии точна в каждой группе.

См. также

• Последовательность Майера – Виеториса

Ссылки

• Хэтчер, Аллен (2002). Алгебраическая топология . Издательство Кембриджского университета. ISBN  0-521-79540-0 .
• Ланг, Серж (2002), Алгебра , Тексты для аспирантов по математике , том. 211 (пересмотренное третье издание), Нью-Йорк: Springer-Verlag, ISBN.  978-0-387-95385-4 , МР   1878556
• Манкрес, Джеймс Р. (1993). Элементы алгебраической топологии . Нью-Йорк: Вествью Пресс. ISBN  0-201-62728-0 .