Пять лемм

В математике , особенно в гомологической алгебре и других приложениях абелевой теории категорий , лемма о пяти является важной и широко используемой леммой о коммутативных диаграммах .Пятая лемма справедлива не только для абелевых категорий, но и работает в категории групп , например, .

Пять лемм можно рассматривать как комбинацию двух других теорем, четырех лемм , которые двойственны друг другу.

Заявления

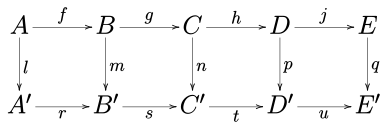
Рассмотрим следующую коммутативную диаграмму в любой абелевой категории (например, категории абелевых групп или категории векторных пространств над заданным полем ) или в категории групп .

Пять лемм утверждают, что если строки точны , m и p — изоморфизмы , l — эпиморфизм и q — мономорфизм , то n также является изоморфизмом.

Две четыре леммы гласят:

1. Если строки коммутативной диаграммы

   

   точны, m и p — эпиморфизмы, а q — мономорфизм, то n — эпиморфизм.
2. Если строки коммутативной диаграммы

   

   точны, m и p — мономорфизмы, а l — эпиморфизм, то n — мономорфизм.

Доказательство

Метод доказательства, который мы будем использовать, обычно называют поиском диаграмм . Мы докажем пять лемм, доказав по отдельности каждую из двух четырех лемм.

Чтобы выполнить поиск диаграммы, мы предполагаем, что мы находимся в категории модулей над некоторым кольцом , так что мы можем говорить об элементах объектов на диаграмме и думать о морфизмах диаграммы как о функциях (фактически гомоморфизмах ), действующих на эти элементы.Тогда морфизм является мономорфизмом тогда и только тогда, когда он инъективен , и является эпиморфизмом тогда и только тогда, когда он сюръективен .Точно так же, чтобы иметь дело с точностью, мы можем думать о ядрах и образах в теоретико-функциональном смысле.Доказательство по-прежнему применимо к любой (малой) абелевой категории из-за теоремы вложения Митчелла , которая утверждает, что любая малая абелева категория может быть представлена ​​как категория модулей над некоторым кольцом.Для категории групп просто преобразуйте все аддитивные обозначения ниже в мультипликативные обозначения и обратите внимание, что коммутативность абелевой группы никогда не используется.

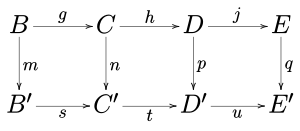
Итак, чтобы доказать (1), предположим, что m и p сюръективны, а q инъективен.

Доказательство (1) в случае, когда $t(c')=0$

Доказательство (1) в случае, когда $t(c')\neq 0$ ненулевое значение

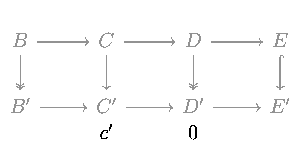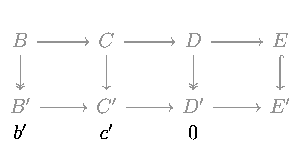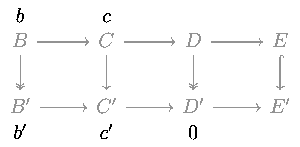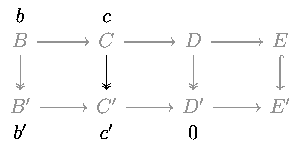
• Пусть c′ будет элементом C′ .
• Поскольку p существует элемент d сюръективен, в D такой, что p ( d ) = t ( c′ ).
• В силу коммутативности диаграммы u ( p ( d )) = q ( j ( d )).
• Поскольку im t = ker u по точности, 0 = u ( t ( c′ )) = u ( p ( d )) = q ( j ( d )).
• Поскольку q инъективен, j ( d ) = 0, поэтому d находится в ker j = im h .
• Следовательно, существует c в C такой, что h ( c ) = d .
• Тогда т ( п ( с )) = п ( час ( с )) = т ( с ' ). Поскольку t — гомоморфизм, отсюда следует, что t ( c′ − n ( c )) = 0.
• По точности c′ − n ( c ) находится в образе s , поэтому существует b′ в B′ такой, что s ( b′ ) = c′ − n ( c ).
• Поскольку m сюръективно, мы можем найти b в B такой, что b′ = m ( b ).
• По коммутативности n ( g ( b )) = s ( m ( b )) = c' - n ( c ).
• Поскольку n является гомоморфизмом, n ( г ( б ) + c ) знак равно n ( г ( б )) + п ( с ) знак равно с ' - п ( с ) + п ( с ) = с ' .
• Следовательно, n сюръективно.

Тогда, чтобы доказать (2), предположим, что m и p инъективны, а l сюръективен.

Доказательство (2)

• Пусть c в C таков, что n ( c ) = 0.
• t ( n ( c )) тогда равно 0.
• По коммутативности p ( h ( c )) = 0.
• Поскольку p инъективен, h ( c ) = 0.
• По точности существует элемент b из B такой, что g ( b ) = c .
• По коммутативности s ( m ( b )) = n ( g ( b )) = n ( c ) = 0.
• По точности тогда существует элемент a′ из A′ такой, что r ( a′ ) = m ( b ).
• Поскольку l сюръективен, существует такой в A , что l ( a ) = a′ .
• По коммутативности m ( f ( a )) = r ( l ( a )) = m ( b ) .
• Поскольку m инъективно, f ( a ) = b .
• Итак, c = g ( f ( a )).
• Поскольку композиция g и f тривиальна, c = 0.
• Следовательно, n инъективно.

Объединение двух четырех лемм теперь доказывает всю пять лемм.

Приложения

Пятая лемма часто применяется к длинным точным последовательностям : при вычислении гомологии или когомологии данного объекта обычно используется более простой подобъект, гомологии/когомологии которого известны, и приходит к длинной точной последовательности, которая включает неизвестные группы гомологий исходного объекта. объект. Одного этого часто недостаточно для определения неизвестных групп гомологии, но если можно сравнить исходный объект и подобъект с хорошо понятными объектами с помощью морфизмов, тогда индуцируется морфизм между соответствующими длинными точными последовательностями, и тогда пять лемм могут быть выполнены. использоваться для определения неизвестных групп гомологии.

См. также

• Короткая лемма о пяти , частный случай леммы о пяти для коротких точных последовательностей.
• Лемма о змее , еще одна лемма, доказанная методом погони за диаграммой.
• Девятая лемма

Ссылки

• Скотт, WR (1987) [1964]. Теория групп . Дувр. ISBN  978-0-486-65377-8 .
• Мэсси, Уильям С. (1991), Базовый курс алгебраической топологии , Тексты для аспирантов по математике, том. 127 (3-е изд.), Springer, ISBN  978-0-387-97430-9