Лагранжева механика

Жозеф-Луи Лагранж (1736–1813)

В физике лагранжева механика — это формулировка классической механики, основанная на принципе стационарного действия (также известном как принцип наименьшего действия). Его представил итало-французский математик и астроном Жозеф-Луи Лагранж в своей презентации Туринской академии наук в 1760 году. кульминацией которого стал его великий опус 1788 года «Аналитическая механика» .

Лагранжева механика описывает механическую систему как пару ( M , L ), состоящую из конфигурационного пространства M и гладкой функции. ${\textstyle L}$ внутри этого пространства, называемого лагранжианом . Для многих систем L = T − V , где T и V — кинетическая и потенциальная энергия системы соответственно.

Принцип стационарного действия требует, чтобы функционал действия системы, полученный из L, оставался в стационарной точке ( максимум , минимум или седло ) на протяжении всей временной эволюции системы. Это ограничение позволяет рассчитывать уравнения движения системы с использованием уравнений Лагранжа.

Введение

Шарик вынужден двигаться по проволоке без трения. Проволока оказывает на бортик силу реакции C, удерживая его на проволоке. Несдерживающей силой N в данном случае является гравитация. Обратите внимание, что исходное положение бусины на проволоке может привести к разным движениям.

Простой маятник. Поскольку стержень жесткий, положение боба ограничивается уравнением f ( x , y ) = 0 , ограничивающая сила C — это натяжение стержня. Опять же, несдерживающая сила N в данном случае — это гравитация.

Предположим, существует бусинка, скользящая по проволоке, или простой качающийся маятник . Если отслеживать каждый из массивных объектов (бусину, маятник) как частицу, расчет движения частицы с использованием механики Ньютона потребует расчета изменяющейся во времени ограничивающей силы, необходимой для удержания частицы в ограниченном движении (сила реакции воздействия проволоки на бусину или натяжения стержня маятника). Для той же задачи с использованием механики Лагранжа смотрят на путь, который может пройти частица, и выбирают удобный набор независимых обобщенных координат , полностью характеризующих возможное движение частицы. Этот выбор исключает необходимость включения ограничивающей силы в результирующую систему уравнений. Уравнений меньше, поскольку напрямую не рассчитывается влияние ограничения на частицу в данный момент.

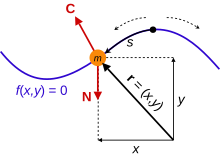
Для широкого спектра физических систем, если размер и форма массивного объекта пренебрежимо малы, полезным упрощением будет считать его точечной частицей . Для системы из N точечных частиц с массами m ₁ , m ₂ , ..., m _N каждая частица имеет вектор положения , обозначаемый r ₁ , r ₂ , ..., r _N . Декартовых координат часто бывает достаточно, поэтому r ₁ = ( x ₁ , y ₁ , z ₁ ) , r ₂ = ( x ₂ , y ₂ , z ₂ ) и так далее. В трехмерном пространстве каждому вектору положения требуются три координаты , чтобы однозначно определить местоположение точки, поэтому существует 3 N координат, которые однозначно определяют конфигурацию системы. Все это определенные точки в пространстве, в которых можно найти частицы; общая точка в пространстве обозначается r = ( x , y , z ) . Скорость каждой частицы показывает , насколько быстро частица движется по своему пути движения, и является производной по времени от ее положения, т.е.

$$\mathbf {v} _{1}={\frac {d\mathbf {r} _{1}}{dt}},\mathbf {v} _{2}={\frac {d\mathbf {r} _{2}}{dt}},\ldots ,\mathbf {v} _{N}={\frac {d\mathbf {r} _{N}}{dt}}$$

В ньютоновской механике уравнения движения задаются законами Ньютона . Второй закон: «Чистая сила равна произведению массы на ускорение ».

$$\sum \mathbf {F} =m{\frac {d^{2}\mathbf {r} }{dt^{2}}}$$

применимо к каждой частице. Для системы N частиц в трех измерениях существует 3 N второго порядка обыкновенных дифференциальных уравнения в положениях частиц, которые необходимо найти.

Лагранжиан

Вместо сил лагранжева механика использует энергии системы. Центральной величиной лагранжевой механики является лагранжиан — функция, которая суммирует динамику всей системы. В целом, лагранжиан имеет единицы энергии, но не имеет единого выражения для всех физических систем. Любую функцию, которая порождает правильные уравнения движения в соответствии с физическими законами, можно принять как лагранжиан. Тем не менее возможно построить общие выражения для больших классов приложений. Нерелятивистский лагранжиан для системы частиц в отсутствие электромагнитного поля имеет вид

$$L=T-V$$

где

$$T={\frac {1}{2}}\sum _{k=1}^{N}m_{k}v_{k}^{2}$$

– полная кинетическая энергия системы, равная сумме Σ кинетических энергий $N$ частицы. Каждая частица помечена $k$ имеет $m_{k}$ и v _к ² = v _k · v _k — квадрат величины его скорости, эквивалентный скалярному произведению скорости на саму себя.

Кинетическая энергия T = T ( v ₁ , v ₂ , ...) является энергией движения системы и является функцией только скоростей v _k , а не положений r _k или времени t , поэтому T = T ( v ₁ , v ₂ , ...) .

V , потенциальная энергия системы, отражает энергию взаимодействия между частицами, т. е. сколько энергии будет иметь одна частица за счет всех остальных, вместе с любыми внешними воздействиями. Для консервативных сил (например, ньютоновской гравитации ) это функция только векторов положения частиц, поэтому V = V ( r ₁ , r ₂ , ...) . Для тех неконсервативных сил, которые можно вывести из соответствующего потенциала (например, электромагнитного потенциала ), также появятся скорости V = V ( r ₁ , r ₂ , ..., v ₁ , v ₂ , ...) . Если существует какое-то внешнее поле или внешняя движущая сила, меняющаяся со временем, потенциал будет меняться со временем, поэтому в большинстве случаев V = V ( r ₁ , r ₂ , ..., v ₁ , v ₂ , ..., t ) .

Как уже отмечалось, такая форма L применима ко многим важным классам систем, но не везде. Для релятивистской лагранжевой механики ее необходимо заменить в целом функцией, согласующейся со специальной или общей теорией относительности. Там, где присутствует магнитное поле, выражение для потенциальной энергии потребуется переформулировать. А для диссипативных сил (например, трения необходимо ввести еще одну функцию ) наряду с L .

Каждая из одной или нескольких частиц может подчиняться одному или нескольким голономным ограничениям ; такое ограничение описывается уравнением вида f ( r , t ) = 0 . Если количество ограничений в системе равно C , то каждое ограничение имеет уравнение: f ₁ ( r , t ) = 0 , f ₂ ( r , t ) = 0 , ..., f _C ( r , t ) = 0 , каждый из которых может применяться к любой из частиц. Если на частицу k наложено ограничение i , то f _i ( r _k , t ) = 0 . В любой момент времени координаты связанной частицы связаны между собой и не являются независимыми. Уравнения ограничений определяют разрешенные пути, по которым могут двигаться частицы, но не определяют, где они находятся или с какой скоростью они движутся в каждый момент времени. Неголономные ограничения зависят от скоростей частиц, ускорений или высших производных положения. Лагранжева механика может быть применена только к системам, ограничения которых, если таковые имеются, являются голономными . Три примера неголономных ограничений: когда уравнения ограничений неинтегрируемы, когда ограничения имеют неравенства или со сложными неконсервативными силами, такими как трение. Неголономные связи требуют специального подхода, и, возможно, придется вернуться к механике Ньютона или использовать другие методы.

Если T или V или оба явно зависят от времени из-за изменяющихся во времени ограничений или внешних влияний, лагранжиан L ( r ₁ , r ₂ , ... v ₁ , v ₂ , ... t ) явно зависит от времени . ни потенциальная, ни кинетическая энергия не зависят от времени, то лагранжиан ( r1 , _{явно не} r2 , _Если ... v1 _L , v2 _, ...) зависит от времени . В любом случае лагранжиан всегда будет иметь неявную зависимость от времени через обобщенные координаты.

С этими определениями уравнения Лагранжа первого рода имеют вид

Уравнения Лагранжа   (первого рода)

${\frac {\partial L}{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {\mathbf {r} }}_{k}}}+\sum _{i=1}^{C}\lambda _{i}{\frac {\partial f_{i}}{\partial \mathbf {r} _{k}}}=0$

где k = 1, 2, ..., N обозначает частицы, существует множитель Лагранжа λ _i для каждого уравнения ограничений f _i , и

$${\frac {\partial }{\partial \mathbf {r} _{k}}}\equiv \left({\frac {\partial }{\partial x_{k}}},{\frac {\partial }{\partial y_{k}}},{\frac {\partial }{\partial z_{k}}}\right)\,,\quad {\frac {\partial }{\partial {\dot {\mathbf {r} }}_{k}}}\equiv \left({\frac {\partial }{\partial {\dot {x}}_{k}}},{\frac {\partial }{\partial {\dot {y}}_{k}}},{\frac {\partial }{\partial {\dot {z}}_{k}}}\right)$$

каждое является сокращением вектора частных производных ∂/∂ по указанным переменным (а не производной по всему вектору). Каждая точка над точкой является сокращением производной по времени . Эта процедура действительно увеличивает количество решаемых уравнений по сравнению с законами Ньютона с 3 N до 3 N + C , поскольку имеется 3 N связанных дифференциальных уравнений второго порядка в координатах положения и множителях, а также C уравнений ограничений. Однако при решении вместе с координатами положения частиц множители могут дать информацию о силах ограничения. Координаты не нужно исключать путем решения уравнений ограничений.

В лагранжиане координаты положения и компоненты скорости являются независимыми переменными , и производные лагранжиана берутся по ним отдельно в соответствии с обычными правилами дифференцирования (например, частная производная L по компоненту z -скорости частицы 2, определяемая как v _{z ,2} = dz ₂ / dt , равна просто ∂ L /∂ v _{z ,2} неуклюжие цепные правила ; не нужно использовать или полные производные, чтобы связать компонент скорости с соответствующей координатой z ₂ ;

В каждом уравнении ограничений одна координата является избыточной, поскольку она определяется на основе других координат. Таким образом, количество независимых координат равно n = 3 N - C . Мы можем преобразовать каждый вектор положения в общий набор из n обобщенных координат , который удобно записать в виде n -кортежа q = ( q ₁ , q ₂ , ... q _n ) , выражая каждый вектор положения и, следовательно, координаты положения: как функции обобщенных координат и времени,

$$\mathbf {r} _{k}=\mathbf {r} _{k}(\mathbf {q} ,t)=(x_{k}(\mathbf {q} ,t),y_{k}(\mathbf {q} ,t),z_{k}(\mathbf {q} ,t),t)\,.$$

Вектор q является точкой конфигурационного пространства системы. Производные по времени от обобщенных координат называются обобщенными скоростями, и для каждой частицы преобразование ее вектора скорости, полной производной ее положения по времени, равно

$${\dot {q}}_{j}={\frac {\mathrm {d} q_{j}}{\mathrm {d} t}}\,,\quad \mathbf {v} _{k}=\sum _{j=1}^{n}{\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}{\dot {q}}_{j}+{\frac {\partial \mathbf {r} _{k}}{\partial t}}\,.$$

Учитывая это v _k , кинетическая энергия в обобщенных координатах зависит от обобщенных скоростей, обобщенных координат и времени, если векторы положения зависят явно от времени из-за изменяющихся во времени ограничений, поэтому ${\textstyle T=T(\mathbf {q} ,{\dot {\mathbf {q} }},t)}$.

При этих определениях уравнения Эйлера–Лагранжа или уравнения Лагранжа второго рода

Уравнения Лагранжа   (второй вид)

${\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {q}}_{j}}}\right)={\frac {\partial L}{\partial q_{j}}}$

— это математические результаты вариационного исчисления , которые также можно использовать в механике. Подстановка в лагранжиан L ( q , d q /d t , t ) дает уравнения движения системы. Количество уравнений уменьшилось по сравнению с механикой Ньютона с 3 N до n = 3 N − C связанных дифференциальных уравнений второго порядка в обобщенных координатах. Эти уравнения вообще не включают в себя ограничивающие силы, необходимо учитывать только силы, не связанные с ограничениями.

Хотя уравнения движения включают частные производные , результаты частных производных по-прежнему представляют собой обыкновенные дифференциальные уравнения в координатах положения частиц. Полная производная по времени, обозначаемая d/d t, часто включает неявное дифференцирование . Оба уравнения являются линейными в лагранжиане, но обычно представляют собой нелинейные связанные уравнения в координатах.

ньютоновской к

Законы Ньютона

Исаак Ньютон (1642-1727)

Для простоты законы Ньютона можно проиллюстрировать для одной частицы без особой потери общности (для системы из N частиц все эти уравнения применимы к каждой частице в системе). Уравнение движения частицы постоянной массы m — это второй закон Ньютона 1687 года в современных векторных обозначениях.

$$\mathbf {F} =m\mathbf {a} \,,$$

где a — его ускорение, а F — результирующая сила, действующая на него. Если масса меняется, уравнение необходимо обобщить, чтобы взять производную по времени от импульса. «В трех пространственных измерениях это система трех связанных обыкновенных дифференциальных уравнений второго порядка , которую необходимо решить, поскольку в этом векторном уравнении есть три компонента. Решением является вектор положения r частицы в момент времени t с учетом начальных условий r , и v когда t = 0 .

Законы Ньютона легко использовать в декартовых координатах, но декартовы координаты не всегда удобны, а для других систем координат уравнения движения могут усложниться. В наборе криволинейных координат ξ = ( ξ ¹ , х ² , х ³ ) , закон в тензорных индексных обозначениях представляет собой «лагранжеву форму»

$$F^{a}=m\left({\frac {\mathrm {d} ^{2}\xi ^{a}}{\mathrm {d} t^{2}}}+\Gamma ^{a}{}_{bc}{\frac {\mathrm {d} \xi ^{b}}{\mathrm {d} t}}{\frac {\mathrm {d} \xi ^{c}}{\mathrm {d} t}}\right)=g^{ak}\left({\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial T}{\partial {\dot {\xi }}^{k}}}-{\frac {\partial T}{\partial \xi ^{k}}}\right)\,,\quad {\dot {\xi }}^{a}\equiv {\frac {\mathrm {d} \xi ^{a}}{\mathrm {d} t}}\,,$$

где F ^а – a -я контравариантная компонента результирующей силы, действующей на частицу, Γ ^а _bc — символы Кристоффеля второго рода,

$$T={\frac {1}{2}}mg_{bc}{\frac {\mathrm {d} \xi ^{b}}{\mathrm {d} t}}{\frac {\mathrm {d} \xi ^{c}}{\mathrm {d} t}}$$

– кинетическая энергия частицы, g _{bc –} ковариантные компоненты метрического тензора криволинейной системы координат. Все индексы a , b , c принимают значения 1, 2, 3. Криволинейные координаты — это не то же самое, что обобщенные координаты.

Представление закона Ньютона в такой форме может показаться чрезмерным усложнением, но у него есть преимущества. Компонентов ускорения в терминах символов Кристоффеля можно избежать, вместо этого оценивая производные кинетической энергии. Если на частицу не действует равнодействующая сила F = 0 , она не ускоряется, а движется с постоянной скоростью по прямой. Математически решения дифференциального уравнения представляют собой геодезические , кривые экстремальной длины между двумя точками пространства (они могут оказаться минимальными, то есть кратчайшими путями, но это не обязательно). В плоском трехмерном реальном пространстве геодезические представляют собой просто прямые линии. Итак, для свободной частицы второй закон Ньютона совпадает с уравнением геодезических и гласит, что свободные частицы следуют геодезическим — экстремальным траекториям, по которым они могут двигаться. Если на частицу действуют силы F ≠ 0 , частица ускоряется за счет действующих на нее сил и отклоняется от геодезических, по которым она следовала бы, если бы была свободна. С соответствующими расширениями приведенных здесь величин из плоского трехмерного пространства в четырехмерное. В искривленном пространстве-времени приведенная выше форма закона Ньютона также переносится и в , Эйнштейна общую теорию относительности и в этом случае свободные частицы следуют геодезическим линиям в искривленном пространстве-времени, которые больше не являются «прямыми линиями» в обычном смысле.

Однако нам все еще необходимо знать общую результирующую силу F, действующую на частицу, что, в свою очередь, требует результирующей несдерживающей силы N плюс результирующей ограничивающей силы C ,

$$\mathbf {F} =\mathbf {C} +\mathbf {N} \,.$$

Силы ограничения могут быть сложными, поскольку они обычно зависят от времени. Кроме того, при наличии ограничений криволинейные координаты не являются независимыми, а связаны одним или несколькими уравнениями ограничений.

Силы ограничений можно либо исключить из уравнений движения, чтобы остались только силы, не связанные с ограничениями, либо включить их путем включения уравнений ограничений в уравнения движения.

Принцип Даламбера

Жан Даламбер (1717–1783)

Одна степень свободы.

Две степени свободы.

Сдерживающая сила C и виртуальное смещение δ r для частицы массы m, удерживаемой кривой. Результирующая несдерживающая сила N. равна

Фундаментальным результатом аналитической механики является принцип Даламбера , введенный в 1708 году Жаком Бернулли для понимания статического равновесия и развитый Даламбером в 1743 году для решения динамических задач. Этот принцип утверждает, что для N частиц виртуальная работа, т. е. работа по виртуальному смещению δ r _k , равна нулю:

$$\sum _{k=1}^{N}(\mathbf {N} _{k}+\mathbf {C} _{k}-m_{k}\mathbf {a} _{k})\cdot \delta \mathbf {r} _{k}=0\,.$$

Виртуальные смещения в δr по определению представляют собой бесконечно малые _k изменения конфигурации системы, согласующиеся с ограничивающими силами, действующими на систему определенный момент времени : т.е. таким образом, что ограничивающие силы поддерживают ограниченное движение. Они не совпадают с реальными смещениями в системе, которые вызваны результирующими связующими и несвязанными силами, действующими на частицу для ускорения и перемещения ее. Виртуальная работа — это работа, совершаемая по виртуальному перемещению для любой силы (связанной или не связанной).

Поскольку для поддержания ограничений силы связи действуют перпендикулярно движению каждой частицы в системе, общая виртуальная работа сил связи, действующих на систему, равна нулю:

$$\sum _{k=1}^{N}\mathbf {C} _{k}\cdot \delta \mathbf {r} _{k}=0\,,$$

так что

$$\sum _{k=1}^{N}(\mathbf {N} _{k}-m_{k}\mathbf {a} _{k})\cdot \delta \mathbf {r} _{k}=0\,.$$

Таким образом, принцип Даламбера позволяет нам сконцентрироваться только на приложенных несвязывающих силах и исключить сдерживающие силы из уравнений движения. Показанная форма также не зависит от выбора координат. Однако его нельзя легко использовать для составления уравнений движения в произвольной системе координат, поскольку смещения δ r _k могут быть связаны уравнением связи, что не позволяет нам приравнять N отдельных слагаемых к 0. Поэтому мы будем искать система взаимно независимых координат, для которой общая сумма будет равна 0 тогда и только тогда, когда отдельные слагаемые равны 0. Установка каждого из слагаемых в 0 в конечном итоге даст нам наши разделенные уравнения движения.

Уравнения движения из принципа Даламбера

имеются ограничения Если на частицу k , то, поскольку координаты положения r _k = ( x _k , y _k , z _k ) связаны между собой уравнением связи, то же самое происходит и с координатами виртуальных смещений δ r _k = ( δx _k , δy _k , δz _k ) . Поскольку обобщенные координаты независимы, мы можем избежать сложностей с δ r _k , перейдя к виртуальным смещениям в обобщенных координатах. Они связаны в той же форме, что и общий дифференциал :

$$\delta \mathbf {r} _{k}=\sum _{j=1}^{n}{\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}\delta q_{j}\,.$$

Частной производной по времени по времени, умноженной на приращение времени, не существует, поскольку это виртуальное смещение, по ограничениям в момент времени .

Первый член в приведенном выше принципе Даламбера представляет собой виртуальную работу, совершаемую несвязывающими силами N _k вдоль виртуальных смещений δ r _k , и может без ограничения общности быть преобразован в обобщенные аналоги по определению обобщенных сил.

$$Q_{j}=\sum _{k=1}^{N}\mathbf {N} _{k}\cdot {\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}\,,$$

так что

$$\sum _{k=1}^{N}\mathbf {N} _{k}\cdot \delta \mathbf {r} _{k}=\sum _{k=1}^{N}\mathbf {N} _{k}\cdot \sum _{j=1}^{n}{\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}\delta q_{j}=\sum _{j=1}^{n}Q_{j}\delta q_{j}\,.$$

Это половина перевода в обобщенные координаты. Осталось преобразовать член ускорения в обобщенные координаты, что не сразу очевидно. Вспоминая лагранжевую форму второго закона Ньютона, можно найти частные производные кинетической энергии по обобщенным координатам и скоростям, дающие желаемый результат:

$$\sum _{k=1}^{N}m_{k}\mathbf {a} _{k}\cdot {\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}={\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial T}{\partial {\dot {q}}_{j}}}-{\frac {\partial T}{\partial q_{j}}}\,.$$

Теперь принцип Даламбера находится в обобщенных координатах, как и требовалось:

$$\sum _{j=1}^{n}\left[Q_{j}-\left({\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial T}{\partial {\dot {q}}_{j}}}-{\frac {\partial T}{\partial q_{j}}}\right)\right]\delta q_{j}=0\,,$$

и поскольку эти виртуальные смещения δq _j независимы и отличны от нуля, коэффициенты можно приравнять нулю, что приводит к уравнениям Лагранжа или обобщенные уравнения движения ,

$$Q_{j}={\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial T}{\partial {\dot {q}}_{j}}}-{\frac {\partial T}{\partial q_{j}}}$$

Эти уравнения эквивалентны законам Ньютона для несвязывающих сил . Обобщенные силы в этом уравнении выводятся только из сил, не являющихся сдерживающими факторами – силы ограничения были исключены из принципа Даламбера, и их не нужно находить. Обобщенные силы могут быть неконсервативными, если они удовлетворяют принципу Даламбера.

Гамильтона

По мере развития системы q прослеживает путь через конфигурационное пространство (показаны только некоторые). Путь, по которому проходит система (красный цвет), имеет стационарное действие (δ S = 0) при небольших изменениях конфигурации системы (δ q ).

Для неконсервативной силы, зависящей от скорости, возможно найти функцию потенциальной энергии V , которая зависит от положения и скорости. Если обобщенные силы Q _i могут быть получены из потенциала V такого, что

$$Q_{j}={\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial V}{\partial {\dot {q}}_{j}}}-{\frac {\partial V}{\partial q_{j}}}\,,$$

приравнивая уравнения Лагранжа и определяя лагранжиан как L = T - V, получаем уравнения Лагранжа второго рода или Эйлера – Лагранжа. уравнения движения

$${\frac {\partial L}{\partial q_{j}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {q}}_{j}}}=0\,.$$

Однако уравнения Эйлера-Лагранжа могут учитывать неконсервативные силы только в том случае, если потенциал можно найти, как показано. Это не всегда возможно для неконсервативных сил, а уравнения Лагранжа не включают в себя какие-либо потенциальные силы, а только обобщенные силы; поэтому они более общие, чем уравнения Эйлера – Лагранжа.

Уравнения Эйлера-Лагранжа также следуют из вариационного исчисления . Вариация равна лагранжиана

$$\delta L=\sum _{j=1}^{n}\left({\frac {\partial L}{\partial q_{j}}}\delta q_{j}+{\frac {\partial L}{\partial {\dot {q}}_{j}}}\delta {\dot {q}}_{j}\right)\,,\quad \delta {\dot {q}}_{j}\equiv \delta {\frac {\mathrm {d} q_{j}}{\mathrm {d} t}}\equiv {\frac {\mathrm {d} (\delta q_{j})}{\mathrm {d} t}}\,,$$

которое имеет вид, аналогичный полному дифференциалу L , но виртуальные перемещения и их производные по времени заменяют дифференциалы, и приращение времени в соответствии с определением виртуальных перемещений отсутствует. Интегрирование по частям по времени может перевести производную по времени от δq _j в ∂ L /∂(d q _j /d t ), в процессе замены d( δq _j )/d t на δq _j , позволяя независимое виртуальные смещения, которые необходимо факторизовать из производных лагранжиана,

$$\int _{t_{1}}^{t_{2}}\delta L\,\mathrm {d} t=\int _{t_{1}}^{t_{2}}\sum _{j=1}^{n}\left({\frac {\partial L}{\partial q_{j}}}\delta q_{j}+{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {q}}_{j}}}\delta q_{j}\right)-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {q}}_{j}}}\delta q_{j}\right)\,\mathrm {d} t\,=\sum _{j=1}^{n}\left[{\frac {\partial L}{\partial {\dot {q}}_{j}}}\delta q_{j}\right]_{t_{1}}^{t_{2}}+\int _{t_{1}}^{t_{2}}\sum _{j=1}^{n}\left({\frac {\partial L}{\partial q_{j}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {q}}_{j}}}\right)\delta q_{j}\,\mathrm {d} t\,.$$

Теперь, если условие δq _j ( t ₁ ) = δq _j ( t ₂ ) = 0 выполняется для всех j , непроинтегрированные члены равны нулю. Если, кроме того, весь интеграл по времени от δL равен нулю, то, поскольку δq _j независимы, и единственный способ сделать определенный интеграл равным нулю - это если подынтегральная функция равна нулю, каждый из коэффициентов δq _j также должен быть равен нулю. Тогда получим уравнения движения. Это можно резюмировать принципом Гамильтона :

$$\int _{t_{1}}^{t_{2}}\delta L\,\mathrm {d} t=0\,.$$

Интеграл по времени от лагранжиана — это еще одна величина, называемая действием , определяемая как

$$S=\int _{t_{1}}^{t_{2}}L\,\mathrm {d} t\,,$$

который является функционалом ; он принимает функцию Лагранжа для всех моментов времени между t ₁ и t ₂ и возвращает скалярное значение. Его размеры такие же, как [ угловой момент ], [энергия]·[время] или [длина]·[импульс]. В соответствии с этим определением принцип Гамильтона таков:

$$\delta S=0\,.$$

Таким образом, вместо того, чтобы думать о частицах, ускоряющихся в ответ на приложенные силы, можно было бы думать о том, что они выбирают путь стационарным действием, при этом конечные точки пути в конфигурационном пространстве остаются фиксированными в начальный и конечный моменты времени. Принцип Гамильтона иногда называют принципом наименьшего действия , однако функционал действия должен быть только стационарным , а не обязательно максимальным или минимальным значением. Любое изменение функционала дает увеличение функционального интеграла действия.

Исторически идея поиска кратчайшего пути, по которому частица может следовать под действием силы, мотивировала первые применения вариационного исчисления к механическим задачам, таким как задача Брахистохроны, решенная Жаном Бернулли в 1696 году, а также Лейбницем , Даниэлем Бернулли , L'Hopital примерно в то же время, а Newton - в следующем году. Сам Ньютон мыслил в духе вариационного исчисления, но не публиковал свои работы. Эти идеи, в свою очередь, приводят к вариационным принципам механики Ферма , Мопертюи , Эйлера , Гамильтона и других.

Принцип Гамильтона можно применить к неголономным связям , если уравнениям связей можно придать определенную форму - линейную комбинацию дифференциалов первого порядка по координатам. Полученное уравнение ограничений можно преобразовать в дифференциальное уравнение первого порядка. Здесь этого не будет.

Множители Лагранжа и ограничения

Лагранжиан L можно варьировать в декартовых r _k координатах для N частиц:

$$\int _{t_{1}}^{t_{2}}\sum _{k=1}^{N}\left({\frac {\partial L}{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {\mathbf {r} }}_{k}}}\right)\cdot \delta \mathbf {r} _{k}\,\mathrm {d} t=0\,.$$

Принцип Гамильтона по-прежнему действует, даже если координаты L не являются независимыми, здесь r _k , но ограничения по-прежнему считаются голономными. Как всегда, конечные точки фиксированы . δ r _k ( t ₁ ) знак равно δ r _k ( t ₂ ) знак равно 0 для всех k . так это просто приравнять коэффициенты при к δrk _δrk нулю, поскольку не являются _{Чего нельзя сделать ,} независимыми. метод множителей Лагранжа Вместо этого для включения ограничений можно использовать . Умножение каждого уравнения ограничения f _i ( r _k , t ) = 0 на множитель Лагранжа λ _i для i = 1, 2, ..., C и добавление результатов к исходному лагранжиану дает новый лагранжиан

$$L'=L(\mathbf {r} _{1},\mathbf {r} _{2},\ldots ,{\dot {\mathbf {r} }}_{1},{\dot {\mathbf {r} }}_{2},\ldots ,t)+\sum _{i=1}^{C}\lambda _{i}(t)f_{i}(\mathbf {r} _{k},t)\,.$$

Множители Лагранжа являются произвольными функциями времени t , но не функциями координат r _k , поэтому множители находятся на равных с координатами положения. Варьирование этого нового лагранжиана и интегрирование по времени дает

$$\int _{t_{1}}^{t_{2}}\delta L'\mathrm {d} t=\int _{t_{1}}^{t_{2}}\sum _{k=1}^{N}\left({\frac {\partial L}{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {\mathbf {r} }}_{k}}}+\sum _{i=1}^{C}\lambda _{i}{\frac {\partial f_{i}}{\partial \mathbf {r} _{k}}}\right)\cdot \delta \mathbf {r} _{k}\,\mathrm {d} t=0\,.$$

Введенные множители можно найти так, чтобы коэффициенты при δ r _k были равны нулю, даже если r _k не являются независимыми. Далее следуют уравнения движения. Из предыдущего анализа получение решения этого интеграла эквивалентно утверждению

$${\frac {\partial L'}{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L'}{\partial {\dot {\mathbf {r} }}_{k}}}=0\quad \Rightarrow \quad {\frac {\partial L}{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {\mathbf {r} }}_{k}}}+\sum _{i=1}^{C}\lambda _{i}{\frac {\partial f_{i}}{\partial \mathbf {r} _{k}}}=0\,,$$

которые являются уравнениями Лагранжа первого рода . Кроме того, уравнения Эйлера-Лагранжа λ _i для нового лагранжиана возвращают уравнения ограничений

$${\frac {\partial L'}{\partial \lambda _{i}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L'}{\partial {\dot {\lambda }}_{i}}}=0\quad \Rightarrow \quad f_{i}(\mathbf {r} _{k},t)=0\,.$$

В случае консервативной силы, заданной градиентом некоторой потенциальной энергии V , функция только координат r _k , замена лагранжиана L = T - V дает

$$\underbrace {{\frac {\partial T}{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial T}{\partial {\dot {\mathbf {r} }}_{k}}}} _{-\mathbf {F} _{k}}+\underbrace {-{\frac {\partial V}{\partial \mathbf {r} _{k}}}} _{\mathbf {N} _{k}}+\sum _{i=1}^{C}\lambda _{i}{\frac {\partial f_{i}}{\partial \mathbf {r} _{k}}}=0\,,$$

и идентифицируя производные кинетической энергии как (отрицательную) результирующую силу и производные потенциала, равные несдерживающей силе, из этого следует, что ограничивающие силы равны

$$\mathbf {C} _{k}=\sum _{i=1}^{C}\lambda _{i}{\frac {\partial f_{i}}{\partial \mathbf {r} _{k}}}\,,$$

тем самым давая силы ограничения явно через уравнения ограничений и множители Лагранжа.

Свойства лагранжиана

Неуникальность

Лагранжиан данной системы не уникален. Лагранжиан L можно умножить на ненулевую константу a и сдвинуть на произвольную константу b , а новый лагранжиан L ′ = aL + b будет описывать то же движение что и L. , Если ограничиться, как указано выше, траекториями q в течение заданного интервала времени [ t _st , t _fin ] } и фиксированными конечными точками P _st = q ( t _st ) и P _fin = q ( t _fin ) , то два лагранжиана, описывающие одну и ту же систему могут отличаться на «полную производную по времени» функции f ( q , t ) :

$$L'(\mathbf {q} ,{\dot {\mathbf {q} }},t)=L(\mathbf {q} ,{\dot {\mathbf {q} }},t)+{\frac {\mathrm {d} f(\mathbf {q} ,t)}{\mathrm {d} t}},$$

где ${\textstyle {\frac {\mathrm {d} f(\mathbf {q} ,t)}{\mathrm {d} t}}}$ означает ${\textstyle {\frac {\partial f(\mathbf {q} ,t)}{\partial t}}+\sum _{i}{\frac {\partial f(\mathbf {q} ,t)}{\partial q_{i}}}{\dot {q}}_{i}.}$

Оба лагранжиана L и L ′ дают одни и те же уравнения движения. поскольку соответствующие действия S и S ′ связаны соотношением

$${\begin{aligned}S'[\mathbf {q} ]&=\int _{t_{\text{st}}}^{t_{\text{fin}}}L'(\mathbf {q} (t),{\dot {\mathbf {q} }}(t),t)\,dt\\[1ex]&=\int _{t_{\text{st}}}^{t_{\text{fin}}}L(\mathbf {q} (t),{\dot {\mathbf {q} }}(t),t)\,dt+\int _{t_{\text{st}}}^{t_{\text{fin}}}{\frac {\mathrm {d} f(\mathbf {q} (t),t)}{\mathrm {d} t}}\,dt\\[1ex]&=S[\mathbf {q} ]+f(P_{\text{fin}},t_{\text{fin}})-f(P_{\text{st}},t_{\text{st}}),\end{aligned}}$$

причем последние два компонента f ( P _fin , t _fin ) и f ( P _st , t _st ) не зависят от q .

Инвариантность относительно точечных преобразований

Учитывая набор обобщенных координат q , если мы заменим эти переменные на новый набор обобщенных координат Q в соответствии с точечным преобразованием Q = Q ( q , t ), которое обратимо как q = q ( Q , t ) , новый лагранжиан L ′ — функция новых координат

$$L'(\mathbf {Q} ,{\dot {\mathbf {Q} }},t)=L(\mathbf {q} (\mathbf {Q} ,t),{\dot {\mathbf {q} }}(\mathbf {Q} ,{\dot {\mathbf {Q} }},t),t)\,,$$

и согласно цепному правилу частного дифференцирования уравнения Лагранжа инвариантны относительно этого преобразования;

$${\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L'}{\partial {\dot {Q}}_{i}}}={\frac {\partial L'}{\partial Q_{i}}}\,.$$

Это может упростить уравнения движения.

Доказательство

Для преобразования координат $Q_{i}=Q_{i}(\mathbf {q} ,t)$, у нас есть

$$d{Q_{i}}=\sum _{k}{\frac {\partial Q_{i}}{\partial q_{k}}}d{q_{k}}+{\frac {\partial Q_{k}}{\partial t}}dt,$$

что подразумевает, что ${\dot {Q_{i}}}=\sum _{k}{\frac {\partial Q_{i}}{\partial q_{k}}}(\mathbf {q} ,t)\,{\dot {q}}_{k}+{\frac {\partial Q_{k}}{\partial t}}(\mathbf {q} ,t)$ что подразумевает, что ${\frac {\partial {\dot {Q_{i}}}}{\partial {\dot {q}}_{k}}}={\frac {\partial Q_{i}}{\partial q_{k}}}$.

Из этого также следует, что:

$${\frac {\partial {\dot {Q_{i}}}}{\partial q_{j}}}=\sum _{k}{\frac {\partial ^{2}Q_{i}}{\partial q_{j}\partial q_{k}}}(\mathbf {q} ,t)\,{\dot {q}}_{k}+{\frac {\partial ^{2}Q_{k}}{\partial q_{j}\partial t}}(\mathbf {q} ,t)$$

и аналогично:

$${\frac {d}{dt}}\left({\frac {\partial {Q_{i}}}{\partial q_{j}}}\right)=\sum _{k}{\frac {\partial ^{2}Q_{i}}{\partial q_{k}\partial q_{j}}}(\mathbf {q} ,t)\,{\dot {q}}_{k}+{\frac {\partial ^{2}Q_{k}}{\partial t\partial q_{j}}}(\mathbf {q} ,t)$$

которые подразумевают, что ${\frac {d}{dt}}\left({\frac {\partial Q_{i}}{\partial q_{k}}}\right)={\frac {\partial {\dot {Q}}_{i}}{\partial q_{k}}}$. Два производных соотношения можно использовать в доказательстве.

Исходя из уравнений Эйлера-Лагранжа в исходном наборе обобщенных координат, имеем:

$${\begin{aligned}{\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {q}}_{i}}}-{\frac {{\partial }L}{\partial q_{i}}}=0\\\sum _{k}\left({\frac {d}{dt}}\left({\frac {\partial L}{\partial {\dot {Q}}_{k}}}{\frac {\partial {\dot {Q}}_{k}}{\partial {\dot {q}}_{i}}}\right)-{\frac {{\partial }L}{\partial Q_{k}}}{\frac {\partial Q_{k}}{\partial {q}_{i}}}-{\frac {{\partial }L}{\partial {\dot {Q}}_{k}}}{\frac {\partial {\dot {Q}}_{k}}{\partial {q}_{i}}}\right)=0\\\sum _{k}\left({\frac {d}{dt}}\left({\frac {\partial L}{\partial {\dot {Q}}_{k}}}\right){\frac {\partial {\dot {Q}}_{k}}{\partial {\dot {q}}_{i}}}+{\frac {\partial L}{\partial {\dot {Q}}_{k}}}{\frac {d}{dt}}\left({\frac {\partial {\dot {Q}}_{k}}{\partial {\dot {q}}_{i}}}\right)-{\frac {{\partial }L}{\partial Q_{k}}}{\frac {\partial {\dot {Q}}_{k}}{\partial {\dot {q}}_{i}}}-{\frac {{\partial }L}{\partial {\dot {Q}}_{k}}}{\frac {d}{dt}}\left({\frac {\partial Q_{k}}{\partial q_{i}}}\right)\right)=0\\\sum _{k}\left({\frac {d}{dt}}\left({\frac {\partial L}{\partial {\dot {Q}}_{k}}}\right)-{\frac {\partial L}{\partial {\dot {Q}}_{k}}}\right){\frac {\partial Q_{k}}{\partial q_{i}}}=0\\\end{aligned}}$$

С момента преобразования из $q\rightarrow Q$ обратима, то отсюда следует, что форма уравнения Эйлера-Лагранжа инвариантна, т. е.

$${\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {Q}}_{i}}}-{\frac {{\partial }L}{\partial Q_{i}}}=0.$$

Циклические координаты

Важным свойством лагранжиана является то, что сохраняющиеся величины из него легко вычислить , . Обобщенный импульс «канонически сопряженный» с координатой q _i, определяется выражением

$$p_{i}={\frac {\partial L}{\partial {\dot {q}}_{i}}}.$$

Если лагранжиан L не что зависит от некоторой координаты q _i , из уравнений Эйлера–Лагранжа немедленно следует,

$${\dot {p}}_{i}={\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {q}}_{i}}}={\frac {\partial L}{\partial q_{i}}}=0$$

и интегрирование показывает, что соответствующий обобщенный импульс равен константе, сохраняющейся величине. Это частный случай теоремы Нётер . Такие координаты называются «циклическими» или «игнорируемыми».

Например, система может иметь лагранжиан

$$L(r,\theta ,{\dot {s}},{\dot {z}},{\dot {r}},{\dot {\theta }},{\dot {\phi }},t)\,,$$

где r и z — длины по прямым линиям, s — длина дуги вдоль некоторой кривой, а θ и φ — углы. Обратите внимание, что z , s и φ отсутствуют в лагранжиане, хотя их скорости отсутствуют. Тогда импульс

$$p_{z}={\frac {\partial L}{\partial {\dot {z}}}}\,,\quad p_{s}={\frac {\partial L}{\partial {\dot {s}}}}\,,\quad p_{\phi }={\frac {\partial L}{\partial {\dot {\phi }}}}\,,$$

все это сохраняющиеся величины. Единицы измерения и характер каждого обобщенного импульса будут зависеть от соответствующей координаты; в этом случае p _z — поступательный момент в направлении z , p _s поступательный момент вдоль кривой s — также измеряется , а p _φ — угловой момент в плоскости, в которой измеряется угол φ . Каким бы сложным ни было движение система такова, что все координаты и скорости будут меняться таким образом, что эти импульсы сохранятся.

Энергия

Учитывая лагранжиан $L,$ гамильтониан есть соответствующей механической системы по определению

$$H={\biggl (}\sum _{i=1}^{n}{\dot {q}}_{i}{\frac {\partial L}{\partial {\dot {q}}_{i}}}{\biggr )}-L.$$

Эта величина будет эквивалентна энергии, если обобщенные координаты являются натуральными координатами, т. е. не имеют явной зависимости от времени при выражении вектора положения: $\mathbf {r} =\mathbf {r} (q_{1},\cdots ,q_{n})$. От:

$$T={\frac {m}{2}}v^{2}={\frac {m}{2}}\sum _{i,j}\left({\frac {\partial {\vec {r}}}{\partial q_{i}}}{\dot {q}}_{i}\right)\cdot \left({\frac {\partial {\vec {r}}}{\partial q_{j}}}{\dot {q}}_{j}\right)={\frac {m}{2}}\sum _{i,j}a_{ij}{\dot {q}}_{i}{\dot {q}}_{j}$$

$$\sum _{k=1}^{n}{\dot {q}}_{k}{\frac {\partial L}{\partial {\dot {q}}_{k}}}=\sum _{k=1}^{n}{\dot {q}}_{k}{\frac {\partial T}{\partial {\dot {q}}_{k}}}={\frac {m}{2}}\left(2\sum _{i,j}a_{ij}{\dot {q}}_{i}{\dot {q}}_{j}\right)=2T$$

$$H=\left(\sum _{i=1}^{n}{\dot {q}}_{i}{\frac {\partial L}{\partial {\dot {q}}_{i}}}\right)-L=2T-(T-V)=T+V=E$$

где $a_{ij}={\frac {\partial \mathbf {r} }{\partial q_{i}}}\cdot {\frac {\partial \mathbf {r} }{\partial q_{j}}}$ — симметричная матрица, определенная для вывода.

Инвариантность при преобразованиях координат

В каждый момент времени t энергия инвариантна относительно конфигурационного пространства изменений координат q → Q , т.е. (с использованием натуральных координат)

$$E(\mathbf {q} ,{\dot {\mathbf {q} }},t)=E(\mathbf {Q} ,{\dot {\mathbf {Q} }},t).$$

Помимо этого результата, приведенное ниже доказательство показывает, что при такой замене координат производные $\partial L/\partial {\dot {q}}_{i}$ изменяются как коэффициенты линейной формы.

Доказательство

Для преобразования координат Q = F ( q ) мы имеем

$$d\mathbf {Q} =F_{*}(\mathbf {q} )d\mathbf {q} ,$$

где $F_{*}(\mathbf {q} )$ - касательная карта векторного пространства

$$\left\{\sum _{i=1}^{n}{\dot {q}}_{i}\cdot \left(\left.{\frac {\partial }{\partial q_{i}}}\right|_{\mathbf {q} }\right)\ {\biggl |}\ {\dot {q}}_{i}\in \mathbb {R} \right\}$$

в векторное пространство

$$\left\{\sum _{i=1}^{n}{\dot {Q}}_{i}\cdot \left(\left.{\frac {\partial }{\partial Q_{i}}}\right|_{F(\mathbf {q} )}\right)\ {\biggl |}\ {\dot {Q}}_{i}\in \mathbb {R} \right\},$$

и

$$\textstyle F_{*}(\mathbf {q} )=\left(\left.{\frac {\partial F_{i}}{\partial q_{j}}}\right|_{\mathbf {q} }\right)_{i,j=1}^{n}$$

является якобианом. В координатах ${\dot {q}}_{i}$ и ${\dot {Q}}_{i},$ предыдущая формула для $d\mathbf {Q}$ имеет форму ${\dot {\mathbf {Q} }}=F_{*}(\mathbf {q} ){\dot {\mathbf {q} }}.$ После дифференциации с использованием правила произведения

$$d{\dot {\mathbf {Q} }}=G(\mathbf {q} ,{\dot {\mathbf {q} }})d\mathbf {q} +F_{*}(\mathbf {q} )d{\dot {\mathbf {q} }},$$

где

$${\begin{aligned}G(\mathbf {q} ,{\dot {\mathbf {q} }})d\mathbf {q} &\,{\stackrel {\text{def}}{=}}\,d(F_{*}(\mathbf {q} )){\dot {\mathbf {q} }}=\left(\sum _{k=1}^{n}{\frac {\partial ^{2}F_{i}}{\partial q_{j}\partial q_{k}}}{\biggl |}_{\mathbf {q} }dq_{k}\right)_{i,j=1}^{n}{\dot {\mathbf {q} }}=\left(\sum _{j=1}^{n}{\dot {q}}_{j}\sum _{k=1}^{n}{\frac {\partial ^{2}F_{i}}{\partial q_{j}\partial q_{k}}}{\biggl |}_{\mathbf {q} }dq_{k}\right)_{i=1,\ldots ,n}^{T}\\&=\left(\sum _{k=1}^{n}dq_{k}\sum _{j=1}^{n}{\frac {\partial ^{2}F_{i}}{\partial q_{j}\partial q_{k}}}{\biggl |}_{\mathbf {q} }{\dot {q}}_{j}\right)_{i=1,\ldots ,n}^{T}=\left(\sum _{j=1}^{n}{\frac {\partial ^{2}F_{i}}{\partial q_{j}\partial q_{k}}}{\biggl |}_{\mathbf {q} }{\dot {q}}_{j}\right)_{i,k=1}^{n}d\mathbf {q} .\end{aligned}}$$

В векторной записи

$${\begin{aligned}dL(\mathbf {Q} ,{\dot {\mathbf {Q} }},t)&={\frac {\partial L}{\partial \mathbf {Q} }}d\mathbf {Q} +{\frac {\partial L}{\partial {\dot {\mathbf {Q} }}}}d{\dot {\mathbf {Q} }}+{\frac {\partial L}{\partial t}}dt\\&=\left({\frac {\partial L}{\partial \mathbf {Q} }}F_{*}(\mathbf {q} )+{\frac {\partial L}{\partial {\dot {\mathbf {Q} }}}}G(\mathbf {q} ,{\dot {\mathbf {q} }})\right)d\mathbf {q} +{\frac {\partial L}{\partial {\dot {\mathbf {Q} }}}}F_{*}(\mathbf {q} )d{\dot {\mathbf {q} }}+{\frac {\partial L}{\partial t}}.\end{aligned}}$$

С другой стороны,

$$dL(\mathbf {q} ,{\dot {\mathbf {q} }},t)={\frac {\partial L}{\partial \mathbf {q} }}d\mathbf {q} +{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}d{\dot {\mathbf {q} }}+{\frac {\partial L}{\partial t}}dt.$$

Ранее упоминалось, что лагранжианы не зависят от выбора координат конфигурационного пространства, т.е. $L(\mathbf {Q} ,{\dot {\mathbf {Q} }},t)=L(\mathbf {q} ,{\dot {\mathbf {q} }},t).$ Одним из следствий этого является то, что $dL(\mathbf {Q} ,{\dot {\mathbf {Q} }},t)=dL(\mathbf {q} ,{\dot {\mathbf {q} }},t),$ и

$${\frac {\partial L}{\partial {\dot {\mathbf {Q} }}}}F_{*}(\mathbf {q} )={\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}.$$

Это свидетельствует о том, что для каждого $\mathbf {q} ,$ ${\dot {\mathbf {q} }},$ и $t,$ $\textstyle \sum \limits _{i=1}^{n}{\frac {\partial L}{\partial {\dot {q}}_{i}}}d{\dot {q}}_{i}$ является корректной линейной формой, коэффициенты которой $\textstyle {\frac {\partial L}{\partial {\dot {q}}_{i}}}$ являются контрвариантными 1-тензорами. Применяя обе части уравнения к ${\dot {\mathbf {q} }}$ и используя приведенную выше формулу для ${\dot {\mathbf {Q} }}$ урожайность

$${\dot {\mathbf {Q} }}{\frac {\partial L}{\partial {\dot {\mathbf {Q} }}}}={\dot {\mathbf {q} }}{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}.$$

Инвариантность энергии $E$ следует.

Сохранение

В лагранжевой механике система замкнута тогда и только тогда, когда ее лагранжиан $L$ явно не зависит от времени. Закон сохранения энергии гласит, что энергия $E$ замкнутой системы является интегралом движения .

Точнее, пусть q = q ( t ) — экстремаль . (Другими словами, q удовлетворяет уравнениям Эйлера–Лагранжа). Взятие полной производной L по времени вдоль этой экстремали и использование уравнений EL приводит к

$${\begin{aligned}{\frac {dL}{dt}}&={\dot {\mathbf {q} }}{\frac {\partial L}{\partial \mathbf {q} }}+{\ddot {\mathbf {q} }}{\frac {\partial L}{\partial \mathbf {\dot {q}} }}+{\frac {\partial L}{\partial t}}\\-{\frac {\partial L}{\partial t}}&={\frac {d}{dt}}\left({\frac {\partial L}{\partial \mathbf {\dot {q}} }}\right){\dot {\mathbf {q} }}+{\ddot {\mathbf {q} }}{\frac {\partial L}{\partial \mathbf {\dot {q}} }}-{\dot {L}}\\-{\frac {\partial L}{\partial t}}&={\frac {d}{dt}}\left({\frac {\partial L}{\partial \mathbf {\dot {q}} }}\mathbf {\dot {q}} -L\right)={\frac {dH}{dt}}\end{aligned}}$$

Если лагранжиан L не зависит явно от времени, то ∂ L /∂ t = 0 , тогда H не меняется с течением времени, эволюция частицы, действительно, является интегралом движения, а это означает, что

$$H(\mathbf {q} (t),{\dot {\mathbf {q} }}(t),t)={\text{constant of time}}.$$

Следовательно, если выбранные координаты были натуральными координатами, энергия сохраняется.

Кинетическая и потенциальная энергии

При всех этих обстоятельствах константа

$$E=T+V$$

– полная энергия системы. Кинетическая и потенциальная энергии по-прежнему изменяются по мере развития системы, но движение системы будет таким, что их сумма, полная энергия, будет постоянной. Это ценное упрощение, поскольку энергия E является константой интегрирования, которая считается произвольной константой для задачи, и может оказаться возможным интегрировать скорости из этого энергетического соотношения для решения координат.

Механическое сходство

Основная статья: Механическое сходство

Если потенциальная энергия является однородной функцией координат и не зависит от времени, и все векторы положения масштабируются с помощью одной и той же ненулевой константы α , r _k ′ = α r _k , так что

$$V(\alpha \mathbf {r} _{1},\alpha \mathbf {r} _{2},\ldots ,\alpha \mathbf {r} _{N})=\alpha ^{N}V(\mathbf {r} _{1},\mathbf {r} _{2},\ldots ,\mathbf {r} _{N})$$

и время масштабируется с коэффициентом β , t ′ = βt , тогда скорости v _k масштабируются с коэффициентом α / β , а кинетическая энергия T – с коэффициентом ( α / β ) ² . Весь лагранжиан масштабируется с помощью одного и того же коэффициента, если

$${\frac {\alpha ^{2}}{\beta ^{2}}}=\alpha ^{N}\quad \Rightarrow \quad \beta =\alpha ^{1-{\frac {N}{2}}}\,.$$

Поскольку длины и времена масштабированы, траектории частиц в системе следуют геометрически схожим путям, различающимся по размеру. Длина l, пройденная за время t по исходной траектории, соответствует новой длине l ′, пройденной за время t ′ по новой траектории, определяемой соотношениями

$${\frac {t'}{t}}=\left({\frac {l'}{l}}\right)^{1-{\frac {N}{2}}}\,.$$

Взаимодействующие частицы

Для данной системы, если две подсистемы A и B не взаимодействуют, лагранжиан L всей системы представляет собой сумму лагранжианов L _A и L _B для подсистем:

$$L=L_{A}+L_{B}\,.$$

Если они взаимодействуют, это невозможно. В некоторых ситуациях можно разделить лагранжиан системы L на сумму невзаимодействующих лагранжианов плюс еще один лагранжиан L _AB, содержащий информацию о взаимодействии:

$$L=L_{A}+L_{B}+L_{AB}\,.$$

Это может быть физически мотивировано тем, что невзаимодействующие лагранжианы представляют собой только кинетические энергии, тогда как лагранжиан взаимодействия представляет собой полную потенциальную энергию системы. Кроме того, в предельном случае незначительного взаимодействия L _AB стремится к нулю, что приводит к описанному выше случаю невзаимодействия.

Распространение на более чем две невзаимодействующие подсистемы является простым: общий лагранжиан представляет собой сумму отдельных лагранжианов для каждой подсистемы. Если есть взаимодействия, то можно добавить лагранжианы взаимодействия.

сингулярных

Из уравнений Эйлера-Лагранжа следует, что:

$${\begin{aligned}{\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {q}}_{i}}}-{\frac {\partial L}{\partial q_{i}}}=0\\{\frac {\partial ^{2}L}{\partial q_{j}\partial {\dot {q}}_{i}}}{\frac {dq_{j}}{dt}}+{\frac {\partial ^{2}L}{\partial {\dot {q}}_{j}\partial {\dot {q}}_{i}}}{\frac {d{\dot {q}}_{j}}{dt}}+{\frac {\partial L}{\partial t}}-{\frac {\partial L}{\partial q_{i}}}=0\\\sum _{j}W_{ij}(q,{\dot {q}},t){\ddot {q}}_{j}={\frac {\partial L}{\partial q_{i}}}-{\frac {\partial L}{\partial t}}-\sum _{j}{\frac {\partial ^{2}L}{\partial {\dot {q}}_{i}\partial q_{j}}}{\dot {q}}_{j}\\\end{aligned}}$$

Где матрица определяется как $W_{ij}={\frac {\partial ^{2}L}{\partial {\dot {q}}_{i}\partial {\dot {q}}_{j}}}$. Если матрица $W$ не является сингулярным, приведенные выше уравнения можно решить, чтобы представить ${\ddot {q}}$ как функция $({\dot {q}},q,t)$. Если матрица необратима, невозможно представить все ${\ddot {q}}$как функция $({\dot {q}},q,t)$ но также гамильтоновы уравнения движения не примут стандартную форму.

Примеры

Следующие примеры применяют уравнения Лагранжа второго рода к механическим задачам.

Консервативная сила

Частица массы m движется под действием консервативной силы, возникающей из градиента ∇ скалярного потенциала ,

$$\mathbf {F} =-{\boldsymbol {\nabla }}V(\mathbf {r} )\,.$$

Если частиц больше, то в соответствии с приведенными выше результатами полная кинетическая энергия представляет собой сумму по всем кинетическим энергиям частиц, а потенциал является функцией всех координат.

Декартовы координаты

Лагранжиан частицы можно записать

$$L(x,y,z,{\dot {x}},{\dot {y}},{\dot {z}})={\frac {1}{2}}m({\dot {x}}^{2}+{\dot {y}}^{2}+{\dot {z}}^{2})-V(x,y,z)\,.$$

Уравнения движения частицы находятся применением уравнения Эйлера–Лагранжа для x координаты

$${\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {x}}}}\right)={\frac {\partial L}{\partial x}}\,,$$

с деривативами

$${\frac {\partial L}{\partial x}}=-{\frac {\partial V}{\partial x}}\,,\quad {\frac {\partial L}{\partial {\dot {x}}}}=m{\dot {x}}\,,\quad {\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {x}}}}\right)=m{\ddot {x}}\,,$$

следовательно

$$m{\ddot {x}}=-{\frac {\partial V}{\partial x}}\,,$$

и аналогично для координат y и z . Собирая уравнения в векторную форму, находим

$$m{\ddot {\mathbf {r} }}=-{\boldsymbol {\nabla }}V$$

что является вторым законом движения Ньютона для частицы, на которую действует консервативная сила.

Полярные координаты в 2D и 3D

Используя сферические координаты ( r , θ , φ ) , обычно используемые в физике (конвенция ISO 80000-2: 2019), где r — радиальное расстояние до начала координат, θ — полярный угол (также известный как широта, зенитный угол, нормальный угол). , или угол наклона), а φ — азимутальный угол, лагранжиан для центрального потенциала равен

$$L={\frac {m}{2}}({\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2}+r^{2}\sin ^{2}\theta \,{\dot {\varphi }}^{2})-V(r)\,.$$

Итак, в сферических координатах уравнения Эйлера–Лагранжа имеют вид

$$m{\ddot {r}}-mr({\dot {\theta }}^{2}+\sin ^{2}\theta \,{\dot {\varphi }}^{2})+{\frac {\partial V}{\partial r}}=0\,,$$

$${\frac {\mathrm {d} }{\mathrm {d} t}}(mr^{2}{\dot {\theta }})-mr^{2}\sin \theta \cos \theta \,{\dot {\varphi }}^{2}=0\,,$$

$${\frac {\mathrm {d} }{\mathrm {d} t}}(mr^{2}\sin ^{2}\theta \,{\dot {\varphi }})=0\,.$$

Координата φ является циклической, поскольку она не входит в лагранжиан, поэтому сохраняющимся импульсом в системе является угловой момент.

$$p_{\varphi }={\frac {\partial L}{\partial {\dot {\varphi }}}}=mr^{2}\sin ^{2}\theta {\dot {\varphi }}\,,$$

в котором r , θ и dφ / dt могут меняться со временем, но только таким образом, чтобы p _φ было постоянным.

Лагранжиан в двумерных полярных координатах восстанавливается путем привязки θ к постоянному значению π /2.

Маятник на подвижной опоре

Эскиз ситуации с определением координат (кликните для увеличения)

Рассмотрим маятник массы m и длины ℓ , прикрепленный к опоре массы M , которая может двигаться вдоль прямой в $x$-направление. Позволять $x$ – координата вдоль линии опоры, а положение маятника обозначим углом $\theta$ от вертикали. Координаты и компоненты скорости качания маятника равны

$${\begin{array}{rll}&x_{\mathrm {pend} }=x+\ell \sin \theta &\quad \Rightarrow \quad {\dot {x}}_{\mathrm {pend} }={\dot {x}}+\ell {\dot {\theta }}\cos \theta \\&y_{\mathrm {pend} }=-\ell \cos \theta &\quad \Rightarrow \quad {\dot {y}}_{\mathrm {pend} }=\ell {\dot {\theta }}\sin \theta \,.\end{array}}$$

Обобщёнными координатами можно считать $x$ и $\theta$. Тогда кинетическая энергия системы равна

$$T={\frac {1}{2}}M{\dot {x}}^{2}+{\frac {1}{2}}m\left({\dot {x}}_{\mathrm {pend} }^{2}+{\dot {y}}_{\mathrm {pend} }^{2}\right)$$

а потенциальная энергия

$$V=mgy_{\mathrm {pend} }$$

давая лагранжиан

$${\begin{array}{rcl}L&=&T-V\\&=&{\frac {1}{2}}M{\dot {x}}^{2}+{\frac {1}{2}}m\left[\left({\dot {x}}+\ell {\dot {\theta }}\cos \theta \right)^{2}+\left(\ell {\dot {\theta }}\sin \theta \right)^{2}\right]+mg\ell \cos \theta \\&=&{\frac {1}{2}}\left(M+m\right){\dot {x}}^{2}+m{\dot {x}}\ell {\dot {\theta }}\cos \theta +{\frac {1}{2}}m\ell ^{2}{\dot {\theta }}^{2}+mg\ell \cos \theta \,.\end{array}}$$

Поскольку x отсутствует в лагранжиане, это циклическая координата. Сохраняющийся импульс равен

$$p_{x}={\frac {\partial L}{\partial {\dot {x}}}}=(M+m){\dot {x}}+m\ell {\dot {\theta }}\cos \theta \,$$

и уравнение Лагранжа для опорной координаты $x$ является

$$(M+m){\ddot {x}}+m\ell {\ddot {\theta }}\cos \theta -m\ell {\dot {\theta }}^{2}\sin \theta =0\,.$$

Уравнение Лагранжа для угла θ имеет вид

$${\frac {\mathrm {d} }{\mathrm {d} t}}\left[m({\dot {x}}\ell \cos \theta +\ell ^{2}{\dot {\theta }})\right]+m\ell ({\dot {x}}{\dot {\theta }}+g)\sin \theta =0;$$

и упрощение

$${\ddot {\theta }}+{\frac {\ddot {x}}{\ell }}\cos \theta +{\frac {g}{\ell }}\sin \theta =0.$$

Эти уравнения могут показаться довольно сложными, но их нахождение с помощью законов Ньютона потребовало бы тщательного определения всех сил, что было бы гораздо более трудоемким и подверженным ошибкам. Рассмотрев предельные случаи, можно проверить правильность этой системы: например, ${\ddot {x}}\to 0$ должно дать уравнения движения простого маятника , покоящегося в некоторой инерциальной системе отсчета , а ${\ddot {\theta }}\to 0$ должно дать уравнения маятника в постоянно ускоряющейся системе и т. д. Более того, при подходящих начальных условиях и выбранном шаге по времени тривиально получить результаты численно, проходя результаты итеративно .

Задача центральной силы двух тел

Основные статьи: Задача двух тел и центральная сила

Два тела массами m ₁ и m ₂ с векторами положения r ₁ и r ₂ находятся на орбите друг друга благодаря притяжению центрального потенциала V . Мы можем записать лагранжиан в терминах координат положения, как они есть, но общепринятой процедурой является преобразование задачи двух тел в задачу одного тела следующим образом. Введем координаты Якоби ; разделение тел р знак равно р ₂ - р ₁ и расположение центра масс R знак равно ( м ₁ р ₁ + м ₂ р ₂ )/( м ₁ + м ₂ ) . Лагранжиан тогда

$$L=\underbrace {{\frac {1}{2}}M{\dot {\mathbf {R} }}^{2}} _{L_{\text{cm}}}+\underbrace {{\frac {1}{2}}\mu {\dot {\mathbf {r} }}^{2}-V(|\mathbf {r} |)} _{L_{\text{rel}}}$$

где М = м ₁ + м ₂ - полная масса, ц ​​= м ₁ м ₂ /( м ₁ + м ₂ ) - приведенная масса , а V - потенциал радиальной силы, который зависит только от величины отрыва | р | = | р ₂ - р ₁ | . Лагранжиан распадается на центра масс член L _cm и относительного движения член L _rel .

Уравнение Эйлера–Лагранжа для R просто

$$M{\ddot {\mathbf {R} }}=0\,,$$

который утверждает, что центр масс движется по прямой с постоянной скоростью.

Поскольку относительное движение зависит только от величины разделения, идеально использовать полярные координаты ( r , θ ) и взять r = | р | ,

$$L_{\text{rel}}={\frac {1}{2}}\mu \left({\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2}\right)-V(r)\,,$$

поэтому θ - циклическая координата с соответствующим сохраняющимся (угловым) моментом.

$$p_{\theta }={\frac {\partial L_{\text{rel}}}{\partial {\dot {\theta }}}}=\mu r^{2}{\dot {\theta }}=\ell \,.$$

Радиальная координата r и угловая скорость d θ /d t могут меняться со временем, но только таким образом, чтобы ℓ была постоянной. Уравнение Лагранжа для r имеет вид

$$\mu r{\dot {\theta }}^{2}-{\frac {dV}{dr}}=\mu {\ddot {r}}\,.$$

Это уравнение идентично радиальному уравнению, полученному с использованием законов Ньютона во вращающейся системе отсчета, то есть системе, вращающейся с уменьшенной массой, поэтому она кажется неподвижной. Исключив угловую скорость d θ /d t из этого радиального уравнения,

$$\mu {\ddot {r}}=-{\frac {\mathrm {d} V}{\mathrm {d} r}}+{\frac {\ell ^{2}}{\mu r^{3}}}\,.$$

которое представляет собой уравнение движения для одномерной задачи, в которой частица массы μ подвергается действию внутренней центральной силы −d V /d r и второй внешней силы, называемой в этом контексте (лагранжевой) центробежной силой (см. центробежная сила#Другие варианты использования термина ):

$$F_{\mathrm {cf} }=\mu r{\dot {\theta }}^{2}={\frac {\ell ^{2}}{\mu r^{3}}}\,.$$

Конечно, если полностью оставаться в рамках одномерной формулировки, ℓ входит только как некий навязанный параметр внешней внешней силы, а его интерпретация как углового момента зависит от более общей двумерной задачи, из которой возникла одномерная проблема. .

Если прийти к этому уравнению, используя механику Ньютона в системе отсчета, вращающейся вместе, интерпретация очевидна как центробежная сила в этой системе отсчета, возникающая из-за вращения самой системы отсчета. Если кто-то приходит к этому уравнению напрямую, используя обобщенные координаты ( r , θ ) и просто следуя лагранжевой формулировке, вообще не задумываясь о системе отсчета, интерпретация такова, что центробежная сила является результатом использования полярных координат . Как говорит Хильдебранд:

«Поскольку такие величины не являются истинными физическими силами, их часто называют силами инерции . Их наличие или отсутствие зависит не от конкретной рассматриваемой проблемы, а от выбранной системы координат ». В частности, если выбраны декартовы координаты, центробежная сила исчезает, и в формулировке участвует только сама центральная сила, которая обеспечивает центростремительную силу для криволинейного движения.

Точку зрения, что фиктивные силы возникают при выборе координат, часто высказывают пользователи метода Лагранжа. Эта точка зрения естественным образом возникает в лагранжевом подходе, поскольку система отсчета (возможно, бессознательно) выбирается путем выбора координат. Например, см. для сравнения лагранжианов в инерциальной и неинерциальной системе отсчета. См. также обсуждение «полных» и «обновленных» лагранжевых формулировок в . К сожалению, такое использование «силы инерции» противоречит ньютоновской идее силы инерции. С точки зрения Ньютона, сила инерции возникает в ускорении системы наблюдения (тот факт, что это не инерциальная система отсчета ), а не в выборе системы координат. Чтобы внести ясность, безопаснее всего называть лагранжевы силы инерции обобщенными силами инерции, чтобы отличать их от ньютоновских векторных сил инерции. То есть не следует следовать Хильдебранду, когда он говорит (стр. 155): «Мы всегда имеем дело с обобщенными силами, скоростями, ускорениями и импульсами. Для краткости прилагательное «обобщенный» будет часто опускаться».

Известно, что лагранжиан системы не единственен. В рамках лагранжева формализма фиктивные силы Ньютона можно идентифицировать по существованию альтернативных лагранжианов, в которых фиктивные силы исчезают, иногда обнаруживаемые путем использования симметрии системы.

неконсервативных

силы

Диссипацию (т.е. неконсервативные системы) также можно рассматривать с помощью эффективного лагранжиана, сформулированного путем определенного удвоения степеней свободы.

В более общей формулировке силы могут быть как консервативными, так и вязкими . подходящее преобразование можно найти из F _i , Рэлей предлагает использовать функцию диссипации D Если следующей формы:

$$D={\frac {1}{2}}\sum _{j=1}^{m}\sum _{k=1}^{m}C_{jk}{\dot {q}}_{j}{\dot {q}}_{k}\,$$

где C _jk — константы, связанные с коэффициентами затухания в физической системе, но не обязательно равные им. Если D определено таким образом, то

$$Q_{j}=-{\frac {\partial V}{\partial q_{j}}}-{\frac {\partial D}{\partial {\dot {q}}_{j}}}$$

и

$${\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {q}}_{j}}}\right)-{\frac {\partial L}{\partial q_{j}}}+{\frac {\partial D}{\partial {\dot {q}}_{j}}}=0\,.$$

Электромагнетизм

Пробная частица — это частица, масса и заряд которой предполагаются настолько малыми, что ее влияние на внешнюю систему незначительно. Часто это гипотетическая упрощенная точечная частица, не имеющая никаких свойств, кроме массы и заряда. Реальные частицы, такие как электроны и ап-кварки, более сложны и имеют дополнительные члены в своих лагранжианах. Поля могут не только образовывать неконсервативные потенциалы, но и эти потенциалы могут зависеть от скорости.

Лагранжиан для заряженной частицы с электрическим зарядом q , взаимодействующей с электромагнитным полем , является типичным примером потенциала, зависящего от скорости. Электрический скалярный потенциал φ = φ ( r , t ) и магнитный векторный потенциал A = A ( r , t ) определяются из электрического поля E = E ( r , t ) и магнитного поля B = B ( r , t ) как следует:

$$\mathbf {E} =-{\boldsymbol {\nabla }}\phi -{\frac {\partial \mathbf {A} }{\partial t}}\,,\quad \mathbf {B} ={\boldsymbol {\nabla }}\times \mathbf {A} \,.$$

Лагранжиан массивной заряженной пробной частицы в электромагнитном поле

$$L={\tfrac {1}{2}}m{\dot {\mathbf {r} }}^{2}+q\,{\dot {\mathbf {r} }}\cdot \mathbf {A} -q\phi \,,$$

называется минимальной связью . Это хороший пример того, когда общее эмпирическое правило , согласно которому лагранжиан равен кинетической энергии минус потенциальная энергия, неверно. В сочетании с уравнением Эйлера-Лагранжа это дает силы Лоренца закон .

$$m{\ddot {\mathbf {r} }}=q\mathbf {E} +q{\dot {\mathbf {r} }}\times \mathbf {B}$$

При калибровочном преобразовании :

$$\mathbf {A} \rightarrow \mathbf {A} +{\boldsymbol {\nabla }}f\,,\quad \phi \rightarrow \phi -{\dot {f}}\,,$$

где f ( r , t ) — любая скалярная функция пространства и времени, вышеупомянутый лагранжиан преобразуется следующим образом:

$$L\rightarrow L+q\left({\dot {\mathbf {r} }}\cdot {\boldsymbol {\nabla }}+{\frac {\partial }{\partial t}}\right)f=L+q{\frac {df}{dt}}\,,$$

который по-прежнему приводит к тому же закону силы Лоренца.

Обратите внимание, что канонический импульс (сопряженный с положением r ) представляет собой кинетический импульс плюс вклад поля A (известный как потенциальный импульс):

$$\mathbf {p} ={\frac {\partial L}{\partial {\dot {\mathbf {r} }}}}=m{\dot {\mathbf {r} }}+q\mathbf {A} \,.$$

Это соотношение также используется в рецепте минимальной связи в квантовой механике и квантовой теории поля . Из этого выражения мы видим, что канонический импульс p не является калибровочно-инвариантным и, следовательно, не является измеримой физической величиной; Однако если r является циклическим (т. е. лагранжиан не зависит от положения r ), что происходит, если поля φ и A однородны, то данный здесь канонический импульс p является сохраняющимся импульсом, а измеримый физический кинетический импульс m v — нет.

и

Идеи лагранжевой механики имеют многочисленные применения в других областях физики и могут использовать обобщенные результаты вариационного исчисления.

классической

Близкой формулировкой классической механики является гамильтонова механика . Гамильтониан определяется формулой

$$H=\sum _{i=1}^{n}{\dot {q}}_{i}{\frac {\partial L}{\partial {\dot {q}}_{i}}}-L\,$$

и может быть получен путем выполнения преобразования Лежандра к лагранжиану, которое вводит новые переменные, канонически сопряженные с исходными переменными. Например, для данного набора обобщенных координат канонически сопряженные переменные представляют собой обобщенные импульсы. Это удваивает количество переменных, но делает дифференциальные уравнения первого порядка. Гамильтониан — особенно распространенная величина в квантовой механике (см. Гамильтониан (квантовая механика) ).

Механика Рутиана представляет собой гибридную формулировку механики Лагранжа и Гамильтона, которая не часто используется на практике, но является эффективной формулировкой для циклических координат.

пространства

Основная статья: Пространство положения и импульса § Лагранжева механика

Уравнения Эйлера – Лагранжа также можно сформулировать в терминах обобщенных импульсов, а не обобщенных координат. Выполнение преобразования Лежандра над обобщенным координатным лагранжианом L ( q , d q /d t , t ) дает обобщенный лагранжиан импульсов L ′( p , d p /d t , t ) в терминах исходного лагранжиана, а также EL уравнения в терминах обобщенных импульсов. Оба лагранжиана содержат одну и ту же информацию, и любой из них можно использовать для определения движения системы. На практике обобщенные координаты удобнее использовать и интерпретировать, чем обобщенные импульсы.

Высшие производные обобщенных координат

Нет никаких математических оснований ограничивать производные обобщенных координат только первым порядком. Можно вывести модифицированные уравнения EL для лагранжиана, содержащего производные более высокого порядка, см. в уравнении Эйлера – Лагранжа подробности . Однако с физической точки зрения существует препятствие для включения производных по времени выше первого порядка, что следует из построения Остроградским канонического формализма для невырожденных лагранжианов с высшими производными, см. Неустойчивость Остроградского.

Оптика

Основная статья: гамильтонова оптика

Лагранжева механика может быть применена к геометрической оптике , применяя вариационные принципы к лучам света в среде, а решение уравнений ЭЛ дает уравнения путей, по которым следуют световые лучи.

формулировка

Основная статья: Релятивистская лагранжева механика

Лагранжева механика может быть сформулирована в специальной теории относительности и общей теории относительности . Некоторые черты лагранжевой механики сохраняются в релятивистских теориях, но быстро возникают трудности в других отношениях. В частности, уравнения ЭЛ принимают ту же форму, и связь между циклическими координатами и сохраняющимися импульсами по-прежнему сохраняется, однако лагранжиан должен быть изменен и не является просто кинетической минус потенциальная энергия частицы. Кроме того, непросто обращаться с многочастичными системами явно ковариантным образом; это может быть возможно, если выделить конкретную систему отсчета.

Квантовая механика

В квантовой механике действие и квантово-механическая фаза связаны через постоянную Планка , а принцип стационарного действия можно понять с точки зрения конструктивной интерференции волновых функций .

В 1948 году Фейнман открыл формулировку интеграла по траекториям, распространяющую принцип наименьшего действия на квантовую механику для электронов и фотонов . В этой формулировке частицы проходят все возможные пути между начальным и конечным состояниями; вероятность конкретного конечного состояния получается суммированием по всем возможным траекториям, ведущим к нему. В классическом режиме формулировка интеграла по траекториям четко воспроизводит принцип Гамильтона и принцип Ферма в оптике .

Классическая теория поля

В лагранжевой механике обобщенные координаты образуют дискретный набор переменных, определяющих конфигурацию системы. В классической теории поля физическая система представляет собой не набор дискретных частиц, а скорее непрерывное поле φ ( r , t ), определенное в области трехмерного пространства. С полем связана лагранжева плотность

$${\mathcal {L}}(\phi ,\nabla \phi ,{\dot {\phi }},\mathbf {r} ,t)$$

определяется через поле и его производные по пространству и времени в точке r и времени t . Аналогично случаю с частицами, для нерелятивистских приложений плотность лагранжа также является плотностью кинетической энергии поля за вычетом плотности его потенциальной энергии (в целом это неверно, и плотность лагранжа должна быть «обратно спроектирована»). Тогда лагранжиан представляет собой объемный интеграл от плотности лагранжа в трехмерном пространстве.

$$L(t)=\int {\mathcal {L}}\,\mathrm {d} ^{3}\mathbf {r}$$

где d ³ r — элемент трехмерного дифференциального объема . Лагранжиан является функцией времени, поскольку плотность лагранжиана имеет неявную пространственную зависимость через поля и может иметь явную пространственную зависимость, но они удаляются в интеграле, оставляя только время в качестве переменной для лагранжиана.

Теорема Нётер

Принцип действия и лагранжев формализм тесно связаны с теоремой Нётер , которая связывает физические сохраняющиеся величины с непрерывными симметриями физической системы.

Если лагранжиан инвариантен относительно симметрии, то полученные уравнения движения также инвариантны относительно этой симметрии. Эта характеристика очень полезна для демонстрации того, что теории согласуются либо со специальной теорией относительности , либо с общей теорией относительности .

См. также

• Канонические координаты
• Основная лемма вариационного исчисления
• Функциональная производная
• Обобщенные координаты
• гамильтонова механика
• Гамильтонова оптика
• Обратная задача лагранжевой механики — общая тема поиска лагранжиана для системы с учетом уравнений движения.
• Лагранжева и эйлерова спецификация поля течения
• точка Лагранжа
• Лагранжева система
• Неавтономная механика
• Проблема Плато
• Ограниченная задача трех тел.

Ссылки

• Лагранж, JL (1811). Аналитическая механика . Полет. 1.
• Лагранж, JL (1815). Аналитическая механика . Полет. 2.
• Пенроуз, Роджер (2007). Дорога к реальности . Винтажные книги. ISBN  978-0-679-77631-4 .
• Ландау, LD ; Лифшиц, Э.М. (15 января 1976 г.). Механика (3-е изд.). Баттерворт Хайнеманн. п. 134. ИСБН  9780750628969 .
• Ландау, Лев ; Лифшиц, Евгений (1975). Классическая теория полей . ООО "Эльзевир" ISBN  978-0-7506-2768-9 .
• Рука, Л.Н.; Финч, доктор юридических наук (1998). Аналитическая механика (2-е изд.). Издательство Кембриджского университета. ISBN  9780521575720 .
• Салетан, Э.Дж.; Хосе, СП (1998). Классическая динамика: современный подход . Издательство Кембриджского университета. ISBN  9780521636360 .
• Киббл, TWB; Беркшир, FH (2004). Классическая механика (5-е изд.). Издательство Имперского колледжа. п. 236. ИСБН  9781860944352 .
• Гольдштейн, Герберт (1980). Классическая механика (2-е изд.). Сан-Франциско, Калифорния: Эддисон Уэсли. ISBN  0201029189 .
• Гольдштейн, Герберт ; Пул, Чарльз П. младший ; Сафко, Джон Л. (2002). Классическая механика (3-е изд.). Сан-Франциско, Калифорния: Эддисон Уэсли. ISBN  0-201-65702-3 .
• Ланцос, Корнелиус (1986). «II §5 Вспомогательные условия: лагранжев λ-метод» . Вариационные принципы механики (Переиздание Университета Торонто, 1970 г., 4-е изд.). Курьер Дувр. п. 43. ИСБН  0-486-65067-7 .
• Феттер, Алабама; Валецка, JD (1980). Теоретическая механика частиц и сплошных сред . Дувр. стр. 53–57. ISBN  978-0-486-43261-8 .
• Принцип наименьшего действия , Р. Фейнман.
• Дворжак Р.; Фрайстеттер, Флориан (2005). «§ 3.2 Уравнения Лагранжа первого рода» . Хаос и стабильность в планетных системах . Биркхойзер. п. 24. ISBN  3-540-28208-4 .
• Хакен, Х (2006). Информация и самоорганизация (3-е изд.). Спрингер. п. 61. ИСБН  3-540-33021-6 .
• Генри Зацкис (1960). «§1.4 Уравнения Лагранжа второго рода» . В Д. Х. Мензеле (ред.). Основные формулы физики . Том. 1 (2-е изд.). Курьер Дувр. п. 160. ИСБН  0-486-60595-7 .
• Хильдебранд, Фрэнсис Бегно (1992). Методы прикладной математики (Перепечатка Прентис-Холла, 1965, 2-е изд.). Курьер Дувр. п. 156. ИСБН  0-486-67002-3 .
• Зак, Михаил; Збилут, Джозеф П.; Мейерс, Рональд Э. (1997). От нестабильности к интеллекту . Спрингер. п. 202. ИСБН  3-540-63055-4 .
• Шабана, Ахмед А. (2008). Вычислительная механика сплошной среды . Издательство Кембриджского университета. стр. 118–119. ISBN  978-0-521-88569-0 .
• Тейлор, Джон Роберт (2005). Классическая механика . Университетские научные книги. п. 297. ИСБН  1-891389-22-Х .
• Падманабхан, Тану (2000). «§2.3.2 Движение во вращающейся системе отсчета» . Теоретическая астрофизика: Астрофизические процессы (3-е изд.). Издательство Кембриджского университета. п. 48. ИСБН  0-521-56632-0 .
• Даути, Ноэль А. (1990). Лагранжево взаимодействие . Addison-Wesley Publishers Ltd. ISBN  0-201-41625-5 .
• Косяков, Б.П. (2007). Введение в классическую теорию частиц и полей . Берлин, Германия: Шпрингер. дои : 10.1007/978-3-540-40934-2 . ISBN  978-3-540-40933-5 .
• Галли, Чад Р. (2013). «Классическая механика неконсервативных систем». Письма о физических отзывах . 110 (17): 174301. arXiv : 1210.2745 . Бибкод : 2013PhRvL.110q4301G . doi : 10.1103/PhysRevLett.110.174301 . ПМИД   23679733 . S2CID   14591873 .
• Бирнхольц, Офек; Хадар, Шахар; Кол, Барак (2014). «Радиационная реакция на уровне действия». Международный журнал современной физики А. 29 (24): 1450132–1450190. arXiv : 1402.2610 . Бибкод : 2014IJMPA..2950132B . дои : 10.1142/S0217751X14501322 . S2CID   118541484 .
• Бирнхольц, Офек; Хадар, Шахар; Кол, Барак (2013). «Теория постньютоновского излучения и реакции». Физический обзор D . 88 (10): 104037. arXiv : 1305.6930 . Бибкод : 2013PhRvD..88j4037B . дои : 10.1103/PhysRevD.88.104037 . S2CID   119170985 .
• Роджер Ф. Ганс (2013). Инженерная динамика: от лагранжиана к моделированию . Нью-Йорк: Спрингер. ISBN  978-1-4614-3929-5 .
• Ганнон, Терри (2006). Самогон за пределами монстра: мост, соединяющий алгебру, модульные формы и физику . Издательство Кембриджского университета. п. 267. ИСБН  0-521-83531-3 .
• Торби, Брюс (1984). «Энергетические методы». Advanced Dynamics для инженеров . Серия HRW в области машиностроения. Соединенные Штаты Америки: Издательство CBS College Publishing. ISBN  0-03-063366-4 .
• Фостер, Дж; Найтингейл, Джей Ди (1995). Краткий курс общей теории относительности (2-е изд.). Спрингер. ISBN  0-03-063366-4 .
• член парламента Хобсон; ГП Эфстатиу; А. Н. Ласенби (2006). Общая теория относительности: введение для физиков . Издательство Кембриджского университета. стр. 79–80. ISBN  9780521829519 .
• Синг, Дж.Л.; Шильд, А. (1949). Тензорное исчисление . первое издание Dover Publications 1978 года. ISBN  978-0-486-63612-2 .
• Кей, Дэвид (апрель 1988 г.). Схема тензорного исчисления Шаума . МакГроу Хилл Профессионал. ISBN  978-0-07-033484-7 .

Дальнейшее чтение

• Гупта, Киран Чандра, Классическая механика частиц и твердых тел (Wiley, 1988).
• Кассель, Кевин (2013). Вариационные методы с применением в науке и технике . Кембридж: Издательство Кембриджского университета. ISBN  978-1-107-02258-4 .
• Гольдштейн , Герберт и др. Классическая механика . 3-е изд., Пирсон, 2002.

Внешние ссылки

• Дэвид Тонг. «Конспекты Кембриджских лекций по классической динамике» . ДАМТП . Проверено 8 июня 2017 г.
• Принцип наименьшего интерактивного действия Отличное интерактивное объяснение/веб-страница
• Жозеф Луи де Лагранж - Полное собрание сочинений (Gallica-Math)
• Вынужденное движение и обобщенные координаты , стр. 4