Фотон

Фотон
Состав	Элементарная частица
Статистика	бозонный
Семья	Калибровочный бозон
Взаимодействия	Электромагнитный , слабый (и гравитационный )
Символ	с
Теоретический	Альберт Эйнштейн (1905) ; Название «фотон» обычно приписывают Гилберту Н. Льюису (1926).
Масса	0 (теоретическое значение) ; < 1 × 10 −18 эВ/ c 2 (экспериментальный предел)
Средний срок службы	Стабильный
Электрический заряд	0 ; < 1 × 10 −35 Это
Цветовой заряд	Нет
Вращаться	1 час
Спиновые состояния	+1 час , −1 час
Паритет	−1
C-паритет	−1
Сжатый	Я ( Дж. ПК   )=0,1(1 −− )

Фотон , (от древнегреческого φῶς , φωτός ( phôs, phōtós ) «свет») — элементарная частица , которая является квантом электромагнитного поля , включая электромагнитное излучение такое как свет и радиоволны , и переносчиком электромагнитной силы . Фотоны — это безмассовые частицы , которые всегда движутся со скоростью света, измеряемой в вакууме. Фотон принадлежит к классу бозонных частиц.

Как и другие элементарные частицы, фотоны лучше всего объясняются квантовой механикой и демонстрируют корпускулярно-волновой дуализм , а их поведение сочетает в себе свойства как волн , так и частиц . ^[2]Современная концепция фотона возникла в течение первых двух десятилетий 20-го века благодаря работе Альберта Эйнштейна , которая основывалась на исследованиях Макса Планка . Когда Планк пытался объяснить, как материя и электромагнитное излучение могут находиться в тепловом равновесии друг с другом, он предположил, что энергию, запасенную внутри материального объекта, следует рассматривать как состоящую из целого числа дискретных частей одинакового размера. Чтобы объяснить фотоэлектрический эффект , Эйнштейн ввел идею о том, что свет сам по себе состоит из дискретных единиц энергии. В 1926 году Гилберт Н. Льюис популяризировал термин «фотон» для обозначения этих энергетических единиц. ^[3]^[4]^[5] Впоследствии многие другие эксперименты подтвердили подход Эйнштейна. ^[6]^[7]^[8]

В Стандартной модели физики элементарных частиц фотоны и другие элементарные частицы описываются как необходимое следствие физических законов, имеющих определенную симметрию в каждой точке пространства-времени . Внутренние свойства частиц, такие как заряд , масса и спин , определяются калибровочной симметрией . Концепция фотона привела к важным достижениям в экспериментальной и теоретической физике, включая лазеры , конденсацию Бозе-Эйнштейна , квантовую теорию поля и вероятностную интерпретацию квантовой механики. Он применялся в фотохимии , микроскопии высокого разрешения и измерении молекулярных расстояний . Более того, фотоны изучались как элементы квантовых компьютеров , а также для применения в оптических изображениях и оптической связи, таких как квантовая криптография .

Номенклатура [ править ]

Слово «кванты» (единственное число «квант», на латыни « сколько» ) использовалось до 1900 года для обозначения частиц или количеств различных величин , включая электричество . В 1900 году немецкий физик Макс Планк изучал излучение черного тела и предположил, что экспериментальные наблюдения, особенно на более коротких волнах , можно было бы объяснить, если бы энергия, запасенная внутри молекулы, была «дискретной величиной, состоящей из целого числа конечных равные части», которые он назвал «энергетическими элементами». ^[9] В 1905 году Альберт Эйнштейн опубликовал статью, в которой предположил, что многие явления, связанные со светом, включая излучение черного тела и фотоэлектрический эффект , можно лучше объяснить, моделируя электромагнитные волны как состоящие из пространственно локализованных дискретных волновых пакетов. ^[10] Он назвал такой волновой пакет квантом света (нем. ein Lichtquant ). ^[а]

Название «фотон» происходит от греческого слова «свет» φῶς (транслитерируется «фос» ). Артур Комптон использовал фотон в 1928 году, имея в виду Гилберта Н. Льюиса , который придумал этот термин в письме в журнал Nature от 18 декабря 1926 года. ^[3]^[11] Это же имя использовалось ранее, но никогда не получало широкого распространения до Льюиса: в 1916 году американский физик и психолог Леонард Т. Троланд , в 1921 году ирландский физик Джон Джоли , в 1924 году французский физиолог Рене Вурмсер (1890–1993), а в 1926 году — французский физик Фритьоф Вольферс (1891–1971). ^[5]Первоначально это название было предложено как единица, связанная с освещением глаза и возникающим в результате ощущением света, а позже использовалось в физиологическом контексте. Хотя теории Вулферса и Льюиса противоречили во многих экспериментах и никогда не были приняты, новое название было принято большинством физиков очень скоро после того, как Комптон использовал его. ^[5]^[б]

В физике фотон обычно обозначают символом $γ$ ( греческая буква гамма ). Этот символ фотона, вероятно, происходит от гамма-лучей , открытых в 1900 году Полем Вилларом . ^[13]^[14] назван Эрнестом Резерфордом было показано, что это форма электромагнитного излучения в 1903 году и в 1914 году Резерфордом и Эдвардом Андраде . ^[15] В химии и оптической технике фотоны обычно обозначаются буквой $hν$ , которая представляет собой энергию фотона , где $h$ — постоянная Планка , а греческая буква $ν$ ( nu фотона ) — частота . ^[16]

Физические свойства [ править ]

Фотон не имеет электрического заряда , ^[17]^[18] обычно считается имеющим нулевую массу покоя ^[19]и является стабильной частицей . Экспериментальный верхний предел массы фотона ^[20]^[21] очень мало, порядка 10 ⁻⁵⁰кг; его время жизни будет больше 10 ¹⁸ годы. ^[22] Для сравнения, возраст Вселенной составляет около 1,38 × 10. ¹⁰ годы.

В вакууме фотон имеет два возможных состояния поляризации . ^[23] Фотон является бозоном электромагнетизма . калибровочным ^[24]^: 29–30 и поэтому все остальные квантовые числа фотона (такие как лептонное число , барионное число и ароматические квантовые числа ) равны нулю. ^[25]Кроме того, фотон подчиняется статистике Бозе-Эйнштейна , а не статистике Ферми-Дирака . То есть они не подчиняются принципу исключения Паули. ^[26]^: 1221 и более чем один может занимать одно и то же связанное квантовое состояние.

Фотоны испускаются во многих природных процессах. Например, когда заряд ускоряется , он испускает синхротронное излучение . Во время молекулярного , атомного или ядерного перехода на более низкий энергетический уровень будут излучаться фотоны различной энергии, начиная от радиоволн и заканчивая гамма-лучами . частицы и соответствующей ей античастицы Фотоны также могут испускаться при аннигиляции электрон (например, -позитронная аннигиляция ). ^[26]^{: 572, 1114, 1172}

энергия импульс Релятивистская и

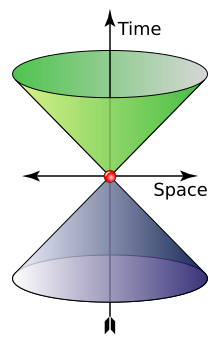
В пустом пространстве фотон движется со скоростью $c$ ( скорость света ), а его энергия и импульс связаны соотношением $E = pc$ , где $p$ — величина вектора импульса $p$ . Это вытекает из следующего релятивистского соотношения с $m = 0$ : ^[27]

E^{2}=p^{2}c^{2}+m^{2}c^{4}~.

Энергия и импульс фотона зависят только от его частоты ( $\nu$ ) или наоборот, его длина волны ( $λ$ ):

E=\hbar \,\omega =h\nu ={\frac {\,h\,c\,}{\lambda }}

{\boldsymbol {p}}=\hbar {\boldsymbol {k}}~,

где $k$ – волновой вектор , где

$к ≡ | к | "=" .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px} 2 π   / λ$ – волновое число , а
$ω \equiv 2 πν$ — угловая частота , а
$ч \equiv h / 2 π$ — приведенная постоянная Планка . ^[28]

С ${\boldsymbol {p}}$ указывает направление распространения фотона, величина его импульса равна

p\equiv \left|{\boldsymbol {p}}\right|=\hbar k={\frac {\,h\nu \,}{c}}={\frac {\,h\,}{\lambda }}~.

Поляризация и момент угловой спиновый

Фотон также несет спиновый угловой момент , который связан с поляризацией фотона . (Лучи света также обладают свойствами, описываемыми как орбитальный угловой момент света ).

Угловой момент фотона имеет два возможных значения: $+ħ$ или $-ħ$ . Эти два возможных значения соответствуют двум возможным чистым состояниям круговой поляризации . Совокупность фотонов в луче света может иметь смесь этих двух значений; линейно поляризованный луч света будет действовать так, как если бы он состоял из равного количества двух возможных угловых моментов. ^[29]^: 325

Спиновый угловой момент света не зависит от его частоты и был экспериментально подтвержден К.В. Раманом и С. Бхагавантамом в 1931 году. ^[30]

Аннигиляция античастиц [ править ]

Столкновение частицы со своей античастицей может создавать фотоны. как минимум два В свободном пространстве должно быть создано фотона, поскольку в центре системы импульсов сталкивающиеся античастицы не имеют чистого импульса, тогда как одиночный фотон всегда имеет импульс (определяемый частотой или длиной волны фотона, который не может быть равен нулю). Следовательно, сохранение импульса (или, что то же самое, трансляционная инвариантность ) требует создания как минимум двух фотонов с нулевым суммарным импульсом. ^[с]^[31]^: 64–65 Энергия двух фотонов или, что то же самое, их частота может быть определена из закона сохранения четырехимпульса .

С другой стороны, фотон можно рассматривать как собственную античастицу (таким образом, «антифотон» — это просто обычный фотон с противоположным импульсом, одинаковой поляризацией и сдвигом по фазе на 180 °). Обратный процесс, образование пар , является доминирующим механизмом, посредством которого фотоны высокой энергии, такие как гамма-лучи, теряют энергию при прохождении через вещество. ^[32] Этот процесс является обратным «аннигиляции одного фотона», допустимой в электрическом поле атомного ядра.

Классические формулы для энергии и импульса электромагнитного излучения могут быть перевыражены через фотонные события. Например, давление электромагнитного излучения на объект возникает в результате передачи импульса фотона в единицу времени и на единицу площади этому объекту, поскольку давление — это сила на единицу площади, а сила — это изменение импульса в единицу времени. ^[33]

массы фотона проверки Экспериментальные

Современные общепринятые физические теории предполагают или предполагают, что фотон строго безмассовый. Если бы фотоны не были полностью безмассовыми, их скорости менялись бы в зависимости от частоты: фотоны с более низкой энергией (более красные) двигались бы немного медленнее, чем фотоны с более высокой энергией. На относительность это не повлияет; так называемая скорость света c тогда была бы не фактической скоростью, с которой движется свет, а константой природы, которая является верхней границей скорости, которую теоретически может достичь любой объект в пространстве-времени. ^[34] Таким образом, это все равно будет скорость ряби пространства-времени ( гравитационных волн и гравитонов ), но не будет скоростью фотонов.

Если бы у фотона была ненулевая масса, были бы и другие эффекты. Закон Кулона будет изменен, и электромагнитное поле получит дополнительную физическую степень свободы . Эти эффекты позволяют получить более чувствительные экспериментальные данные о массе фотона, чем частотная зависимость скорости света. Если закон Кулона не совсем верен, то это допускает существование электрического поля внутри полого проводника, когда он подвергается воздействию внешнего электрического поля. Это обеспечивает возможность точной проверки закона Кулона . ^[35] Нулевой результат такого эксперимента установил предел m ≲ 10. ⁻¹⁴ эВ/ c ². ^[36]

Более четкие верхние пределы массы света были получены в экспериментах, направленных на обнаружение эффектов, вызванных галактическим векторным потенциалом . Хотя галактический векторный потенциал велик, поскольку галактическое магнитное поле существует в больших масштабах длины, только магнитное поле можно было бы наблюдать, если бы фотон был безмассовым. В случае, когда фотон имеет массу, массовый член 1/2 2м ²А _м А ^мповлияет на галактическую плазму. Тот факт, что такие эффекты не наблюдаются, подразумевает верхнюю границу массы фотона m < 3 × 10 ⁻²⁷ эВ/ c ². ^[37] Галактический векторный потенциал также можно исследовать напрямую, измеряя крутящий момент, действующий на намагниченное кольцо. ^[38] Такие методы были использованы для получения более резкого верхнего предела 1,07 × 10 ⁻²⁷ эВ/ c ² (эквивалент 10 ⁻³⁶ дальтоны ), данные Группой данных о частицах . ^[39]

Было показано, что эти резкие ограничения из-за ненаблюдения эффектов, вызванных галактическим векторным потенциалом, зависят от модели. ^[40] Если масса фотона генерируется по механизму Хиггса , то верхний предел m ≲ 10 ⁻¹⁴ эВ/ c ² из проверки закона Кулона.

Историческое развитие [ править ]

В большинстве теорий вплоть до восемнадцатого века свет представлялся состоящим из частиц. Поскольку модели частиц не могут легко объяснить преломление , дифракцию и двойное лучепреломление предложил волновые теории света . света, Рене Декарт (1637 г.) ^[41] Роберт Гук (1665), ^[42] и Христиан Гюйгенс (1678 г.); ^[43] однако модели частиц оставались доминирующими, главным образом благодаря влиянию Исаака Ньютона . ^[44] В начале 19 века Томас Янг и Огюст Френель наглядно продемонстрировали интерференцию и дифракцию света, и к 1850 году волновые модели стали общепринятыми. ^[45] Джеймса Клерка Максвелла 1865 года Предсказание ^[46] что свет был электромагнитной волной, что было подтверждено экспериментально в 1888 году Генрихом Герцем, обнаружившим радиоволны. ^[47] – казалось, это был последний удар по частицам моделей света.

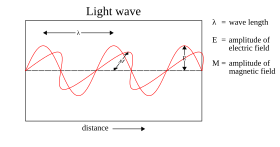
В 1900 году Максвелла теоретическая модель света как колеблющихся электрических и магнитных полей казалась завершенной. Однако некоторые наблюдения не могли быть объяснены какой-либо волновой моделью электромагнитного излучения , что привело к идее, что световая энергия упакована в *кванты,* описываемые $E = hν$ . Более поздние эксперименты показали, что эти кванты света также несут импульс и, таким образом, могут считаться частицами : *фотона , которая привела к более глубокому пониманию самих электрических и магнитных полей.* родилась концепция

не Однако волновая теория Максвелла объясняет всех свойств света. Теория Максвелла предсказывает, что энергия световой волны зависит только от ее интенсивности , а не от частоты ; тем не менее, несколько независимых типов экспериментов показывают, что энергия, сообщаемая светом атомам, зависит только от частоты света, а не от его интенсивности. Например, некоторые химические реакции провоцируются только светом с частотой выше определенного порога; свет частоты ниже порога, независимо от его интенсивности, не инициирует реакцию. Точно так же электроны могут быть выброшены из металлической пластины, если направить на нее свет достаточно высокой частоты ( фотоэлектрический эффект ); энергия выброшенного электрона связана только с частотой света, а не с его интенсивностью. ^[48]^[д]

В то же время исследования излучения черного тела, проводившиеся на протяжении четырех десятилетий (1860–1900 гг.) различными исследователями, ^[50] кульминацией стала Макса Планка гипотеза . ^[51]^[52]что энергия любой системы, которая поглощает или излучает электромагнитное излучение частоты $ν,$ является целым числом, кратным кванту энергии $E$ = $hν$ . Как показал Альберт Эйнштейн , ^[10]^[53] предположить, что некоторая форма квантования энергии необходимо объясняет тепловое равновесие, наблюдаемое между веществом и электромагнитным излучением ; за это объяснение фотоэлектрического эффекта Эйнштейн получил Нобелевскую премию по физике 1921 года. ^[54]

Поскольку теория света Максвелла учитывает все возможные энергии электромагнитного излучения, большинство физиков первоначально предполагали, что квантование энергии является результатом какого-то неизвестного ограничения на материю, которая поглощает или излучает излучение. В 1905 году Эйнштейн первым предположил, что квантование энергии является свойством самого электромагнитного излучения. ^[10] Признавая обоснованность теории Максвелла, Эйнштейн указывал, что многие аномальные эксперименты можно было бы объяснить, если бы энергия максвелловской световой волны была локализована в точечных квантах, которые движутся независимо друг от друга, даже если сама волна непрерывно распространяется по всей поверхности. космос. ^[10] В 1909 году ^[53] и 1916 г., ^[55] Эйнштейн показал, что, если закон Планка принять об излучении черного тела, кванты энергии также должны нести импульс $p = h / λ$ , делая их полноценными частицами. Этот импульс фотона экспериментально наблюдал Артур Комптон . ^[56]за что он получил Нобелевскую премию в 1927 году. Ключевым вопросом тогда было то, как объединить волновую теорию света Максвелла с ее экспериментально наблюдаемой частицей. Ответ на этот вопрос занимал Альберта Эйнштейна всю оставшуюся жизнь. ^[57]и была решена в квантовой электродинамике и ее преемнице, Стандартной модели . (См. § Квантовая теория поля и § Как калибровочный бозон ниже.)

Предсказания Эйнштейна 1905 года были проверены экспериментально несколькими способами в первые два десятилетия 20-го века, как об этом рассказывается в Роберта Милликена . Нобелевской лекции ^[58] Однако до эксперимента Комптона ^[56] показал, что фотоны имеют импульс, пропорциональный их волновому числу (1922 г.), ^{[ нужна полная цитата ]}большинство физиков не хотели верить в то, что электромагнитное излучение само по себе может состоять из частиц. (См., например, Нобелевские лекции в Вене , ^[50] Планк ^[52] и Милликен.) ^[58]Вместо этого было широко распространено мнение, что квантование энергии является результатом какого-то неизвестного ограничения на материю, которая поглощает или излучает излучение. Отношение со временем изменилось. Частично это изменение можно объяснить такими экспериментами, как те, которые выявили комптоновское рассеяние , где было гораздо труднее не приписать квантование самому свету, чтобы объяснить наблюдаемые результаты. ^[59]

Даже после эксперимента Комптона Нильс Бор , Хендрик Крамерс и Джон Слейтер предприняли последнюю попытку сохранить максвелловскую модель непрерывного электромагнитного поля света, так называемую теорию БКС . ^[60]Важной особенностью теории БКС является то, как она трактует сохранение энергии и сохранение импульса . В теории БКС энергия и импульс сохраняются только в среднем при многих взаимодействиях между веществом и излучением. Однако уточненные эксперименты Комптона показали, что законы сохранения справедливы для индивидуальных взаимодействий. ^[61] Соответственно, Бор и его коллеги устроили своей модели «наиболее почетные похороны». ^[57] Тем не менее, неудачи модели БКС вдохновили Вернера Гейзенберга на разработку матричной механики . ^[62]

Некоторые физики упорствовали ^[63]в разработке квазиклассических моделей, в которых электромагнитное излучение не квантуется, а материя подчиняется законам квантовой механики . Хотя к 1970-м годам данные химических и физических экспериментов о существовании фотонов были ошеломляющими, эти доказательства нельзя было считать абсолютно окончательными; поскольку оно основывалось на взаимодействии света с материей, и достаточно полная теория материи в принципе могла бы объяснить эти доказательства. Тем не менее, все полуклассические теории были окончательно опровергнуты в 1970-х и 1980-х годах экспериментами по корреляции фотонов. ^[Это] Таким образом, гипотеза Эйнштейна о том, что квантование является свойством самого света, считается доказанной.

-волновой дуализм и неопределенности Корпускулярно принципы

Фотоны подчиняются законам квантовой механики, поэтому их поведение имеет как волновой, так и корпускулярный аспекты. Когда фотон обнаруживается измерительным прибором, он регистрируется как единая частица. Однако вероятность обнаружения фотона рассчитывается по уравнениям, описывающим волны. Эта комбинация аспектов известна как корпускулярно-волновой дуализм . Например, распределение вероятностей места, в котором может быть обнаружен фотон, четко демонстрирует волновые явления, такие как дифракция и интерференция . Одиночный фотон, проходящий через двойную щель, получает энергию в точке экрана с распределением вероятностей, заданным его интерференционной картиной, определяемой волновыми уравнениями Максвелла . ^[66]Однако эксперименты подтверждают, что фотон — это не короткий импульс электромагнитного излучения; Волны Максвелла фотона будут дифрагировать, но энергия фотона не распространяется по мере распространения, и эта энергия не делится, когда она сталкивается с светоделителем . ^[67] Скорее, полученный фотон действует как точечная частица, поскольку он поглощается или испускается как единое целое сколь угодно малыми системами, включая системы, намного меньшие его длины волны, такие как атомное ядро (≈10 ⁻¹⁵ м в поперечнике) или даже точечный электрон .

Хотя во многих вводных текстах фотоны рассматриваются с использованием математических методов нерелятивистской квантовой механики, это в некотором смысле неуклюжее упрощение, поскольку фотоны по своей природе являются релятивистскими. Поскольку фотоны имеют нулевую массу покоя , никакая волновая функция , определенная для фотона, не может обладать всеми свойствами, знакомыми волновым функциям в нерелятивистской квантовой механике. ^[ф] Чтобы избежать этих трудностей, физики используют описанную ниже теорию вторичного квантования фотонов — квантовую электродинамику , в которой фотоны представляют собой квантованные возбуждения электромагнитных мод. ^[72]

Еще одна трудность — найти правильный аналог принципа неопределенности — идеи, которую часто приписывают Гейзенбергу, который ввел эту концепцию при анализе мысленного эксперимента с участием электрона и фотона высокой энергии . Однако Гейзенберг не дал точных математических определений того, что означает «неопределенность» в этих измерениях. Точная математическая формулировка принципа неопределенности положения-импульса принадлежит Кеннарду , Паули и Вейлю . ^[73]^[74]Принцип неопределенности применяется к ситуациям, когда у экспериментатора есть выбор измерения одной из двух «канонически сопряженных» величин, таких как положение и импульс частицы. Согласно принципу неопределенности, независимо от того, как подготовлена частица, невозможно сделать точный прогноз для обоих альтернативных измерений: если результат измерения положения становится более определенным, результат измерения импульса становится меньше, и наоборот. ^[75] Когерентное состояние минимизирует общую неопределенность, насколько это позволяет квантовая механика. ^[72] Квантовая оптика использует когерентные состояния мод электромагнитного поля. Существует компромисс, напоминающий соотношение неопределенностей положения и импульса, между измерениями амплитуды электромагнитной волны и ее фазы. ^[72] Иногда это неофициально выражается в терминах неопределенности числа фотонов, присутствующих в электромагнитной волне. $\Delta N$ , и неопределенность в фазе волны $\Delta \phi$ . Однако это не может быть соотношением неопределенности типа Кеннарда–Паули–Вейля, поскольку в отличие от положения и импульса фаза $\phi$ не может быть представлено эрмитовым оператором . ^[76]

фотонного газа Модель Бозе- Эйнштейна

В 1924 году Сатьендра Нат Бозе вывел закон Планка об излучении черного тела, не используя какой-либо электромагнетизм, а, скорее, используя модификацию грубого расчета фазового пространства . ^[77] Эйнштейн показал, что эта модификация эквивалентна предположению, что фотоны строго идентичны, и что она подразумевает «таинственное нелокальное взаимодействие». ^[78]^[79]теперь понимается как требование симметричного квантовомеханического состояния . Эта работа привела к концепции когерентных состояний и разработке лазера. В тех же работах Эйнштейн распространил формализм Бозе на материальные частицы (бозоны) и предсказал, что они будут конденсироваться в самое низкое квантовое состояние при достаточно низких температурах; эта конденсация Бозе-Эйнштейна наблюдалась экспериментально в 1995 году. ^[80] использовала его Позже в 1999 году Лене Хау для замедления, а затем полной остановки света. ^[81] и 2001. ^[82]

Современный взгляд на это состоит в том, что фотоны в силу своего целочисленного спина являются бозонами (в отличие от фермионов с полуцелым спином). По теореме о спиновой статистике все бозоны подчиняются статистике Бозе – Эйнштейна (тогда как все фермионы подчиняются статистике Ферми – Дирака ). ^[83]

Стимулированное и спонтанное излучение [ править ]

Вынужденное излучение (при котором фотоны «клонируют» себя) было предсказано Эйнштейном в его кинетическом анализе и привело к разработке лазера . Выводы Эйнштейна вдохновили на дальнейшее развитие квантовой трактовки света, что привело к статистической интерпретации квантовой механики.

В 1916 году Альберт Эйнштейн показал, что закон излучения Планка может быть выведен на основе полуклассического статистического подхода к фотонам и атомам, который предполагает наличие связи между скоростью, с которой атомы излучают и поглощают фотоны. Условие следует из предположения, что функции испускания и поглощения излучения атомами независимы друг от друга и что тепловое равновесие устанавливается за счет взаимодействия излучения с атомами. Предположим, что полость находится в тепловом равновесии со всеми своими частями и заполнена электромагнитным излучением , а атомы могут излучать и поглощать это излучение. Тепловое равновесие требует, чтобы плотность энергии $\rho (\nu )$ фотонов с частотой $\nu$ (которая пропорциональна их плотности числа ) в среднем постоянна во времени; следовательно, скорость испускания фотонов любой конкретной частоты должна равняться скорости их поглощения . ^[84]

Эйнштейн начал с постулирования простых соотношений пропорциональности для различных скоростей реакций. В его модели скорость $R_{ji}$ для системы, поглощающей фотон частоты $\nu$ и переход от более низкой энергии $E_{j}$ к более высокой энергии $E_{i}$ пропорциональна числу $N_{j}$ атомов с энергией $E_{j}$ и плотности энергии $\rho (\nu )$ окружающих фотонов этой частоты,

R_{ji}=N_{j}B_{ji}\rho (\nu )\!

где $B_{ji}$ – константа скорости поглощения. Для обратного процесса возможны две возможности: спонтанное испускание фотона или испускание фотона, инициированное взаимодействием атома с пролетающим фотоном и возвратом атома в состояние с более низкой энергией. Согласно подходу Эйнштейна, соответствующая скорость $R_{ij}$ для излучения фотонов частоты $\nu$ и переход от более высокой энергии $E_{i}$ к более низкой энергии $E_{j}$ является

R_{ij}=N_{i}A_{ij}+N_{i}B_{ij}\rho (\nu )\!

где $A_{ij}$ — константа скорости спонтанного испускания фотона , и $B_{ij}$ — константа скорости выбросов в ответ на фотоны окружающей среды ( индуцированное или стимулированное излучение ). В термодинамическом равновесии число атомов в состоянии $i$ и те, кто в штате $j$ в среднем должен быть постоянным; следовательно, ставки $R_{ji}$ и $R_{ij}$ должно быть равным. Кроме того, по аргументам, аналогичным выводу статистики Больцмана , отношение $N_{i}$ и $N_{j}$ является $g_{i}/g_{j}\exp {(E_{j}-E_{i})/(kT)},$ где $g_{i}$ и $g_{j}$ это вырождение государства $i$ и что из $j$ , соответственно, $E_{i}$ и $E_{j}$ их энергии, $k$ Больцмана постоянная и $T$ системы температура . Отсюда легко вывести, что

$g_{i}B_{ij}=g_{j}B_{ji}$ и

A_{ij}={\frac {8\pi h\nu ^{3}}{c^{3}}}B_{ij}.

The $A_{ij}$ и $B_{ij}$ все вместе известны как коэффициенты Эйнштейна . ^[85]

Эйнштейн не смог полностью обосновать свои уравнения скорости, но утверждал, что должна быть возможность вычислить коэффициенты $A_{ij}$ , $B_{ji}$ и $B_{ij}$ как только физики получили «механику и электродинамику, модифицированную с учетом квантовой гипотезы». ^[86] Вскоре после этого, в 1926 году, Поль Дирак вывел $B_{ij}$ константы скорости с использованием полуклассического подхода, ^[87] а в 1927 году ему удалось вывести все константы скорости из первых принципов в рамках квантовой теории. ^[88]^[89]Работа Дирака легла в основу квантовой электродинамики, т. е. квантования самого электромагнитного поля. Подход Дирака также называют вторым квантованием или квантовой теорией поля ; ^[90]^[91]^[92] более ранние квантово-механические подходы рассматривали материальные частицы только как квантово-механические, а не как электромагнитное поле.

Эйнштейна беспокоило то, что его теория казалась неполной, поскольку она не определяла направление спонтанно испускаемого фотона. Вероятностная природа движения световых частиц была впервые рассмотрена Ньютоном при рассмотрении двойного лучепреломления и, в более общем плане, расщепления световых лучей на границах раздела на прошедший и отраженный луч. Ньютон предположил, что скрытые переменные в легкой частице определяют, какой из двух путей выберет одиночный фотон. ^[44] Точно так же Эйнштейн надеялся на более полную теорию, которая не оставляла бы ничего на волю случая, начиная свое разделение. ^[57]из квантовой механики. По иронии судьбы, Борна Макса вероятностная интерпретация волновой функции ^[93]^[94] был вдохновлен более поздними работами Эйнштейна по поиску более полной теории. ^[95]

Квантовая теория поля [ править ]

Квантование электромагнитного поля [ править ]

Различные *электромагнитные моды* (например, изображенные здесь) можно рассматривать как независимые простые гармонические генераторы . Фотон соответствует единице энергии E = hν в его электромагнитной моде.

В 1910 году Питер Дебай вывел закон излучения черного тела Планка на основе относительно простого предположения. ^[96] Он разложил электромагнитное поле в полости на его моды Фурье и предположил, что энергия в любой моде является целым кратным $h\nu$ , где $\nu$ – частота электромагнитной моды. Закон Планка об излучении черного тела сразу же следует как геометрическая сумма. Однако подход Дебая не смог дать правильную формулу для колебаний энергии излучения черного тела, которую вывел Эйнштейн в 1909 году. ^[53]

В 1925 году Борн , Гейзенберг и Джордан ключевым образом переосмыслили концепцию Дебая. ^[97]Как можно показать классически, моды Фурье электромагнитного поля — полный набор плоских электромагнитных волн, индексированных их волновым вектором k и состоянием поляризации — эквивалентны набору несвязанных простых гармонических осцилляторов . Известно, что с квантовомеханической точки зрения энергетические уровни таких осцилляторов $E=nh\nu$ , где $\nu$ — частота генератора. Ключевым новым шагом было определение электромагнитной моды с энергией $E=nh\nu$ как государство с $n$ фотоны, каждый из энергии $h\nu$ . Этот подход дает правильную формулу колебаний энергии.

Диаграмма Фейнмана двух электронов, взаимодействующих путем обмена виртуальным фотоном.

Дирак пошел еще дальше. ^[88]^[89]Он рассматривал взаимодействие между зарядом и электромагнитным полем как небольшое возмущение, которое вызывает переходы в фотонных состояниях, изменяя количество фотонов в модах, сохраняя при этом в целом энергию и импульс. Дирак смог вывести теорию Эйнштейна. $A_{ij}$ и $B_{ij}$ коэффициенты из первых принципов и показал, что статистика фотонов Бозе-Эйнштейна является естественным следствием правильного квантования электромагнитного поля (рассуждения Бозе шли в противоположном направлении; он вывел закон Планка об излучении черного тела, предположив статистику B-E) . Во времена Дирака еще не было известно, что все бозоны, включая фотоны, должны подчиняться статистике Бозе-Эйнштейна.

Дирака второго порядка Теория возмущений может включать виртуальные фотоны , переходные промежуточные состояния электромагнитного поля; статические электрические и магнитные взаимодействия опосредуются такими виртуальными фотонами. В таких квантовых теориях поля наблюдаемых амплитуда вероятности событий вычисляется путем суммирования по всем возможным промежуточным шагам, даже по тем, которые нефизичны; следовательно, виртуальные фотоны не обязаны удовлетворять $E=pc$ , и может иметь дополнительные поляризации состояния ; В зависимости от используемого датчика виртуальные фотоны могут иметь три или четыре состояния поляризации вместо двух состояний реальных фотонов. Хотя эти временные виртуальные фотоны невозможно наблюдать, они вносят ощутимый вклад в вероятность наблюдаемых событий. ^[98]

Действительно, такие вычисления возмущений второго и более высокого порядка могут давать, по-видимому, бесконечный вклад в сумму. Такие нефизические результаты корректируются методом перенормировки . ^[99]

Другие виртуальные частицы также могут способствовать суммированию; например, два фотона могут взаимодействовать косвенно через виртуальные электрон - позитрон пары . ^[100] Такое фотон-фотонное рассеяние (см. двухфотонную физику ), а также электрон-фотонное рассеяние должно стать одним из режимов работы планируемого ускорителя частиц — Международного линейного коллайдера . ^[101]

В современной физики обозначениях квантовое состояние электромагнитного поля записывается как состояние Фока — тензорное произведение состояний для каждой электромагнитной моды.

|n_{k_{0}}\rangle \otimes |n_{k_{1}}\rangle \otimes \dots \otimes |n_{k_{n}}\rangle \dots

где $|n_{k_{i}}\rangle$ представляет состояние, в котором $\,n_{k_{i}}$ фотоны находятся в режиме $k_{i}$ . В этих обозначениях рождение нового фотона в режиме $k_{i}$ (например, испускаемый при атомном переходе) записывается как $|n_{k_{i}}\rangle \rightarrow |n_{k_{i}}+1\rangle$ . Эти обозначения просто выражают описанную выше концепцию Борна, Гейзенберга и Джордана и не добавляют никакой физики.

Как калибровочный бозон [ править ]

Электромагнитное поле можно понимать как калибровочное поле , то есть как поле, возникающее в результате требования, чтобы калибровочная симметрия сохранялась независимо в каждой позиции пространства-времени . ^[102] Для электромагнитного поля эта калибровочная симметрия представляет собой абелеву U(1)-симметрию комплексных чисел с абсолютным значением 1, которая отражает способность изменять фазу комплексного поля, не затрагивая наблюдаемые или действительнозначные функции , сделанные из него, такие как энергия или лагранжиан .

Кванты абелева калибровочного поля должны быть безмассовыми незаряженными бозонами, пока симметрия не нарушена; следовательно, предсказано, что фотон не имеет массы, имеет нулевой электрический заряд и целочисленный спин. Особая форма электромагнитного взаимодействия определяет, что фотон должен иметь спин ±1; таким образом, его спиральность должна быть $\pm \hbar$ . Эти две спиновые компоненты соответствуют классическим представлениям о правостороннем и левостороннем циркулярно поляризованном свете. Однако переходные виртуальные фотоны квантовой электродинамики могут также принимать нефизические состояния поляризации. ^[102]

В преобладающей Стандартной модели физики фотон является одним из четырех калибровочных бозонов в электрослабом взаимодействии ; остальные три обозначаются W ⁺, В ⁻ и З ⁰и ответственны за слабое взаимодействие . В отличие от фотона, эти калибровочные бозоны имеют массу благодаря механизму , который нарушает их калибровочную симметрию SU(2) . Объединение фотона с W- и Z-калибровочными бозонами в электрослабом взаимодействии было осуществлено Шелдоном Глэшоу , Абдусом Саламом и Стивеном Вайнбергом , за что они были удостоены Нобелевской премии по физике 1979 года. ^[103]^[104]^[105]Физики продолжают выдвигать гипотезы о теориях великого объединения , которые связывают эти четыре калибровочных бозона с восемью глюонными калибровочными бозонами квантовой хромодинамики ; однако ключевые предсказания этих теорий, такие как распад протона , не наблюдались экспериментально. ^[106]

Адронные свойства [ править ]

Измерения взаимодействия между энергичными фотонами и адронами показывают, что взаимодействие гораздо более интенсивное, чем ожидалось при взаимодействии простых фотонов с электрическим зарядом адрона. Более того, взаимодействие энергичных фотонов с протонами аналогично взаимодействию фотонов с нейтронами. ^[107]несмотря на то, что структуры электрического заряда протонов и нейтронов существенно различаются. теория под названием «Доминирование векторных мезонов» Для объяснения этого эффекта была разработана (VMD). Согласно ВМД, фотон представляет собой суперпозицию чистого электромагнитного фотона, который взаимодействует только с электрическими зарядами и векторными мезонами. ^[108] Однако при экспериментальном исследовании на очень коротких расстояниях внутренняя структура фотона распознается как поток кварковых и глюонных компонент, квазисвободный согласно асимптотической свободе в КХД и описываемый структурной функцией фотона . ^[109]^[110] Всестороннее сравнение данных с теоретическими предсказаниями было представлено в обзоре 2000 года. ^[111]

Вклад в массу системы [ править ]

Энергия системы, испускающей фотон, уменьшается на энергию $E$ фотона, измеренного в остальной системе отсчета излучающей системы, что может привести к уменьшению массы на величину ${E}/{c^{2}}$ . Аналогично, масса системы, поглощающей фотон, увеличивается на соответствующую величину. В качестве приложения энергетический баланс ядерных реакций с участием фотонов обычно записывается через массы участвующих ядер и в виде ${E}/{c^{2}}$ для гамма-фотонов (и для других соответствующих энергий, таких как энергия отдачи ядер). ^[112]

Эта концепция применяется в ключевых предсказаниях квантовой электродинамики (КЭД, см. выше). В этой теории масса электронов (или, в более общем плане, лептонов) модифицируется путем включения вклада в массу виртуальных фотонов с помощью метода, известного как перенормировка . Такие « радиационные поправки » способствуют ряду предсказаний КЭД, таких как магнитный дипольный момент лептонов сверхтонкая , лэмбовский сдвиг и структура связанных лептонных пар, таких как мюоний и позитроний . ^[113]

Поскольку фотоны вносят вклад в тензор энергии-импульса , они оказывают гравитационное притяжение на другие объекты, согласно общей теории относительности . И наоборот, фотоны сами подвергаются воздействию гравитации; их обычно прямые траектории могут быть искривлены искривленным пространством-временем , как в случае гравитационного линзирования , а их частоты могут быть снижены за счет перехода к более высокому гравитационному потенциалу , как в эксперименте Паунда-Ребки . Однако эти эффекты не характерны для фотонов; точно такие же эффекты были бы предсказаны для классических электромагнитных волн . ^[114]

В деле [ править ]

Свет, который проходит через прозрачную материю, делает это с меньшей скоростью, чем c — скорость света в вакууме. Коэффициент, на который уменьшается скорость, называется показателем преломления материала. В классической волновой картине замедление можно объяснить тем, что свет вызывает электрическую поляризацию в веществе, поляризованное вещество излучает новый свет, и этот новый свет интерферирует с исходной световой волной, образуя задержанную волну. В картине частиц замедление вместо этого можно описать как смешивание фотона с квантовыми возбуждениями материи с образованием квазичастиц, известных как поляритон ( см. в этом списке некоторые другие квазичастицы ); этот поляритон имеет ненулевую эффективную массу , что означает, что он не может двигаться со скоростью c . Свет разных частот может проходить сквозь материю с разной скоростью ; это называется дисперсией (не путать с рассеянием). В некоторых случаях это может привести к чрезвычайно низкой скорости света в материи. Эффекты взаимодействия фотонов с другими квазичастицами можно наблюдать непосредственно в Комбинационное рассеяние и рассеяние Бриллюэна . ^[115]

Фотоны могут рассеиваться веществом. Например, фотоны на пути от ядра Солнца вступают в такое количество столкновений , что лучистой энергии может потребоваться около миллиона лет, чтобы достичь поверхности; ^[116] однако, оказавшись в открытом космосе, фотону требуется всего 8,3 минуты, чтобы достичь Земли. ^[117]

Фотоны также могут поглощаться ядрами, атомами или молекулами, вызывая переходы между их энергетическими уровнями . Классическим примером является молекулярный переход сетчатки (C ₂₀ H ₂₈ O), который отвечает за зрение , лауреатом Нобелевской премии , открытый в 1958 году биохимиком Джорджем Уолдом и его сотрудниками. Поглощение вызывает цис-транс- изомеризацию , которая в сочетании с другими подобными переходами преобразуется в нервные импульсы. Поглощение фотонов может даже разорвать химические связи, как фотодиссоциации хлора ; при это предмет фотохимии . ^[118]^[119]

Технологические приложения

Фотоны имеют множество применений в технике. Эти примеры выбраны для иллюстрации применения фотонов как таковых , а не обычных оптических устройств, таких как линзы и т. д., которые могли бы работать в рамках классической теории света. Лазер является важным применением и обсуждается выше в разделе стимулированного излучения .

Отдельные фотоны можно обнаружить несколькими методами. Классический фотоумножитель использует фотоэлектрический эффект : фотон достаточной энергии ударяется о металлическую пластину и выбивает электрон, вызывая постоянно усиливающуюся лавину электронов. Полупроводниковые чипы устройств с зарядовой связью используют аналогичный эффект: падающий фотон генерирует заряд на микроскопическом конденсаторе , который можно обнаружить. Другие детекторы, такие как счетчики Гейгера, используют способность фотонов ионизировать молекулы газа, содержащиеся в устройстве, вызывая заметное изменение проводимости газа. ^[120]

Формула энергии Планка $E=h\nu$ часто используется инженерами и химиками при проектировании как для расчета изменения энергии в результате поглощения фотона, так и для определения частоты света, излучаемого в результате испускания данного фотона. Например, спектр излучения газоразрядной лампы можно изменить, наполнив ее газами (смесями) с различной конфигурацией электронных энергетических уровней . ^[121]

При некоторых условиях энергетический переход может быть возбужден «двумя» фотонами, чего по отдельности будет недостаточно. Это позволяет использовать микроскопию с более высоким разрешением, поскольку образец поглощает энергию только в том спектре, где два луча разного цвета значительно перекрываются, что можно сделать намного меньшим, чем объем возбуждения одного луча (см. Микроскопия с двухфотонным возбуждением ). Более того, эти фотоны наносят меньший вред образцу, поскольку имеют меньшую энергию. ^[122]

В некоторых случаях два энергетических перехода могут быть связаны так, что, когда одна система поглощает фотон, другая соседняя система «крадет» его энергию и повторно излучает фотон другой частоты. Это основа резонансного переноса энергии флуоресценции — метода, который используется в молекулярной биологии для изучения взаимодействия подходящих белков . ^[123]

Несколько различных типов аппаратных генераторов случайных чисел предусматривают обнаружение одиночных фотонов. В одном примере для каждого бита случайной последовательности, которая должна быть создана, фотон отправляется в светоделитель . В такой ситуации возможны два равновероятных исхода. Фактический результат используется для определения того, является ли следующий бит в последовательности «0» или «1». ^[124]^[125]

Квантовая оптика и вычисления [ править ]

Много исследований посвящено применению фотонов в области квантовой оптики . Фотоны, похоже, хорошо подходят в качестве элементов чрезвычайно быстрого квантового компьютера , а квантовая запутанность фотонов находится в центре внимания исследований. Нелинейные оптические процессы — еще одна активная область исследований, в которой рассматриваются такие темы, как двухфотонное поглощение , автофазовая модуляция , модуляционная нестабильность и оптические параметрические генераторы . Однако такие процессы обычно не требуют предположения о фотонах как таковых ; их часто можно моделировать, рассматривая атомы как нелинейные осцилляторы. Нелинейный процесс спонтанного параметрического преобразования с понижением частоты часто используется для создания однофотонных состояний. Наконец, фотоны необходимы в некоторых аспектах оптической связи , особенно в квантовой криптографии . ^[126]

Двухфотонная физика изучает взаимодействия между фотонами, которые встречаются редко. В 2018 году исследователи Массачусетского технологического института объявили об открытии связанных триплетов фотонов, которые могут включать поляритоны . ^[127]^[128]

См. также [ править ]

Примечания [ править ]

↑ Хотя в переводе Нобелевской лекции Планка в Elsevier Планка интерпретируется 1967 года лихтквант как «фотон», более буквальный перевод 1922 года Ганса Тахера Кларка и Людвика Зильберштейна Планк, Макс (1922). «через Google Книги» . Возникновение и развитие квантовой теории . Clarendon Press - через Интернет-архив (archive.org, 01 марта 2007 г.). использует «квант света». Неизвестно никаких доказательств того, что сам Планк использовал термин «фотон» с 1926 года ( см. также ).
^ Азимов ^[12] приписывает Артуру Комптону определение квантов энергии как фотонов в 1923 году. ^[12]
^ Однако возможно, что система взаимодействует с третьей частицей или полем для аннигиляции с образованием одного фотона, поскольку третья частица или поле может поглощать импульс, равный и противоположный одиночному фотону, обеспечивая динамический баланс. Примером может служить случай, когда позитрон аннигилирует со связанным атомным электроном; в этом случае возможно испустить только один фотон, поскольку ядерное кулоновское поле нарушает трансляционную симметрию.
^ Фраза «независимо от того, насколько интенсивна» относится к интенсивности ниже примерно 10 ¹³ Вт/см ²в этот момент теория возмущений начинает разваливаться. Напротив, в интенсивном режиме, который для видимого света превышает примерно 10 ¹⁴ Вт/см ²Классическое волновое описание правильно предсказывает энергию, приобретаемую электронами, называемую пондеромоторной энергией . ^[49] Для сравнения, солнечный свет составляет всего около 0,1 Вт/см. ².
^ Эти эксперименты дают результаты, которые не могут быть объяснены никакой классической теорией света, поскольку они включают антикорреляции, возникающие в результате процесса квантовых измерений . В 1974 году первый такой эксперимент провел Клаузер, который сообщил о нарушении классического неравенства Коши-Шварца . В 1977 году Кимбл и др. продемонстрировал аналогичный эффект предотвращения группировки фотонов, взаимодействующих с светоделителем; этот подход был упрощен и источники ошибок устранены в эксперименте по антикорреляции фотонов Гранжером, Роджером и Аспектом (1986); ^[64]Эта работа рассмотрена и упрощена в работах Thorn, Neel и др. (2004). ^[65]
^ Впервые вопрос был сформулирован Теодором Дадделлом Ньютоном и Юджином Вигнером . ^[68]^[69]^[70]Проблемы возникают из-за фундаментальной природы группы Лоренца , которая описывает симметрию пространства-времени в специальной теории относительности. В отличие от генераторов преобразований Галилея , генераторы бустов Лоренца не коммутируют, поэтому одновременное присвоение низких неопределенностей всем координатам положения релятивистской частицы становится проблематичным. ^[71]

Ссылки [ править ]

^ Перейти обратно: ^а ^б ^с ^д ^Это ^ж Амслер, К.; и другие. ( Группа данных о частицах ) (2008). «Обзор физики элементарных частиц: калибровочные и бозоны Хиггса» (PDF) . Буквы по физике Б. 667 (1): 1. Бибкод : 2008PhLB..667....1A . дои : 10.1016/j.physletb.2008.07.018 . hdl : 1854/LU-685594 . S2CID 227119789 . Архивировано из оригинала 25 декабря 2018 г. Проверено 9 апреля 2010 г.
^ Йоос, Джордж (1951). Теоретическая физика . Лондон и Глазго: Blackie and Son Limited. п. 679.
^ Перейти обратно: ^а ^б «18 декабря 1926 года: Гилберт Льюис чеканит «фотон» в письме к природе» . www.aps.org . Архивировано из оригинала 2 мая 2019 г. Проверено 9 марта 2019 г.
^ «Гилберт Н. Льюис» . Фонд атомного наследия . Архивировано из оригинала 16 апреля 2015 г. Проверено 9 марта 2019 г.
^ Перейти обратно: ^а ^б ^с Краг, Хельге (2014). «Фотон: новый свет на старое имя». arXiv : 1401.0293 [ physical.hist-ph ].
^ Комптон, Артур Х. (1965) [12 декабря 1927 г.]. «Рентгеновские лучи как раздел оптики» (PDF) . Из Нобелевских лекций по физике 1922–1941 гг . Амстердам: Издательство Elsevier. Архивировано (PDF) из оригинала 12 мая 2024 года . Проверено 3 января 2019 г.
^ Кимбл, HJ; Дагенайс, М.; Мандель, Л. (1977). «Антигруппировка фотонов в резонансной флуоресценции» (PDF) . Письма о физических отзывах . 39 (11): 691–695. Бибкод : 1977PhRvL..39..691K . дои : 10.1103/PhysRevLett.39.691 . Архивировано (PDF) из оригинала 25 ноября 2020 г. Проверено 3 января 2019 г.
^ Гранжер, П.; Роджер, Г.; Аспект, А. (1986). «Экспериментальные доказательства эффекта антикорреляции фотонов на светоделителе: новый взгляд на однофотонные интерференции». Письма по еврофизике . 1 (4): 173–179. Бибкод : 1986EL......1..173G . CiteSeerX 10.1.1.178.4356 . дои : 10.1209/0295-5075/1/4/004 . S2CID 250837011 .
^ Краг, Хельге (1 декабря 2000 г.). «Макс Планк: сопротивляющийся революционер». Мир физики . 13 (12): 31–36. дои : 10.1088/2058-7058/13/12/34 .
^ Перейти обратно: ^а ^б ^с ^д Эйнштейн, Альберт (1905). «Об эвристической точке зрения на производство и преобразование света» (PDF) . Анналы физики (на немецком языке). 17 (6): 132–148. Бибкод : 1905АнП...322..132Е . дои : 10.1002/andp.19053220607 . Архивировано (PDF) из оригинала 24 сентября 2015 г. Проверено 25 августа 2010 г. Английский перевод доступен на Wikisource .
^ Льюис, Гилберт Н. (18 декабря 1926 г.). «Сохранение фотонов». Природа . 118 (2981): 874–875. Бибкод : 1926Natur.118..874L . дои : 10.1038/118874a0 . eISSN 1476-4687 . S2CID 4110026 . смотрите также
«Расхождения между экспериментом и электромагнитной теорией излучения». Написано в Брюсселе, Бельгия. Электроны и фотоны: Доклады и дискуссии пятого Физического совета, проходившего в Брюсселе с 24 по 29 октября 1927 года под эгидой Международного института физики Сольве . Пятый физический совет (на французском языке). Международный институт физики Сольвея (принимающее учреждение). Париж, Франция: Gauthier-Villars et Cie (опубликовано в 1928 г.). 24–29 октября 1927 г. с. 55–85. {{cite conference}}: CS1 maint: другие ( ссылка )
^ Перейти обратно: ^а ^б Азимов, Исаак (1983). Нейтрино: частица-призрак атома . Гарден-Сити, Нью-Йорк: Книги Эйвона. ISBN 978-0-380-00483-6 . и
Азимов, Исаак (1971). Вселенная: от плоской Земли до квазара . Нью-Йорк: Уокер . ISBN 978-0-8027-0316-3 . LCCN 66022515 .
^ Виллар, Пол Ульрих (1900). «Об отражении и преломлении катодных лучей и отклоняемых лучей радия». Отчеты сессий Академии наук (на французском языке). 130 : 1010–1012.
^ Виллар, Пол Ульрих (1900). «О радиевом излучении». Отчеты сессий Академии наук (на французском языке). 130 : 1178–1179.
^ Резерфорд, Эрнест ; Андраде, Эдвард, Северная Каролина (1914). «Длина волны мягких гамма-лучей радия Б» . Философский журнал . 27 (161): 854–868. дои : 10.1080/14786440508635156 . Архивировано из оригинала 08 марта 2020 г. Проверено 25 августа 2019 г.
^ Лиддл, Эндрю (2015). Введение в современную космологию . Джон Уайли и сыновья. п. 16. ISBN 978-1-118-69025-3 . Архивировано из оригинала 13 мая 2024 г. Проверено 27 февраля 2017 г.
^ Фриш, Дэвид Х .; Торндайк, Алан М. (1964). Элементарные частицы . Принстон, Нью-Джерси: Дэвид Ван Ностранд . п. 22.
^ Кобычев В.В.; Попов, С.Б. (2005). «Ограничения на заряд фотонов по наблюдениям внегалактических источников». Письма по астрономии . 31 (3): 147–151. arXiv : hep-ph/0411398 . Бибкод : 2005AstL...31..147K . дои : 10.1134/1.1883345 . S2CID 119409823 .
^ Баэз, Джон . «Какова масса фотона?» (перс. академический сайт). Калифорнийский университет Риверсайд . Архивировано из оригинала 31 мая 2014 г. Проверено 13 января 2009 г.
^ Ту, Лян-Чэн; Ло, Цзюнь; Гиллис, Джордж Т. (1 января 2005 г.). «Масса фотона» . Отчеты о прогрессе в физике . 68 (1): 77–130. Бибкод : 2005РПФ...68...77Т . дои : 10.1088/0034-4885/68/1/R02 . ISSN 0034-4885 .
^ Гольдхабер, Альфред Шарфф; Ньето, Майкл Мартин (23 марта 2010 г.). «Пределы масс фотонов и гравитонов» . Обзоры современной физики . 82 (1): 939–979. arXiv : 0809.1003 . Бибкод : 2010РвМП...82..939Г . дои : 10.1103/RevModPhys.82.939 . ISSN 0034-6861 . Архивировано из оригинала 13 мая 2024 г. Проверено 1 февраля 2024 г.
^ Хек, Джулиан (11 июля 2013 г.). «Насколько стабилен фотон?» . Письма о физических отзывах . 111 (2): 021801. arXiv : 1304.2821 . Бибкод : 2013PhRvL.111b1801H . doi : 10.1103/PhysRevLett.111.021801 . ISSN 0031-9007 . ПМИД 23889385 . Архивировано из оригинала 13 мая 2024 г. Проверено 1 февраля 2024 г.
^ Шварц, Мэтью Д. (2014). Квантовая теория поля и Стандартная модель . Издательство Кембриджского университета. п. 66. ИСБН 978-1-107-03473-0 .
^ «Роль калибровочного бозона и поляризации» §5.1 в Эйчисон, IJR; Привет, AJG (1993). Калибровочные теории в физике элементарных частиц . Издательство ИОП . ISBN 978-0-85274-328-7 . Архивировано из оригинала 17 января 2023 г. Проверено 6 октября 2016 г.
^ Амслер, К.; и другие. (2008). «Обзор физики элементарных частиц» (PDF) . Буквы по физике Б. 667 (1–5): 31. Бибкод : 2008PhLB..667....1A . дои : 10.1016/j.physletb.2008.07.018 . hdl : 1854/LU-685594 . ПМИД 10020536 . S2CID 227119789 . Архивировано (PDF) из оригинала 1 июня 2020 г. Проверено 26 октября 2017 г.
^ Перейти обратно: ^а ^б ^с Холлидей, Дэвид; Резник, Роберт; Уокер, Джерл (2005). Основы физики (7-е изд.). Джон Уайли и сыновья, Inc. ISBN 978-0-471-23231-5 .
^ См. Алонсо и Финн, 1968 , раздел 1.6.
^ Сопер, Дэвисон Э. «Электромагнитное излучение состоит из фотонов» . Институт теоретической науки. Университет Орегона . Архивировано из оригинала 8 апреля 2023 г. Проверено 21 марта 2024 г.
^ Хехт, Юджин (1998). Оптика (3-е изд.). Ридинг, Массачусетс; Харлоу: Аддисон-Уэсли. ISBN 978-0-201-83887-9 .
^ Раман, резюме ; Бхагавантам, С. (1931). «Экспериментальное доказательство вращения фотона» (PDF) . Индийский физический журнал . 6 (3244): 353. Бибкод : 1932Natur.129...22R . дои : 10.1038/129022a0 . hdl : 10821/664 . S2CID 4064852 . Архивировано из оригинала (PDF) 3 июня 2016 г. Проверено 28 декабря 2008 г.
^ Гриффитс, Дэвид Дж. (2008). Введение в элементарные частицы (2-е исправленное изд.). ВИЛИ-ВЧ. ISBN 978-3-527-40601-2 .
^ Алонсо и Финн 1968 , Раздел 9.3.
^ Борн, Макс; Блин-Стойл, Роджер Джон; Рэдклифф, Дж. М. (1989). «Приложение XXXII». Атомная физика . Курьерская корпорация. ISBN 978-0-486-65984-8 .
^ Мермин, Дэвид (февраль 1984 г.). «Относительность без света». Американский журнал физики . 52 (2): 119–124. Бибкод : 1984AmJPh..52..119M . дои : 10.1119/1.13917 .
^ Плимптон, С.; Лоутон, В. (1936). «Очень точная проверка закона силы Кулона между зарядами». Физический обзор . 50 (11): 1066. Бибкод : 1936PhRv...50.1066P . дои : 10.1103/PhysRev.50.1066 .
^ Уильямс, Э.; Фаллер, Дж.; Хилл, Х. (1971). «Новая экспериментальная проверка закона Кулона: лабораторный верхний предел массы покоя фотона». Письма о физических отзывах . 26 (12): 721. Бибкод : 1971PhRvL..26..721W . doi : 10.1103/PhysRevLett.26.721 .
^ Чибисов, Г.В. (1976). «Астрофизические верхние пределы массы покоя фотона». Успехи советской физики . 19 (7): 624. Бибкод : 1976СвФУ..19..624С . дои : 10.1070/PU1976v019n07ABEH005277 .
^ Озера, Родерик (1998). «Экспериментальные ограничения на массу фотона и космический магнитный векторный потенциал». Письма о физических отзывах . 80 (9): 1826. Бибкод : 1998PhRvL..80.1826L . doi : 10.1103/PhysRevLett.80.1826 .
^ Амслер, К; Дозер, М; Антонелли, М; Аснер, Д; Бабу, К; Баер, Х; Группа, Н; Барнетт, Р.; и другие. (2008). «Обзор физики элементарных частиц⁎» (PDF) . Буквы по физике Б. 667 (1–5): 1. Бибкод : 2008PhLB..667....1A . дои : 10.1016/j.physletb.2008.07.018 . hdl : 1854/LU-685594 . S2CID 227119789 . Архивировано (PDF) из оригинала 1 июня 2020 г. Проверено 26 октября 2017 г. Сводная таблица. Архивировано 9 января 2010 г. на Wayback Machine.
^ Адельбергер, Эрик; Двали, Гия; Грузинов, Андрей (2007). «Связь фотона и массы, разрушаемая вихрями». Письма о физических отзывах . 98 (1): 010402. arXiv : hep-ph/0306245 . Бибкод : 2007PhRvL..98a0402A . doi : 10.1103/PhysRevLett.98.010402 . ПМИД 17358459 . S2CID 31249827 .
^ Декарт, Рене (1637). Рассуждение о методе (на французском языке). Типография Яна Мэйра. ISBN 978-0-268-00870-3 .
^ Гук, Роберт (1667). Микрография: или некоторые физиологические описания мельчайших тел, сделанные с помощью увеличительных очков, с наблюдениями и последующими исследованиями ... Лондон, Великобритания: Лондонское королевское общество . ISBN 978-0-486-49564-4 . Архивировано из оригинала 2 декабря 2008 г. Проверено 26 сентября 2006 г.
^ Гюйгенс, Христиан (1678). Трактат о свете (на французском языке). . Английский перевод доступен в Project Gutenberg.
^ Перейти обратно: ^а ^б Ньютон, Исаак (1952) [1730]. Оптика (4-е изд.). Дувр, Нью-Йорк: Dover Publications. Книга II, часть III, положения XII–XX; Запросы 25–29. ISBN 978-0-486-60205-9 .
^ Бухвальд, Дж. З. (1989). «Возникновение волновой теории света: оптическая теория и эксперимент в начале девятнадцатого века» . Физика сегодня . 43 (4). Издательство Чикагского университета: 78–80. Бибкод : 1990ФТ....43д..78Б . дои : 10.1063/1.2810533 . ISBN 978-0-226-07886-1 . OCLC 18069573 .
^ Максвелл, Джеймс Клерк (1865). «Динамическая теория электромагнитного поля» . Философские труды Королевского общества . 155 : 459–512. Бибкод : 1865RSPT..155..459M . дои : 10.1098/rstl.1865.0008 . S2CID 186207827 . Эта статья последовала за выступлением Максвелла 8 декабря 1864 года перед Королевским обществом.
^ Герц, Генрих (1888). «О лучах электрической силы». Труды Прусской академии наук (на немецком языке). 1888 год . Берлин, Германия: 1297–1307 гг.
^ «Частотная зависимость люминесценции», стр. 276 и далее, §1.4 «фотоэлектрический эффект» в Alonso & Finn 1968 .
^ См. также: Борэм, Брюс В.; Хора, Генрих; Болтон, Пол Р. (1996). «Плотность фотонов и принцип соответствия электромагнитного взаимодействия». Материалы конференции AIP . 369 : 1234–1243. Бибкод : 1996AIPC..369.1234B . дои : 10.1063/1.50410 .
^ Перейти обратно: ^а ^б Вена, В. (1911). «Нобелевская лекция Вильгельма Вена» . nobelprize.org . Архивировано из оригинала 15 июля 2011 г. Проверено 25 августа 2006 г.
^ Планк, Макс (1901). «О законе распределения энергии в нормальном спектре» . Анналы физики (на немецком языке). 4 (3): 553–563. Стартовый код : 1901АнП...309..553П . дои : 10.1002/andp.19013090310 . английский перевод
^ Перейти обратно: ^а ^б Планк, Макс (1920). «Нобелевская лекция Макса Планка» . nobelprize.org. Архивировано из оригинала 15 июля 2011 г. Проверено 25 августа 2006 г.
^ Перейти обратно: ^а ^б ^с Эйнштейн, Альберт (1909). «О развитии наших взглядов на природу и состав радиации» (PDF) . Физический журнал (на немецком языке). 10 :817-825. Архивировано (PDF) из оригинала 7 июня 2011 г. Проверено 25 августа 2010 г. Английский перевод доступен на Wikisource .
^ Речь Сванте Аррениуса на Нобелевской премии по физике 1921 года, 10 декабря 1922 года. Текст в Интернете. Архивировано 4 сентября 2011 г. на Wayback Machine на сайте [nobelprize.org], Нобелевский фонд 2008 г. Дата доступа: 5 декабря 2008 г. .
^ Эйнштейн, Альберт (1916). «К квантовой теории излучения». Объявления Физического общества Цюриха (на немецком языке). 16 : 47. Также Physikalische Zeitschrift (на немецком языке), 18 , 121–128 (1917).
^ Перейти обратно: ^а ^б Комптон, Артур (1923). «Квантовая теория рассеяния рентгеновских лучей легкими элементами» . Физический обзор . 21 (5): 483–502. Бибкод : 1923PhRv...21..483C . дои : 10.1103/PhysRev.21.483 . Архивировано из оригинала 29 января 2018 г. Проверено 8 ноября 2020 г.
^ Перейти обратно: ^а ^б ^с Паис, А. (1982). Тонок Господь: Наука и жизнь Альберта Эйнштейна . Издательство Оксфордского университета. ISBN 978-0-19-853907-0 .
^ Перейти обратно: ^а ^б Милликен, Роберт А. (1924). «Нобелевская лекция Роберта А. Милликена» . Архивировано из оригинала 15 июля 2011 г. Проверено 25 августа 2006 г.
^ Хендри, Дж. (1980). «Развитие взглядов на корпускулярно-волновой дуализм света и квантовой теории, 1900–1920». Анналы науки . 37 (1): 59–79. дои : 10.1080/00033798000200121 .
^ Бор, Нильс ; Крамерс, Хендрик Энтони ; Слейтер, Джон К. (1924). «Квантовая теория излучения». Философский журнал . 47 (281): 785–802. дои : 10.1080/14786442408565262 . Также Журнал физики (на немецком языке), 24 , с. 69 (1924).
^ Ховард, Дон (декабрь 2004 г.). «Кто изобрел «Копенгагенскую интерпретацию»? Исследование мифологии». Философия науки . 71 (5): 669–682. дои : 10.1086/425941 . ISSN 0031-8248 . JSTOR 10.1086/425941 . S2CID 9454552 .
^ Гейзенберг, Вернер (1933). «Нобелевская лекция Гейзенберга» . Архивировано из оригинала 19 июля 2011 г. Проверено 11 сентября 2006 г.
^ Мандель, Леонард (1976). Вольф, Э. (ред.). Аргументы за и против полуклассической теории излучения . Прогресс в оптике . Том. 13. Северная Голландия. стр. 27–69. Бибкод : 1976ПрОпт..13...27М . дои : 10.1016/S0079-6638(08)70018-0 . ISBN 978-0-444-10806-7 . {{cite book}}: |journal= игнорируется ( помогите )
^ Гранжер, П.; Роджер, Г.; Аспект, А. (1986). «Экспериментальные доказательства эффекта антикорреляции фотонов на светоделителе: новый взгляд на однофотонные интерференции». Письма по еврофизике . 1 (4): 173–179. Бибкод : 1986EL......1..173G . CiteSeerX 10.1.1.178.4356 . дои : 10.1209/0295-5075/1/4/004 . S2CID 250837011 .
^ Торн, Джей-Джей; Нил, MS; Донато, Фольксваген; Бергрин, Г.С.; Дэвис, RE; Бек, М. (2004). «Наблюдение квантового поведения света в студенческой лаборатории» (PDF) . Американский журнал физики . 72 (9): 1210–1219. Бибкод : 2004AmJPh..72.1210T . дои : 10.1119/1.1737397 . Архивировано (PDF) из оригинала 1 февраля 2016 г. Проверено 29 июня 2009 г.
^ Тейлор, Джеффри Ингрэм (1909). Интерференционные полосы со слабым светом . Кембриджское философское общество. Труды Кембриджского философского общества . Том. 15. С. 114–115.
^ Салех, BEA и Тейх, MC (2007). Основы фотоники Уайли. ISBN 978-0-471-35832-9 .
^ Ньютон, Т.Д.; Вигнер, EP (1949). «Локализованные состояния элементарных частиц» (PDF) . Обзоры современной физики . 21 (3): 400–406. Бибкод : 1949РвМП...21..400Н . дои : 10.1103/RevModPhys.21.400 . Архивировано (PDF) из оригинала 16 мая 2023 г. Проверено 21 июня 2023 г.
^ Бялыницкий-Бирула, И. (1994). «О волновой функции фотона» . Acta Physica Polonica А. 86 (1–2): 97–116. Бибкод : 1994AcPPA..86...97B . doi : 10.12693/APhysPolA.86.97 .
^ Сайп, Дж. Э. (1995). «Волновые функции фотонов». Физический обзор А. 52 (3): 1875–1883. Бибкод : 1995PhRvA..52.1875S . doi : 10.1103/PhysRevA.52.1875 . ПМИД 9912446 .
^ Бялыницкий-Бирула, И. (1996). Волновая функция фотона . Прогресс в оптике . Том. 36. С. 245–294. Бибкод : 1996PrOpt..36..245B . дои : 10.1016/S0079-6638(08)70316-0 . ISBN 978-0-444-82530-8 . S2CID 17695022 . {{cite book}}: |journal= игнорируется ( помогите )
^ Перейти обратно: ^а ^б ^с Скалли, Миссури; Зубайри, М.С. (1997). Квантовая оптика . Кембридж, Англия: Издательство Кембриджского университета. ISBN 978-0-521-43595-6 . Архивировано из оригинала 13 мая 2024 г. Проверено 6 октября 2016 г.
^ Буш, Пол ; Лахти, Пекка; Вернер, Райнхард Ф. (17 октября 2013 г.). «Доказательство соотношения ошибки и возмущения Гейзенберга» (PDF) . Письма о физических отзывах . 111 (16): 160405. arXiv : 1306.1565 . Бибкод : 2013PhRvL.111p0405B . doi : 10.1103/PhysRevLett.111.160405 . ISSN 0031-9007 . ПМИД 24182239 . S2CID 24507489 .
^ Эпплби, Дэвид Маркус (6 мая 2016 г.). «Квантовые ошибки и возмущения: ответ Бушу, Лахти и Вернеру» . Энтропия . 18 (5): 174. arXiv : 1602.09002 . Бибкод : 2016Entrp..18..174A . дои : 10.3390/e18050174 .
^ Ландау, Лев Д. ; Лифшиц, Евгений М. (1977). Квантовая механика: нерелятивистская теория . Том. 3 (3-е изд.). Пергамон Пресс . ISBN 978-0-08-020940-1 . ОСЛК 2284121 .
^ Буш, П.; Грабовский, М.; Лахти, П.Дж. (январь 1995 г.). «Кто боится мер POV? Единый подход к наблюдаемым квантовой фазы». Анналы физики . 237 (1): 1–11. Бибкод : 1995АнФиз.237....1Б . дои : 10.1006/aphy.1995.1001 .
^ Бозе, Сатьендра Натх (1924). «Закон Планка и квантовая гипотеза света». Журнал физики (на немецком языке). 26 (1): 178–181. Бибкод : 1924ZPhy...26..178B . дои : 10.1007/BF01327326 . S2CID 186235974 .
^ Эйнштейн, Альберт (1924). «Квантовая теория одноатомного идеального газа». Известия Прусской академии наук (Берлин), физико-математический класс (на немецком языке). 1924 : 261–267.
^ Эйнштейн, Альберт (1925). Квантовая теория одноатомного идеального газа, второй трактат (на немецком языке). Том 1925. С. 3–14. дои : 10.1002/3527608958.ch28 . ISBN 978-3-527-60895-9 . {{cite book}}: |journal= игнорируется ( помогите )
^ Андерсон, Миннесота; Эншер, младший; Мэтьюз, MR; Виман, Карл Э .; Корнелл, Эрик Аллин (1995). «Наблюдение бозе-эйнштейновской конденсации в разбавленном атомном паре». Наука . 269 (5221): 198–201. Бибкод : 1995Sci...269..198A . дои : 10.1126/science.269.5221.198 . JSTOR 2888436 . ПМИД 17789847 . S2CID 540834 .
^ Кунео, Майкл (18 февраля 1999 г.). «Физики замедляют скорость света» . Гарвардская газета . Архивировано из оригинала 15 октября 2000 г. Проверено 7 декабря 2023 г.
^ «Свет превратился в материю, затем остановился и начал двигаться» . www.photonics.com . Архивировано из оригинала 02 апреля 2019 г. Проверено 7 декабря 2023 г.
^ Стритер, РФ; Вайтман, А.С. (1989). РСТ, спин и статистика и все такое . Аддисон-Уэсли. ISBN 978-0-201-09410-7 .
^ Эйнштейн, Альберт (1916). «Испускание и поглощение радиации согласно квантовой теории». Переговоры Немецкого физического общества (на немецком языке). 18 :318-323. Бибкод : 1916DPhyG..18..318E .
^ Уилсон, Дж.; Хоукс, FJB (1987). Лазеры: принципы и применение . Нью-Йорк: Прентис Холл. Раздел 1.4. ISBN 978-0-13-523705-2 .
^ Эйнштейн, Альберт (1916). «Испускание и поглощение радиации согласно квантовой теории». Переговоры Немецкого физического общества (на немецком языке). 18 :318-323. Бибкод : 1916DPhyG..18..318E . п. 322: Константы $A_{m}^{n}$ и $B_{m}^{n}$ можно было бы рассчитать напрямую, если бы мы владели электродинамикой и механикой, модифицированными в смысле квантовой гипотезы».
^ Дирак, Поль AM (1926). «К теории квантовой механики» . Труды Королевского общества А. 112 (762): 661–677. Бибкод : 1926RSPSA.112..661D . дои : 10.1098/rspa.1926.0133 .
^ Перейти обратно: ^а ^б Дирак, Поль AM (1927). «Квантовая теория испускания и поглощения излучения» . Труды Королевского общества А. 114 (767): 243–265. Бибкод : 1927RSPSA.114..243D . дои : 10.1098/rspa.1927.0039 .
^ Перейти обратно: ^а ^б Дирак, Поль AM (1927b). «Квантовая теория дисперсии» . Труды Королевского общества А. 114 (769): 710–728. Бибкод : 1927RSPSA.114..710D . дои : 10.1098/rspa.1927.0071 .
^ Гейзенберг, Вернер ; Паули, Вольфганг (1929). «К квантовой теории волновых полей». Журнал физики (на немецком языке). 56 (1–2): 1. Бибкод : 1929ZPhy...56....1H . дои : 10.1007/BF01340129 . S2CID 121928597 .
^ Гейзенберг, Вернер ; Паули, Вольфганг (1930). «К квантовой теории волновых полей». Журнал физики (на немецком языке). 59 (3–4): 139. Бибкод : 1930ZPhy...59..168H . дои : 10.1007/BF01341423 . S2CID 186219228 .
^ Ферми, Энрико (1932). «Квантовая теория излучения». Обзоры современной физики . 4 (1): 87. Бибкод : 1932РвМП....4...87Ф . дои : 10.1103/RevModPhys.4.87 .
^ Родился Макс (1926). «К квантовой механике столкновительных процессов». Журнал физики (на немецком языке). 37 (12): 863–867. Бибкод : 1926ZPhy...37..863B . дои : 10.1007/BF01397477 . S2CID 119896026 .
^ Родился Макс (1926). «Квантовая механика столкновительных процессов». Журнал физики (на немецком языке). 38 (11–12): 803. Бибкод : 1926ZPhy...38..803B . дои : 10.1007/BF01397184 . S2CID 126244962 .
^ Паис, А. (1986). Внутренняя граница: о материи и силах в физическом мире . Издательство Оксфордского университета. п. 260. ИСБН 978-0-19-851997-3 . В частности, Борн утверждал, что его вдохновили никогда не публиковавшиеся попытки Эйнштейна разработать теорию «призрачного поля», в которой точечные фотоны вероятностно направляются призрачными полями, которые следуют уравнениям Максвелла.
^ Дебай, Питер (1910). «Понятие вероятности в теории радиации» . Анналы физики (на немецком языке). 33 (16): 1427–1434. Бибкод : 1910АнП...338.1427Д . дои : 10.1002/andp.19103381617 . Архивировано из оригинала 14 марта 2020 г. Проверено 25 августа 2019 г.
^ Борн, Макс ; Гейзенберг, Вернер ; Джордан, Паскуаль (1925). «Квантовая механика II». Журнал физики (на немецком языке). 35 (8–9): 557–615. Бибкод : 1926ZPhy...35..557B . дои : 10.1007/BF01379806 . S2CID 186237037 .
^ Джагер, Грегг (2019). «Являются ли виртуальные частицы менее реальными?» (PDF) . Энтропия . 21 (2): 141. Бибкод : 2019Entrp..21..141J . дои : 10.3390/e21020141 . ПМЦ 7514619 . PMID 33266857 . Архивировано (PDF) из оригинала 11 июня 2023 г. Проверено 19 мая 2021 г.
^ Зи, Энтони (2003). Квантовая теория поля в двух словах . Принстон, Нью-Джерси: Издательство Принстонского университета . ISBN 0-691-01019-6 . OCLC 50479292 .
^ Ицыксон, К.; Зубер, Ж.-Б. (1980). Квантовая теория поля . МакГроу-Хилл. Фотон-фотонное рассеяние раздел 7–3–1, перенормировка глава 8–2. ISBN 978-0-07-032071-0 .
^ Вейглейн, Г. (2008). «Электрослабая физика в МЛЦ». Физический журнал: серия конференций . 110 (4): 042033. arXiv : 0711.3003 . Бибкод : 2008JPhCS.110d2033W . дои : 10.1088/1742-6596/110/4/042033 . S2CID 118517359 .
^ Перейти обратно: ^а ^б Райдер, Л.Х. (1996). Квантовая теория поля (2-е изд.). Англия: Издательство Кембриджского университета. ISBN 978-0-521-47814-4 .
↑ Нобелевская лекция Шелдона Глэшоу. Архивировано 18 апреля 2008 г. в Wayback Machine , прочитано 8 декабря 1979 г.
↑ Нобелевская лекция Абдуса Салама. Архивировано 18 апреля 2008 г. в Wayback Machine , прочитано 8 декабря 1979 г.
^ Нобелевская лекция Стивена Вайнберга. Архивировано 18 апреля 2008 г. в Wayback Machine , прочитано 8 декабря 1979 г.
^ Например, глава 14 в Хьюз, И.С. (1985). Элементарные частицы (2-е изд.). Издательство Кембриджского университета. ISBN 978-0-521-26092-3 .
^ Бауэр, TH; Спитал, РД; Йенни, доктор медицинских наук; Пипкин, FM (1978). «Адронные свойства фотона в высокоэнергетических взаимодействиях». Обзоры современной физики . 50 (2): 261. Бибкод : 1978РвМП...50..261Б . дои : 10.1103/RevModPhys.50.261 .
^ Сакураи, Джей-Джей (1960). «Теория сильных взаимодействий». Анналы физики . 11 (1): 1–48. Бибкод : 1960АнФиз..11....1С . дои : 10.1016/0003-4916(60)90126-3 .
^ Уолш, Т.Ф.; Зервас, П. (1973). «Двухфотонные процессы в партонной модели». Буквы по физике Б. 44 (2): 195. Бибкод : 1973PhLB...44..195W . дои : 10.1016/0370-2693(73)90520-0 .
^ Виттен, Э. (1977). «Аномальное сечение фотон-фотонного рассеяния в калибровочных теориях». Ядерная физика Б . 120 (2): 189–202. Бибкод : 1977НуФБ.120..189Вт . дои : 10.1016/0550-3213(77)90038-4 .
^ Нисиус, Р. (2000). «Структура фотонов в результате глубоконеупругого электрон-фотонного рассеяния». Отчеты по физике . 332 (4–6): 165–317. arXiv : hep-ex/9912049 . Бибкод : 2000ФР...332..165Н . дои : 10.1016/S0370-1573(99)00115-5 . S2CID 119437227 .
^ Например, раздел 10.1 в Данлэп, РА (2004). Введение в физику ядер и частиц . Брукс/Коул . ISBN 978-0-534-39294-9 .
^ Радиационная поправка к разделу массы электронов 7–1–2, разделу аномальных магнитных моментов 7–2–1, разделу лэмбовского сдвига 7–3–2 и сверхтонкому расщеплению в разделе позитрония 10–3 в Ицыксон, К.; Зубер, Ж.-Б. (1980). Квантовая теория поля . МакГроу-Хилл. ISBN 978-0-07-032071-0 .
^ Например, разделы 9.1 (гравитационный вклад фотонов) и 10.5 (влияние гравитации на свет) в Стефани, Х.; Стюарт, Дж. (1990). Общая теория относительности: введение в теорию гравитационного поля . Издательство Кембриджского университета. стр. 86 и далее, 108 и далее. ISBN 978-0-521-37941-0 .
^ Раздел «Поляритоны» 10.10.1, раздел «Комбинационное рассеяние света и Бриллюэна» 10.11.3 в Паттерсон, доктор медицинских наук; Бейли, Британская Колумбия (2007). Физика твердого тела: Введение в теорию . Спрингер . ISBN 978-3-540-24115-7 .
^ Найе, Р. (1998). Глазами Хаббла: рождение, жизнь и насильственная смерть звезд . ЦРК Пресс. ISBN 978-0-7503-0484-9 . ОСЛК 40180195 . Архивировано из оригинала 12 мая 2024 г. Проверено 6 октября 2016 г.
^ Купелис, Тео; Кун, Карл Ф. (2007). В поисках Вселенной . Джонс и Бартлетт Канада. п. 102. ИСБН 9780763743871 . Архивировано из оригинала 12 мая 2024 г. Проверено 29 ноября 2020 г.
^ Например, раздел 11-5 C в Сосна, Ш.; Хендриксон, Дж.Б.; Крам, диджей; Хаммонд, GS (1980). Органическая химия (4-е изд.). МакГроу-Хилл. ISBN 978-0-07-050115-7 .
↑ Нобелевская лекция, прочитанная Г. Уолдом 12 декабря 1967 года, на сайте nobelprize.org: Молекулярная основа зрительного возбуждения. Архивировано 23 апреля 2016 г. в Wayback Machine .
^ Раздел 1.1.10 «Фотоумножители», раздел «ПЗС-матрицы» 1.1.8, раздел «Счетчики Гейгера» 1.3.2.1 в Китчин, ЧР (2008). Астрофизические методы . Бока-Ратон, Флорида: CRC Press. ISBN 978-1-4200-8243-2 .
^ Уэймут, Джон (1971). Электроразрядные лампы . Кембридж, Массачусетс: MIT Press. ISBN 978-0-262-23048-3 .
^ Денк, В .; Свобода, К. (1997). «Фотонное превосходство: почему многофотонная визуализация — это больше, чем просто трюк» . Нейрон . 18 (3): 351–357. дои : 10.1016/S0896-6273(00)81237-4 . ПМИД 9115730 . S2CID 2414593 .
^ Лакович, младший (2006). Принципы флуоресцентной спектроскопии . Спрингер. стр. 529 и далее. ISBN 978-0-387-31278-1 .
^ Дженневейн, Т.; Ахляйтнер, У.; Вейс, Г.; Вайнфуртер, Х.; Цайлингер, А. (2000). «Быстрый и компактный квантовый генератор случайных чисел». Обзор научных инструментов . 71 (4): 1675–1680. arXiv : Quant-ph/9912118 . Бибкод : 2000RScI...71.1675J . дои : 10.1063/1.1150518 . S2CID 13118587 .
^ Стефанов А.; Гисин, Н.; Гуиннард, О.; Гуиннард, Л.; Збиден, Х. (2000). «Оптический квантовый генератор случайных чисел». Журнал современной оптики . 47 (4): 595–598. дои : 10.1080/095003400147908 .
^ Материалы вводного уровня по различным разделам квантовой оптики можно найти в Фокс, М. (2006). Квантовая оптика: Введение . Издательство Оксфордского университета. ISBN 978-0-19-856673-1 – через Google Книги.
^ Хигнетт, Кэтрин (16 февраля 2018 г.). «Физика создает новую форму света, которая может привести к революции в квантовых вычислениях» . Newsweek . Архивировано из оригинала 25 апреля 2021 года . Проверено 17 февраля 2018 г.
^ Лян, Ци-Юй; и другие. (16 февраля 2018 г.). «Наблюдение трехфотонных связанных состояний в квантовой нелинейной среде» . Наука . 359 (6377): 783–786. arXiv : 1709.01478 . Бибкод : 2018Sci...359..783L . дои : 10.1126/science.aao7293 . ПМК 6467536 . ПМИД 29449489 .

Дальнейшее чтение [ править ]

По дате публикации

Алонсо, М.; Финн, Э.Дж. (1968). Фундаментальная университетская физика . Том. III: Квантовая и статистическая физика. Аддисон-Уэсли. ISBN 978-0-201-00262-1 .
Клаузер, Дж. Ф. (1974). «Экспериментальное различие между квантовыми и классическими теоретико-полевыми предсказаниями фотоэлектрического эффекта» . Физический обзор D . 9 (4): 853–860. Бибкод : 1974PhRvD...9..853C . дои : 10.1103/PhysRevD.9.853 . S2CID 118320287 . Архивировано из оригинала 24 января 2019 г. Проверено 3 января 2019 г.
Паис, Авраам (1982). Тонок Господь: наука и жизнь Альберта Эйнштейна . Издательство Оксфордского университета.
Фейнман, Ричард (1985). КЭД: Странная теория света и материи . Издательство Принстонского университета. ISBN 978-0-691-12575-6 .
Гранжер, П.; Роджер, Г.; Аспект, А. (1986). «Экспериментальные доказательства эффекта антикорреляции фотонов на светоделителе: новый взгляд на однофотонные интерференции». Письма по еврофизике . 1 (4): 173–179. Бибкод : 1986EL......1..173G . CiteSeerX 10.1.1.178.4356 . дои : 10.1209/0295-5075/1/4/004 . S2CID 250837011 .
Лэмб, Уиллис Э. (1995). «Антифотон». Прикладная физика Б. 60 (2–3): 77–84. Бибкод : 1995ApPhB..60...77L . дои : 10.1007/BF01135846 . S2CID 263785760 .
«Специальный дополнительный выпуск» (PDF) . Новости оптики и фотоники . Том. 14 октября 2003 г. Архивировано из оригинала (PDF) 5 июня 2022 г.
- Ройчоудхури, К.; Раджарши, Р. (2003). «Природа света: Что такое фотон?». Новости оптики и фотоники . Том. 14. С. С1 (Приложение).
- Зайонц, А. (2003). «Свет переосмыслен». Новости оптики и фотоники . Том. 14. С. С2–С5 (Приложение).
- Лаудон, Р. (2003). «Что такое фотон?». Новости оптики и фотоники . Том. 14. С. С6–С11 (Приложение).
- Финкельштейн, Д. (2003). «Что такое фотон?». Новости оптики и фотоники . Том. 14. С. С12–С17 (Приложение).
- Мутукришнан, А.; Скалли, Миссури; Зубайри, М.С. (2003). «Понятие фотона – еще раз». Новости оптики и фотоники . Том. 14. С. С18–С27 (Приложение).
- Мак, Х.; Шляйх, Вольфганг П. (2003). «Фотон, наблюдаемый из фазового пространства Вигнера». Новости оптики и фотоники . Том. 14. С. С28–С35 (Приложение).
Глаубер, Р. (2005). «Сто лет световых квантов» (PDF) . Нобелевская премия . Лекция по физике. Архивировано из оригинала (PDF) 23 июля 2008 г. Проверено 29 июня 2009 г.
Хентшель, К. (2007). «Кванты света: созревание понятия путем поэтапного нарастания значения» . Физика и философия . 1 (2): 1–20. Архивировано из оригинала 29 мая 2014 г. Проверено 29 июня 2014 г.

Образование с одиночными фотонами

Торн, Джей-Джей; Нил, MS; Донато, Фольксваген; Бергрин, Г.С.; Дэвис, RE; Бек, М. (2004). «Наблюдение квантового поведения света в студенческой лаборатории» (PDF) . Американский журнал физики . 72 (9): 1210–1219. Бибкод : 2004AmJPh..72.1210T . дои : 10.1119/1.1737397 . Архивировано (PDF) из оригинала 1 февраля 2016 г. Проверено 29 июня 2009 г.
Броннер, П.; Струнц, Андреас; Силберхорн, Кристина; Мейн, Ян-Питер (2009). «Интерактивные экранные эксперименты с одиночными фотонами» . Европейский журнал физики . 30 (2): 345–353. Бибкод : 2009EJPh...30..345B . дои : 10.1088/0143-0807/30/2/014 . S2CID 38626417 . Архивировано из оригинала 1 июля 2019 г. Проверено 17 июля 2009 г.

Внешние ссылки [ править ]

Цитаты, связанные с Фотоном, в Wikiquote
Словарное определение фотона в Викисловаре
СМИ, связанные с Фотоном, на Викискладе?

[11] Хотя в переводе Нобелевской лекции Планка в Elsevier Планка интерпретируется 1967 года лихтквант как «фотон», более буквальный перевод 1922 года Ганса Тахера Кларка и Людвика Зильберштейна Планк, Макс (1922). «через Google Книги» . Возникновение и развитие квантовой теории . Clarendon Press - через Интернет-архив (archive.org, 01 марта 2007 г.). использует «квант света». Неизвестно никаких доказательств того, что сам Планк использовал термин «фотон» с 1926 года ( см. также ).

[14] Азимов ^[12] приписывает Артуру Комптону определение квантов энергии как фотонов в 1923 году. ^[12]

[33] Однако возможно, что система взаимодействует с третьей частицей или полем для аннигиляции с образованием одного фотона, поскольку третья частица или поле может поглощать импульс, равный и противоположный одиночному фотону, обеспечивая динамический баланс. Примером может служить случай, когда позитрон аннигилирует со связанным атомным электроном; в этом случае возможно испустить только один фотон, поскольку ядерное кулоновское поле нарушает трансляционную симметрию.

[53] Фраза «независимо от того, насколько интенсивна» относится к интенсивности ниже примерно 10 ¹³ Вт/см ²в этот момент теория возмущений начинает разваливаться. Напротив, в интенсивном режиме, который для видимого света превышает примерно 10 ¹⁴ Вт/см ²Классическое волновое описание правильно предсказывает энергию, приобретаемую электронами, называемую пондеромоторной энергией . ^[49] Для сравнения, солнечный свет составляет всего около 0,1 Вт/см. ².

[70] Эти эксперименты дают результаты, которые не могут быть объяснены никакой классической теорией света, поскольку они включают антикорреляции, возникающие в результате процесса квантовых измерений . В 1974 году первый такой эксперимент провел Клаузер, который сообщил о нарушении классического неравенства Коши-Шварца . В 1977 году Кимбл и др. продемонстрировал аналогичный эффект предотвращения группировки фотонов, взаимодействующих с светоделителем; этот подход был упрощен и источники ошибок устранены в эксперименте по антикорреляции фотонов Гранжером, Роджером и Аспектом (1986); ^[64]Эта работа рассмотрена и упрощена в работах Thorn, Neel и др. (2004). ^[65]

[77] Впервые вопрос был сформулирован Теодором Дадделлом Ньютоном и Юджином Вигнером . ^[68]^[69]^[70]Проблемы возникают из-за фундаментальной природы группы Лоренца , которая описывает симметрию пространства-времени в специальной теории относительности. В отличие от генераторов преобразований Галилея , генераторы бустов Лоренца не коммутируют, поэтому одновременное присвоение низких неопределенностей всем координатам положения релятивистской частицы становится проблематичным. ^[71]

[Particle_table_2009-1] Перейти обратно: ^а ^б ^с ^д ^Это ^ж Амслер, К.; и другие. ( Группа данных о частицах ) (2008). «Обзор физики элементарных частиц: калибровочные и бозоны Хиггса» (PDF) . Буквы по физике Б. 667 (1): 1. Бибкод : 2008PhLB..667....1A . дои : 10.1016/j.physletb.2008.07.018 . hdl : 1854/LU-685594 . S2CID 227119789 . Архивировано из оригинала 25 декабря 2018 г. Проверено 9 апреля 2010 г.

[2] Йоос, Джордж (1951). Теоретическая физика . Лондон и Глазго: Blackie and Son Limited. п. 679.

[www.aps.org-3] Перейти обратно: ^а ^б «18 декабря 1926 года: Гилберт Льюис чеканит «фотон» в письме к природе» . www.aps.org . Архивировано из оригинала 2 мая 2019 г. Проверено 9 марта 2019 г.

[4] «Гилберт Н. Льюис» . Фонд атомного наследия . Архивировано из оригинала 16 апреля 2015 г. Проверено 9 марта 2019 г.

[kragh-5] Перейти обратно: ^а ^б ^с Краг, Хельге (2014). «Фотон: новый свет на старое имя». arXiv : 1401.0293 [ physical.hist-ph ].

[compton-lecture-6] Комптон, Артур Х. (1965) [12 декабря 1927 г.]. «Рентгеновские лучи как раздел оптики» (PDF) . Из Нобелевских лекций по физике 1922–1941 гг . Амстердам: Издательство Elsevier. Архивировано (PDF) из оригинала 12 мая 2024 года . Проверено 3 января 2019 г.

[7] Кимбл, HJ; Дагенайс, М.; Мандель, Л. (1977). «Антигруппировка фотонов в резонансной флуоресценции» (PDF) . Письма о физических отзывах . 39 (11): 691–695. Бибкод : 1977PhRvL..39..691K . дои : 10.1103/PhysRevLett.39.691 . Архивировано (PDF) из оригинала 25 ноября 2020 г. Проверено 3 января 2019 г.

[8] Гранжер, П.; Роджер, Г.; Аспект, А. (1986). «Экспериментальные доказательства эффекта антикорреляции фотонов на светоделителе: новый взгляд на однофотонные интерференции». Письма по еврофизике . 1 (4): 173–179. Бибкод : 1986EL......1..173G . CiteSeerX 10.1.1.178.4356 . дои : 10.1209/0295-5075/1/4/004 . S2CID 250837011 .

[9] Краг, Хельге (1 декабря 2000 г.). «Макс Планк: сопротивляющийся революционер». Мир физики . 13 (12): 31–36. дои : 10.1088/2058-7058/13/12/34 .

[Einstein1905-10] Перейти обратно: ^а ^б ^с ^д Эйнштейн, Альберт (1905). «Об эвристической точке зрения на производство и преобразование света» (PDF) . Анналы физики (на немецком языке). 17 (6): 132–148. Бибкод : 1905АнП...322..132Е . дои : 10.1002/andp.19053220607 . Архивировано (PDF) из оригинала 24 сентября 2015 г. Проверено 25 августа 2010 г. Английский перевод доступен на Wikisource .

[12] Льюис, Гилберт Н. (18 декабря 1926 г.). «Сохранение фотонов». Природа . 118 (2981): 874–875. Бибкод : 1926Natur.118..874L . дои : 10.1038/118874a0 . eISSN 1476-4687 . S2CID 4110026 . смотрите также
«Расхождения между экспериментом и электромагнитной теорией излучения». Написано в Брюсселе, Бельгия. Электроны и фотоны: Доклады и дискуссии пятого Физического совета, проходившего в Брюсселе с 24 по 29 октября 1927 года под эгидой Международного института физики Сольве . Пятый физический совет (на французском языке). Международный институт физики Сольвея (принимающее учреждение). Париж, Франция: Gauthier-Villars et Cie (опубликовано в 1928 г.). 24–29 октября 1927 г. с. 55–85. {{cite conference}}: CS1 maint: другие ( ссылка )

[Asimov-1971-1983-13] Перейти обратно: ^а ^б Азимов, Исаак (1983). Нейтрино: частица-призрак атома . Гарден-Сити, Нью-Йорк: Книги Эйвона. ISBN 978-0-380-00483-6 . и
Азимов, Исаак (1971). Вселенная: от плоской Земли до квазара . Нью-Йорк: Уокер . ISBN 978-0-8027-0316-3 . LCCN 66022515 .

[15] Виллар, Пол Ульрих (1900). «Об отражении и преломлении катодных лучей и отклоняемых лучей радия». Отчеты сессий Академии наук (на французском языке). 130 : 1010–1012.

[16] Виллар, Пол Ульрих (1900). «О радиевом излучении». Отчеты сессий Академии наук (на французском языке). 130 : 1178–1179.

[17] Резерфорд, Эрнест ; Андраде, Эдвард, Северная Каролина (1914). «Длина волны мягких гамма-лучей радия Б» . Философский журнал . 27 (161): 854–868. дои : 10.1080/14786440508635156 . Архивировано из оригинала 08 марта 2020 г. Проверено 25 августа 2019 г.

[Liddle2015-18] Лиддл, Эндрю (2015). Введение в современную космологию . Джон Уайли и сыновья. п. 16. ISBN 978-1-118-69025-3 . Архивировано из оригинала 13 мая 2024 г. Проверено 27 февраля 2017 г.

[19] Фриш, Дэвид Х .; Торндайк, Алан М. (1964). Элементарные частицы . Принстон, Нью-Джерси: Дэвид Ван Ностранд . п. 22.

[chargeless-20] Кобычев В.В.; Попов, С.Б. (2005). «Ограничения на заряд фотонов по наблюдениям внегалактических источников». Письма по астрономии . 31 (3): 147–151. arXiv : hep-ph/0411398 . Бибкод : 2005AstL...31..147K . дои : 10.1134/1.1883345 . S2CID 119409823 .

[21] Баэз, Джон . «Какова масса фотона?» (перс. академический сайт). Калифорнийский университет Риверсайд . Архивировано из оригинала 31 мая 2014 г. Проверено 13 января 2009 г.

[22] Ту, Лян-Чэн; Ло, Цзюнь; Гиллис, Джордж Т. (1 января 2005 г.). «Масса фотона» . Отчеты о прогрессе в физике . 68 (1): 77–130. Бибкод : 2005РПФ...68...77Т . дои : 10.1088/0034-4885/68/1/R02 . ISSN 0034-4885 .

[23] Гольдхабер, Альфред Шарфф; Ньето, Майкл Мартин (23 марта 2010 г.). «Пределы масс фотонов и гравитонов» . Обзоры современной физики . 82 (1): 939–979. arXiv : 0809.1003 . Бибкод : 2010РвМП...82..939Г . дои : 10.1103/RevModPhys.82.939 . ISSN 0034-6861 . Архивировано из оригинала 13 мая 2024 г. Проверено 1 февраля 2024 г.

[24] Хек, Джулиан (11 июля 2013 г.). «Насколько стабилен фотон?» . Письма о физических отзывах . 111 (2): 021801. arXiv : 1304.2821 . Бибкод : 2013PhRvL.111b1801H . doi : 10.1103/PhysRevLett.111.021801 . ISSN 0031-9007 . ПМИД 23889385 . Архивировано из оригинала 13 мая 2024 г. Проверено 1 февраля 2024 г.

[Schwartz2014-25] Шварц, Мэтью Д. (2014). Квантовая теория поля и Стандартная модель . Издательство Кембриджского университета. п. 66. ИСБН 978-1-107-03473-0 .

[26] «Роль калибровочного бозона и поляризации» §5.1 в Эйчисон, IJR; Привет, AJG (1993). Калибровочные теории в физике элементарных частиц . Издательство ИОП . ISBN 978-0-85274-328-7 . Архивировано из оригинала 17 января 2023 г. Проверено 6 октября 2016 г.

[27] Амслер, К.; и другие. (2008). «Обзор физики элементарных частиц» (PDF) . Буквы по физике Б. 667 (1–5): 31. Бибкод : 2008PhLB..667....1A . дои : 10.1016/j.physletb.2008.07.018 . hdl : 1854/LU-685594 . ПМИД 10020536 . S2CID 227119789 . Архивировано (PDF) из оригинала 1 июня 2020 г. Проверено 26 октября 2017 г.

[Halliday-28] Перейти обратно: ^а ^б ^с Холлидей, Дэвид; Резник, Роберт; Уокер, Джерл (2005). Основы физики (7-е изд.). Джон Уайли и сыновья, Inc. ISBN 978-0-471-23231-5 .

[29] См. Алонсо и Финн, 1968 , раздел 1.6.

[30] Сопер, Дэвисон Э. «Электромагнитное излучение состоит из фотонов» . Институт теоретической науки. Университет Орегона . Архивировано из оригинала 8 апреля 2023 г. Проверено 21 марта 2024 г.

[Hecht-31] Хехт, Юджин (1998). Оптика (3-е изд.). Ридинг, Массачусетс; Харлоу: Аддисон-Уэсли. ISBN 978-0-201-83887-9 .

[spin-32] Раман, резюме ; Бхагавантам, С. (1931). «Экспериментальное доказательство вращения фотона» (PDF) . Индийский физический журнал . 6 (3244): 353. Бибкод : 1932Natur.129...22R . дои : 10.1038/129022a0 . hdl : 10821/664 . S2CID 4064852 . Архивировано из оригинала (PDF) 3 июня 2016 г. Проверено 28 декабря 2008 г.

[Griffiths2008-34] Гриффитс, Дэвид Дж. (2008). Введение в элементарные частицы (2-е исправленное изд.). ВИЛИ-ВЧ. ISBN 978-3-527-40601-2 .

[35] Алонсо и Финн 1968 , Раздел 9.3.

[36] Борн, Макс; Блин-Стойл, Роджер Джон; Рэдклифф, Дж. М. (1989). «Приложение XXXII». Атомная физика . Курьерская корпорация. ISBN 978-0-486-65984-8 .

[37] Мермин, Дэвид (февраль 1984 г.). «Относительность без света». Американский журнал физики . 52 (2): 119–124. Бибкод : 1984AmJPh..52..119M . дои : 10.1119/1.13917 .

[38] Плимптон, С.; Лоутон, В. (1936). «Очень точная проверка закона силы Кулона между зарядами». Физический обзор . 50 (11): 1066. Бибкод : 1936PhRv...50.1066P . дои : 10.1103/PhysRev.50.1066 .

[39] Уильямс, Э.; Фаллер, Дж.; Хилл, Х. (1971). «Новая экспериментальная проверка закона Кулона: лабораторный верхний предел массы покоя фотона». Письма о физических отзывах . 26 (12): 721. Бибкод : 1971PhRvL..26..721W . doi : 10.1103/PhysRevLett.26.721 .

[40] Чибисов, Г.В. (1976). «Астрофизические верхние пределы массы покоя фотона». Успехи советской физики . 19 (7): 624. Бибкод : 1976СвФУ..19..624С . дои : 10.1070/PU1976v019n07ABEH005277 .

[41] Озера, Родерик (1998). «Экспериментальные ограничения на массу фотона и космический магнитный векторный потенциал». Письма о физических отзывах . 80 (9): 1826. Бибкод : 1998PhRvL..80.1826L . doi : 10.1103/PhysRevLett.80.1826 .

[amsler-42] Амслер, К; Дозер, М; Антонелли, М; Аснер, Д; Бабу, К; Баер, Х; Группа, Н; Барнетт, Р.; и другие. (2008). «Обзор физики элементарных частиц⁎» (PDF) . Буквы по физике Б. 667 (1–5): 1. Бибкод : 2008PhLB..667....1A . дои : 10.1016/j.physletb.2008.07.018 . hdl : 1854/LU-685594 . S2CID 227119789 . Архивировано (PDF) из оригинала 1 июня 2020 г. Проверено 26 октября 2017 г. Сводная таблица. Архивировано 9 января 2010 г. на Wayback Machine.

[43] Адельбергер, Эрик; Двали, Гия; Грузинов, Андрей (2007). «Связь фотона и массы, разрушаемая вихрями». Письма о физических отзывах . 98 (1): 010402. arXiv : hep-ph/0306245 . Бибкод : 2007PhRvL..98a0402A . doi : 10.1103/PhysRevLett.98.010402 . ПМИД 17358459 . S2CID 31249827 .

[44] Декарт, Рене (1637). Рассуждение о методе (на французском языке). Типография Яна Мэйра. ISBN 978-0-268-00870-3 .

[45] Гук, Роберт (1667). Микрография: или некоторые физиологические описания мельчайших тел, сделанные с помощью увеличительных очков, с наблюдениями и последующими исследованиями ... Лондон, Великобритания: Лондонское королевское общество . ISBN 978-0-486-49564-4 . Архивировано из оригинала 2 декабря 2008 г. Проверено 26 сентября 2006 г.

[46] Гюйгенс, Христиан (1678). Трактат о свете (на французском языке). . Английский перевод доступен в Project Gutenberg.

[Newton1730-47] Перейти обратно: ^а ^б Ньютон, Исаак (1952) [1730]. Оптика (4-е изд.). Дувр, Нью-Йорк: Dover Publications. Книга II, часть III, положения XII–XX; Запросы 25–29. ISBN 978-0-486-60205-9 .

[48] Бухвальд, Дж. З. (1989). «Возникновение волновой теории света: оптическая теория и эксперимент в начале девятнадцатого века» . Физика сегодня . 43 (4). Издательство Чикагского университета: 78–80. Бибкод : 1990ФТ....43д..78Б . дои : 10.1063/1.2810533 . ISBN 978-0-226-07886-1 . OCLC 18069573 .

[maxwell-49] Максвелл, Джеймс Клерк (1865). «Динамическая теория электромагнитного поля» . Философские труды Королевского общества . 155 : 459–512. Бибкод : 1865RSPT..155..459M . дои : 10.1098/rstl.1865.0008 . S2CID 186207827 . Эта статья последовала за выступлением Максвелла 8 декабря 1864 года перед Королевским обществом.

[hertz-50] Герц, Генрих (1888). «О лучах электрической силы». Труды Прусской академии наук (на немецком языке). 1888 год . Берлин, Германия: 1297–1307 гг.

[51] «Частотная зависимость люминесценции», стр. 276 и далее, §1.4 «фотоэлектрический эффект» в Alonso & Finn 1968 .

[52] См. также: Борэм, Брюс В.; Хора, Генрих; Болтон, Пол Р. (1996). «Плотность фотонов и принцип соответствия электромагнитного взаимодействия». Материалы конференции AIP . 369 : 1234–1243. Бибкод : 1996AIPC..369.1234B . дои : 10.1063/1.50410 .

[Wien1911-54] Перейти обратно: ^а ^б Вена, В. (1911). «Нобелевская лекция Вильгельма Вена» . nobelprize.org . Архивировано из оригинала 15 июля 2011 г. Проверено 25 августа 2006 г.

[Planck1901-55] Планк, Макс (1901). «О законе распределения энергии в нормальном спектре» . Анналы физики (на немецком языке). 4 (3): 553–563. Стартовый код : 1901АнП...309..553П . дои : 10.1002/andp.19013090310 . английский перевод

[Planck1918-56] Перейти обратно: ^а ^б Планк, Макс (1920). «Нобелевская лекция Макса Планка» . nobelprize.org. Архивировано из оригинала 15 июля 2011 г. Проверено 25 августа 2006 г.

[Einstein1909-57] Перейти обратно: ^а ^б ^с Эйнштейн, Альберт (1909). «О развитии наших взглядов на природу и состав радиации» (PDF) . Физический журнал (на немецком языке). 10 :817-825. Архивировано (PDF) из оригинала 7 июня 2011 г. Проверено 25 августа 2010 г. Английский перевод доступен на Wikisource .

[58] Речь Сванте Аррениуса на Нобелевской премии по физике 1921 года, 10 декабря 1922 года. Текст в Интернете. Архивировано 4 сентября 2011 г. на Wayback Machine на сайте [nobelprize.org], Нобелевский фонд 2008 г. Дата доступа: 5 декабря 2008 г. .

[Einstein1916b-59] Эйнштейн, Альберт (1916). «К квантовой теории излучения». Объявления Физического общества Цюриха (на немецком языке). 16 : 47. Также Physikalische Zeitschrift (на немецком языке), 18 , 121–128 (1917).

[Compton1923-60] Перейти обратно: ^а ^б Комптон, Артур (1923). «Квантовая теория рассеяния рентгеновских лучей легкими элементами» . Физический обзор . 21 (5): 483–502. Бибкод : 1923PhRv...21..483C . дои : 10.1103/PhysRev.21.483 . Архивировано из оригинала 29 января 2018 г. Проверено 8 ноября 2020 г.

[Pais1982-61] Перейти обратно: ^а ^б ^с Паис, А. (1982). Тонок Господь: Наука и жизнь Альберта Эйнштейна . Издательство Оксфордского университета. ISBN 978-0-19-853907-0 .

[Millikan1923-62] Перейти обратно: ^а ^б Милликен, Роберт А. (1924). «Нобелевская лекция Роберта А. Милликена» . Архивировано из оригинала 15 июля 2011 г. Проверено 25 августа 2006 г.

[63] Хендри, Дж. (1980). «Развитие взглядов на корпускулярно-волновой дуализм света и квантовой теории, 1900–1920». Анналы науки . 37 (1): 59–79. дои : 10.1080/00033798000200121 .

[Bohr1924-64] Бор, Нильс ; Крамерс, Хендрик Энтони ; Слейтер, Джон К. (1924). «Квантовая теория излучения». Философский журнал . 47 (281): 785–802. дои : 10.1080/14786442408565262 . Также Журнал физики (на немецком языке), 24 , с. 69 (1924).

[65] Ховард, Дон (декабрь 2004 г.). «Кто изобрел «Копенгагенскую интерпретацию»? Исследование мифологии». Философия науки . 71 (5): 669–682. дои : 10.1086/425941 . ISSN 0031-8248 . JSTOR 10.1086/425941 . S2CID 9454552 .

[Heisenberg1932-66] Гейзенберг, Вернер (1933). «Нобелевская лекция Гейзенберга» . Архивировано из оригинала 19 июля 2011 г. Проверено 11 сентября 2006 г.

[Mandel1976-67] Мандель, Леонард (1976). Вольф, Э. (ред.). Аргументы за и против полуклассической теории излучения . Прогресс в оптике . Том. 13. Северная Голландия. стр. 27–69. Бибкод : 1976ПрОпт..13...27М . дои : 10.1016/S0079-6638(08)70018-0 . ISBN 978-0-444-10806-7 . {{cite book}}: |journal= игнорируется ( помогите )

[68] Гранжер, П.; Роджер, Г.; Аспект, А. (1986). «Экспериментальные доказательства эффекта антикорреляции фотонов на светоделителе: новый взгляд на однофотонные интерференции». Письма по еврофизике . 1 (4): 173–179. Бибкод : 1986EL......1..173G . CiteSeerX 10.1.1.178.4356 . дои : 10.1209/0295-5075/1/4/004 . S2CID 250837011 .

[69] Торн, Джей-Джей; Нил, MS; Донато, Фольксваген; Бергрин, Г.С.; Дэвис, RE; Бек, М. (2004). «Наблюдение квантового поведения света в студенческой лаборатории» (PDF) . Американский журнал физики . 72 (9): 1210–1219. Бибкод : 2004AmJPh..72.1210T . дои : 10.1119/1.1737397 . Архивировано (PDF) из оригинала 1 февраля 2016 г. Проверено 29 июня 2009 г.

[Taylor1909-71] Тейлор, Джеффри Ингрэм (1909). Интерференционные полосы со слабым светом . Кембриджское философское общество. Труды Кембриджского философского общества . Том. 15. С. 114–115.

[Saleh-72] Салех, BEA и Тейх, MC (2007). Основы фотоники Уайли. ISBN 978-0-471-35832-9 .

[73] Ньютон, Т.Д.; Вигнер, EP (1949). «Локализованные состояния элементарных частиц» (PDF) . Обзоры современной физики . 21 (3): 400–406. Бибкод : 1949РвМП...21..400Н . дои : 10.1103/RevModPhys.21.400 . Архивировано (PDF) из оригинала 16 мая 2023 г. Проверено 21 июня 2023 г.

[74] Бялыницкий-Бирула, И. (1994). «О волновой функции фотона» . Acta Physica Polonica А. 86 (1–2): 97–116. Бибкод : 1994AcPPA..86...97B . doi : 10.12693/APhysPolA.86.97 .

[75] Сайп, Дж. Э. (1995). «Волновые функции фотонов». Физический обзор А. 52 (3): 1875–1883. Бибкод : 1995PhRvA..52.1875S . doi : 10.1103/PhysRevA.52.1875 . ПМИД 9912446 .

[76] Бялыницкий-Бирула, И. (1996). Волновая функция фотона . Прогресс в оптике . Том. 36. С. 245–294. Бибкод : 1996PrOpt..36..245B . дои : 10.1016/S0079-6638(08)70316-0 . ISBN 978-0-444-82530-8 . S2CID 17695022 . {{cite book}}: |journal= игнорируется ( помогите )

[scully1997-78] Перейти обратно: ^а ^б ^с Скалли, Миссури; Зубайри, М.С. (1997). Квантовая оптика . Кембридж, Англия: Издательство Кембриджского университета. ISBN 978-0-521-43595-6 . Архивировано из оригинала 13 мая 2024 г. Проверено 6 октября 2016 г.

[79] Буш, Пол ; Лахти, Пекка; Вернер, Райнхард Ф. (17 октября 2013 г.). «Доказательство соотношения ошибки и возмущения Гейзенберга» (PDF) . Письма о физических отзывах . 111 (16): 160405. arXiv : 1306.1565 . Бибкод : 2013PhRvL.111p0405B . doi : 10.1103/PhysRevLett.111.160405 . ISSN 0031-9007 . ПМИД 24182239 . S2CID 24507489 .

[80] Эпплби, Дэвид Маркус (6 мая 2016 г.). «Квантовые ошибки и возмущения: ответ Бушу, Лахти и Вернеру» . Энтропия . 18 (5): 174. arXiv : 1602.09002 . Бибкод : 2016Entrp..18..174A . дои : 10.3390/e18050174 .

[L&L-81] Ландау, Лев Д. ; Лифшиц, Евгений М. (1977). Квантовая механика: нерелятивистская теория . Том. 3 (3-е изд.). Пергамон Пресс . ISBN 978-0-08-020940-1 . ОСЛК 2284121 .

[82] Буш, П.; Грабовский, М.; Лахти, П.Дж. (январь 1995 г.). «Кто боится мер POV? Единый подход к наблюдаемым квантовой фазы». Анналы физики . 237 (1): 1–11. Бибкод : 1995АнФиз.237....1Б . дои : 10.1006/aphy.1995.1001 .

[Bose1924-83] Бозе, Сатьендра Натх (1924). «Закон Планка и квантовая гипотеза света». Журнал физики (на немецком языке). 26 (1): 178–181. Бибкод : 1924ZPhy...26..178B . дои : 10.1007/BF01327326 . S2CID 186235974 .

[Einstein1924-84] Эйнштейн, Альберт (1924). «Квантовая теория одноатомного идеального газа». Известия Прусской академии наук (Берлин), физико-математический класс (на немецком языке). 1924 : 261–267.

[Einstein1925-85] Эйнштейн, Альберт (1925). Квантовая теория одноатомного идеального газа, второй трактат (на немецком языке). Том 1925. С. 3–14. дои : 10.1002/3527608958.ch28 . ISBN 978-3-527-60895-9 . {{cite book}}: |journal= игнорируется ( помогите )

[86] Андерсон, Миннесота; Эншер, младший; Мэтьюз, MR; Виман, Карл Э .; Корнелл, Эрик Аллин (1995). «Наблюдение бозе-эйнштейновской конденсации в разбавленном атомном паре». Наука . 269 (5221): 198–201. Бибкод : 1995Sci...269..198A . дои : 10.1126/science.269.5221.198 . JSTOR 2888436 . ПМИД 17789847 . S2CID 540834 .

[87] Кунео, Майкл (18 февраля 1999 г.). «Физики замедляют скорость света» . Гарвардская газета . Архивировано из оригинала 15 октября 2000 г. Проверено 7 декабря 2023 г.

[88] «Свет превратился в материю, затем остановился и начал двигаться» . www.photonics.com . Архивировано из оригинала 02 апреля 2019 г. Проверено 7 декабря 2023 г.

[89] Стритер, РФ; Вайтман, А.С. (1989). РСТ, спин и статистика и все такое . Аддисон-Уэсли. ISBN 978-0-201-09410-7 .

[Einstein1916a-90] Эйнштейн, Альберт (1916). «Испускание и поглощение радиации согласно квантовой теории». Переговоры Немецкого физического общества (на немецком языке). 18 :318-323. Бибкод : 1916DPhyG..18..318E .

[91] Уилсон, Дж.; Хоукс, FJB (1987). Лазеры: принципы и применение . Нью-Йорк: Прентис Холл. Раздел 1.4. ISBN 978-0-13-523705-2 .

[92] Эйнштейн, Альберт (1916). «Испускание и поглощение радиации согласно квантовой теории». Переговоры Немецкого физического общества (на немецком языке). 18 :318-323. Бибкод : 1916DPhyG..18..318E . п. 322: Константы $A_{m}^{n}$ и $B_{m}^{n}$ можно было бы рассчитать напрямую, если бы мы владели электродинамикой и механикой, модифицированными в смысле квантовой гипотезы».

[Dirac1926-93] Дирак, Поль AM (1926). «К теории квантовой механики» . Труды Королевского общества А. 112 (762): 661–677. Бибкод : 1926RSPSA.112..661D . дои : 10.1098/rspa.1926.0133 .

[Dirac1927a-94] Перейти обратно: ^а ^б Дирак, Поль AM (1927). «Квантовая теория испускания и поглощения излучения» . Труды Королевского общества А. 114 (767): 243–265. Бибкод : 1927RSPSA.114..243D . дои : 10.1098/rspa.1927.0039 .

[Dirac1927b-95] Перейти обратно: ^а ^б Дирак, Поль AM (1927b). «Квантовая теория дисперсии» . Труды Королевского общества А. 114 (769): 710–728. Бибкод : 1927RSPSA.114..710D . дои : 10.1098/rspa.1927.0071 .

[Heisenberg1929-96] Гейзенберг, Вернер ; Паули, Вольфганг (1929). «К квантовой теории волновых полей». Журнал физики (на немецком языке). 56 (1–2): 1. Бибкод : 1929ZPhy...56....1H . дои : 10.1007/BF01340129 . S2CID 121928597 .

[Heisenberg1930-97] Гейзенберг, Вернер ; Паули, Вольфганг (1930). «К квантовой теории волновых полей». Журнал физики (на немецком языке). 59 (3–4): 139. Бибкод : 1930ZPhy...59..168H . дои : 10.1007/BF01341423 . S2CID 186219228 .

[Fermi1932-98] Ферми, Энрико (1932). «Квантовая теория излучения». Обзоры современной физики . 4 (1): 87. Бибкод : 1932РвМП....4...87Ф . дои : 10.1103/RevModPhys.4.87 .

[Born1926a-99] Родился Макс (1926). «К квантовой механике столкновительных процессов». Журнал физики (на немецком языке). 37 (12): 863–867. Бибкод : 1926ZPhy...37..863B . дои : 10.1007/BF01397477 . S2CID 119896026 .

[Born1926b-100] Родился Макс (1926). «Квантовая механика столкновительных процессов». Журнал физики (на немецком языке). 38 (11–12): 803. Бибкод : 1926ZPhy...38..803B . дои : 10.1007/BF01397184 . S2CID 126244962 .

[ghost_field-101] Паис, А. (1986). Внутренняя граница: о материи и силах в физическом мире . Издательство Оксфордского университета. п. 260. ИСБН 978-0-19-851997-3 . В частности, Борн утверждал, что его вдохновили никогда не публиковавшиеся попытки Эйнштейна разработать теорию «призрачного поля», в которой точечные фотоны вероятностно направляются призрачными полями, которые следуют уравнениям Максвелла.

[Debye1910-102] Дебай, Питер (1910). «Понятие вероятности в теории радиации» . Анналы физики (на немецком языке). 33 (16): 1427–1434. Бибкод : 1910АнП...338.1427Д . дои : 10.1002/andp.19103381617 . Архивировано из оригинала 14 марта 2020 г. Проверено 25 августа 2019 г.

[Born1925-103] Борн, Макс ; Гейзенберг, Вернер ; Джордан, Паскуаль (1925). «Квантовая механика II». Журнал физики (на немецком языке). 35 (8–9): 557–615. Бибкод : 1926ZPhy...35..557B . дои : 10.1007/BF01379806 . S2CID 186237037 .

[104] Джагер, Грегг (2019). «Являются ли виртуальные частицы менее реальными?» (PDF) . Энтропия . 21 (2): 141. Бибкод : 2019Entrp..21..141J . дои : 10.3390/e21020141 . ПМЦ 7514619 . PMID 33266857 . Архивировано (PDF) из оригинала 11 июня 2023 г. Проверено 19 мая 2021 г.

[105] Зи, Энтони (2003). Квантовая теория поля в двух словах . Принстон, Нью-Джерси: Издательство Принстонского университета . ISBN 0-691-01019-6 . OCLC 50479292 .

[106] Ицыксон, К.; Зубер, Ж.-Б. (1980). Квантовая теория поля . МакГроу-Хилл. Фотон-фотонное рассеяние раздел 7–3–1, перенормировка глава 8–2. ISBN 978-0-07-032071-0 .

[107] Вейглейн, Г. (2008). «Электрослабая физика в МЛЦ». Физический журнал: серия конференций . 110 (4): 042033. arXiv : 0711.3003 . Бибкод : 2008JPhCS.110d2033W . дои : 10.1088/1742-6596/110/4/042033 . S2CID 118517359 .

[Ryder-108] Перейти обратно: ^а ^б Райдер, Л.Х. (1996). Квантовая теория поля (2-е изд.). Англия: Издательство Кембриджского университета. ISBN 978-0-521-47814-4 .

[Glashow-109] Нобелевская лекция Шелдона Глэшоу. Архивировано 18 апреля 2008 г. в Wayback Machine , прочитано 8 декабря 1979 г.

[Salam-110] Нобелевская лекция Абдуса Салама. Архивировано 18 апреля 2008 г. в Wayback Machine , прочитано 8 декабря 1979 г.

[Weinberg-111] Нобелевская лекция Стивена Вайнберга. Архивировано 18 апреля 2008 г. в Wayback Machine , прочитано 8 декабря 1979 г.

[112] Например, глава 14 в Хьюз, И.С. (1985). Элементарные частицы (2-е изд.). Издательство Кембриджского университета. ISBN 978-0-521-26092-3 .

[113] Бауэр, TH; Спитал, РД; Йенни, доктор медицинских наук; Пипкин, FM (1978). «Адронные свойства фотона в высокоэнергетических взаимодействиях». Обзоры современной физики . 50 (2): 261. Бибкод : 1978РвМП...50..261Б . дои : 10.1103/RevModPhys.50.261 .

[114] Сакураи, Джей-Джей (1960). «Теория сильных взаимодействий». Анналы физики . 11 (1): 1–48. Бибкод : 1960АнФиз..11....1С . дои : 10.1016/0003-4916(60)90126-3 .

[115] Уолш, Т.Ф.; Зервас, П. (1973). «Двухфотонные процессы в партонной модели». Буквы по физике Б. 44 (2): 195. Бибкод : 1973PhLB...44..195W . дои : 10.1016/0370-2693(73)90520-0 .

[116] Виттен, Э. (1977). «Аномальное сечение фотон-фотонного рассеяния в калибровочных теориях». Ядерная физика Б . 120 (2): 189–202. Бибкод : 1977НуФБ.120..189Вт . дои : 10.1016/0550-3213(77)90038-4 .

[117] Нисиус, Р. (2000). «Структура фотонов в результате глубоконеупругого электрон-фотонного рассеяния». Отчеты по физике . 332 (4–6): 165–317. arXiv : hep-ex/9912049 . Бибкод : 2000ФР...332..165Н . дои : 10.1016/S0370-1573(99)00115-5 . S2CID 119437227 .

[118] Например, раздел 10.1 в Данлэп, РА (2004). Введение в физику ядер и частиц . Брукс/Коул . ISBN 978-0-534-39294-9 .

[119] Радиационная поправка к разделу массы электронов 7–1–2, разделу аномальных магнитных моментов 7–2–1, разделу лэмбовского сдвига 7–3–2 и сверхтонкому расщеплению в разделе позитрония 10–3 в Ицыксон, К.; Зубер, Ж.-Б. (1980). Квантовая теория поля . МакГроу-Хилл. ISBN 978-0-07-032071-0 .

[120] Например, разделы 9.1 (гравитационный вклад фотонов) и 10.5 (влияние гравитации на свет) в Стефани, Х.; Стюарт, Дж. (1990). Общая теория относительности: введение в теорию гравитационного поля . Издательство Кембриджского университета. стр. 86 и далее, 108 и далее. ISBN 978-0-521-37941-0 .

[121] Раздел «Поляритоны» 10.10.1, раздел «Комбинационное рассеяние света и Бриллюэна» 10.11.3 в Паттерсон, доктор медицинских наук; Бейли, Британская Колумбия (2007). Физика твердого тела: Введение в теорию . Спрингер . ISBN 978-3-540-24115-7 .

[122] Найе, Р. (1998). Глазами Хаббла: рождение, жизнь и насильственная смерть звезд . ЦРК Пресс. ISBN 978-0-7503-0484-9 . ОСЛК 40180195 . Архивировано из оригинала 12 мая 2024 г. Проверено 6 октября 2016 г.

[123] Купелис, Тео; Кун, Карл Ф. (2007). В поисках Вселенной . Джонс и Бартлетт Канада. п. 102. ИСБН 9780763743871 . Архивировано из оригинала 12 мая 2024 г. Проверено 29 ноября 2020 г.

[124] Например, раздел 11-5 C в Сосна, Ш.; Хендриксон, Дж.Б.; Крам, диджей; Хаммонд, GS (1980). Органическая химия (4-е изд.). МакГроу-Хилл. ISBN 978-0-07-050115-7 .

[125] Нобелевская лекция, прочитанная Г. Уолдом 12 декабря 1967 года, на сайте nobelprize.org: Молекулярная основа зрительного возбуждения. Архивировано 23 апреля 2016 г. в Wayback Machine .

[126] Раздел 1.1.10 «Фотоумножители», раздел «ПЗС-матрицы» 1.1.8, раздел «Счетчики Гейгера» 1.3.2.1 в Китчин, ЧР (2008). Астрофизические методы . Бока-Ратон, Флорида: CRC Press. ISBN 978-1-4200-8243-2 .

[127] Уэймут, Джон (1971). Электроразрядные лампы . Кембридж, Массачусетс: MIT Press. ISBN 978-0-262-23048-3 .

[128] Денк, В .; Свобода, К. (1997). «Фотонное превосходство: почему многофотонная визуализация — это больше, чем просто трюк» . Нейрон . 18 (3): 351–357. дои : 10.1016/S0896-6273(00)81237-4 . ПМИД 9115730 . S2CID 2414593 .

[129] Лакович, младший (2006). Принципы флуоресцентной спектроскопии . Спрингер. стр. 529 и далее. ISBN 978-0-387-31278-1 .

[130] Дженневейн, Т.; Ахляйтнер, У.; Вейс, Г.; Вайнфуртер, Х.; Цайлингер, А. (2000). «Быстрый и компактный квантовый генератор случайных чисел». Обзор научных инструментов . 71 (4): 1675–1680. arXiv : Quant-ph/9912118 . Бибкод : 2000RScI...71.1675J . дои : 10.1063/1.1150518 . S2CID 13118587 .

[131] Стефанов А.; Гисин, Н.; Гуиннард, О.; Гуиннард, Л.; Збиден, Х. (2000). «Оптический квантовый генератор случайных чисел». Журнал современной оптики . 47 (4): 595–598. дои : 10.1080/095003400147908 .

[132] Материалы вводного уровня по различным разделам квантовой оптики можно найти в Фокс, М. (2006). Квантовая оптика: Введение . Издательство Оксфордского университета. ISBN 978-0-19-856673-1 – через Google Книги.

[NW-20180216-133] Хигнетт, Кэтрин (16 февраля 2018 г.). «Физика создает новую форму света, которая может привести к революции в квантовых вычислениях» . Newsweek . Архивировано из оригинала 25 апреля 2021 года . Проверено 17 февраля 2018 г.

[SCI-20180216-134] Лян, Ци-Юй; и другие. (16 февраля 2018 г.). «Наблюдение трехфотонных связанных состояний в квантовой нелинейной среде» . Наука . 359 (6377): 783–786. arXiv : 1709.01478 . Бибкод : 2018Sci...359..783L . дои : 10.1126/science.aao7293 . ПМК 6467536 . ПМИД 29449489 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[а]

[11]

[б]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[с]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[д]

[50]

[51]

[52]

[53]

[54]

[55]

[56]

[57]

[58]

[59]

[60]

[61]

[62]

[63]

[Это]

[66]

[67]

[ф]

[72]

[73]

[74]

[75]

[76]

[77]

[78]

[79]

[80]

[81]

[82]

[83]

[84]

[85]

[86]

[87]

[88]

[89]

[90]

[91]

[92]

[93]

[94]

[95]

[96]

[97]

[98]

[99]

[100]

[101]

[102]

v т Это Квантовая электродинамика
Formalism	Euler–Heisenberg Lagrangian Feynman diagram Gupta–Bleuler formalism Path integral formulation
Particles	Dual photon Electron Faddeev–Popov ghost Photon Positron Positronium Virtual particles
Concepts	Anomalous magnetic dipole moment Furry's theorem Klein–Nishina formula Landau pole QED vacuum Self-energy Schwinger limit Uehling potential Vacuum polarization Vertex function Ward–Takahashi identity
Processes	Bhabha scattering Breit–Wheeler process Bremsstrahlung Compton scattering Delbrück scattering Lamb shift Møller scattering Schwinger effect Photon-photon scattering
See also: Template:Quantum mechanics topics

Базы данных авторитетного контроля
National	France BnF data Germany Israel United States Japan Czech Republic
Other	IdRef