группа Лоренца

В физике и математике — группа Лоренца это группа всех преобразований Лоренца , пространства-времени Минковского классическая и квантовая установка для всех (негравитационных) физических явлений . Группа Лоренца названа в честь голландского физика Хендрика Лоренца .

Например, следующие законы, уравнения и теории соблюдают симметрию Лоренца:

Кинематические законы специальной теории относительности
Уравнения поля Максвелла в теории электромагнетизма
в Уравнение Дирака теории электрона
Стандартная модель физики элементарных частиц

Группа Лоренца выражает фундаментальную симметрию пространства и времени всех известных фундаментальных законов природы . В достаточно небольших областях пространства-времени, где гравитационные отклонения незначительны, физические законы лоренц-инвариантны так же, как и специальная теория относительности.

Основные свойства [ править ]

Группа Лоренца — подгруппа группы Пуанкаре — группы всех изометрий Минковского пространства-времени . Преобразования Лоренца — это, по сути, изометрии, оставляющие начало координат фиксированным. Таким образом, группа Лоренца является подгруппой изотропии относительно начала группы изометрий пространства-времени Минковского. По этой причине группу Лоренца иногда называют однородной группой Лоренца , а группу Пуанкаре иногда называют неоднородной группой Лоренца . Преобразования Лоренца являются примерами линейных преобразований ; общие изометрии пространства-времени Минковского представляют собой аффинные преобразования .

Определение физики [ править ]

Предположим, две системы отсчета $(t, x, y, z)$ и $(t', x', y', z)$ и две точки $P1 инерциальные$ , $P2'$ , группа Лоренца - это набор всех преобразований между две системы отсчета, сохраняющие скорость света , распространяющегося между двумя точками:

c^{2}(\Delta t')^{2}-(\Delta x')^{2}-(\Delta y')^{2}-(\Delta z')^{2}=c^{2}(\Delta t)^{2}-(\Delta x)^{2}-(\Delta y)^{2}-(\Delta z)^{2}

В матричной форме это все линейные преобразования $Λ$ такие, что:

\Lambda ^{\textsf {T}}\eta \Lambda =\eta \qquad \eta =\operatorname {diag} (1,-1,-1,-1)

Тогда они называются преобразованиями Лоренца.

Математическое определение [ править ]

Математически группу Лоренца можно описать как неопределенную ортогональную группу $O(1, 3)$ — матричную группу Ли , сохраняющую квадратичную форму.

(t,x,y,z)\mapsto t^{2}-x^{2}-y^{2}-z^{2}

на $R 4$ (векторное пространство, снабженное этой квадратичной формой, иногда обозначается $R 1,3$ ). Эта квадратичная форма в матричной форме (см. Классическую ортогональную группу ) интерпретируется в физике как метрический тензор пространства-времени Минковского.

Математические свойства [ править ]

Группа Лоренца — шестимерная некомпактная неабелева вещественная группа Ли несвязная , . Четыре связанных компонента не просто соединены . ^[1] Компонент единицы (т. е. компонент, содержащий элемент единицы) группы Лоренца сам по себе является группой и часто называется ограниченной группой Лоренца и обозначается $SO. + (1, 3)$ . Ограниченная группа Лоренца состоит из тех преобразований Лоренца, которые сохраняют как ориентацию пространства, так и направление времени. Ее фундаментальная группа имеет порядок 2, а ее универсальное накрытие, неопределенная спиновая группа $Spin(1, 3)$ , изоморфна как специальной линейной группе $SL(2, C)$ , так и симплектической группе $Sp(2, C)$ . Эти изоморфизмы позволяют группе Лоренца воздействовать на большое количество математических структур, важных для физики, в первую очередь на спиноры . Таким образом, в релятивистской квантовой механике и в квантовой теории поля очень принято называть $SL(2, C)$ группой Лоренца, понимая, что $SO + (1, 3)$ является его конкретным представлением (векторным представлением).

Рекуррентное представление действия группы Лоренца в пространстве Минковского использует бикватернионы , которые образуют композиционную алгебру . Свойство изометрии преобразований Лоренца выполняется в соответствии со свойством композиции. $|pq|=|p|\times |q|$ .

Еще одним свойством группы Лоренца является конформность или сохранение углов. Повышение Лоренца действует посредством гиперболического вращения плоскости пространства-времени, и такие «вращения» сохраняют гиперболический угол — меру быстроты , используемую в теории относительности. Следовательно, группа Лоренца является подгруппой конформной группы пространства-времени .

Обратите внимание, что в этой статье $O (1, 3)$ называется «группой Лоренца», $SO (1, 3)$ — «собственной группой Лоренца», а $SO + (1, 3)$ как «ограниченная группа Лоренца». Многие авторы (особенно в физике) используют название «группа Лоренца» для $SO(1, 3)$ (или иногда даже $SO + (1, 3)$ ), а не $O(1, 3)$ . Читая таких авторов, важно четко понимать, о ком именно они говорят.

Подключенные компоненты [ править ]

Поскольку это группа Ли , группа Лоренца $O(1, 3)$ является группой и также имеет топологическое описание как гладкое многообразие . Как многообразие, оно имеет четыре компонента связности. Интуитивно это означает, что он состоит из четырех топологически разделенных частей.

Четыре связных компонента можно классифицировать по двум свойствам преобразования, которыми обладают их элементы:

Некоторые элементы меняются местами при преобразованиях Лоренца, инвертирующих время, например, времяподобный вектор, указывающий в будущее , будет инвертирован в вектор, указывающий в прошлое.
Некоторые элементы имеют обратную ориентацию в результате несобственных преобразований Лоренца , например, некоторые Вирбена (тетрады).

Преобразования Лоренца, сохраняющие направление времени, называются ортохронный . Подгруппу ортохронных преобразований часто обозначают $O + (1, 3)$ . Те, которые сохраняют ориентацию, называются собственными и как линейные преобразования имеют определитель $+1$ . (Несобственные преобразования Лоренца имеют определитель $-1$ .) Подгруппа собственных преобразований Лоренца обозначается $SO(1, 3)$ .

Подгруппа всех преобразований Лоренца, сохраняющих как ориентацию, так и направление времени, называется собственной ортохронной группой Лоренца или ограниченной группой Лоренца и обозначается $SO. + (1, 3)$ . ^[а]

Набору из четырех компонентов связности можно придать групповую структуру как факторгруппу $O(1, 3)/SO + (1, 3)$ , которая изоморфна четырёхгруппе Клейна . Каждый элемент в $O(1, 3)$ можно записать как полупрямое произведение правильного ортохронного преобразования и элемента дискретной группы.

{1, П, Т, ПТ}

где P и T — операторы четности и обращения времени :

P = диаг(1, -1, -1, -1)

Т = диаг(-1, 1, 1, 1)

.

Таким образом, произвольное преобразование Лоренца можно определить как правильное ортохронное преобразование Лоренца вместе с дополнительными двумя битами информации, которые выбирают один из четырех компонентов связности. Эта картина типична для конечномерных групп Ли.

группа Лоренца Ограниченная

Ограниченная группа Лоренца $SO + (1, 3)$ является единичной компонентой группы Лоренца, а это означает, что она состоит из всех преобразований Лоренца, которые можно соединить с единицей непрерывной кривой, лежащей в группе. Ограниченная группа Лоренца — это связная нормальная подгруппа полной группы Лоренца той же размерности, в данном случае размерности шесть.

Ограниченная группа Лоренца порождается обычными пространственными вращениями и бустами Лоренца (которые представляют собой вращения в гиперболическом пространстве, включающем времяподобное направление ^[2]). Поскольку каждое правильное ортохронное преобразование Лоренца может быть записано как произведение вращения (заданного тремя действительными параметрами ) и повышения (также заданного тремя действительными параметрами), для задания произвольного правильного ортохронного преобразования Лоренца требуется 6 действительных параметров. Это один из способов понять, почему ограниченная группа Лоренца шестимерна. (См. также алгебру Ли группы Лоренца .)

Набор всех вращений образует подгруппу Ли , изоморфную обычной группе вращений $SO(3)$ . Однако совокупность всех повышений не образует подгруппу, поскольку объединение двух повышений, как правило, не приводит к получению еще одного повышения. (Скорее, пара неколлинеарных повышений эквивалентна повышению и вращению, и это относится к вращению Томаса .) Повышение в некотором направлении или вращение вокруг некоторой оси порождает подгруппу с одним параметром .

Поверхности транзитивности [ править ]

Гиперболоид одного листа

Общая коническая поверхность

Гиперболоид из двух листов

Если группа $G$ действует на пространстве $V$ , то поверхность $S \subset V$ является поверхностью транзитивности , если $S$ инвариантна относительно $G$ (т. е. $\forall g \in G, \forall s \in S : gs \in S$ ) и для любых двух точек $s 1, s 2 \in S$ существует $g \in G$ такой, что $gs 1 = s 2$ . По определению группы Лоренца она сохраняет квадратичную форму

Q(x)=x_{0}^{2}-x_{1}^{2}-x_{2}^{2}-x_{3}^{2}.

Поверхности транзитивности ортохронной группы Лоренца $O + (1, 3)$ , $Q (x) = const.$ действуя на плоское пространство-время $R 1,3$ следующие: ^[3]

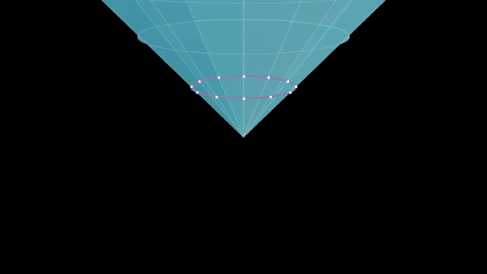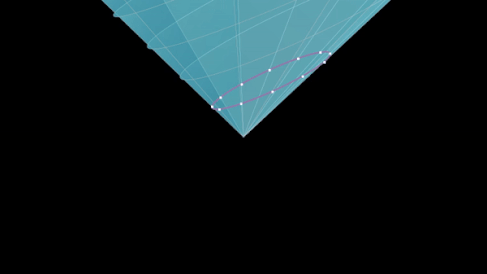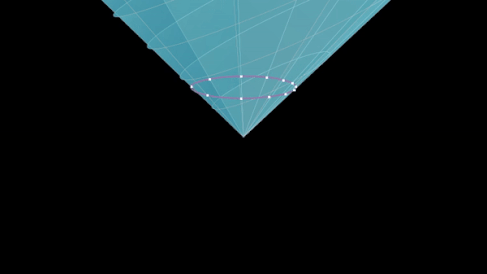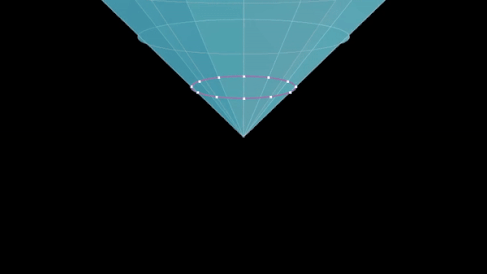
$Q (x) > 0, x 0 > 0$ — верхняя ветвь двухлистного . гиперболоида Точки на этом листе отделены от начала координат будущим времениподобным вектором.
$Q (x) > 0, x 0 < 0$ — нижняя ветвь этого гиперболоида. Точки на этом листе — это времяподобные векторы прошлого.
$Q (x)=0, x0 > 0$ — верхняя ветвь светового конуса , будущий световой конус.
$Q (x) = 0, x 0 < 0$ — нижняя ветвь светового конуса, световой конус прошлого.
$Q (x) < 0$ — однолистный гиперболоид. Точки на этом листе пространственно отделены от начала координат.
Начало координат $x 0 = x 1 = x 2 = x 3 = 0$ .

Эти поверхности $трехмерны$ об , поэтому изображения не точны, но они точны для соответствующих фактов $O. + (1, 2)$ . Для полной группы Лоренца поверхностей транзитивности всего четыре, поскольку преобразование $Т$ переводит верхнюю ветвь гиперболоида (конуса) в нижнюю и наоборот.

Как симметричные пространства [ править ]

Эквивалентный способ сформулировать вышеупомянутые поверхности транзитивности - это симметричное пространство в смысле теории Ли. Например, верхний лист гиперболоида можно записать как факторпространство $SO + (1, 3)/SO(3)$ в силу теоремы о стабилизаторе орбиты . Более того, этот верхний лист также представляет собой модель трехмерного гиперболического пространства .

Представления группы Лоренца [ править ]

Эти наблюдения составляют хорошую отправную точку для нахождения всех бесконечномерных унитарных представлений группы Лоренца, фактически группы Пуанкаре, с использованием метода индуцированных представлений . ^[4]Начинают со «стандартного вектора», по одному для каждой поверхности транзитивности, а затем задаются вопросом, какая подгруппа сохраняет эти векторы. называют малыми группами Эти подгруппы физики . Тогда проблема по существу сводится к более простой проблеме нахождения представлений малых групп. Например, стандартный вектор в одной из гипербол двух листов можно выбрать как $(m, 0, 0, 0)$ . Для каждого $m \neq 0$ вектор пробивает ровно один лист. В этом случае маленькая группа — это $SO(3)$ , группа вращения , все представления которой известны. Точное бесконечномерное унитарное представление, согласно которому преобразуется частица, является частью ее классификации. Не все представления могут соответствовать физическим частицам (насколько известно). Стандартные векторы на однолистных гиперболах соответствовали бы тахионам . Частицы на световом конусе — это фотоны и, более гипотетически, гравитоны . «Частица», соответствующая началу координат, — это вакуум.

Гомоморфизмы и изоморфизмы [ править ]

Несколько других групп либо гомоморфны, либо изоморфны ограниченной группе Лоренца $SO. + (1, 3)$ . Эти гомоморфизмы играют ключевую роль в объяснении различных явлений в физике.

Специальная линейная группа $SL(2, C)$ является двойным накрытием ограниченной группы Лоренца. Это соотношение широко используется для выражения лоренц-инвариантности уравнения Дирака и ковариантности спиноров . Другими словами, (ограниченная) группа Лоренца изоморфна $SL(2, C)/Z 2$
Симплектическая группа $Sp(2, C)$ изоморфна $SL(2, C)$ ; он используется для построения спиноров Вейля , а также для объяснения того, как спиноры могут иметь массу.
Спиновая группа $Spin(1, 3)$ изоморфна $SL(2, C)$ ; она используется для объяснения спина и спиноров в терминах алгебры Клиффорда , что дает понять, как обобщить группу Лоренца на общие положения римановой геометрии , включая теории супергравитации и теорию струн .
Ограниченная группа Лоренца изоморфна проективной специальной линейной группе $PSL(2, C)$ , которая, в свою очередь, изоморфна группе Мёбиуса , группе симметрии конформной геометрии на сфере Римана . Это соотношение является центральным для классификации подгрупп группы Лоренца в соответствии с более ранней схемой классификации, разработанной для группы Мёбиуса.

Представление Вейля [ править ]

Представление Вейля или спинорное отображение — это пара сюръективных гомоморфизмов из $SL(2, C)$ в $SO + (1, 3)$ . Они образуют согласованную пару при преобразованиях четности , соответствующих левому и правому киральным спинорам.

Можно определить действие $SL(2, C)$ на пространство-время Минковского, записав точку пространства-времени в виде эрмитовой матрицы два на два в виде

{\overline {X}}={\begin{bmatrix}ct+z&x-iy\\x+iy&ct-z\end{bmatrix}}=ct1\!\!1+x\sigma _{x}+y\sigma _{y}+z\sigma _{z}=ct1\!\!1+{\vec {x}}\cdot {\vec {\sigma }}

в терминах матриц Паули .

Это представление, представление Вейля, удовлетворяет

\det \,{\overline {X}}=(ct)^{2}-x^{2}-y^{2}-z^{2}.

Таким образом, пространство эрмитовых матриц (которое является четырехмерным, как вещественное векторное пространство) отождествляется с пространством-временем Минковского таким образом, что определителем эрмитовой матрицы является квадрат длины соответствующего вектора в пространстве-времени Минковского. Элемент $S \in SL(2, C)$ действует в пространстве эрмитовых матриц посредством

{\overline {X}}\mapsto S{\overline {X}}S^{\dagger }~,

где $S^{\dagger }$ является транспонированием S $.$ эрмитовым Это действие сохраняет определитель, и поэтому $SL(2, C)$ действует в пространстве-времени Минковского посредством (линейных) изометрий. Форма вышеизложенного с инвертированной четностью:

X=ct1\!\!1-{\vec {x}}\cdot {\vec {\sigma }}

который преобразуется как

X\mapsto \left(S^{-1}\right)^{\dagger }XS^{-1}

То, что это правильное преобразование, следует из того, что

{\overline {X}}X=\left(c^{2}t^{2}-{\vec {x}}\cdot {\vec {x}}\right)1\!\!1=\left(c^{2}t^{2}-x^{2}-y^{2}-z^{2}\right)1\!\!1

остается инвариантным относительно указанной выше пары преобразований.

Эти отображения сюръективны , и ядром любого отображения является двухэлементная подгруппа $\pm I$ . По первой теореме об изоморфизме факторгруппа $PSL(2, C) = SL(2, C)/{\pm I}$ изоморфна $SO + (1, 3)$ .

Карта четности меняет местами эти два покрытия. Это соответствует эрмитовому сопряжению, являющемуся автоморфизмом $SL(2, C)$ . Эти два различных накрытия соответствуют двум различным киральным действиям группы Лоренца на спинорах . Незачеркнутая форма соответствует правым спинорам, преобразующимся как $\psi _{R}\mapsto S\psi _{R}$ , а подчеркнутая форма соответствует левым спинорам, преобразующимся как $\psi _{L}\mapsto \left(S^{\dagger }\right)^{-1}\psi _{L}$ . ^[б]

Важно отметить, что эта пара покрытий не выдерживает квантования; при квантовании это приводит к своеобразному явлению киральной аномалии . Классические (т. е. неквантованные) симметрии группы Лоренца нарушаются квантованием; это содержание теоремы об индексе Атьи-Зингера .

Условные обозначения [ править ]

принято обозначать $В физике преобразование Лоренца Λ \in SO + (1, 3)$ как ${\Lambda ^{\mu }}_{\nu }$ , показывая таким образом матрицу с пространственно-временными индексами $µ, ν = 0, 1, 2, 3$ . Четырехвектор можно создать из матриц Паули двумя разными способами: как $\sigma ^{\mu }=(I,{\vec {\sigma }})$ и в качестве ${\overline {\sigma }}^{\mu }=\left(I,-{\vec {\sigma }}\right)$ . Эти две формы связаны преобразованием четности . Обратите внимание, что ${\overline {\sigma }}_{\mu }=\sigma ^{\mu }$ .

Учитывая преобразование Лоренца $x^{\mu }\mapsto x^{\prime \mu }={\Lambda ^{\mu }}_{\nu }x^{\nu }$ , заданное выше двойное накрытие ортохронной группы Лоренца $S \in SL(2, C)$ можно записать как

x^{\prime \mu }{\overline {\sigma }}_{\mu }={\overline {\sigma }}_{\mu }{\Lambda ^{\mu }}_{\nu }x^{\nu }=Sx^{\nu }{\overline {\sigma }}_{\nu }S^{\dagger }

Удаление $x^{\mu }$ это принимает форму

{\overline {\sigma }}_{\mu }{\Lambda ^{\mu }}_{\nu }=S{\overline {\sigma }}_{\nu }S^{\dagger }

Сопряженная по четности форма

\sigma _{\mu }{\Lambda ^{\mu }}_{\nu }=\left(S^{-1}\right)^{\dagger }\sigma _{\nu }S^{-1}

Доказательство [ править ]

То, что приведенное выше является правильной формой индексированной записи, не сразу очевидно, отчасти потому, что при работе с индексированной записью довольно легко случайно спутать преобразование Лоренца с его обратным или транспонированным. Эта путаница возникает из-за тождества $\eta \Lambda ^{\textsf {T}}\eta =\Lambda ^{-1}$ их трудно распознать, если они написаны в индексированной форме. Преобразования Лоренца не являются тензорами относительно преобразований Лоренца! Таким образом, прямое доказательство этого тождества полезно для установления его правильности. Это можно продемонстрировать, начав с тождества

\omega \sigma ^{k}\omega ^{-1}=-\left(\sigma ^{k}\right)^{\textsf {T}}=-\left(\sigma ^{k}\right)^{*}

где $k=1,2,3$ так что вышеизложенное представляет собой обычные матрицы Паули, и $(\cdot )^{\textsf {T}}$ - транспонирование матрицы, и $(\cdot )^{*}$ является комплексным сопряжением. Матрица $\omega$ является

\omega =i\sigma _{2}={\begin{bmatrix}0&1\\-1&0\end{bmatrix}}

Записанная в виде четырехвектора, связь такова:

\sigma _{\mu }^{\textsf {T}}=\sigma _{\mu }^{*}=\omega {\overline {\sigma }}_{\mu }\omega ^{-1}

Это преобразуется как

{\begin{aligned}\sigma _{\mu }^{\textsf {T}}{\Lambda ^{\mu }}_{\nu }&=\omega {\overline {\sigma }}_{\mu }\omega ^{-1}{\Lambda ^{\mu }}_{\nu }\\&=\omega S\;{\overline {\sigma }}_{\nu }\,S^{\dagger }\omega ^{-1}\\&=\left(\omega S\omega ^{-1}\right)\,\left(\omega {\overline {\sigma }}_{\nu }\omega ^{-1}\right)\,\left(\omega S^{\dagger }\omega ^{-1}\right)\\&=\left(S^{-1}\right)^{\textsf {T}}\,\sigma _{\nu }^{\textsf {T}}\,\left(S^{-1}\right)^{*}\end{aligned}}

Сделав еще одну транспозицию, получим

\sigma _{\mu }{\Lambda ^{\mu }}_{\nu }=\left(S^{-1}\right)^{\dagger }\sigma _{\nu }S^{-1}

Симплектическая группа [ править ]

Симплектическая группа $Sp(2, C)$ изоморфна $SL(2, C)$ . Этот изоморфизм построен так, чтобы сохранить симплектическую билинейную форму на $C 2$ , то есть оставить форму инвариантной относительно преобразований Лоренца. Это можно сформулировать следующим образом. Симплектическая группа определяется как

\operatorname {Sp} (2,\mathbf {C} )=\left\{S\in \operatorname {GL} (2,\mathbf {C} ):S^{\textsf {T}}\omega S=\omega \right\}

где

\omega =i\sigma _{2}={\begin{bmatrix}0&1\\-1&0\end{bmatrix}}

Другие распространенные обозначения: $\omega =\epsilon$ для этого элемента; иногда $используется J$ , но это приводит к путанице с идеей почти сложных структур , которые не одинаковы, поскольку трансформируются по-разному.

Дана пара спиноров Вейля (двухкомпонентных спиноров).

u={\begin{bmatrix}u_{1}\\u_{2}\end{bmatrix}}~,\quad v={\begin{bmatrix}v_{1}\\v_{2}\end{bmatrix}}

инвариантная билинейная форма условно записывается как

\langle u,v\rangle =-\langle v,u\rangle =u_{1}v_{2}-u_{2}v_{1}=u^{\textsf {T}}\omega v

Эта форма инвариантна относительно группы Лоренца, так что для $S \in SL(2, C)$ имеем

\langle Su,Sv\rangle =\langle u,v\rangle

Это определяет своего рода «скалярное произведение» спиноров и обычно используется для определения лоренц-инвариантного массового члена в лагранжианах . Следует отметить несколько примечательных свойств, важных для физики. Во-первых, это $\omega ^{2}=-1$ и так $\omega ^{-1}=\omega ^{\textsf {T}}=\omega ^{\dagger }=-\omega$

Определяющее соотношение можно записать как

\omega S^{\textsf {T}}\omega ^{-1}=S^{-1}

что очень похоже на определяющее соотношение для группы Лоренца

\eta \Lambda ^{\textsf {T}}\eta ^{-1}=\Lambda ^{-1}

где $\eta =\operatorname {diag} (+1,-1,-1,-1)$ — метрический тензор пространства Минковского и, конечно же, $\Lambda \in \operatorname {SO} (1,3)$ как прежде.

покрытия Группы

Поскольку $SL(2, C)$ односвязна, она является универсальной накрывающей ограниченной группы Лоренца $SO + (1, 3)$ . По ограничению существует гомоморфизм $SU(2) \to SO(3)$ . Здесь специальная унитарная группа SU(2), которая изоморфна группе единичной нормы кватернионов , также односвязна, поэтому она является накрывающей группой группы вращений $SO(3)$ . Каждое из этих накрывающих отображений является двойным накрытием в том смысле, что каждому элементу фактора сопоставляются ровно два элемента накрывающей группы. Часто говорят, что ограниченная группа Лоренца и группа вращения двусвязны . Это означает, что фундаментальная группа каждой группы изоморфна двухэлементной циклической группе $Z 2$ .

Двойные накрытия характерны для спиновых групп . Действительно, помимо двойных накрытий

Вращаться + (1, 3) = SL(2, C) \to SO + (1, 3)

Спин(3) = SU(2) \to SO(3)

у нас двойное покрытие

Вывод(1, 3) \to О(1, 3)

Спин(1, 3) \to ТАК(1, 3)

Вращаться + (1, 2) = SU(1, 1) \to SO(1, 2)

Эти спинориальные двойные накрытия строятся из алгебр Клиффорда .

Топология [ править ]

Левая и правая группы в двойном накрытии

СУ(2) \to ТАК(3)

являются деформационными ретрактами левой и правой групп соответственно в двойном накрытии

СЛ(2, С) \to ТАК + (1, 3)

.

Но однородное пространство $SO + (1, 3)/SO(3)$ гиперболическому гомеоморфно 3 -пространству $H 3$ , поэтому мы показали ограниченную группу Лоренца как главное расслоение со слоями $SO(3)$ и базой $H 3$ . Поскольку последний гомеоморфен $R 3$ , а $SO(3)$ гомеоморфно трехмерному вещественному проективному пространству $R P 3$ , мы видим, что ограниченная группа Лоренца локально гомеоморфна произведению $R P 3$ с $Р 3$ . Поскольку базовое пространство стягиваемо, его можно расширить до глобального гомеоморфизма. ^{[ нужны разъяснения ]}

Классы сопряженности [ править ]

Поскольку ограниченная группа Лоренца $SO + (1, 3)$ изоморфна группе Мёбиуса $PSL(2, C)$ , ее классы сопряженности также распадаются на пять классов:

Эллиптические преобразования
Гиперболические преобразования
Локсодромные преобразования
Параболические преобразования
Тривиальное идентичности преобразование

В статье о преобразованиях Мёбиуса объясняется, как возникает эта классификация при рассмотрении неподвижных точек преобразований Мёбиуса в их действии на сферу Римана, что соответствует здесь нулевым собственным пространствам ограниченных преобразований Лоренца в их действии на пространство-время Минковского.

Пример каждого типа приведен в подразделах ниже вместе с эффектом создаваемой им однопараметрической подгруппы (например, на внешний вид ночного неба).

Преобразования Мёбиуса — это конформные преобразования сферы Римана (или небесной сферы). Тогда сопряжение с произвольным элементом из $SL(2, C)$ дает следующие примеры произвольных эллиптических, гиперболических, локсодромных и параболических (ограниченных) преобразований Лоренца соответственно. Воздействие на линии тока соответствующих однопараметрических подгрупп заключается в преобразовании наблюдаемой в примерах картины посредством некоторого конформного преобразования. Например, эллиптическое преобразование Лоренца может иметь любые две различные фиксированные точки на небесной сфере, но точки по-прежнему текут по дугам окружностей от одной фиксированной точки к другой. Остальные случаи аналогичны.

Эллиптический [ править ]

Эллиптический элемент $SL(2, C)$ — это

P_{1}={\begin{bmatrix}\exp \left({\frac {i}{2}}\theta \right)&0\\0&\exp \left(-{\frac {i}{2}}\theta \right)\end{bmatrix}}

и имеет неподвижные точки $ξ$ = 0, ∞. Запись действия как $X \mapsto P 1 X P 1 †$ и собирая члены, спинорное отображение преобразует это в (ограниченное) преобразование Лоренца

Q_{1}={\begin{bmatrix}1&0&0&0\\0&\cos(\theta )&\sin(\theta )&0\\0&-\sin(\theta )&\cos(\theta )&0\\0&0&0&1\end{bmatrix}}=\exp \left(\theta {\begin{bmatrix}0&0&0&0\\0&0&1&0\\0&-1&0&0\\0&0&0&0\end{bmatrix}}\right)~.

Затем это преобразование представляет собой вращение вокруг $оси z$ , exp( $iθJ z$ ). Создаваемая им однопараметрическая подгруппа получается путем принятия $θ$ в качестве действительной переменной, угла поворота, вместо постоянной.

Соответствующие непрерывные преобразования небесной сферы (за исключением идентичности) имеют одни и те же две фиксированные точки — Северный и Южный полюса. Преобразования перемещают все остальные точки по кругам широты, так что эта группа обеспечивает непрерывное вращение против часовой стрелки вокруг $оси z$ по мере $увеличения θ$ . , Удвоение углов наблюдаемое на спинорном отображении, является характерной особенностью спинорных двойных накрытий .

Гиперболический [ править ]

Гиперболическим элементом $SL(2, C)$ является

P_{2}={\begin{bmatrix}\exp \left({\frac {\eta }{2}}\right)&0\\0&\exp \left(-{\frac {\eta }{2}}\right)\end{bmatrix}}

и имеет неподвижные точки $ξ$ = 0, ∞. При стереографической проекции сферы Римана на евклидову плоскость эффектом этого преобразования Мёбиуса является расширение от начала координат.

Спинорное отображение преобразует это в преобразование Лоренца.

Q_{2}={\begin{bmatrix}\cosh(\eta )&0&0&\sinh(\eta )\\0&1&0&0\\0&0&1&0\\\sinh(\eta )&0&0&\cosh(\eta )\end{bmatrix}}=\exp \left(\eta {\begin{bmatrix}0&0&0&1\\0&0&0&0\\0&0&0&0\\1&0&0&0\end{bmatrix}}\right)~.

Это преобразование представляет собой ускорение вдоль $оси z$ с быстротой $η$ . Генерируемая ею однопараметрическая подгруппа получается путем принятия $η$ в качестве действительной переменной, а не константы. Соответствующие непрерывные преобразования небесной сферы (кроме тождественного) все имеют одни и те же фиксированные точки (Северный и Южный полюса) и перемещают все остальные точки по долготе от Южного полюса к Северному полюсу.

Локсодромный [ править ]

Локсодромный элемент $SL(2, C)$ — это

P_{3}=P_{2}P_{1}=P_{1}P_{2}={\begin{bmatrix}\exp \left({\frac {1}{2}}(\eta +i\theta )\right)&0\\0&\exp \left(-{\frac {1}{2}}(\eta +i\theta )\right)\end{bmatrix}}

и имеет неподвижные точки $ξ$ = 0, ∞. Спинорное отображение преобразует это в преобразование Лоренца.

Q_{3}=Q_{2}Q_{1}=Q_{1}Q_{2}={\begin{bmatrix}\cosh(\eta )&0&0&\sinh(\eta )\\0&\cos(\theta )&\sin(\theta )&0\\0&-\sin(\theta )&\cos(\theta )&0\\\sinh(\eta )&0&0&\cosh(\eta )\end{bmatrix}}=\exp {\begin{bmatrix}0&0&0&\eta \\0&0&\theta &0\\0&-\theta &0&0\\\eta &0&0&0\end{bmatrix}}~.

Создаваемая при этом однопараметрическая подгруппа получается путем замены $η + i θ$ на любое вещественное кратное этой комплексной константы. (Если $η$ , $θ$ изменяются независимо, то двумерная абелева подгруппа получается $, состоящая из одновременных вращений вокруг оси z$ и ускорений вдоль $оси z$ ; напротив, обсуждаемая здесь одномерная подгруппа состоит из тех элементов этой двумерная подгруппа, такая, что скорость ускорения и угол поворота имеют фиксированное соотношение .)

Все соответствующие непрерывные преобразования небесной сферы (за исключением идентичности) имеют одни и те же две фиксированные точки (Северный и Южный полюса). Они перемещают все остальные точки от Южного полюса к Северному полюсу (или наоборот) по семейству кривых, называемых локсодромами . Каждый локсодром бесконечно часто вращается вокруг каждого полюса.

Параболический [ править ]

Параболический элемент $SL(2, C)$ — это

P_{4}={\begin{bmatrix}1&\alpha \\0&1\end{bmatrix}}

и имеет единственную неподвижную точку $ξ$ = ∞ на сфере Римана. В стереографической проекции он выглядит как обычное перемещение вдоль действительной оси .

Спинорная карта преобразует это в матрицу (представляющую преобразование Лоренца).

{\begin{aligned}Q_{4}&={\begin{bmatrix}1+{\frac {1}{2}}\vert \alpha \vert ^{2}&\operatorname {Re} (\alpha )&-\operatorname {Im} (\alpha )&-{\frac {1}{2}}\vert \alpha \vert ^{2}\\\operatorname {Re} (\alpha )&1&0&-\operatorname {Re} (\alpha )\\-\operatorname {Im} (\alpha )&0&1&\operatorname {Im} (\alpha )\\{\frac {1}{2}}\vert \alpha \vert ^{2}&\operatorname {Re} (\alpha )&-\operatorname {Im} (\alpha )&1-{\frac {1}{2}}\vert \alpha \vert ^{2}\end{bmatrix}}\\[6pt]&=\exp {\begin{bmatrix}0&\operatorname {Re} (\alpha )&-\operatorname {Im} (\alpha )&0\\\operatorname {Re} (\alpha )&0&0&-\operatorname {Re} (\alpha )\\-\operatorname {Im} (\alpha )&0&0&\operatorname {Im} (\alpha )\\0&\operatorname {Re} (\alpha )&-\operatorname {Im} (\alpha )&0\end{bmatrix}}~.\end{aligned}}

Это порождает двухпараметрическую абелеву подгруппу, которая получается, если рассматривать $α$ как комплексную переменную, а не константу. Соответствующие непрерывные преобразования небесной сферы (кроме тождественного преобразования) перемещают точки по семейству окружностей, которые все касаются на Северном полюсе к определенному большому кругу . По этим окружностям движутся все точки, кроме самого Северного полюса.

Параболические преобразования Лоренца часто называют нулевыми вращениями . Поскольку они, вероятно, наименее знакомы из четырех типов нетождественных преобразований Лоренца (эллиптическое, гиперболическое, локсодромное, параболическое), здесь показано, как определить влияние примера параболического преобразования Лоренца на пространство-время Минковского.

Матрица, приведенная выше, дает преобразование

{\begin{bmatrix}t\\x\\y\\z\end{bmatrix}}\rightarrow {\begin{bmatrix}t\\x\\y\\z\end{bmatrix}}+\operatorname {Re} (\alpha )\;{\begin{bmatrix}x\\t-z\\0\\x\end{bmatrix}}-\operatorname {Im} (\alpha )\;{\begin{bmatrix}y\\0\\z-t\\y\end{bmatrix}}+{\frac {\vert \alpha \vert ^{2}}{2}}\;{\begin{bmatrix}t-z\\0\\0\\t-z\end{bmatrix}}.

Теперь, без ограничения общности, выберем $Im(α) = 0$ . Дифференцирование этого преобразования по теперь уже реальному групповому параметру $α$ и оценка при $α = 0$ дает соответствующее векторное поле (линейный дифференциальный оператор первого порядка),

x\,\left(\partial _{t}+\partial _{z}\right)+(t-z)\,\partial _{x}.

Примените это к функции $f (t, x, y, z)$ и потребуйте, чтобы она оставалась инвариантной; т. е. оно уничтожается в результате этого преобразования. Решение полученного линейного уравнения в частных производных первого порядка можно выразить в виде

f(t,x,y,z)=F\left(y,\,t-z,\,t^{2}-x^{2}-z^{2}\right),

где $F$ — произвольная гладкая функция. Аргументы $F$ дают три рациональных инварианта , описывающих, как точки (события) движутся при этом параболическом преобразовании, поскольку сами они не движутся:

y=c_{1},~~~~t-z=c_{2},~~~~t^{2}-x^{2}-z^{2}=c_{3}.

Выбор реальных значений констант в правых частях дает три условия и, таким образом, задает кривую в пространстве-времени Минковского. Эта кривая является орбитой преобразования.

Вид рациональных инвариантов показывает, что эти линии тока (орбиты) имеют простое описание: исключая несущественную координату $,$ каждая орбита представляет собой пересечение нулевой плоскости t $= z + c 2$ с гиперболоидом t $y 2 - х 2 - г 2 = с 3$ . В случае $c$ ₃ = 0 гиперболоид вырождается в световой конус, а орбиты становятся параболами, лежащими в соответствующих нулевых плоскостях.

Конкретная нулевая линия, лежащая на световом конусе, остается неизменной ; это соответствует единственной (двойной) неподвижной точке на сфере Римана, упомянутой выше. Остальные нулевые линии, проходящие через начало координат, «поворачиваются вокруг конуса» в результате преобразования. Следование за движением одной такой нулевой линии по $мере увеличения α$ соответствует движению точки вдоль одной из круговых линий потока на небесной сфере, как описано выше.

Вместо этого выбор $Re(α) = 0$ создаёт аналогичные орбиты, но теперь с поменянными ролями $x$ и $y$ .

Параболические преобразования приводят к калибровочной симметрии безмассовых частиц (таких как фотоны ) со спиральностью | $ч$ | ≥ 1. В приведенном выше явном примере на безмассовую частицу, движущуюся в $направлении z$ , то есть с 4-импульсом $P = (p, 0, 0, p)$ , вообще не влияет $комбинация x$ -boost и $y$ -вращения. $K x - J y$ , определенный ниже, в «малой группе» его движения. Это очевидно из обсуждаемого явного закона преобразования: как любой светоподобный вектор, сам P теперь инвариантен; т. е. все следы или эффекты $α$ исчезли. $c 1 = c 2 = c 3 = 0$ в обсуждаемом частном случае. (Другой аналогичный генератор, $K y + J x$ , а также он и $J z$ составляют вместе небольшую группу светоподобного вектора, изоморфного $E (2)$ .)

Внешний вид ночного неба [ править ]

Этот изоморфизм приводит к тому, что преобразования Мёбиуса сферы Римана представляют собой способ, которым преобразования Лоренца меняют внешний вид ночного неба, как его видит наблюдатель, маневрирующий с релятивистскими скоростями относительно «неподвижных звезд».

Предположим, «неподвижные звезды» живут в пространстве-времени Минковского и моделируются точками небесной сферы. Тогда данной точке на небесной сфере можно сопоставить $ξ = u + iv$ , комплексное число, которое соответствует точке на сфере Римана , и можно отождествить с нулевым вектором ( светоподобным вектором ) в пространстве Минковского.

{\begin{bmatrix}u^{2}+v^{2}+1\\2u\\-2v\\u^{2}+v^{2}-1\end{bmatrix}}

или, в представлении Вейля (спинорном отображении), эрмитова матрица

N=2{\begin{bmatrix}u^{2}+v^{2}&u+iv\\u-iv&1\end{bmatrix}}.

Набор действительных скалярных кратных этого нулевого вектора, называемый нулевой линией, проходящей через начало координат, представляет собой линию взгляда от наблюдателя в определенном месте и времени (произвольное событие, которое мы можем отождествить с началом пространства-времени Минковского) на различные отдаленные точки. объекты, например звезды. Тогда точки небесной сферы (эквивалентно лучам зрения) отождествляются с определенными эрмитовыми матрицами.

двухсферы и различные Проективная геометрия виды

Эта картина ясно возникает на языке проективной геометрии. (Ограниченная) группа Лоренца действует на проективной небесной сфере . Это пространство ненулевых нулевых векторов с $t>0$ при заданном факторе для проективных пространств: $(t,x,y,z)\sim (t',x',y',z')$ если $(t',x',y',z')=(\lambda t,\lambda x,\lambda y,\lambda z)$ для $\lambda >0$ . Это называется небесной сферой, поскольку позволяет нам изменять масштаб временной координаты. $t$ до 1 после действия с использованием преобразования Лоренца, гарантируя, что пространственная часть находится на единичной сфере.

Со стороны Мёбиуса $SL(2, C)$ действует на комплексном проективном пространстве $C P 1$ , которая, как можно показать, диффеоморфна 2-сфере – ее иногда называют сферой Римана . Фактор по проективному пространству приводит к фактору по группе $SL(2, C)$ .

Наконец, эти два можно связать вместе, используя комплексный проективный вектор для построения нулевого вектора. Если $\xi$ это $C P 1$ проективный вектор, его можно тензорировать с помощью его эрмитова сопряжения, чтобы получить $2\times 2$ Эрмитова матрица. Из других мест этой статьи мы знаем, что это пространство матриц можно рассматривать как 4-вектора. Пространство матриц, возникающее в результате превращения каждого проективного вектора в сфере Римана в матрицу, известно как сфера Блоха .

Алгебра лжи [ править ]

Как и в случае с любой группой Ли, полезным способом изучения многих аспектов группы Лоренца является изучение ее алгебры Ли . Поскольку группа Лоренца $SO(1, 3)$ является матричной группой Ли , соответствующая ей алгебра Ли ${\mathfrak {so}}(1,3)$ является матричной алгеброй Ли, которую можно вычислить как ^[5]

{\mathfrak {so}}(1,3)=\left\{4\times 4\,\,\,\mathbf {R} {\text{-valued matrices}}\,X\mid e^{tX}\in \mathrm {SO} (1,3)\,\mathrm {for} \,\mathrm {all} \,t\right\}

.

Если $\eta$ — диагональная матрица с диагональными элементами $(1, -1, -1, -1)$ , то алгебра Ли ${\mathfrak {o}}(1,3)$ состоит из $4\times 4$ матрицы $X$ такой, что ^[6]

\eta X\eta =-X^{\textsf {T}}

.

Явно, ${\mathfrak {so}}(1,3)$ состоит из $4\times 4$ матрицы вида

{\begin{pmatrix}0&a&b&c\\a&0&d&e\\b&-d&0&f\\c&-e&-f&0\end{pmatrix}}

,

где $a,b,c,d,e,f$ являются произвольными действительными числами. Эта алгебра Ли шестимерна. Подалгебра ${\mathfrak {so}}(1,3)$ состоящее из элементов, в которых $a$ , $b$ , и $c$ равный нулю, изоморфен ${\mathfrak {so}}(3)$ .

Полная группа Лоренца $O(1, 3)$ , собственная группа Лоренца $SO(1, 3)$ и собственная ортохронная группа Лоренца $SO + (1, 3)$ (компонента, связанная с единицей) имеют одну и ту же алгебру Ли, которую обычно обозначают ${\mathfrak {so}}(1,3)$ .

Поскольку единичная компонента группы Лоренца изоморфна конечному фактору группы $SL(2, C)$ (см. выше раздел о связи группы Лоренца с группой Мёбиуса), алгебра Ли группы Лоренца изоморфна Алгебра Ли ${\mathfrak {sl}}(2,\mathbf {C} )$ . Как комплексная алгебра Ли ${\mathfrak {sl}}(2,\mathbf {C} )$ трехмерна, но шестимерна, если рассматривать ее как настоящую алгебру Ли.

алгебры Лоренца соотношения Коммутационные

Стандартные базисные матрицы могут быть проиндексированы как $M^{\mu \nu }$ где $\mu ,\nu$ принимать значения в ${0, 1, 2, 3}$ . Они возникают в результате принятия только одного из $a,b,\cdots ,f$ быть единицей, а другие, в свою очередь, равны нулю. Компоненты можно записать как

(M^{\mu \nu })_{\rho \sigma }=\delta ^{\mu }{}_{\rho }\delta ^{\nu }{}_{\sigma }-\delta ^{\nu }{}_{\rho }\delta ^{\mu }{}_{\sigma }

.

Коммутационные отношения

[M^{\mu \nu },M^{\rho \sigma }]=M^{\mu \sigma }\eta ^{\nu \rho }-M^{\nu \sigma }\eta ^{\mu \rho }+M^{\nu \rho }\eta ^{\mu \sigma }-M^{\mu \rho }\eta ^{\nu \sigma }.

Существуют различные возможные варианты использования соглашения. В физике принято включать коэффициент $i$ с базисными элементами, что дает коэффициент $i$ в коммутационных отношениях.

Затем $M^{0i}$ генерировать импульсы и $M^{ij}$ генерировать вращения.

Структурные константы алгебры Лоренца можно прочитать из коммутационных соотношений. Любой набор базисных элементов, удовлетворяющих этим соотношениям, образует представление алгебры Лоренца.

Генераторы бустов и вращений [ править ]

Группу Лоренца можно рассматривать как подгруппу диффеоморфизмов R $группы 4$ и поэтому ее алгебру Ли можно отождествить с векторными полями на $R 4$ . В частности, векторами, порождающими изометрии в пространстве, являются его векторы Киллинга , что обеспечивает удобную альтернативу левоинвариантному векторному полю для вычисления алгебры Ли. Мы можем записать набор из шести генераторов :

Векторные поля на $R 4$ генерируя три вращения $i J$ ,
$-y\partial _{x}+x\partial _{y}\equiv iJ_{z}~,\qquad -z\partial _{y}+y\partial _{z}\equiv iJ_{x}~,\qquad -x\partial _{z}+z\partial _{x}\equiv iJ_{y}~;$
Векторные поля на $R 4$ генерация трех повышений $i K$ ,
$x\partial _{t}+t\partial _{x}\equiv iK_{x}~,\qquad y\partial _{t}+t\partial _{y}\equiv iK_{y}~,\qquad z\partial _{t}+t\partial _{z}\equiv iK_{z}.$

Коэффициент $i$ , по-видимому, гарантирует, что генераторы вращений являются эрмитовыми.

Здесь может быть полезно вкратце напомнить, как получить однопараметрическую группу из векторного поля , записанного в виде линейного оператора в частных производных первого порядка , такого как

{\mathcal {L}}=-y\partial _{x}+x\partial _{y}.

Соответствующая начальная задача (рассмотрим $r=(x,y)$ функция скаляра $\lambda$ и решить $\partial _{\lambda }r={\mathcal {L}}r$ с некоторыми начальными условиями)

{\frac {\partial x}{\partial \lambda }}=-y,\;{\frac {\partial y}{\partial \lambda }}=x,\;x(0)=x_{0},\;y(0)=y_{0}.

Решение можно записать

x(\lambda )=x_{0}\cos(\lambda )-y_{0}\sin(\lambda ),\;y(\lambda )=x_{0}\sin(\lambda )+y_{0}\cos(\lambda )

или

{\begin{bmatrix}t\\x\\y\\z\end{bmatrix}}={\begin{bmatrix}1&0&0&0\\0&\cos(\lambda )&-\sin(\lambda )&0\\0&\sin(\lambda )&\cos(\lambda )&0\\0&0&0&1\end{bmatrix}}{\begin{bmatrix}t_{0}\\x_{0}\\y_{0}\\z_{0}\end{bmatrix}}

где мы легко распознаем однопараметрическую матричную группу вращений $exp(iλJ z)$ вокруг оси z.

Дифференцируя по групповому параметру $λ$ и полагая его $λ = 0$ в этом результате, мы восстанавливаем стандартную матрицу:

iJ_{z}={\begin{bmatrix}0&0&0&0\\0&0&-1&0\\0&1&0&0\\0&0&0&0\end{bmatrix}}~,

что соответствует векторному полю, с которого мы начали. Это иллюстрирует, как переходить между матричными и векторными представлениями элементов алгебры Ли. Экспоненциальное отображение играет эту особую роль не только для группы Лоренца, но и для групп Ли вообще.

Обращая процедуру, описанную в предыдущем разделе, мы видим, что преобразования Мёбиуса, соответствующие нашим шести генераторам, возникают в результате возведения в степень соответственно $η /2$ (для трех повышений) или $iθ /2$ (для трех вращений), умноженных на три матрицы Паули.

\sigma _{1}={\begin{bmatrix}0&1\\1&0\end{bmatrix}},\;\;\sigma _{2}={\begin{bmatrix}0&-i\\i&0\end{bmatrix}},\;\;\sigma _{3}={\begin{bmatrix}1&0\\0&-1\end{bmatrix}}.

Генераторы группы Мёбиуса [ править ]

Другой порождающий набор возникает из-за изоморфизма группе Мёбиуса. В следующей таблице перечислены шесть генераторов, в которых

В первом столбце дан генератор потока под действием Мёбиуса (после стереографической проекции со сферы Римана) в виде вещественного векторного поля на евклидовой плоскости.
Во втором столбце дана соответствующая однопараметрическая подгруппа преобразований Мёбиуса.
В третьем столбце дана соответствующая однопараметрическая подгруппа преобразований Лоренца (образ при нашем гомоморфизме предыдущей однопараметрической подгруппы).
В четвёртом столбце дан соответствующий генератор потока под действием Лоренца как вещественное векторное поле в пространстве-времени Минковского.

Обратите внимание, что генераторы состоят из

Две параболики (нулевые вращения)
Один гиперболический (повышение в $\partial _{z}$ направление)
Три эллиптики (вращения вокруг осей x , y , z соответственно)

Векторное поле на $R 2$	Однопараметрическая подгруппа группы $SL(2, C)$ , представляющие преобразования Мёбиуса	Однопараметрическая подгруппа $SO + (1, 3)$ , представляющие преобразования Лоренца	Векторное поле на $R 1,3$
Параболический
$\partial _{u}\,\!$	${\begin{bmatrix}1&\alpha \\0&1\end{bmatrix}}$	${\begin{bmatrix}1+{\frac {1}{2}}\alpha ^{2}&\alpha &0&-{\frac {1}{2}}\alpha ^{2}\\\alpha &1&0&-\alpha \\0&0&1&0\\{\frac {1}{2}}\alpha ^{2}&\alpha &0&1-{\frac {1}{2}}\alpha ^{2}\end{bmatrix}}$	${\begin{aligned}X_{1}=x&(\partial _{t}+\partial _{z})+{}\\&(t-z)\partial _{x}\end{aligned}}$
$\partial _{v}\,\!$	${\begin{bmatrix}1&i\alpha \\0&1\end{bmatrix}}$	${\begin{bmatrix}1+{\frac {1}{2}}\alpha ^{2}&0&\alpha &-{\frac {1}{2}}\alpha ^{2}\\0&1&0&0\\\alpha &0&1&-\alpha \\{\frac {1}{2}}\alpha ^{2}&0&\alpha &1-{\frac {1}{2}}\alpha ^{2}\end{bmatrix}}$	${\begin{aligned}X_{2}=y&(\partial _{t}+\partial _{z})+{}\\&(t-z)\partial _{y}\end{aligned}}$
гиперболический
${\frac {1}{2}}\left(u\partial _{u}+v\partial _{v}\right)$	${\begin{bmatrix}\exp \left({\frac {\eta }{2}}\right)&0\\0&\exp \left(-{\frac {\eta }{2}}\right)\end{bmatrix}}$	${\begin{bmatrix}\cosh(\eta )&0&0&\sinh(\eta )\\0&1&0&0\\0&0&1&0\\\sinh(\eta )&0&0&\cosh(\eta )\end{bmatrix}}$	$X_{3}=z\partial _{t}+t\partial _{z}\,\!$
Эллиптический
${\frac {1}{2}}\left(-v\partial _{u}+u\partial _{v}\right)$	${\begin{bmatrix}\exp \left({\frac {i\theta }{2}}\right)&0\\0&\exp \left({\frac {-i\theta }{2}}\right)\end{bmatrix}}$	${\begin{bmatrix}1&0&0&0\\0&\cos(\theta )&-\sin(\theta )&0\\0&\sin(\theta )&\cos(\theta )&0\\0&0&0&1\end{bmatrix}}$	$X_{4}=-y\partial _{x}+x\partial _{y}$
${\frac {v^{2}-u^{2}-1}{2}}\partial _{u}-uv\,\partial _{v}$	${\begin{bmatrix}\cos \left({\frac {\theta }{2}}\right)&-\sin \left({\frac {\theta }{2}}\right)\\\sin \left({\frac {\theta }{2}}\right)&\cos \left({\frac {\theta }{2}}\right)\end{bmatrix}}$	${\begin{bmatrix}1&0&0&0\\0&\cos(\theta )&0&\sin(\theta )\\0&0&1&0\\0&-\sin(\theta )&0&\cos(\theta )\end{bmatrix}}$	$X_{5}=-x\partial _{z}+z\partial _{x}$
$uv\,\partial _{u}+{\frac {1-u^{2}+v^{2}}{2}}\partial _{v}$	${\begin{bmatrix}\cos \left({\frac {\theta }{2}}\right)&i\sin \left({\frac {\theta }{2}}\right)\\i\sin \left({\frac {\theta }{2}}\right)&\cos \left({\frac {\theta }{2}}\right)\end{bmatrix}}$	${\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&\cos(\theta )&-\sin(\theta )\\0&0&\sin(\theta )&\cos(\theta )\end{bmatrix}}$	$X_{6}=-z\partial _{y}+y\partial _{z}$

Рабочий пример: вращение вокруг оси Y [ править ]

Начните с

\sigma _{2}={\begin{bmatrix}0&i\\-i&0\end{bmatrix}}.

Экспоненциально:

\exp \left({\frac {i\theta }{2}}\,\sigma _{2}\right)={\begin{bmatrix}\cos \left({\frac {\theta }{2}}\right)&-\sin \left({\frac {\theta }{2}}\right)\\\sin \left({\frac {\theta }{2}}\right)&\cos \left({\frac {\theta }{2}}\right)\end{bmatrix}}.

Этот элемент $SL(2, C)$ представляет однопараметрическую подгруппу (эллиптических) преобразований Мёбиуса:

\xi \mapsto \xi '={\frac {\cos \left({\frac {\theta }{2}}\right)\,\xi -\sin \left({\frac {\theta }{2}}\right)}{\sin \left({\frac {\theta }{2}}\right)\,\xi +\cos \left({\frac {\theta }{2}}\right)}}.

Следующий,

\left.{\frac {d\xi '}{d\theta }}\right|_{\theta =0}=-{\frac {1+\xi ^{2}}{2}}.

Соответствующее векторное поле на $C$ (мыслимое как образ $S 2$ в стереографической проекции)

-{\frac {1+\xi ^{2}}{2}}\,\partial _{\xi }.

Письмо $\xi =u+iv$ , это становится векторным полем на $R 2$

-{\frac {1+u^{2}-v^{2}}{2}}\,\partial _{u}-uv\,\partial _{v}.

Возвращаясь к нашему элементу $SL(2, C)$ и записывая действие $X\mapsto PXP^{\dagger }$ и собрав термы, находим, что изображение под спинорным отображением является элементом $SO + (1, 3)$

{\begin{bmatrix}1&0&0&0\\0&\cos(\theta )&0&\sin(\theta )\\0&0&1&0\\0&-\sin(\theta )&0&\cos(\theta )\end{bmatrix}}.

Дифференцирование по $θ$ при $θ = 0$ дает соответствующее векторное поле на $R 1,3$ ,

z\partial _{x}-x\partial _{z}.\,\!

Очевидно, это генератор вращения против часовой стрелки вокруг $оси y$ .

Подгруппы группы Лоренца [ править ]

Подалгебры алгебры Ли группы Лоренца можно перечислить с точностью до сопряженности, из чего можно перечислить замкнутые подгруппы ограниченной группы Лоренца с точностью до сопряженности. (Подробности см. в книге Холла, цитируемой ниже.) Их можно легко выразить через генераторы $X_{n}$ приведены в таблице выше.

Одномерные подалгебры, конечно, соответствуют четырем классам сопряженности элементов группы Лоренца:

$X_{1}$ генерирует однопараметрическую подалгебру параболик $SO(0, 1)$ ,
$X_{3}$ генерирует однопараметрическую подалгебру повышений $SO(1, 1)$ ,
$X_{4}$ генерирует однопараметрические вращения $SO(2)$ ,
$X_{3}+aX_{4}$ (для любого $a\neq 0$ ) порождает однопараметрическую подалгебру локсодромных преобразований.

(Строго говоря, последнее соответствует бесконечному числу классов, поскольку различные $a$ давать разные занятия.) Двумерные подалгебры:

$X_{1},X_{2}$ сгенерировать абелеву подалгебру, состоящую полностью из параболик,
$X_{1},X_{3}$ порождаем неабелеву подалгебру, изоморфную алгебре Ли аффинной группы $Aff(1)$ ,
$X_{3},X_{4}$ сгенерируйте абелеву подалгебру, состоящую из повышений, вращений и локсодромики, имеющих одну и ту же пару неподвижных точек.

Трехмерные подалгебры используют схему классификации Бьянки :

$X_{1},X_{2},X_{3}$ порождает подалгебру Бьянки V , изоморфную алгебре Ли $Hom(2)$ , группе евклидовых гомотетий ,
$X_{1},X_{2},X_{4}$ порождает подалгебру Бьянки VII ₀ , изоморфную алгебре Ли $E (2)$ , евклидовой группе ,
$X_{1},X_{2},X_{3}+aX_{4}$ , где $a\neq 0$ , сгенерируйте Бьянки VII _{подалгебру} ,
$X_{1},X_{3},X_{5}$ порождает подалгебру Бианки VIII , изоморфную алгебре Ли $SL(2, R)$ — группе изометрий гиперболической плоскости ,
$X_{4},X_{5},X_{6}$ сгенерировать подалгебру Бьянки IX , изоморфную алгебре Ли $SO(3)$ , группы вращения.

Типы Бьянки относятся к классификации трехмерных алгебр Ли итальянского математика Луиджи Бьянки .

Все четырехмерные подалгебры сопряжены

$X_{1},X_{2},X_{3},X_{4}$ сгенерировать подалгебру, изоморфную алгебре Ли $Sim(2)$ , группе евклидовых подобий .

Подалгебры образуют решетку (см. рисунок), и каждая подалгебра порождает возведением в степень замкнутую подгруппу ограниченной группы Ли. Из них все подгруппы группы Лоренца можно построить с точностью до сопряжения умножением на один из элементов четырехгруппы Клейна.

Как и любая связная группа Ли, смежные классы замкнутых подгрупп ограниченной группы Лоренца или однородные пространства представляют значительный математический интерес. Несколько кратких описаний:

Группа $Sim(2)$ является стабилизатором нулевой линии ; т. е. точки на сфере Римана, поэтому однородное пространство $SO + (1, 3) / Sim(2)$ — это клейнианская геометрия , представляющая конформную геометрию на сфере $S 2$ .
(Единичный компонент) евклидовой группы $SE(2)$ является стабилизатором нулевого вектора , поэтому однородное пространство $SO + (1, 3)/SE(2)$ – импульсное пространство безмассовой частицы; геометрически эта клейнианская геометрия представляет собой вырожденную геометрию светового конуса в пространстве-времени Минковского.
Группа вращений $SO(3)$ является стабилизатором времениподобного вектора , поэтому однородное пространство $SO + (1, 3)/SO(3)$ — пространство импульсов массивной частицы; геометрически это пространство есть не что иное, как трёхмерное гиперболическое пространство $H 3$ .

Обобщение на более высокие измерения [ править ]

Понятие группы Лоренца имеет естественное обобщение на пространство-время любого числа измерений. Математически группа Лоренца ( n + 1)-мерного пространства Минковского представляет собой неопределенную ортогональную группу $O(n, 1)$ линейных преобразований $R п +1$ сохраняющий квадратичную форму

(x_{1},x_{2},\ldots ,x_{n},x_{n+1})\mapsto x_{1}^{2}+x_{2}^{2}+\cdots +x_{n}^{2}-x_{n+1}^{2}.

Группа $O(1, n)$ сохраняет квадратичную форму

(x_{1},x_{2},\ldots ,x_{n},x_{n+1})\mapsto x_{1}^{2}-x_{2}^{2}-\cdots -x_{n+1}^{2}

$O(1, n)$ изоморфен $O(n, 1)$ , и оба представления группы Лоренца используются в сообществе теоретической физики. Первое чаще встречается в литературе, посвященной гравитации, а второе – в литературе по физике элементарных частиц.

Общее обозначение векторного пространства $R п +1$ , оснащенный этим выбором квадратичной формы, равен $R 1, н$ .

Многие свойства группы Лоренца в четырех измерениях (где n = 3 ) напрямую обобщаются на произвольное $n$ . Например, группа Лоренца $O(n, 1)$ имеет четыре компонента связности и действует посредством конформных преобразований на небесной $(n - 1)$ -сфере в $(n + 1)$ -мерном пространстве Минковского. Компонент идентификации $SO + (n, 1)$ является $SO(n)$ -расслоением над гиперболическим $n$ -пространством $H н$ .

Маломерные случаи $n = 1$ и $n = 2$ часто используются в качестве «игрушечных моделей» для физического случая $n = 3$ , тогда как группы Лоренца более высокой размерности используются в физических теориях, таких как теория струн , которые постулируют существование скрытых измерений. . Группа Лоренца $O(n, 1)$ также является группой изометрий $n$ -мерного пространства де Ситтера $dS n$ , которое может быть реализовано как однородное пространство $O(n, 1)/O(n - 1, 1)$ . В частности, $O(4, 1)$ — это группа изометрии вселенной де Ситтера $dS 4$ , космологическая модель.

См. также [ править ]

Примечания [ править ]

^ Обратите внимание, что некоторые авторы ссылаются на $SO(1, 3)$ или даже $O(1, 3)$ , когда они имеют в виду $SO. + (1, 3)$ .
^ См. статью «Уравнение Вейля» для явного вывода.

Ссылки [ править ]

^ Вайнберг 2002
^ Варичак В. 1910 «Теория относительности и геометрия Лобачевского», Phys Z 1910 §3 «Преобразование Лоренца-Эйнштейна как перевод». Engl.tr в Википедии
^ Гельфанд, Минлос и Шапиро 1963.
^ Вигнер 1939 г.
^ Холл, 2015 г. Определение 3.18.
^ Зал 2015 г., Предложение 3.25.

Список чтения [ править ]

Эмиль Артин (1957) Геометрическая алгебра , глава III: Симплектическая и ортогональная геометрия через Интернет-архив , охватывает ортогональные группы $O(p, q)$
Кармели, Моше (1977). Теория групп и общая теория относительности, представления группы Лоренца и их приложения к гравитационному полю . МакГроу-Хилл, Нью-Йорк. ISBN 978-0-07-009986-9 . Каноническая ссылка; см. в главах 1–6. представления группы Лоренца
Франкель, Теодор (2004). Геометрия физики (2-е изд.) . Кембридж: Издательство Кембриджского университета. ISBN 978-0-521-53927-2 . Отличный ресурс по теории Ли, расслоениям, спинорным покрытиям и многим другим темам.
Фултон, Уильям ; Харрис, Джо (1991). Теория представлений. Первый курс . Тексты для аспирантов по математике , Чтения по математике. Том. 129. Нью-Йорк: Springer-Verlag. дои : 10.1007/978-1-4612-0979-9 . ISBN 978-0-387-97495-8 . МР 1153249 . OCLC 246650103 . См. лекцию 11 о неприводимых представлениях $SL(2, C)$ .
Гельфанд, ИМ ; Минлос, РА ; Шапиро, З.Я. (1963), Представления групп вращения и Лоренца и их приложения , Нью-Йорк: Pergamon Press.
Холл, Брайан К. (2015), Группы Ли, алгебры Ли и представления: элементарное введение , Тексты для аспирантов по математике, том. 222 (2-е изд.), Спрингер, ISBN 978-3319134666
Холл, GS (2004). Симметрии и структура кривизны в общей теории относительности . Сингапур: World Scientific. ISBN 978-981-02-1051-9 . См. главу 6 о подалгебрах алгебры Ли группы Лоренца.
Хэтчер, Аллен (2002). Алгебраическая топология . Кембридж: Издательство Кембриджского университета. ISBN 978-0-521-79540-1 . . также См «онлайн-версия» . Проверено 3 июля 2005 г. См. раздел 1.3 , где прекрасно иллюстрировано обсуждение покрытия пространств. См. раздел 3D для топологии групп вращения.
Миснер, Чарльз ; Торн, Кип С .; Уиллер, Джон (1973). Гравитация . WH Фриман и компания . ISBN 978-0-7167-0344-0 . §41.3
Набер, Грегори (1992). Геометрия пространства-времени Минковского . Нью-Йорк: Springer-Verlag. ISBN 978-0486432359 . (Дуврское переиздание.) Отличный справочник по пространству-времени Минковского и группе Лоренца.
Нидхэм, Тристан (1997). Визуальный комплексный анализ . Оксфорд: Издательство Оксфордского университета. ISBN 978-0-19-853446-4 . См. главу 3, где великолепно иллюстрировано обсуждение преобразований Мёбиуса.
Вайнберг, С. (2002), Квантовая теория полей , том. 1, Издательство Кембриджского университета , ISBN 978-0-521-55001-7
Вигнер, EP (1939), «Об унитарных представлениях неоднородной группы Лоренца», Annals of Mathematics , 40 (1): 149–204, Бибкод : 1939AnMat..40..149W , doi : 10.2307/1968551 , JSTOR 1968551 , МР 1503456 , S2CID 121773411

[2] Обратите внимание, что некоторые авторы ссылаются на $SO(1, 3)$ или даже $O(1, 3)$ , когда они имеют в виду $SO. + (1, 3)$ .

[6] См. статью «Уравнение Вейля» для явного вывода.

[1] Вайнберг 2002

[3] Варичак В. 1910 «Теория относительности и геометрия Лобачевского», Phys Z 1910 §3 «Преобразование Лоренца-Эйнштейна как перевод». Engl.tr в Википедии

[Gelfand_1-4] Гельфанд, Минлос и Шапиро 1963.

[5] Вигнер 1939 г.

[7] Холл, 2015 г. Определение 3.18.

[8] Зал 2015 г., Предложение 3.25.

[1]

[а]

[2]

[3]

[4]

[б]

[5]

[6]