Г 2 (математика)

В математике — G ₂ это три простые группы Ли (комплексная форма, компактная действительная форма и расщепленная действительная форма), их алгебры Ли ${\mathfrak {g}}_{2},$ а также некоторые алгебраические группы . Они являются наименьшими из пяти исключительных простых групп Ли . G ₂ имеет ранг 2 и размерность 14. Он имеет два фундаментальных представления с размерностью 7 и 14.

Компактную форму G2 _можно описать как группу автоморфизмов алгебры октонионов или, что то же самое, как подгруппу SO(7), которая сохраняет любой выбранный конкретный вектор в его 8-мерном вещественном спинорном представлении ( спиновое представление ).

История

Алгебра Ли ${\mathfrak {g}}_{2}$, будучи наименьшей исключительной простой алгеброй Ли, была первой из них, обнаруженной при попытке классифицировать простые алгебры Ли. 23 мая 1887 года Вильгельм Киллинг письмо написал Фридриху Энгелю , в котором сообщил, что нашел 14-мерную простую алгебру Ли, которую мы теперь называем ${\mathfrak {g}}_{2}$.

В 1893 году Эли Картан опубликовал заметку с описанием открытого набора в $\mathbb {C} ^{5}$ наделенное двумерным распределением , т. е. плавно меняющимся полем двумерных подпространств касательного пространства, для которого алгебра Ли ${\mathfrak {g}}_{2}$ проявляется как бесконечно малые симметрии. В том же году в том же журнале Энгель заметил то же самое. Позже было обнаружено, что двумерное распределение тесно связано с катанием шарика по другому шарику. Пространство конфигураций катящегося шара пятимерное, с двумерным распределением, описывающим движения шара, при котором он катится без проскальзывания и скручивания.

В 1900 году Энгель обнаружил, что общая антисимметричная трилинейная форма (или 3-форма) в 7-мерном комплексном векторном пространстве сохраняется группой, изоморфной комплексной форме G ₂ .

В 1908 году Картан упомянул, что группа автоморфизмов октонионов представляет собой 14-мерную простую группу Ли. В 1914 году он заявил, что это компактная вещественная форма G ₂ .

В старых книгах и статьях G2 _иногда обозначается _E2 .

Реальные формы

С этой корневой системой связаны три простые вещественные алгебры Ли:

• Основная вещественная алгебра Ли комплексной алгебры Ли G ₂ имеет размерность 28. Она имеет комплексное сопряжение как внешний автоморфизм и односвязна. Максимальная компактная подгруппа ассоциированной с ней группы является компактной формой группы _G2 .
• Алгебра Ли компактной формы 14-мерна. Соответствующая группа Ли не имеет внешних автоморфизмов и центра, является односвязной и компактной.
• Алгебра Ли некомпактной (расщепимой) формы имеет размерность 14. Соответствующая простая группа Ли имеет фундаментальную группу порядка 2, а ее внешняя группа автоморфизмов является тривиальной группой. Его максимальная компактная подгруппа — это SU(2) × SU(2)/(−1,−1) . Он имеет неалгебраическое двойное односвязное покрытие.

Алгебра

Диаграмма Дынкина

Диаграмма Дынкина для G ₂ имеет вид .

Его матрица Картана :

$\left[{\begin{array}{rr}2&-3\\-1&2\end{array}}\right]$

Корни G ₂

12-векторная корневая система G 2 в 2 измерениях.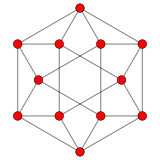

плоскость А 2 Кокстера Проекция 12 вершин кубооктаэдра на содержит такое же двумерное векторное расположение.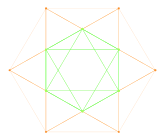

Граф G2 как подгруппы F4 и E8, спроецированный на плоскость Коксетера

Набор простых корней для можно прочитать непосредственно из приведенной выше матрицы Картана. Это (2,−3) и (−1, 2), однако натянутая ими целочисленная решетка не та, что изображена выше (по очевидной причине: шестиугольная решетка на плоскости не может быть порождена целочисленными векторами). Диаграмма выше получена из корней другой пары: $\alpha =\left(1,0\right)$ и ${\textstyle \beta ={\sqrt {3}}\left(\cos {\frac {5\pi }{6}},\sin {\frac {5\pi }{6}}\right)={\frac {1}{2}}\left(-3,{\sqrt {3}}\right)}$. Остальные (положительные) корни — это A = α + β, B = 3α + β, α + A = 2α + β и A + B = 3α + 2β. Хотя они действительно охватывают двумерное пространство, как показано на рисунке, гораздо более симметрично рассматривать их как векторы в двумерном подпространстве трехмерного пространства. В этой идентификации α соответствует e₁-e₂, β - -e₁ + 2e₂-e₃, A - e₂-e₃ и так далее. В евклидовых координатах эти векторы выглядят следующим образом:

(1,−1,0), (−1,1,0) (1,0,−1), (−1,0,1) (0,1,−1), (0,−1,1)

(2,−1,−1), (−2,1,1) (1,−2,1), (−1,2,−1) (1,1,−2), (−1,−1,2)

Соответствующий набор простых корней :

e₁-e₂ = (1,-1,0) и -e₁+2e₂-e₃ = (-1,2,-1)

Примечание: α и A вместе образуют корневую систему, A₂ идентичную , а система, образованная β и B изоморфна A₂ , .

Группа Вейля/Коксетера

Это Вейля / Коксетера. группа $G=W(G_{2})$ это группа диэдра $D_{6}$ порядка 12. Он имеет минимальную точную степень $\mu (G)=5$.

Особая голономия

G2 _группы — одна из возможных специальных групп, которые могут выступать в качестве римановой голономии метрики . Многообразия . голономии G ₂ называют G ₂ -многообразиями также

Полиномиальный инвариант

G ₂ — группа автоморфизмов следующих двух многочленов от 7 некоммутативных переменных.

$C_{1}=t^{2}+u^{2}+v^{2}+w^{2}+x^{2}+y^{2}+z^{2}$

$C_{2}=tuv+wtx+ywu+zyt+vzw+xvy+uxz$ (± перестановки)

который происходит из алгебры октонионов. Переменные должны быть некоммутативными, иначе второй полином будет тождественно нулю.

Генераторы

Добавление представления 14 генераторов с коэффициентами A , ..., N дает матрицу:

$A\lambda _{1}+\cdots +N\lambda _{14}={\begin{bmatrix}0&C&-B&E&-D&-G&F-M\\-C&0&A&F&-G+N&D-K&-E-L\\B&-A&0&-N&M&L&-K\\-E&-F&N&0&-A+H&-B+I&C-J\\D&G-N&-M&A-H&0&J&I\\G&K-D&-L&B-I&-J&0&-H\\-F+M&E+L&K&-C+J&-I&H&0\end{bmatrix}}$

Это в точности алгебра Ли группы

$G_{2}=\{g\in \mathrm {SO} (7):g^{*}\varphi =\varphi ,\varphi =\omega ^{123}+\omega ^{145}+\omega ^{167}+\omega ^{246}-\omega ^{257}-\omega ^{347}-\omega ^{356}\}$

Существует 480 различных представлений $G_{2}$ соответствующие 480 представлениям октонионов. Калиброванная форма, $\varphi$ имеет 30 различных форм и каждая имеет 16 различных знаковых вариаций. Каждая из знаковых вариаций генерирует знаковые различия $G_{2}$ и каждый является автоморфизмом всех 16 соответствующих октонионов. Следовательно, на самом деле существует только 30 различных представлений $G_{2}$. Все это можно построить с помощью алгебры Клиффорда. используя обратимую форму $3e_{1234567}\pm \varphi$ для октонионов. Для других подписанных вариантов $\varphi$, эта форма имеет остатки, которые классифицируют 6 других неассоциативных алгебр, демонстрирующих частичные $G_{2}$ симметрия. Аналогичная калибровка в $\mathrm {Spin} (15)$ приводит к седенионам и как минимум 11 другим родственным алгебрам.

Представления

Вложения максимальных подгрупп группы G ₂ до размерности 77 с соответствующей проекционной матрицей.

Все характеры конечномерных представлений вещественных и комплексных алгебр Ли и групп Ли задаются формулой характеров Вейля . Размеры наименьших неприводимых представлений (последовательность A104599 в OEIS ):

1, 7, 14, 27, 64, 77 (дважды), 182, 189, 273, 286, 378, 448, 714, 729, 748, 896, 924, 1254, 1547, 1728, 1729, 2079 (дважды), 2261, 2926, 3003, 3289, 3542, 4096, 4914, 4928 (дважды), 5005, 5103, 6630, 7293, 7371, 7722, 8372, 9177, 9660, 10206, 10556, 11 571, 11648, 12096, 13090.. ..

14-мерное представление — это присоединенное представление , а 7-мерное — действие G ₂ на мнимые октонионы.

Существуют два неизоморфных неприводимых представления размерностей 77, 2079, 4928, 30107 и т. д. Фундаментальными являются представления размерностей 14 и 7 (соответствующие двум узлам диаграммы Дынкина в таком порядке, что тройная стрелка указывает из первое ко второму).

Воган (1994) описал (бесконечномерные) унитарные неприводимые представления расщепленной вещественной формы G ₂ .

вложения максимальных подгрупп группы G ₂ Справа показаны до размерности 77.

Конечные группы

Группа G2 ₍ q ) это точки алгебраической группы G2 _над конечным полем Fq _— . Эти конечные группы были впервые введены Леонардом Юджином Диксоном в Диксоне (1901) для нечетного q и Диксоне (1905) для четного q . Порядок G ₂ ( q ) равен q ⁶ ( q ⁶ − 1)( q ² − 1) . Когда q ≠ 2 , группа проста , а когда q = 2 , она имеет простую подгруппу индекса 2, изоморфную ² А ₂ (3 ² ), и является группой автоморфизмов максимального порядка октонионов. Группа Янко J ₁ была впервые построена как подгруппа G ₂ (11). Ри (1960) представил скрученные группы Ри . ² G ₂ ( q ) порядка q ³ ( q ³ + 1)( q − 1) для q = 3 ^{2н 1 +} , нечетная степень 3.

См. также

• Матрица Картана
• Диаграмма Дынкина
• Исключительная йордановая алгебра
• Фундаментальное представление
• Г ₂ -структура
• Группа лжи
• Семимерное векторное произведение
• Группа «Простая ложь»
• Звезда Давида

Ссылки

• Адамс, Дж. Франк (1996), Лекции по исключительным группам Ли , Чикагские лекции по математике, University of Chicago Press , ISBN  978-0-226-00526-3 , МР   1428422
• Баэз, Джон (2002), «Октонионы», Bull. амер. Математика. Соц. , 39 (2): 145–205, arXiv : math/0105155 , doi : 10.1090/S0273-0979-01-00934-X , S2CID   586512 .

См. раздел 4.1: G ₂ ; онлайн-версия HTML доступна по адресу http://math.ucr.edu/home/baez/octonions/node14.html .

• Брайант, Роберт (1987), «Метрики с исключительной голономией», Annals of Mathematics , 2, 126 (3): 525–576, doi : 10.2307/1971360 , JSTOR   1971360
• Диксон, Леонард Юджин (1901), «Теория линейных групп в произвольном поле», Труды Американского математического общества , 2 (4), Провиденс, Род-Айленд: Американское математическое общество : 363–394, doi : 10.1090/S0002-9947 -1901-1500573-3 , ISSN   0002-9947 , JSTOR   1986251 , перепечатано в томе II его сборника статей. Леонард Э. Диксон сообщил о группах типа G ₂ в полях нечетной характеристики.
• Диксон, Л. Е. (1905), "Новая система простых групп" , Math. Энн. , 60 : 137–150, doi : 10.1007/BF01447497 , S2CID   179178145 Леонард Э. Диксон сообщил о группах типа G ₂ в полях с четными характеристиками.
• Ри, Римхак (1960), «Семейство простых групп, связанных с простой алгеброй Ли типа (G ₂ )», Бюллетень Американского математического общества , 66 (6): 508–510, doi : 10.1090/S0002-9904 -1960-10523-X , ISSN   0002-9904 , MR   0125155
• Воган, Дэвид А. младший (1994), «Унитарный двойник G ₂ », Inventiones Mathematicae , 116 (1): 677–791, Bibcode : 1994InMat.116..677V , doi : 10.1007/BF01231578 , ISSN   0020- 9910 , МР   1253210 , С2КИД   120845135