Black hole

For other uses, see Black hole (disambiguation).

Direct radio image of a supermassive black hole at the core of Messier 87

Animated simulation of a Schwarzschild black hole with a galaxy passing behind. Around the time of alignment, extreme gravitational lensing of the galaxy is observed.

A black hole is a region of spacetime where gravity is so strong that nothing, not even light and other electromagnetic waves, is capable of possessing enough energy to escape it. Einstein's theory of general relativity predicts that a sufficiently compact mass can deform spacetime to form a black hole. The boundary of no escape is called the event horizon. A black hole has a great effect on the fate and circumstances of an object crossing it, but it has no locally detectable features according to general relativity. In many ways, a black hole acts like an ideal black body, as it reflects no light. Quantum field theory in curved spacetime predicts that event horizons emit Hawking radiation, with the same spectrum as a black body of a temperature inversely proportional to its mass. This temperature is of the order of billionths of a kelvin for stellar black holes, making it essentially impossible to observe directly.

Objects whose gravitational fields are too strong for light to escape were first considered in the 18th century by John Michell and Pierre-Simon Laplace. In 1916, Karl Schwarzschild found the first modern solution of general relativity that would characterize a black hole. David Finkelstein, in 1958, first published the interpretation of "black hole" as a region of space from which nothing can escape. Black holes were long considered a mathematical curiosity; it was not until the 1960s that theoretical work showed they were a generic prediction of general relativity. The discovery of neutron stars by Jocelyn Bell Burnell in 1967 sparked interest in gravitationally collapsed compact objects as a possible astrophysical reality. The first black hole known was Cygnus X-1, identified by several researchers independently in 1971.

Black holes of stellar mass form when massive stars collapse at the end of their life cycle. After a black hole has formed, it can grow by absorbing mass from its surroundings. Supermassive black holes of millions of solar masses (M_☉) may form by absorbing other stars and merging with other black holes, or via direct collapse of gas clouds. There is consensus that supermassive black holes exist in the centres of most galaxies.

The presence of a black hole can be inferred through its interaction with other matter and with electromagnetic radiation such as visible light. Any matter that falls toward a black hole can form an external accretion disk heated by friction, forming quasars, some of the brightest objects in the universe. Stars passing too close to a supermassive black hole can be shredded into streamers that shine very brightly before being "swallowed." If other stars are orbiting a black hole, their orbits can be used to determine the black hole's mass and location. Such observations can be used to exclude possible alternatives such as neutron stars. In this way, astronomers have identified numerous stellar black hole candidates in binary systems and established that the radio source known as Sagittarius A*, at the core of the Milky Way galaxy, contains a supermassive black hole of about 4.3 million solar masses.

History

The idea of a body so big that even light could not escape was briefly proposed by English astronomical pioneer and clergyman John Michell in a letter published in November 1784. Michell's simplistic calculations assumed such a body might have the same density as the Sun, and concluded that one would form when a star's diameter exceeds the Sun's by a factor of 500, and its surface escape velocity exceeds the usual speed of light. Michell correctly noted that such supermassive but non-radiating bodies might be detectable through their gravitational effects on nearby visible bodies. Scholars of the time were initially excited by the proposal that giant but invisible 'dark stars' might be hiding in plain view, but enthusiasm dampened when the wavelike nature of light became apparent in the early nineteenth century, as if light were a wave rather than a particle, it was unclear what, if any, influence gravity would have on escaping light waves.

The modern theory of gravity, general relativity, discredits Michell's notion of a light ray shooting directly from the surface of a supermassive star, being slowed down by the star's gravity, stopping, and then free-falling back to the star's surface. Instead, spacetime itself is curved such that the geodesic that light travels on never leaves the surface of the "star" (black hole).

General relativity

See also: History of general relativity

In 1915, Albert Einstein developed his theory of general relativity, having earlier shown that gravity does influence light's motion. Only a few months later, Karl Schwarzschild found a solution to the Einstein field equations that describes the gravitational field of a point mass and a spherical mass. A few months after Schwarzschild, Johannes Droste, a student of Hendrik Lorentz, independently gave the same solution for the point mass and wrote more extensively about its properties. This solution had a peculiar behaviour at what is now called the Schwarzschild radius, where it became singular, meaning that some of the terms in the Einstein equations became infinite. The nature of this surface was not quite understood at the time.

In 1924, Arthur Eddington showed that the singularity disappeared after a change of coordinates. In 1933, Georges Lemaître realized that this meant the singularity at the Schwarzschild radius was a non-physical coordinate singularity. Arthur Eddington commented on the possibility of a star with mass compressed to the Schwarzschild radius in a 1926 book, noting that Einstein's theory allows us to rule out overly large densities for visible stars like Betelgeuse because "a star of 250 million km radius could not possibly have so high a density as the Sun. Firstly, the force of gravitation would be so great that light would be unable to escape from it, the rays falling back to the star like a stone to the earth. Secondly, the red shift of the spectral lines would be so great that the spectrum would be shifted out of existence. Thirdly, the mass would produce so much curvature of the spacetime metric that space would close up around the star, leaving us outside (i.e., nowhere)."

In 1931, Subrahmanyan Chandrasekhar calculated, using special relativity, that a non-rotating body of electron-degenerate matter above a certain limiting mass (now called the Chandrasekhar limit at 1.4 M_☉) has no stable solutions. His arguments were opposed by many of his contemporaries like Eddington and Lev Landau, who argued that some yet unknown mechanism would stop the collapse. They were partly correct: a white dwarf slightly more massive than the Chandrasekhar limit will collapse into a neutron star, which is itself stable.

In 1939, Robert Oppenheimer and others predicted that neutron stars above another limit, the Tolman–Oppenheimer–Volkoff limit, would collapse further for the reasons presented by Chandrasekhar, and concluded that no law of physics was likely to intervene and stop at least some stars from collapsing to black holes. Their original calculations, based on the Pauli exclusion principle, gave it as 0.7 M_☉. Subsequent consideration of neutron-neutron repulsion mediated by the strong force raised the estimate to approximately 1.5 M_☉ to 3.0 M_☉. Observations of the neutron star merger GW170817, which is thought to have generated a black hole shortly afterward, have refined the TOV limit estimate to ~2.17 M_☉.

Oppenheimer and his co-authors interpreted the singularity at the boundary of the Schwarzschild radius as indicating that this was the boundary of a bubble in which time stopped. This is a valid point of view for external observers, but not for infalling observers. The hypothetical collapsed stars were called "frozen stars", because an outside observer would see the surface of the star frozen in time at the instant where its collapse takes it to the Schwarzschild radius.

Also in 1939, Einstein attempted to prove that black holes were impossible in his publication "On a Stationary System with Spherical Symmetry Consisting of Many Gravitating Masses", using his theory of general relativity to defend his argument. Months later, Oppenheimer and his student Hartland Snyder provided the Oppenheimer–Snyder model in their paper "On Continued Gravitational Contraction", which predicted the existence of black holes. In the paper, which made no reference to Einstein's recent publication, Oppenheimer and Snyder used Einstein's own theory of general relativity to show the conditions on how a black hole could develop, for the first time in contemporary physics.

Golden age

In 1958, David Finkelstein identified the Schwarzschild surface as an event horizon, "a perfect unidirectional membrane: causal influences can cross it in only one direction". This did not strictly contradict Oppenheimer's results, but extended them to include the point of view of infalling observers. Finkelstein's solution extended the Schwarzschild solution for the future of observers falling into a black hole. A complete extension had already been found by Martin Kruskal, who was urged to publish it.

These results came at the beginning of the golden age of general relativity, which was marked by general relativity and black holes becoming mainstream subjects of research. This process was helped by the discovery of pulsars by Jocelyn Bell Burnell in 1967, which, by 1969, were shown to be rapidly rotating neutron stars. Until that time, neutron stars, like black holes, were regarded as just theoretical curiosities; but the discovery of pulsars showed their physical relevance and spurred a further interest in all types of compact objects that might be formed by gravitational collapse.

In this period more general black hole solutions were found. In 1963, Roy Kerr found the exact solution for a rotating black hole. Two years later, Ezra Newman found the axisymmetric solution for a black hole that is both rotating and electrically charged. Through the work of Werner Israel, Brandon Carter, and David Robinson the no-hair theorem emerged, stating that a stationary black hole solution is completely described by the three parameters of the Kerr–Newman metric: mass, angular momentum, and electric charge.

At first, it was suspected that the strange features of the black hole solutions were pathological artifacts from the symmetry conditions imposed, and that the singularities would not appear in generic situations. This view was held in particular by Vladimir Belinsky, Isaak Khalatnikov, and Evgeny Lifshitz, who tried to prove that no singularities appear in generic solutions. However, in the late 1960s Roger Penrose and Stephen Hawking used global techniques to prove that singularities appear generically. For this work, Penrose received half of the 2020 Nobel Prize in Physics, Hawking having died in 2018. Based on observations in Greenwich and Toronto in the early 1970s, Cygnus X-1, a galactic X-ray source discovered in 1964, became the first astronomical object commonly accepted to be a black hole.

Work by James Bardeen, Jacob Bekenstein, Carter, and Hawking in the early 1970s led to the formulation of black hole thermodynamics. These laws describe the behaviour of a black hole in close analogy to the laws of thermodynamics by relating mass to energy, area to entropy, and surface gravity to temperature. The analogy was completed when Hawking, in 1974, showed that quantum field theory implies that black holes should radiate like a black body with a temperature proportional to the surface gravity of the black hole, predicting the effect now known as Hawking radiation.

Observation

On 11 February 2016, the LIGO Scientific Collaboration and the Virgo collaboration announced the first direct detection of gravitational waves, representing the first observation of a black hole merger. On 10 April 2019, the first direct image of a black hole and its vicinity was published, following observations made by the Event Horizon Telescope (EHT) in 2017 of the supermassive black hole in Messier 87's galactic centre. As of 2023, the nearest known body thought to be a black hole, Gaia BH1, is around 1,560 light-years (480 parsecs) away. Though only a couple dozen black holes have been found so far in the Milky Way, there are thought to be hundreds of millions, most of which are solitary and do not cause emission of radiation. Therefore, they would only be detectable by gravitational lensing.

Etymology

John Michell used the term "dark star" in a November 1783 letter to Henry Cavendish, and in the early 20th century, physicists used the term "gravitationally collapsed object". Science writer Marcia Bartusiak traces the term "black hole" to physicist Robert H. Dicke, who in the early 1960s reportedly compared the phenomenon to the Black Hole of Calcutta, notorious as a prison where people entered but never left alive.

The term "black hole" was used in print by Life and Science News magazines in 1963, and by science journalist Ann Ewing in her article "'Black Holes' in Space", dated 18 January 1964, which was a report on a meeting of the American Association for the Advancement of Science held in Cleveland, Ohio.

In December 1967, a student reportedly suggested the phrase "black hole" at a lecture by John Wheeler; Wheeler adopted the term for its brevity and "advertising value", and it quickly caught on, leading some to credit Wheeler with coining the phrase.

Properties and structure

The no-hair theorem postulates that, once it achieves a stable condition after formation, a black hole has only three independent physical properties: mass, electric charge, and angular momentum; the black hole is otherwise featureless. If the conjecture is true, any two black holes that share the same values for these properties, or parameters, are indistinguishable from one another. The degree to which the conjecture is true for real black holes under the laws of modern physics is currently an unsolved problem.

These properties are special because they are visible from outside a black hole. For example, a charged black hole repels other like charges just like any other charged object. Similarly, the total mass inside a sphere containing a black hole can be found by using the gravitational analog of Gauss's law (through the ADM mass), far away from the black hole. Likewise, the angular momentum (or spin) can be measured from far away using frame dragging by the gravitomagnetic field, through for example the Lense–Thirring effect.

An artistic depiction of a black hole and its features

When an object falls into a black hole, any information about the shape of the object or distribution of charge on it is evenly distributed along the horizon of the black hole, and is lost to outside observers. The behavior of the horizon in this situation is a dissipative system that is closely analogous to that of a conductive stretchy membrane with friction and electrical resistance—the membrane paradigm. This is different from other field theories such as electromagnetism, which do not have any friction or resistivity at the microscopic level, because they are time-reversible.

Because a black hole eventually achieves a stable state with only three parameters, there is no way to avoid losing information about the initial conditions: the gravitational and electric fields of a black hole give very little information about what went in. The information that is lost includes every quantity that cannot be measured far away from the black hole horizon, including approximately conserved quantum numbers such as the total baryon number and lepton number. This behavior is so puzzling that it has been called the black hole information loss paradox.

Physical properties

An animation of how light rays can be gravitationally bent

The simplest static black holes have mass but neither electric charge nor angular momentum. These black holes are often referred to as Schwarzschild black holes after Karl Schwarzschild who discovered this solution in 1916. According to Birkhoff's theorem, it is the only vacuum solution that is spherically symmetric. This means there is no observable difference at a distance between the gravitational field of such a black hole and that of any other spherical object of the same mass. The popular notion of a black hole "sucking in everything" in its surroundings is therefore correct only near a black hole's horizon; far away, the external gravitational field is identical to that of any other body of the same mass.

Solutions describing more general black holes also exist. Non-rotating charged black holes are described by the Reissner–Nordström metric, while the Kerr metric describes a non-charged rotating black hole. The most general stationary black hole solution known is the Kerr–Newman metric, which describes a black hole with both charge and angular momentum.

While the mass of a black hole can take any positive value, the charge and angular momentum are constrained by the mass. The total electric charge Q and the total angular momentum J are expected to satisfy the inequality

${\frac {Q^{2}}{4\pi \epsilon _{0}}}+{\frac {c^{2}J^{2}}{GM^{2}}}\leq GM^{2}$

for a black hole of mass M. Black holes with the minimum possible mass satisfying this inequality are called extremal. Solutions of Einstein's equations that violate this inequality exist, but they do not possess an event horizon. These solutions have so-called naked singularities that can be observed from the outside, and hence are deemed unphysical. The cosmic censorship hypothesis rules out the formation of such singularities, when they are created through the gravitational collapse of realistic matter. This is supported by numerical simulations.

Due to the relatively large strength of the electromagnetic force, black holes forming from the collapse of stars are expected to retain the nearly neutral charge of the star. Rotation, however, is expected to be a universal feature of compact astrophysical objects. The black-hole candidate binary X-ray source GRS 1915+105 appears to have an angular momentum near the maximum allowed value. That uncharged limit is

$J\leq {\frac {GM^{2}}{c}},$

allowing definition of a dimensionless spin parameter such that

$0\leq {\frac {cJ}{GM^{2}}}\leq 1.$

Black hole classifications

Class	Approx. mass	Approx. radius
Ultramassive black hole	109–1011 M☉	>1,000 AU
Supermassive black hole	106–109 M☉	0.001–400 AU
Intermediate-mass black hole	102–105 M☉	103 km ≈ REarth
Stellar black hole	2-150 M☉	30 km
Micro black hole	up to MMoon	up to 0.1 mm

Black holes are commonly classified according to their mass, independent of angular momentum, J. The size of a black hole, as determined by the radius of the event horizon, or Schwarzschild radius, is proportional to the mass, M, through

$r_{\mathrm {s} }={\frac {2GM}{c^{2}}}\approx 2.95\,{\frac {M}{M_{\odot }}}~\mathrm {km,}$

where r_s is the Schwarzschild radius and M_☉ is the mass of the Sun. For a black hole with nonzero spin and/or electric charge, the radius is smaller, until an extremal black hole could have an event horizon close to

$r_{\mathrm {+} }={\frac {GM}{c^{2}}}.$

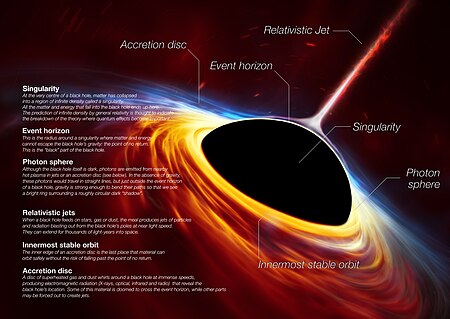
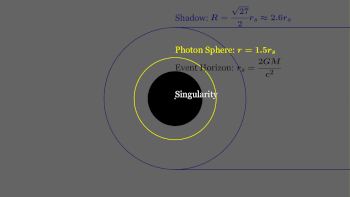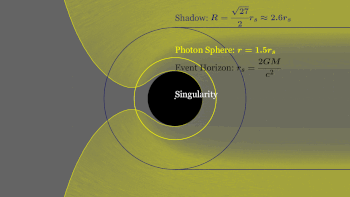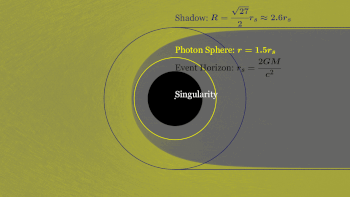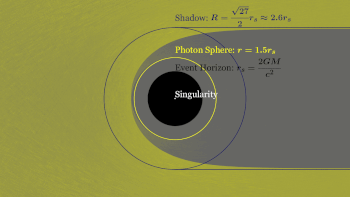
Event horizon

Main article: Event horizon

Far away from the black hole, a particle can move in any direction, as illustrated by the set of arrows. It is restricted only by the speed of light.

Closer to the black hole, spacetime starts to deform. There are more paths going towards the black hole than paths moving away.

Inside of the event horizon, all paths bring the particle closer to the centre of the black hole. It is no longer possible for the particle to escape.

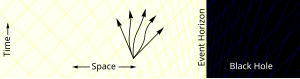
The defining feature of a black hole is the appearance of an event horizon—a boundary in spacetime through which matter and light can pass only inward towards the mass of the black hole. Nothing, not even light, can escape from inside the event horizon. The event horizon is referred to as such because if an event occurs within the boundary, information from that event cannot reach an outside observer, making it impossible to determine whether such an event occurred.

As predicted by general relativity, the presence of a mass deforms spacetime in such a way that the paths taken by particles bend towards the mass. At the event horizon of a black hole, this deformation becomes so strong that there are no paths that lead away from the black hole.

To a distant observer, clocks near a black hole would appear to tick more slowly than those farther away from the black hole. Due to this effect, known as gravitational time dilation, an object falling into a black hole appears to slow as it approaches the event horizon, taking an infinite time to reach it. At the same time, all processes on this object slow down, from the viewpoint of a fixed outside observer, causing any light emitted by the object to appear redder and dimmer, an effect known as gravitational redshift. Eventually, the falling object fades away until it can no longer be seen. Typically this process happens very rapidly with an object disappearing from view within less than a second.

On the other hand, indestructible observers falling into a black hole do not notice any of these effects as they cross the event horizon. According to their own clocks, which appear to them to tick normally, they cross the event horizon after a finite time without noting any singular behaviour; in classical general relativity, it is impossible to determine the location of the event horizon from local observations, due to Einstein's equivalence principle.

The topology of the event horizon of a black hole at equilibrium is always spherical. For non-rotating (static) black holes the geometry of the event horizon is precisely spherical, while for rotating black holes the event horizon is oblate.

Singularity

Main article: Gravitational singularity

At the centre of a black hole, as described by general relativity, may lie a gravitational singularity, a region where the spacetime curvature becomes infinite. For a non-rotating black hole, this region takes the shape of a single point; for a rotating black hole it is smeared out to form a ring singularity that lies in the plane of rotation. In both cases, the singular region has zero volume. It can also be shown that the singular region contains all the mass of the black hole solution. The singular region can thus be thought of as having infinite density.

Observers falling into a Schwarzschild black hole (i.e., non-rotating and not charged) cannot avoid being carried into the singularity once they cross the event horizon. They can prolong the experience by accelerating away to slow their descent, but only up to a limit. When they reach the singularity, they are crushed to infinite density and their mass is added to the total of the black hole. Before that happens, they will have been torn apart by the growing tidal forces in a process sometimes referred to as spaghettification or the "noodle effect".

In the case of a charged (Reissner–Nordström) or rotating (Kerr) black hole, it is possible to avoid the singularity. Extending these solutions as far as possible reveals the hypothetical possibility of exiting the black hole into a different spacetime with the black hole acting as a wormhole. The possibility of traveling to another universe is, however, only theoretical since any perturbation would destroy this possibility. It also appears to be possible to follow closed timelike curves (returning to one's own past) around the Kerr singularity, which leads to problems with causality like the grandfather paradox. It is expected that none of these peculiar effects would survive in a proper quantum treatment of rotating and charged black holes.

The appearance of singularities in general relativity is commonly perceived as signaling the breakdown of the theory. This breakdown, however, is expected; it occurs in a situation where quantum effects should describe these actions, due to the extremely high density and therefore particle interactions. To date, it has not been possible to combine quantum and gravitational effects into a single theory, although there exist attempts to formulate such a theory of quantum gravity. It is generally expected that such a theory will not feature any singularities.

Photon sphere

Main article: Photon sphere

The photon sphere is a spherical boundary where photons that move on tangents to that sphere would be trapped in a non-stable but circular orbit around the black hole.For non-rotating black holes, the photon sphere has a radius 1.5 times the Schwarzschild radius. Their orbits would be dynamically unstable, hence any small perturbation, such as a particle of infalling matter, would cause an instability that would grow over time, either setting the photon on an outward trajectory causing it to escape the black hole, or on an inward spiral where it would eventually cross the event horizon.

While light can still escape from the photon sphere, any light that crosses the photon sphere on an inbound trajectory will be captured by the black hole. Hence any light that reaches an outside observer from the photon sphere must have been emitted by objects between the photon sphere and the event horizon. For a Kerr black hole the radius of the photon sphere depends on the spin parameter and on the details of the photon orbit, which can be prograde (the photon rotates in the same sense of the black hole spin) or retrograde.

Ergosphere

Main article: Ergosphere

The ergosphere is a region outside of the event horizon, where objects cannot remain in place.

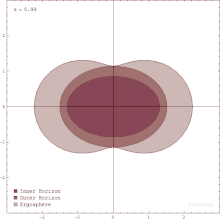
Rotating black holes are surrounded by a region of spacetime in which it is impossible to stand still, called the ergosphere. This is the result of a process known as frame-dragging; general relativity predicts that any rotating mass will tend to slightly "drag" along the spacetime immediately surrounding it. Any object near the rotating mass will tend to start moving in the direction of rotation. For a rotating black hole, this effect is so strong near the event horizon that an object would have to move faster than the speed of light in the opposite direction to just stand still.

The ergosphere of a black hole is a volume bounded by the black hole's event horizon and the ergosurface, which coincides with the event horizon at the poles but is at a much greater distance around the equator.

Objects and radiation can escape normally from the ergosphere. Through the Penrose process, objects can emerge from the ergosphere with more energy than they entered with. The extra energy is taken from the rotational energy of the black hole. Thereby the rotation of the black hole slows down. A variation of the Penrose process in the presence of strong magnetic fields, the Blandford–Znajek process is considered a likely mechanism for the enormous luminosity and relativistic jets of quasars and other active galactic nuclei.

Innermost stable circular orbit (ISCO)

Main article: Innermost stable circular orbit

In Newtonian gravity, test particles can stably orbit at arbitrary distances from a central object. In general relativity, however, there exists an innermost stable circular orbit (often called the ISCO), for which any infinitesimal inward perturbations to a circular orbit will lead to spiraling into the black hole, and any outward perturbations will, depending on the energy, result in spiraling in, stably orbiting between apastron and periastron, or escaping to infinity. The location of the ISCO depends on the spin of the black hole, in the case of a Schwarzschild black hole (spin zero) is:

$r_{\rm {ISCO}}=3\,r_{s}={\frac {6\,GM}{c^{2}}},$

and decreases with increasing black hole spin for particles orbiting in the same direction as the spin.

Plunging region

The final observable region of spacetime around a black hole is called the plunging region. In this area it is no longer possible for matter to follow circular orbits or to stop a final descent into the black hole. Instead it will rapidly plunge toward the black hole close to the speed of light.

Formation and evolution

Given the bizarre character of black holes, it was long questioned whether such objects could actually exist in nature or whether they were merely pathological solutions to Einstein's equations. Einstein himself wrongly thought black holes would not form, because he held that the angular momentum of collapsing particles would stabilize their motion at some radius. This led the general relativity community to dismiss all results to the contrary for many years. However, a minority of relativists continued to contend that black holes were physical objects, and by the end of the 1960s, they had persuaded the majority of researchers in the field that there is no obstacle to the formation of an event horizon.

Penrose demonstrated that once an event horizon forms, general relativity without quantum mechanics requires that a singularity will form within. Shortly afterwards, Hawking showed that many cosmological solutions that describe the Big Bang have singularities without scalar fields or other exotic matter. The Kerr solution, the no-hair theorem, and the laws of black hole thermodynamics showed that the physical properties of black holes were simple and comprehensible, making them respectable subjects for research. Conventional black holes are formed by gravitational collapse of heavy objects such as stars, but they can also in theory be formed by other processes.

Gravitational collapse

Main article: Gravitational collapse

Gas cloud being ripped apart by black hole at the centre of the Milky Way (observations from 2006, 2010 and 2013 are shown in blue, green and red, respectively).

Gravitational collapse occurs when an object's internal pressure is insufficient to resist the object's own gravity. For stars this usually occurs either because a star has too little "fuel" left to maintain its temperature through stellar nucleosynthesis, or because a star that would have been stable receives extra matter in a way that does not raise its core temperature. In either case the star's temperature is no longer high enough to prevent it from collapsing under its own weight.

The collapse may be stopped by the degeneracy pressure of the star's constituents, allowing the condensation of matter into an exotic denser state. The result is one of the various types of compact star. Which type forms depends on the mass of the remnant of the original star left if the outer layers have been blown away (for example, in a Type II supernova). The mass of the remnant, the collapsed object that survives the explosion, can be substantially less than that of the original star. Remnants exceeding 5 M_☉ are produced by stars that were over 20 M_☉ before the collapse.

If the mass of the remnant exceeds about 3–4 M_☉ (the Tolman–Oppenheimer–Volkoff limit), either because the original star was very heavy or because the remnant collected additional mass through accretion of matter, even the degeneracy pressure of neutrons is insufficient to stop the collapse. No known mechanism (except possibly quark degeneracy pressure) is powerful enough to stop the implosion and the object will inevitably collapse to form a black hole.

The gravitational collapse of heavy stars is assumed to be responsible for the formation of stellar mass black holes. Star formation in the early universe may have resulted in very massive stars, which upon their collapse would have produced black holes of up to 10³ M_☉. These black holes could be the seeds of the supermassive black holes found in the centres of most galaxies. It has further been suggested that massive black holes with typical masses of ~10⁵ M_☉ could have formed from the direct collapse of gas clouds in the young universe. These massive objects have been proposed as the seeds that eventually formed the earliest quasars observed already at redshift $z\sim 7$. Some candidates for such objects have been found in observations of the young universe.

While most of the energy released during gravitational collapse is emitted very quickly, an outside observer does not actually see the end of this process. Even though the collapse takes a finite amount of time from the reference frame of infalling matter, a distant observer would see the infalling material slow and halt just above the event horizon, due to gravitational time dilation. Light from the collapsing material takes longer and longer to reach the observer, with the light emitted just before the event horizon forms delayed an infinite amount of time. Thus the external observer never sees the formation of the event horizon; instead, the collapsing material seems to become dimmer and increasingly red-shifted, eventually fading away.

Primordial black holes and the Big Bang

Gravitational collapse requires great density. In the current epoch of the universe these high densities are found only in stars, but in the early universe shortly after the Big Bang densities were much greater, possibly allowing for the creation of black holes. High density alone is not enough to allow black hole formation since a uniform mass distribution will not allow the mass to bunch up. In order for primordial black holes to have formed in such a dense medium, there must have been initial density perturbations that could then grow under their own gravity. Different models for the early universe vary widely in their predictions of the scale of these fluctuations. Various models predict the creation of primordial black holes ranging in size from a Planck mass ($m_{P}={\sqrt {\hbar c/G}}$ ≈ 1.2×10¹⁹ GeV/c² ≈ 2.2×10⁻⁸ kg) to hundreds of thousands of solar masses.

Despite the early universe being extremely dense, it did not re-collapse into a black hole during the Big Bang, since the expansion rate was greater than the attraction. Following inflation theory there was a net repulsive gravitation in the beginning until the end of inflation. Since then the Hubble flow was slowed by the energy density of the universe.

Models for the gravitational collapse of objects of relatively constant size, such as stars, do not necessarily apply in the same way to rapidly expanding space such as the Big Bang.

High-energy collisions

Gravitational collapse is not the only process that could create black holes. In principle, black holes could be formed in high-energy collisions that achieve sufficient density. As of 2002, no such events have been detected, either directly or indirectly as a deficiency of the mass balance in particle accelerator experiments. This suggests that there must be a lower limit for the mass of black holes. Theoretically, this boundary is expected to lie around the Planck mass, where quantum effects are expected to invalidate the predictions of general relativity.

This would put the creation of black holes firmly out of reach of any high-energy process occurring on or near the Earth. However, certain developments in quantum gravity suggest that the minimum black hole mass could be much lower: some braneworld scenarios for example put the boundary as low as 1 TeV/c². This would make it conceivable for micro black holes to be created in the high-energy collisions that occur when cosmic rays hit the Earth's atmosphere, or possibly in the Large Hadron Collider at CERN. These theories are very speculative, and the creation of black holes in these processes is deemed unlikely by many specialists. Even if micro black holes could be formed, it is expected that they would evaporate in about 10⁻²⁵ seconds, posing no threat to the Earth.

Growth

Once a black hole has formed, it can continue to grow by absorbing additional matter. Any black hole will continually absorb gas and interstellar dust from its surroundings. This growth process is one possible way through which some supermassive black holes may have been formed, although the formation of supermassive black holes is still an open field of research. A similar process has been suggested for the formation of intermediate-mass black holes found in globular clusters. Black holes can also merge with other objects such as stars or even other black holes. This is thought to have been important, especially in the early growth of supermassive black holes, which could have formed from the aggregation of many smaller objects. The process has also been proposed as the origin of some intermediate-mass black holes.

Evaporation

Main article: Hawking radiation

In 1974, Hawking predicted that black holes are not entirely black but emit small amounts of thermal radiation at a temperature ℏc³/(8πGMk_B); this effect has become known as Hawking radiation. By applying quantum field theory to a static black hole background, he determined that a black hole should emit particles that display a perfect black body spectrum. Since Hawking's publication, many others have verified the result through various approaches. If Hawking's theory of black hole radiation is correct, then black holes are expected to shrink and evaporate over time as they lose mass by the emission of photons and other particles. The temperature of this thermal spectrum (Hawking temperature) is proportional to the surface gravity of the black hole, which, for a Schwarzschild black hole, is inversely proportional to the mass. Hence, large black holes emit less radiation than small black holes.

A stellar black hole of 1 M_☉ has a Hawking temperature of 62 nanokelvins. This is far less than the 2.7 K temperature of the cosmic microwave background radiation. Stellar-mass or larger black holes receive more mass from the cosmic microwave background than they emit through Hawking radiation and thus will grow instead of shrinking. To have a Hawking temperature larger than 2.7 K (and be able to evaporate), a black hole would need a mass less than the Moon. Such a black hole would have a diameter of less than a tenth of a millimeter.

If a black hole is very small, the radiation effects are expected to become very strong. A black hole with the mass of a car would have a diameter of about 10⁻²⁴ m and take a nanosecond to evaporate, during which time it would briefly have a luminosity of more than 200 times that of the Sun. Lower-mass black holes are expected to evaporate even faster; for example, a black hole of mass 1 TeV/c² would take less than 10⁻⁸⁸ seconds to evaporate completely. For such a small black hole, quantum gravity effects are expected to play an important role and could hypothetically make such a small black hole stable, although current developments in quantum gravity do not indicate this is the case.

The Hawking radiation for an astrophysical black hole is predicted to be very weak and would thus be exceedingly difficult to detect from Earth. A possible exception, however, is the burst of gamma rays emitted in the last stage of the evaporation of primordial black holes. Searches for such flashes have proven unsuccessful and provide stringent limits on the possibility of existence of low mass primordial black holes. NASA's Fermi Gamma-ray Space Telescope launched in 2008 will continue the search for these flashes.

If black holes evaporate via Hawking radiation, a solar mass black hole will evaporate (beginning once the temperature of the cosmic microwave background drops below that of the black hole) over a period of 10⁶⁴ years. A supermassive black hole with a mass of 10¹¹ M_☉ will evaporate in around 2×10¹⁰⁰ years. Some monster black holes in the universe are predicted to continue to grow up to perhaps 10¹⁴ M_☉ during the collapse of superclusters of galaxies. Even these would evaporate over a timescale of up to 10¹⁰⁶ years.

Observational evidence

By nature, black holes do not themselves emit any electromagnetic radiation other than the hypothetical Hawking radiation, so astrophysicists searching for black holes must generally rely on indirect observations. For example, a black hole's existence can sometimes be inferred by observing its gravitational influence on its surroundings.

Direct interferometry

Вид на черную дыру M87* в поляризованном свете.

Стрелец А* , черная дыра в центре Млечного Пути.

Телескоп горизонта событий (EHT) — это активная программа, которая непосредственно наблюдает за ближайшим окружением горизонтов событий черных дыр, таких как черная дыра в центре Млечного Пути. В апреле 2017 года EHT начал наблюдения за черной дырой в центре Мессье 87 . «В целом восемь радиообсерваторий на шести горах и четырех континентах наблюдали галактику в Деве в течение 10 дней в апреле 2017 года», чтобы предоставить данные, дающие изображение в апреле 2019 года.

После двух лет обработки данных EHT опубликовала первое прямое изображение черной дыры. В частности, сверхмассивная черная дыра, лежащая в центре вышеупомянутой галактики. То, что видно, — это не черная дыра, которая выглядит черной из-за потери всего света в этой темной области. Вместо этого именно газы на краю горизонта событий, отображаемые оранжевым или красным цветом, определяют черную дыру.

12 мая 2022 года EHT опубликовала первое изображение Стрельца А* , сверхмассивной черной дыры в центре галактики Млечный Путь . Опубликованное изображение демонстрирует ту же кольцеобразную структуру и круглую тень , что и черная дыра M87* , и изображение было создано с использованием тех же методов, что и для черной дыры M87. Процесс получения изображений Стрельца А*, который более чем в тысячу раз меньше и менее массивен, чем M87*, был значительно сложнее из-за нестабильности его окружения. Изображение Стрельца А* было частично размыто турбулентной плазмой на пути к центру галактики, и этот эффект препятствует разрешению изображения на более длинных волнах.

Считается, что осветление этого материала в «нижней» половине обработанного EHT-изображения вызвано доплеровским излучением , при котором материал, приближающийся к зрителю на релятивистских скоростях, воспринимается как более яркий, чем удаляющийся материал. В случае черной дыры это явление означает, что видимый материал вращается с релятивистской скоростью (>1000 км/с [2200000 миль в час]), единственной скоростью, на которой можно центробежно уравновесить огромное гравитационное притяжение сингулярности. и тем самым оставаться на орбите над горизонтом событий. Такая конфигурация яркого материала подразумевает, что EHT наблюдал M87* с точки зрения, захватывая аккреционный диск черной дыры почти с ребра, поскольку вся система вращалась по часовой стрелке.

Чрезвычайное гравитационное линзирование, связанное с черными дырами, создает иллюзию перспективы, позволяющей увидеть аккреционный диск сверху. На самом деле большая часть кольца на изображении EHT была создана, когда свет, излучаемый дальней стороной аккреционного диска, огибал гравитационный колодец черной дыры и уходил, а это означает, что большинство возможных перспектив на M87 * могут видеть весь диск. , даже то, что прямо за "тенью".

В 2015 году EHT обнаружил магнитные поля недалеко от горизонта событий Стрельца А* и даже распознал некоторые их свойства. Линии поля, проходящие через аккреционный диск, представляли собой сложную смесь упорядоченных и запутанных. Теоретические исследования черных дыр предсказали существование магнитных полей.

В апреле 2023 года было представлено изображение тени черной дыры Мессье 87 и связанного с ней высокоэнергетического джета, впервые наблюдаемое вместе.

Обнаружение гравитационных волн от сливающихся черных дыр

Измерение гравитационных волн с помощью LIGO на детекторах Ливингстона (справа) и Хэнфорда (слева) в сравнении с теоретически предсказанными значениями.

14 сентября 2015 года обсерватория гравитационных волн LIGO провела первое в истории успешное прямое наблюдение гравитационных волн . Сигнал соответствовал теоретическим предсказаниям гравитационных волн, возникающих в результате слияния двух черных дыр: одна с массой около 36 солнечных, а другая с массой около 29 солнечных. Это наблюдение предоставляет наиболее конкретные доказательства существования черных дыр на сегодняшний день. Например, сигнал гравитационной волны предполагает, что расстояние между двумя объектами до слияния составляло всего 350 км, что примерно в четыре раза превышает радиус Шварцшильда, соответствующий предполагаемым массам. Следовательно, объекты должны были быть чрезвычайно компактными, поэтому наиболее правдоподобной интерпретацией остаются черные дыры.

Что еще более важно, сигнал, наблюдаемый LIGO, также включал в себя начало звонка после слияния — сигнала, возникающего, когда вновь сформированный компактный объект переходит в стационарное состояние. Возможно, звонок — это самый прямой способ наблюдения за черной дырой. Из сигнала LIGO можно извлечь частоту и время затухания доминирующего режима звонка. Из них можно сделать вывод о массе и угловом моменте конечного объекта, которые соответствуют независимым предсказаниям численного моделирования слияния. Частота и время затухания доминирующей моды определяются геометрией фотонной сферы. Следовательно, наблюдение этого режима подтверждает наличие фотонной сферы; однако он не может исключить возможные экзотические альтернативы черным дырам, которые достаточно компактны, чтобы иметь фотонную сферу.

Это наблюдение также предоставляет первые наблюдательные доказательства существования двойных черных дыр звездной массы. Кроме того, это первое наблюдательное свидетельство существования черных дыр звездной массы, весящих 25 солнечных масс и более.

еще много гравитационно-волновых событий . С тех пор наблюдалось

Звезды, вращающиеся вокруг Стрельца А*

Основная статья: скопление Стрельца A*

Звезды, движущиеся вокруг Стрельца А*, вид в 2021 году

Собственные движения звезд вблизи центра нашего Млечного Пути предоставляют убедительные наблюдательные доказательства того, что эти звезды вращаются вокруг сверхмассивной черной дыры. С 1995 года астрономы отслеживают движения 90 звезд, вращающихся вокруг невидимого объекта, совпадающего с радиоисточником Стрелец А*. Подгоняя свои движения к кеплеровским орбитам , астрономы в 1998 году смогли сделать вывод, что 2,6 × 10 ⁶  Объект M _☉ должен содержаться в объеме радиусом 0,02 светового года, чтобы вызывать движение этих звезд.

С тех пор одна из звезд, называемая S2 , совершила полный оборот. По орбитальным данным астрономы смогли уточнить расчеты массы до 4,3 × 10 ⁶  M _☉ и радиусом менее 0,002 светового года для объекта, вызывающего орбитальное движение этих звезд. Верхний предел размера объекта все еще слишком велик, чтобы проверить, меньше ли он радиуса Шварцшильда. Тем не менее, эти наблюдения убедительно свидетельствуют о том, что центральным объектом является сверхмассивная черная дыра, поскольку не существует других правдоподобных сценариев удержания такого большого количества невидимой массы в таком маленьком объеме. Кроме того, есть некоторые наблюдательные свидетельства того, что этот объект может обладать горизонтом событий — особенностью, уникальной для черных дыр.

Аккреция материи

См. Также: Аккреционный диск.

Размытие рентгеновских лучей вблизи черной дыры ( NuSTAR ; 12 августа 2014 г.)

Ввиду сохранения углового момента , Газ, попадающий в гравитационную яму, созданную массивным объектом, обычно образует дискообразную структуру вокруг объекта. Впечатления художников, такие как сопутствующее изображение черной дыры с короной, обычно изображают черную дыру так, как если бы это было плоское космическое тело, скрывающее часть диска сразу за ним, но в действительности гравитационное линзирование сильно исказило бы изображение аккреционный диск.

Внутри такого диска трение приведет к переносу углового момента наружу, позволяя веществу упасть дальше внутрь, тем самым высвобождая потенциальную энергию и повышая температуру газа.

Когда аккрецирующим объектом является нейтронная звезда или черная дыра, газ во внутреннем аккреционном диске вращается на очень высоких скоростях из-за его близости к компактному объекту . Возникающее в результате трение настолько велико, что нагревает внутренний диск до температур, при которых он испускает огромное количество электромагнитного излучения (в основном рентгеновских лучей). Эти яркие источники рентгеновского излучения могут быть обнаружены телескопами. Этот процесс аккреции является одним из наиболее эффективных известных процессов производства энергии. До 40% остальной массы аккрецированного материала может излучаться в виде радиации. При ядерном синтезе только около 0,7% остальной массы будет выделено в виде энергии. Во многих случаях аккреционные диски сопровождаются релятивистскими струями , испускающимися вдоль полюсов и уносящими большую часть энергии. Механизм создания этих струй в настоящее время недостаточно изучен, отчасти из-за недостаточности данных.

Таким образом, многие из наиболее энергетических явлений во Вселенной объясняются аккрецией материи на черных дырах. В частности, активные ядра галактик и квазары считаются аккреционными дисками сверхмассивных черных дыр. Аналогичным образом, рентгеновские двойные системы обычно считаются двойными звездными системами, в которых одна из двух звезд представляет собой компактный объект, аккрецирующий вещество от своего компаньона. Было также высказано предположение, что некоторые сверхяркие источники рентгеновского излучения могут быть аккреционными дисками черных дыр промежуточной массы.

Было замечено, что звезды разрываются приливными силами в непосредственной близости от сверхмассивных черных дыр в ядрах галактик, что известно как событие приливного разрушения (TDE) . Часть материала разрушенной звезды образует аккреционный диск вокруг черной дыры, который излучает наблюдаемое электромагнитное излучение.

В ноябре 2011 года было сообщено о первом прямом наблюдении аккреционного диска квазара вокруг сверхмассивной черной дыры.

Рентгеновские двойные системы

Смотрите также: рентгеновский бинарный файл

. рентгеновской обсерваторией Чандра Изображение Лебедя X-1 , первого обнаруженного кандидата в сильные черные дыры, полученное

Рентгеновские двойные системы — это двойные звездные системы, излучающие большую часть своего излучения в рентгеновской части спектра. Обычно считается, что это рентгеновское излучение возникает, когда одна из звезд (компактный объект) аккумулирует вещество другой (обычной) звезды. Наличие в такой системе обычной звезды дает возможность изучить центральный объект и определить, может ли он быть черной дырой.

Если такая система излучает сигналы, которые можно напрямую отследить до компактного объекта, она не может быть черной дырой. Однако отсутствие такого сигнала не исключает возможности того, что компактный объект является нейтронной звездой. Изучая звезду-компаньон, часто можно получить параметры орбиты системы и оценить массу компактного объекта. Если это намного больше предела Толмана-Оппенгеймера-Волкова (максимальная масса, которую звезда может иметь без коллапса), то объект не может быть нейтронной звездой и обычно считается черной дырой.

Первый сильный кандидат на роль черной дыры, Лебедь X-1 , был открыт таким образом Чарльзом Томасом Болтоном . Луиза Вебстер и Пол Мёрдин в 1972 году. Некоторые сомнения оставались из-за неопределенностей, возникающих из-за того, что звезда-компаньон намного тяжелее кандидата в черную дыру. В настоящее время лучшие кандидаты на роль черных дыр находятся в классе рентгеновских двойных систем, называемых мягкими рентгеновскими транзиентами. В этом классе систем звезда-компаньон имеет относительно небольшую массу, что позволяет более точно оценить массу черной дыры. Эти системы активно излучают рентгеновские лучи всего несколько месяцев один раз в 10–50 лет. В период низкого рентгеновского излучения, называемого спокойствием, аккреционный диск чрезвычайно тусклый, что позволяет детально наблюдать звезду-компаньон в этот период. Одним из лучших таких кандидатов является V404 Cygni .

Квазипериодические колебания

Основная статья: Квазипериодические колебания

Рентгеновское излучение аккреционных дисков иногда мерцает на определенных частотах. Эти сигналы называются квазипериодическими колебаниями и, как полагают, вызваны движением материала вдоль внутреннего края аккреционного диска (самая внутренняя стабильная круговая орбита). Таким образом, их частота связана с массой компактного объекта. Таким образом, их можно использовать в качестве альтернативного способа определения массы кандидатов в черные дыры.

Галактические ядра

Смотрите также: Активное ядро ​​галактики.

Обнаружение необычно яркой рентгеновской вспышки от Стрельца А*, черной дыры в центре галактики Млечный Путь , 5   января 2015 г.

Астрономы используют термин «активная галактика» для описания галактик с необычными характеристиками, такими как необычное излучение спектральных линий и очень сильное радиоизлучение. Теоретические и наблюдательные исследования показали, что активность в этих активных ядрах галактик (АЯГ) можно объяснить наличием сверхмассивных черных дыр, которые могут быть в миллионы раз массивнее звездных. Модели этих АЯГ состоят из центральной черной дыры, которая может быть в миллионы или миллиарды раз массивнее Солнца ; диск межзвездного газа и пыли, называемый аккреционным диском; и две струи, перпендикулярные аккреционному диску.

Хотя ожидается, что сверхмассивные черные дыры будут обнаружены в большинстве АЯГ, только ядра некоторых галактик были более тщательно изучены в попытках как идентифицировать, так и измерить фактические массы центральных кандидатов в сверхмассивные черные дыры. Некоторые из наиболее заметных галактик со сверхмассивными кандидатами в черные дыры включают Галактику Андромеды , M32 , M87 , NGC 3115 , NGC 3377 , NGC 4258 , NGC 4889 , NGC 1277 , OJ 287 , APM 08279+5255 и галактику Сомбреро .

Сейчас широко признано, что в центре почти каждой галактики, не только активной, находится сверхмассивная черная дыра. родительской галактики Тесная наблюдательная корреляция между массой этой дыры и дисперсией скоростей балджа , известная как соотношение M-сигма , убедительно свидетельствует о связи между образованием черной дыры и образованием самой галактики.

Микролинзирование

Другой способ проверить природу объекта как черной дыры — это наблюдение эффектов, вызванных сильным гравитационным полем в его окрестностях. Одним из таких эффектов является гравитационное линзирование: деформация пространства-времени вокруг массивного объекта приводит к отклонению световых лучей, например, света, проходящего через оптическую линзу . Были проведены наблюдения за слабой гравитационной линзой, при которой световые лучи отклоняются всего на несколько угловых секунд . Микролинзирование происходит, когда источники неразрешены и наблюдатель видит небольшое просветление. В январе 2022 года астрономы сообщили о первом возможном обнаружении события микролинзирования изолированной черной дыры.

Другой возможностью наблюдения гравитационного линзирования черной дыры было бы наблюдение за звездами, вращающимися вокруг черной дыры. Есть несколько кандидатов на такое наблюдение на орбите Стрельца А* .

Альтернативы

См. также: Экзотическая звезда

Доказательства существования звездных черных дыр во многом основаны на существовании верхнего предела массы нейтронной звезды. Размер этого предела сильно зависит от предположений, сделанных о свойствах плотной материи. Новые экзотические фазы материи могут расширить эту границу. Фаза свободных кварков с высокой плотностью может позволить существование плотных кварковых звезд. а некоторые суперсимметричные модели предсказывают существование Q-звезд . Некоторые расширения стандартной модели постулируют существование преонов как фундаментальных строительных блоков кварков и лептонов , которые гипотетически могут образовывать преонные звезды . Эти гипотетические модели потенциально могли бы объяснить ряд наблюдений звездных кандидатов в черные дыры. Однако из аргументов общей теории относительности можно показать, что любой такой объект будет иметь максимальную массу.

Поскольку средняя плотность черной дыры внутри ее радиуса Шварцшильда обратно пропорциональна квадрату ее массы, сверхмассивные черные дыры гораздо менее плотны, чем звездные черные дыры. Средняя плотность 10 ⁸  Черная дыра M _☉ сравнима с водой. Следовательно, физика материи, образующей сверхмассивную черную дыру, гораздо лучше понята, а возможные альтернативные объяснения наблюдений сверхмассивной черной дыры гораздо более приземлены. Например, сверхмассивную черную дыру можно смоделировать большим скоплением очень темных объектов. Однако такие альтернативы обычно недостаточно стабильны, чтобы объяснить кандидатов в сверхмассивные черные дыры.

Доказательства существования звездных и сверхмассивных черных дыр подразумевают, что для того, чтобы черные дыры не образовались, общая теория относительности должна потерпеть неудачу как теория гравитации, возможно, из-за появления квантово-механических поправок. Долгожданная особенность теории квантовой гравитации заключается в том, что в ней не будет сингулярностей или горизонтов событий, и, следовательно, черные дыры не будут настоящими артефактами. Например, в нечеткого шара модели Согласно теории струн , отдельные состояния решения черной дыры обычно не имеют горизонта событий или сингулярности, но для классического/полуклассического наблюдателя статистическое среднее таких состояний выглядит так же, как обычная черная дыра, как это следует из общей теории относительности.

Было высказано предположение, что несколько теоретических объектов совпадают с наблюдениями за астрономическими кандидатами в черные дыры идентично или почти идентично. но которые функционируют через другой механизм. К ним относятся гравастар , звезда черная , связанный нестар и звезда темной энергии .

Открытые вопросы

Энтропия и термодинамика

Дополнительная информация: Термодинамика черной дыры и граница Бекенштейна.

С = 1 / 4 с ³ к / Для А

Формула энтропии Бекенштейна-Хокинга ( S ) черной дыры, которая зависит от площади черной дыры ( A ). Константы — это скорость света ( c ), постоянная Больцмана ( k ), постоянная Ньютона ( G ) и приведенная постоянная Планка ( ħ ). В планковских единицах это сводится к S = А / 4 .

В 1971 году Хокинг показал в общих условиях что общая площадь горизонтов событий любой группы классических черных дыр никогда не может уменьшиться, даже если они столкнутся и слиться. Этот результат, ныне известный как второй закон механики черных дыр , удивительно похож на второй закон термодинамики , который утверждает, что полная энтропия изолированной системы никогда не может уменьшаться. Как и в случае с классическими объектами при абсолютной нулевой температуре, предполагалось, что черные дыры имеют нулевую энтропию. Если бы это было так, второй закон термодинамики был бы нарушен из-за попадания насыщенной энтропией материи в черную дыру, что привело бы к уменьшению общей энтропии Вселенной. Поэтому Бекенштейн предположил, что энтропия черной дыры должна быть пропорциональна площади ее горизонта.

Связь с законами термодинамики еще больше усилилась после открытия Хокингом в 1974 году того, что квантовая теория поля предсказывает, что черная дыра излучает излучение черного тела при постоянной температуре. По-видимому, это приводит к нарушению второго закона механики черной дыры, поскольку излучение уносит энергию из черной дыры, заставляя ее сжиматься. Излучение уносит также энтропию, и при общих предположениях можно доказать, что сумма энтропии материи, окружающей черную дыру, и четверти площади горизонта, измеренная в планковских единицах, на самом деле всегда увеличивается. Это позволяет сформулировать первый закон механики черных дыр как аналог первого закона термодинамики , где масса действует как энергия, поверхностная гравитация — как температура, а площадь — как энтропия.

Одна загадочная особенность заключается в том, что энтропия черной дыры зависит от ее площади, а не от ее объема, поскольку энтропия обычно представляет собой обширную величину , которая линейно масштабируется с объемом системы. Это странное свойство побудило Джерарда 'т Хоофта и Леонарда Зюскинда предложить голографический принцип , который предполагает, что все, что происходит в пространстве-времени, может быть описано с помощью данных на границе этого объема.

Хотя общую теорию относительности можно использовать для полуклассического расчета энтропии черной дыры, такая ситуация теоретически неудовлетворительна. В статистической механике под энтропией понимают подсчет числа микроскопических конфигураций системы, обладающих одинаковыми макроскопическими качествами, такими как масса, заряд, давление и т. д. Без удовлетворительной теории квантовой гравитации невозможно выполнить такое вычисление для черного цвета. отверстия. Некоторый прогресс был достигнут в различных подходах к квантовой гравитации. В 1995 году Эндрю Стромингер и Камран Вафа показали, что подсчет микросостояний конкретной суперсимметричной черной дыры в теории струн воспроизводит энтропию Бекенштейна – Хокинга. С тех пор аналогичные результаты были получены для различных черных дыр как в теории струн, так и в других подходах к квантовой гравитации, таких как петлевая квантовая гравитация .

Парадокс потери информации

Основная статья: Информационный парадокс черной дыры

Нерешенная задача по физике :

Теряется ли физическая информация в черных дырах?

(еще нерешенные задачи по физике)

Поскольку черная дыра имеет лишь несколько внутренних параметров, большая часть информации о материи, из которой образовалась черная дыра, теряется. Независимо от типа материи, попадающей в черную дыру, оказывается, что сохраняется только информация, касающаяся полной массы, заряда и углового момента. Пока считалось, что черные дыры существуют вечно, эта потеря информации не так уж проблематична, поскольку информацию можно рассматривать как существующую внутри черной дыры, недоступную извне, но представленную на горизонте событий в соответствии с голографическим принципом. Однако черные дыры медленно испаряются, испуская излучение Хокинга. Похоже, что это излучение не несет никакой дополнительной информации о материи, из которой образовалась черная дыра, а это означает, что эта информация, похоже, исчезла навсегда.

Вопрос о том, действительно ли информация теряется в черных дырах ( информационный парадокс черной дыры ), разделил сообщество теоретической физики. В квантовой механике потеря информации соответствует нарушению свойства, называемого унитарностью , и утверждалось, что потеря унитарности также будет означать нарушение закона сохранения энергии. хотя это также оспаривается. За последние годы появились доказательства того, что информация и унитарность действительно сохраняются при полной квантово-гравитационной трактовке проблемы.

Одна из попыток разрешить информационный парадокс черной дыры известна как дополнительность черной дыры . В 2012 году был введен « парадокс межсетевого экрана » с целью продемонстрировать, что дополнительность черных дыр не может решить информационный парадокс. Согласно квантовой теории поля в искривленном пространстве-времени , в одном излучении Хокинга участвуют две взаимно запутанные частицы. Исходящая частица ускользает и испускается как квант излучения Хокинга; падающая частица поглощается черной дырой. Предположим, что черная дыра образовалась в течение конечного времени в прошлом и полностью испарится через какое-то конечное время в будущем. Тогда он будет излучать лишь ограниченное количество информации, закодированной в его излучении Хокинга. Согласно исследованиям таких физиков, как Дон Пейдж и Леонарда Сасскинда, в конечном итоге наступит момент, когда улетающая частица должна будет запутаться со всем излучением Хокинга, которое ранее излучала черная дыра.

По-видимому, это создает парадокс: принцип, называемый « моногамия запутанности », требует, чтобы, как и в любой квантовой системе, выходящая частица не могла быть полностью запутана с двумя другими системами одновременно; однако здесь вылетающая частица кажется запутанной как с падающей частицей, так и независимо с прошлым излучением Хокинга. Чтобы разрешить это противоречие, физики в конечном итоге могут быть вынуждены отказаться от одного из трех проверенных временем принципов: принципа эквивалентности Эйнштейна, унитарности или локальной квантовой теории поля. Одно из возможных решений, которое нарушает принцип эквивалентности, состоит в том, что «брандмауэр» уничтожает входящие частицы на горизонте событий. В целом, от какого из этих предположений следует отказаться (если таковые имеются) остается предметом споров.

См. также

• Двоичная черная дыра
• Черная брана или Черная струна
• Инициатива «Черная дыра»
• Звездолет черной дыры
• Черные дыры в художественной литературе
• Бланет
• БТЗ черная дыра
• Заряженная черная дыра
• Черная дыра с прямым коллапсом
• Золотой бинарный файл
• Гипотетическая черная дыра (значения)
• Кугельблиц (астрофизика)
• Список черных дыр
• Список ближайших черных дыр
• Очертания черных дыр
• Звуковая черная дыра
• Виртуальная черная дыра
• Битва Сасскинд-Хокинг
• Хронология физики черных дыр
• Белая дыра
• Планковская звезда
• Темная звезда (темная материя)
• Радиус Шварцшильда

Дальнейшее чтение

Популярное чтение

• Бегельман, Митчелл; Рис, Мартин (2021). Фатальное притяжение гравитации: черные дыры во Вселенной (Третье изд.). Нью-Йорк: Издательство Кембриджского университета. ISBN  9781108819053 . Архивировано из оригинала 2 января 2022 года . Проверено 6 ноября 2021 г.
• Фергюсон, Китти (1991). Черные дыры в пространстве-времени . Уоттс Франклин. ISBN  978-0-531-12524-3 .
• Хокинг, Стивен (1988). Краткая история времени . Bantam Books, Inc. ISBN  978-0-553-38016-3 .
• Хокинг, Стивен ; Пенроуз, Роджер (1996). Природа пространства и времени . Издательство Принстонского университета. ISBN  978-0-691-03791-2 . Архивировано из оригинала 18 октября 2021 года . Проверено 16 мая 2020 г.
• Левин, Жанна (2020). Руководство по выживанию в черной дыре . Нью-Йорк: Альфред А. Кнопф. ISBN  9780525658221 . Архивировано из оригинала 22 марта 2022 года . Проверено 6 ноября 2021 г.
• Мелия, Фульвио (2003). Черная дыра в центре нашей Галактики . Принстон Ю Пресс. ISBN  978-0-691-09505-9 .
• Мелия, Фульвио (2003). Грань бесконечности. Сверхмассивные черные дыры во Вселенной . Кембриджский университет Пресс. ISBN  978-0-521-81405-8 .
• Пиковер, Клиффорд (1998). Черные дыры: Путеводитель путешественника . Wiley, John & Sons, Inc. ISBN  978-0-471-19704-1 .
• Торн, Кип С. (1994). Черные дыры и искривления времени . Norton, WW & Company, Inc. ISBN  978-0-393-31276-8 .
• Сасскинд, Леонард (2008). Война черных дыр: моя битва со Стивеном Хокингом за то, чтобы сделать мир безопасным для квантовой механики . Литтл, Браун и компания. ISBN  978-0316016407 .
• Уиллер, Дж. Крейг (2007). Космические катастрофы (2-е изд.). Издательство Кембриджского университета. ISBN  978-0-521-85714-7 .

Университетские учебники и монографии

• Кэрролл, Шон М. (2004). Пространство-время и геометрия . Эддисон Уэсли. ISBN  978-0-8053-8732-2 . Конспекты лекций, на которых основана книга, доступны бесплатно на веб-сайте Шона Кэрролла. Архивировано 23 марта 2017 года на Wayback Machine .
• Картер, Б. (1973). «Состояния равновесия черной дыры». В ДеВитте, бакалавр наук ; ДеВитт, К. (ред.). Черные дыры .
• Чандрасекар, Субраманян (1999). Математическая теория черных дыр . Издательство Оксфордского университета. ISBN  978-0-19-850370-5 .
• Фролов Валерий П.; Новиков, Игорь Д. (1998). Физика черных дыр . Фундаментальные теории физики. Том. 96. дои : 10.1007/978-94-011-5139-9 . ISBN  978-0-7923-5146-7 .
• Фролов Валерий П.; Зельников, Андрей (2011). Введение в физику черных дыр . Оксфорд: Издательство Оксфордского университета. ISBN  978-0-19-969229-3 . Збл   1234.83001 . Архивировано из оригинала 22 марта 2022 года . Проверено 2 января 2022 г.
• Хокинг, Юго-Запад ; Эллис, СКФ (1973). Крупномасштабная структура пространства-времени . Издательство Кембриджского университета. ISBN  978-0-521-09906-6 . Архивировано из оригинала 21 июля 2020 года . Проверено 16 мая 2020 г.
• Мелия, Фульвио (2007). Галактическая сверхмассивная черная дыра . Принстон Ю Пресс. ISBN  978-0-691-13129-0 .
• Миснер, Чарльз ; Торн, Кип С .; Уиллер, Джон (1973). Гравитация . WH Фриман и компания. ISBN  978-0-7167-0344-0 .
• Тейлор, Эдвин Ф.; Уилер, Джон Арчибальд (2000). Исследование черных дыр . Эддисон Уэсли Лонгман. ISBN  978-0-201-38423-9 .
• Уолд, Роберт М. (1984). Общая теория относительности . Издательство Чикагского университета. ISBN  978-0-226-87033-5 . Архивировано из оригинала 11 августа 2016 года . Проверено 23 февраля 2016 г.
• Уолд, Роберт М. (1992). Пространство, время и гравитация: теория большого взрыва и черных дыр . Издательство Чикагского университета. ISBN  978-0-226-87029-8 .
• Прайс, Ричард; Крейтон, Тевиет (2008). «Чёрные дыры» . Схоларпедия . 3 (1): 4277. Бибкод : 2008SchpJ...3.4277C . дои : 10.4249/scholarpedia.4277 .

Обзорные статьи

• Хьюз, Скотт А. (2005). «Доверяй, но проверяй: аргументы в пользу астрофизических черных дыр». arXiv : hep-ph/0511217 . Конспекты лекций SLAC 2005 г. Летнего института
• Галло, Елена; Марольф, Дональд (2009). «Ресурсное письмо BH-2: Черные дыры». Американский журнал физики . 77 (4): 294–307. arXiv : 0806.2316 . Бибкод : 2009AmJPh..77..294G . дои : 10.1119/1.3056569 . S2CID   118494056 .
• Кардозо, Витор; Пани, Паоло (2019). «Тестирование природы темных компактных объектов: отчет о состоянии». Живые обзоры в теории относительности . 22 (1): 4. arXiv : 1904.05363 . Бибкод : 2019LRR....22....4C . дои : 10.1007/s41114-019-0020-4 . S2CID   256465740 .
• Манн, Роберт Б.; Мурк, Себастьян; Терно, Дэниел Р. (2022). «Черные дыры и их горизонты в полуклассической и модифицированной теориях гравитации». Международный журнал современной физики Д. 31 (9): 2230015–2230276. arXiv : 2112.06515 . Бибкод : 2022IJMPD..3130015M . дои : 10.1142/S0218271822300154 . S2CID   245123647 .

Внешние ссылки

• Черные дыры в программе «В наше время » на BBC
• Стэнфордская энциклопедия философии : « Сингулярности и черные дыры » Эрика Куриела и Питера Бокулича.
• Черные дыры: неумолимое притяжение гравитации - интерактивный мультимедийный веб-сайт о физике и астрономии черных дыр от Научного института космического телескопа (HubbleSite)
• ЕКА. Архивировано Визуализация черной дыры 3 мая 2019 года на Wayback Machine.
• Часто задаваемые вопросы (FAQ) о черных дырах
• Шварцшильдовская геометрия
• Черные дыры – основные сведения (NYT; апрель 2021 г.)

Видео

• 16-летнее исследование отслеживает звезды, вращающиеся вокруг Стрельца А*
• Фильм о кандидате в чёрную дыру из Института Макса Планка
• Коуэн, Рон (20 апреля 2015 г.). «3D-моделирование сталкивающихся черных дыр признано наиболее реалистичным» . Природа . дои : 10.1038/nature.2015.17360 .
• Компьютерная визуализация сигнала, обнаруженного LIGO
• Две черные дыры сливаются в одну (по сигналу GW150914)