Фотонная сфера

Эта статья о физике фотонов под действием гравитации. Чтобы узнать о части звезды, излучающей свет, см. Фотосфера . Чтобы узнать о псевдонаучных духовных убеждениях, см. Фотонный пояс .

Анимация того, как лучи света можно гравитационно изгибать, образуя фотонную сферу.

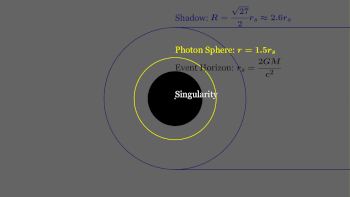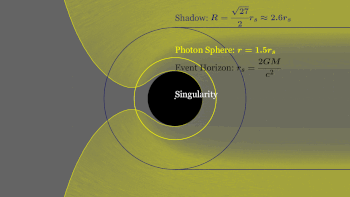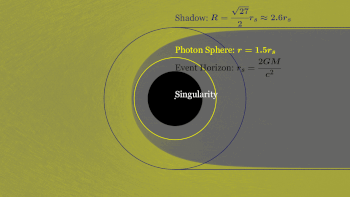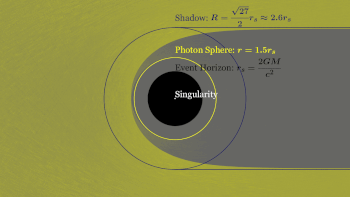
Фотонная сфера или фотонный круг возникает вблизи горизонта событий черной дыры, где гравитация настолько сильна, что испускаемые фотоны не просто огибают черную дыру, но и возвращаются в точку, из которой они были испущены, и, следовательно, проявляют свойства бумеранга. Когда источник, излучающий фотоны, попадает в гравитационное поле по направлению к горизонту событий, форма траектории каждого фотона-бумеранга меняется, стремясь к более круговой форме. При критическом значении радиального расстояния от сингулярности траектория фотона-бумеранга примет форму нестабильной круговой орбиты, образуя фотонный круг и, следовательно, в совокупности фотонную сферу. Круговая орбита фотона называется последней орбитой фотона . Радиус фотонной сферы, который также является нижней границей любой стабильной орбиты , для черной дыры Шварцшильда равен

$r={\frac {3GM}{c^{2}}}={\frac {3r_{\text{s}}}{2}},$

где G — гравитационная постоянная , M — масса черной дыры , c — скорость света в вакууме, а rs _— радиус Шварцшильда (радиус горизонта событий ); см. ниже вывод этого результата.

Из этого уравнения следует, что фотонные сферы могут существовать только в пространстве, окружающем чрезвычайно компактный объект ( черную дыру или, возможно, «сверхкомпактную» нейтронную звезду). ).

Фотонная сфера расположена дальше от центра черной дыры, чем горизонт событий. Внутри фотонной сферы можно представить себе фотон , который испускается (или отражается) из затылка и, следуя по орбите черной дыры, затем перехватывается глазом человека, позволяя увидеть заднюю часть фотонной сферы. голова, см., например Для невращающихся черных дыр фотонная сфера представляет собой сферу радиуса 3/2 r _s . Не существует стабильных орбит свободного падения, существующих внутри фотонной сферы или пересекающих ее. Любая орбита свободного падения, пересекающая его снаружи, превращается в черную дыру. Любая орбита, пересекающая ее изнутри, уходит в бесконечность или падает обратно и по спирали попадает в черную дыру. Никакая неускоренная орбита с большой полуосью меньше этого расстояния невозможна, но внутри фотонной сферы постоянное ускорение позволит космическому кораблю или зонду зависать над горизонтом событий.

Еще одним свойством фотонной сферы является обращение центробежной силы (примечание: не центростремительной ). За пределами фотонной сферы, чем быстрее человек вращается, тем большую внешнюю силу он ощущает. Центробежная сила падает до нуля на фотонной сфере, включая орбиты несвободного падения на любой скорости, т.е. объект весит одинаково, независимо от того, насколько быстро он вращается, и становится отрицательным внутри него. Внутри фотонной сферы более быстрое вращение по орбите приводит к увеличению веса или внутренней силы. Это имеет серьезные последствия для гидродинамики входящего потока жидкости.

Вращающаяся черная дыра имеет две фотонные сферы. Когда черная дыра вращается, она увлекает за собой пространство. Фотонная сфера, которая находится ближе к черной дыре, движется в том же направлении, что и вращение, тогда как фотонная сфера, расположенная дальше, движется против нее. Чем больше угловая скорость вращения черной дыры, тем больше расстояние между двумя фотонными сферами. Поскольку у черной дыры есть ось вращения, это справедливо только при приближении к черной дыре в направлении экватора. На полярной орбите находится только одна фотонная сфера. Это связано с тем, что при приближении под таким углом не существует возможности движения по вращению или против него. Вместо этого вращение вызовет прецессию орбиты .

Дополнительная информация: Фотонная поверхность.

Вывод для черной дыры Шварцшильда

Поскольку черная дыра Шварцшильда обладает сферической симметрией, все возможные оси круговой орбиты фотона эквивалентны, и все круговые орбиты имеют одинаковый радиус.

Этот вывод предполагает использование метрики Шварцшильда , определяемой формулой

$ds^{2}=\left(1-{\frac {r_{\text{s}}}{r}}\right)c^{2}\,dt^{2}-\left(1-{\frac {r_{\text{s}}}{r}}\right)^{-1}\,dr^{2}-r^{2}(\sin ^{2}\theta \,d\phi ^{2}+d\theta ^{2}).$

Для фотона, движущегося с постоянным радиусом r (т.е. в направлении координаты φ ), $dr=0$. Поскольку это фотон, $ds=0$ («светоподобный интервал»). Мы всегда можем повернуть систему координат так, что $\theta$ является постоянным, $d\theta =0$ (например, $\theta =\pi /2$).

Приравняв ds , dr и dθ к нулю, мы имеем

$\left(1-{\frac {r_{\text{s}}}{r}}\right)c^{2}\,dt^{2}=r^{2}\sin ^{2}\theta \,d\phi ^{2}.$

Перестановка дает

${\frac {d\phi }{dt}}={\frac {c}{r\sin \theta }}{\sqrt {1-{\frac {r_{\text{s}}}{r}}}}.$

Для дальнейшего нам понадобится соотношение ${\frac {d\phi }{dt}}$. Для его нахождения воспользуемся уравнением радиальных геодезических

${\frac {d^{2}r}{d\tau ^{2}}}+\Gamma _{\mu \nu }^{r}u^{\mu }u^{\nu }=0.$

Не исчезающий $\Gamma$-коэффициенты связи

$\Gamma _{tt}^{r}={\frac {c^{2}BB'}{2}},\quad \Gamma _{rr}^{r}=-{\frac {B^{-1}B'}{2}},\quad \Gamma _{\theta \theta }^{r}=-rB,\quad \Gamma _{\phi \phi }^{r}=-Br\sin ^{2}\theta ,$

где $B'={\frac {dB}{dr}},\ B=1-{\frac {r_{\text{s}}}{r}}$.

Мы рассматриваем фотонные радиальные геодезические с постоянными r и $\theta$, поэтому

${\frac {dr}{d\tau }}={\frac {d^{2}r}{d\tau ^{2}}}={\frac {d\theta }{d\tau }}=0.$

Подставив все это в уравнение радиальной геодезической (уравнение геодезической с радиальной координатой в качестве зависимой переменной), получим

$\left({\frac {d\phi }{dt}}\right)^{2}={\frac {c^{2}r_{\text{s}}}{2r^{3}\sin ^{2}\theta }}.$

Сравнивая его с тем, что было получено ранее, имеем

$c{\sqrt {\frac {r_{\text{s}}}{2r}}}=c{\sqrt {1-{\frac {r_{\text{s}}}{r}}}},$

куда мы вставили $\theta =\pi /2$ радиан (представьте, что центральная масса, вокруг которой вращается фотон, расположена в центре осей координат. Тогда, когда фотон движется вдоль $\phi$-координатной линии, чтобы масса располагалась непосредственно в центре орбиты фотона, необходимо иметь $\theta =\pi /2$ радианы).

Следовательно, перестановка этого окончательного выражения дает

$r={\frac {3}{2}}r_{\text{s}},$

что и является результатом, который мы намеревались доказать.

Фотон вращается вокруг черной дыры Керра

Виды сбоку (слева) и сверху на столб (справа). Вращающаяся черная дыра имеет 9 радиусов, между которыми свет может вращаться по постоянной координате r . В этой анимации все орбиты фотонов для a = M. показаны

В отличие от черной дыры Шварцшильда, черная дыра Керра (вращающаяся) не имеет сферической симметрии, а имеет только ось симметрии, что имеет глубокие последствия для орбит фотонов, см., например, Крамера. для получения подробной информации и моделирования фотонных орбит и фотонных кругов. В экваториальной плоскости существуют две круговые фотонные орбиты (прямая и ретроградная) с разными Бойера – Линдквиста радиусами :

$r_{\pm }^{\circ }=r_{\text{s}}\left[1+\cos \left({\frac {2}{3}}\arccos {\frac {\pm |a|}{M}}\right)\right],$

где $a=J/M$ — угловой момент единицы массы черной дыры. Существуют и другие орбиты постоянного радиуса, но они имеют более сложные траектории и колеблются по широте вокруг экватора.

Внешние ссылки

• Шаг за шагом в черную дыру
• Виртуальные путешествия к черным дырам и нейтронным звездам
• Путеводитель по черным дырам
• Сферические фотоны вращаются вокруг черной дыры Керра