Метрика Керра

Метрика Керра или геометрия Керра описывает геометрию пустого пространства-времени вокруг вращающейся незаряженной аксиально-симметричной черной дыры с квазисферическим горизонтом событий . Керра Метрика является точным решением уравнений поля Эйнштейна общей теории относительности ; эти уравнения сильно нелинейны , что затрудняет поиск точных решений.

Обзор

Метрика Керра — это обобщение на вращающееся тело метрики Шварцшильда , открытой Карлом Шварцшильдом в 1915 году, которая описывала геометрию пространства-времени вокруг незаряженного, сферически симметричного и невращающегося тела. Вскоре после этого (1916–1918) было открыто соответствующее решение для заряженного сферического невращающегося тела — метрика Рейсснера — Нордстрема . Однако точное решение для незаряженной вращающейся черной дыры, метрика Керра, оставалось нерешенным до 1963 года, когда оно было обнаружено Роем Керром . Вскоре после этого, в 1965 году, было открыто естественное расширение заряженной вращающейся черной дыры, метрика Керра-Ньюмана . Эти четыре связанных решения можно резюмировать в следующей таблице, где Q тела представляет собой электрический заряд , а J представляет его спиновый угловой момент. :

	Невращающийся ( J = 0)	Вращающийся ( J ≠ 0)
Незаряженный ( Q = 0)	Шварцшильд	Керр
Заряжено ( Q ≠ 0)	Рейсснер – Нордстрем	Керр-Ньюман

Согласно метрике Керра, вращающееся тело должно демонстрировать перетаскивание системы отсчета (также известное как прецессия Лензе-Тирринга ), что является отличительным предсказанием общей теории относительности. Первое измерение этого эффекта перетаскивания кадров было сделано в 2011 году в ходе Gravity Probe B. эксперимента Грубо говоря, этот эффект предсказывает, что объекты, приближающиеся к вращающейся массе, будут вовлечены в ее вращение не из-за какой-либо приложенной силы или крутящего момента, которые можно почувствовать, а скорее из-за вихревой кривизны самого пространства-времени, связанной с вращающимися телами. . В случае вращающейся черной дыры на достаточно близких расстояниях все объекты – даже свет – должны вращаться вместе с черной дырой; область, где это происходит, называется эргосферой .

Свет от удаленных источников может несколько раз обойти горизонт событий (если достаточно близко); создание нескольких изображений одного и того же объекта . Для удаленного зрителя кажущееся перпендикулярное расстояние между изображениями уменьшается в e раз. ^{14:00 ​} (около 500). Однако быстро вращающиеся черные дыры имеют меньшее расстояние между изображениями множественности.

Вращающиеся черные дыры имеют поверхности, на которых метрика имеет явные сингулярности ; черной дыры размер и форма этих поверхностей зависят от массы и углового момента . Внешняя поверхность окружает эргосферу и имеет форму, подобную приплюснутой сфере. Внутренняя поверхность отмечает горизонт событий ; объекты, попадающие внутрь этого горизонта, никогда больше не смогут общаться с миром за пределами этого горизонта. Однако ни одна из поверхностей не является истинной особенностью, поскольку их кажущаяся особенность может быть устранена в другой системе координат . Аналогичная ситуация возникает при рассмотрении метрики Шварцшильда , которая также приводит к сингулярности при $r=r_{\text{s}}$ разделение пространства над и под r _s на два несвязанных участка; используя другое преобразование координат, можно затем связать расширенный внешний участок с внутренним (см. метрику Шварцшильда § Сингулярности и черные дыры ) – такое преобразование координат устраняет кажущуюся сингулярность в месте соединения внутренней и внешней поверхностей. Объекты между этими двумя поверхностями должны вращаться вместе с вращающейся черной дырой, как отмечалось выше; эта особенность в принципе может быть использована для извлечения энергии из вращающейся черной дыры вплоть до ее инвариантной массы энергии Mc . ² .

Эксперимент LIGO, впервые обнаруживший гравитационные волны, о котором было объявлено в 2016 году, также обеспечил первое прямое наблюдение пары черных дыр Керра.

Метрика

Метрика Керра обычно выражается в одной из двух форм: форме Бойера-Линдквиста и форме Керра-Шилда. Его можно легко получить из метрики Шварцшильда с помощью алгоритма Ньюмана – Джениса. формализмом Ньюмана-Пенроуза (также известным как формализм спин-коэффициента), уравнение Эрнста , или преобразование координат эллипсоида.

-

Основная статья: координаты Бойера – Линдквиста

Метрика Керра описывает геометрию пространства-времени вблизи массы $M$ вращающийся с угловым моментом $J$. Метрика (или, что эквивалентно, ее линейный элемент для собственного времени ) в координатах Бойера – Линдквиста равна

${\begin{aligned}ds^{2}&=-c^{2}d\tau ^{2}\\&=-\left(1-{\frac {r_{\text{s}}r}{\Sigma }}\right)c^{2}dt^{2}+{\frac {\Sigma }{\Delta }}dr^{2}+\Sigma d\theta ^{2}+\left(r^{2}+a^{2}+{\frac {r_{\text{s}}ra^{2}}{\Sigma }}\sin ^{2}\theta \right)\sin ^{2}\theta \ d\phi ^{2}-{\frac {2r_{\text{s}}ra\sin ^{2}\theta }{\Sigma }}c\,dt\,d\phi \end{aligned}}$ ( 1 )

где координаты $r,\theta ,\phi$ — стандартные сплюснутые сфероидальные координаты , эквивалентные декартовым координатам.

$x={\sqrt {r^{2}+a^{2}}}\sin \theta \cos \phi$ ( 2 )

$y={\sqrt {r^{2}+a^{2}}}\sin \theta \sin \phi$ ( 3 )

$z=r\cos \theta ,$ ( 4 )

где $r_{\text{s}}$ это радиус Шварцшильда

$r_{\text{s}}={\frac {2GM}{c^{2}}},$ ( 5 )

и где для краткости длина масштабируется $a,\Sigma$ и $\Delta$ были представлены как

$a={\frac {J}{Mc}},$ ( 6 )

$\Sigma =r^{2}+a^{2}\cos ^{2}\theta ,$ ( 7 )

$\Delta =r^{2}-r_{\text{s}}r+a^{2}.$ ( 8 )

Ключевой особенностью, которую следует отметить в приведенном выше показателе, является перекрестный $dt\,d\phi$. Это означает, что существует связь между временем и движением в плоскости вращения, которая исчезает, когда угловой момент черной дыры обращается в ноль.

В нерелятивистском пределе, где $M$ (или, что то же самое, $r_{\text{s}}$) обращается в ноль, метрика Керра становится ортогональной метрикой для сплюснутых сфероидальных координат

$g\mathop {\longrightarrow } _{M\to 0}-c^{2}dt^{2}+{\frac {\Sigma }{r^{2}+a^{2}}}dr^{2}+\Sigma d\theta ^{2}+\left(r^{2}+a^{2}\right)\sin ^{2}\theta d\phi ^{2}$ ( 9 )

Координаты Керра-Шилда

Метрику Керра можно выразить в форме «Керра – Шилда» , используя определенный набор декартовых координат следующим образом. Эти решения были предложены Керром и Шилдом в 1965 году.

$g_{\mu \nu }=\eta _{\mu \nu }+fk_{\mu }k_{\nu }\!$ ( 10 )

$f={\frac {2GMr^{3}}{r^{4}+a^{2}z^{2}}}$ ( 11 )

$\mathbf {k} =(k_{x},k_{y},k_{z})=\left({\frac {rx+ay}{r^{2}+a^{2}}},{\frac {ry-ax}{r^{2}+a^{2}}},{\frac {z}{r}}\right)$ ( 12 )

$k_{0}=1.\!$ ( 13 )

Обратите внимание, что k — единичный 3-вектор , что делает 4-вектор нулевым вектором как по отношению к g , так и по η . Здесь M — постоянная масса вращающегося объекта, η — тензор Минковского , а — постоянный параметр вращения вращающегося объекта. Понятно, что вектор ${\vec {a}}$ направлен вдоль положительной оси z. Величина r не является радиусом, а неявно определяется формулой

${\frac {x^{2}+y^{2}}{r^{2}+a^{2}}}+{\frac {z^{2}}{r^{2}}}=1$ ( 14 )

Обратите внимание, что величина r становится обычным радиусом R

$r\to R={\sqrt {x^{2}+y^{2}+z^{2}}}$

когда параметр вращения $a$ приближается к нулю. В этом виде решения единицы выбираются так, чтобы скорость света была равна единице ( $c=1$). На больших расстояниях от источника ( R ≫ a ) эти уравнения сводятся к форме Эддингтона–Финкельштейна метрики Шварцшильда .

В форме Керра–Шилда метрики Керра определитель метрического тензора всюду равен отрицательному, даже вблизи источника.

Координаты солитона

Поскольку метрика Керра (наряду с метрикой Керра – NUT ) аксиально симметрична, ее можно привести к форме, к которой преобразование Белинского – Захарова можно применить . Это означает, что черная дыра Керра имеет форму гравитационного солитона .

Масса вращательной энергии

Если полная энергия вращения $E_{\rm {rot}}=c^{2}\left(M-M_{\rm {irr}}\right)$ черной дыры извлекается, например, с помощью процесса Пенроуза , оставшаяся масса не может уменьшиться ниже неуменьшаемой массы. Следовательно, если черная дыра вращается со спином $a=M$, его полный массовый эквивалент $M$ выше в раз ${\sqrt {2}}$ по сравнению с соответствующей черной дырой Шварцшильда, где $M$ равно $M_{\text{irr}}$. Причина этого в том, что для того, чтобы заставить статическое тело вращаться, к системе необходимо приложить энергию. Из-за эквивалентности массы и энергии эта энергия также имеет эквивалент массы, который добавляется к общей массе-энергии системы: $M$.

Общий массовый эквивалент $M$ (гравитирующая масса) тела (включая его энергию вращения ) и его неуменьшаемая масса $M_{\text{irr}}$ связаны

$2M_{\rm {irr}}^{2}=M^{2}+{\sqrt {M^{4}-J^{2}c^{2}/G^{2}}}\Longrightarrow M^{2}=M_{\rm {irr}}^{2}+{\frac {J^{2}c^{2}}{4M_{\rm {irr}}^{2}G^{2}}}.$

Волновой оператор

Поскольку даже прямая проверка метрики Керра требует громоздких вычислений, контравариантные компоненты $g^{ik}$ метрического тензора в координатах Бойера–Линдквиста показаны ниже в выражении для квадрата четырехградиентного оператора :

$g^{\mu \nu }{\frac {\partial }{\partial x^{\mu }}}{\frac {\partial }{\partial x^{\nu }}}=-{\frac {1}{c^{2}\Delta }}\left(r^{2}+a^{2}+{\frac {r_{\text{s}}ra^{2}}{\Sigma }}\sin ^{2}\theta \right)\left({\frac {\partial }{\partial t}}\right)^{2}-{\frac {2r_{\text{s}}ra}{c\Sigma \Delta }}{\frac {\partial }{\partial \phi }}{\frac {\partial }{\partial {t}}}+{\frac {1}{\Delta \sin ^{2}\theta }}\left(1-{\frac {r_{\text{s}}r}{\Sigma }}\right)\left({\frac {\partial }{\partial \phi }}\right)^{2}+{\frac {\Delta }{\Sigma }}\left({\frac {\partial }{\partial r}}\right)^{2}+{\frac {1}{\Sigma }}\left({\frac {\partial }{\partial \theta }}\right)^{2}$ ( 15 )

Перетаскивание кадра

Мы можем переписать метрику Керра ( 1 ) в следующем виде:

$c^{2}d\tau ^{2}=\left(g_{tt}-{\frac {g_{t\phi }^{2}}{g_{\phi \phi }}}\right)dt^{2}+g_{\mathrm {rr} }dr^{2}+g_{\theta \theta }d\theta ^{2}+g_{\phi \phi }\left(d\phi +{\frac {g_{t\phi }}{g_{\phi \phi }}}dt\right)^{2}.$ ( 16 )

Эта метрика эквивалентна вращающейся в одном направлении системе отсчета, которая вращается с угловой скоростью Ω, которая зависит как от радиуса r , так и от широты   θ , где Ω называется горизонтом Киллинга .

$\Omega =-{\frac {g_{t\phi }}{g_{\phi \phi }}}={\frac {r_{\text{s}}rac}{\Sigma \left(r^{2}+a^{2}\right)+r_{\text{s}}ra^{2}\sin ^{2}\theta }}.$ ( 17 )

Таким образом, инерциальная система отсчета увлекается вращающейся центральной массой и участвует во вращении последней; это называется перетаскиванием кадров и проверено экспериментально. Качественно перетаскивание кадров можно рассматривать как гравитационный аналог электромагнитной индукции. «Конькобежка», находящаяся на орбите над экватором и покоящаяся относительно звезд, вытягивает руки. Рука, вытянутая в сторону черной дыры, будет повернута по направлению вращения. Рука, вытянутая в сторону от черной дыры, будет повернута против вращения. Поэтому ее вращение будет ускорено, в противоположном направлении по отношению к черной дыре. Это противоположно тому, что происходит в повседневной жизни. Если она уже вращается с определенной скоростью, когда вытягивает руки, инерционные эффекты и эффекты перетаскивания кадра уравновесятся, и ее вращение не изменится. Из-за принципа эквивалентности гравитационные эффекты локально неотличимы от инерционных эффектов, поэтому эта скорость вращения, при которой, когда она вытягивает руки, ничего не происходит, является ее локальным эталоном отсутствия вращения. Эта система отсчета вращается относительно неподвижных звезд и вращается в противоположном направлении относительно черной дыры. Полезная метафора – это планетарная система передач, в которой черная дыра является солнечной шестерней, фигурист — планетарной шестерней, а внешняя вселенная — кольцевой шестерней. Это также можно интерпретировать через принцип Маха .

Важные поверхности

Расположение горизонтов, эргосфер и кольцевой сингулярности керровского пространства-времени в декартовых координатах Керра – Шильда.

Сравнение тени (черной) и важных поверхностей (белых) черной дыры. Параметр вращения $a$ анимировано из $0$ к $M$, а левая сторона черной дыры вращается в сторону наблюдателя.

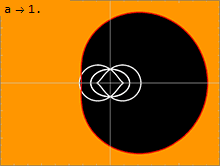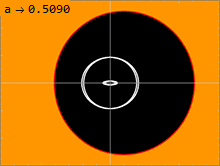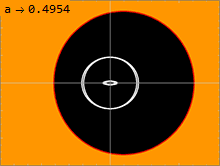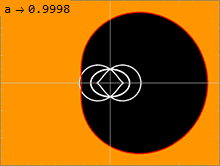
) есть несколько важных поверхностей В метрике Керра ( 1 . Внутренняя поверхность соответствует горизонту событий, подобному наблюдаемому в метрике Шварцшильда ; это происходит там, где чисто радиальная составляющая g _rr метрики стремится к бесконечности. Решение квадратного уравнения 1 / g _rr = 0 дает решение:

$r_{\rm {H}}^{\pm }={\frac {r_{\text{s}}\pm {\sqrt {r_{\text{s}}^{2}-4a^{2}}}}{2}}$

что в натуральных единицах (которые дают $G=M=c=1$) упрощается до:

$r_{\rm {H}}^{\pm }=1\pm {\sqrt {1-a^{2}}}$

Если в метрике Шварцшильда горизонт событий является также местом, где чисто временная составляющая g _tt метрики меняет знак с положительного на отрицательный, то в метрике Керра это происходит на другом расстоянии. Снова решая квадратное уравнение {{nowrap1= g _tt = 0}} дает решение:

$r_{\rm {E}}^{\pm }={\frac {r_{\text{s}}\pm {\sqrt {r_{\text{s}}^{2}-4a^{2}\cos ^{2}\theta }}}{2}}$

или в натуральных единицах:

$r_{\rm {E}}^{\pm }=1\pm {\sqrt {1-a^{2}\cos ^{2}\theta }}$

Из-за того, что ² Член θ в квадратном корне, эта внешняя поверхность напоминает сплющенную сферу, которая касается внутренней поверхности в полюсах оси вращения, где широта θ равна 0 или π ; пространство между этими двумя поверхностями называется эргосферой . В этом объеме чисто временная компонента g _tt отрицательна, т. е. действует как чисто пространственная метрическая компонента. Следовательно, частицы внутри этой эргосферы должны вращаться вместе с внутренней массой, если они хотят сохранить свой времяподобный характер. Движущаяся частица испытывает положительное собственное время вдоль своей мировой линии , своего пути в пространстве-времени . Однако это невозможно в эргосфере, где g _tt отрицательно, если только частица не вращается вокруг внутренней массы. $M$ с угловой скоростью не менее $\Omega$. Таким образом, ни одна частица не может двигаться в направлении, противоположном вращению центральной массы внутри эргосферы.

Как и в случае с горизонтом событий в метрике Шварцшильда , кажущаяся особенность в r _H обусловлена ​​выбором координат (т. е. это координатная особенность ). Фактически, пространство-время можно плавно продолжить через него при соответствующем выборе координат. В свою очередь внешняя граница эргосферы в точке r _E сама по себе не является сингулярной даже в керровских координатах из-за ненулевой $dt\ d\phi$ срок.

процесс

Основная статья: Процесс Пенроуза

Черная дыра вообще окружена поверхностью, называемой горизонтом событий и расположенной на радиусе Шварцшильда для невращающейся черной дыры, где скорость убегания равна скорости света. Внутри этой поверхности ни один наблюдатель/частица не может сохранять постоянный радиус. Он вынужден падать внутрь, поэтому это иногда называют статическим пределом .

Вращающаяся черная дыра имеет тот же статический предел на горизонте событий, но за пределами горизонта событий имеется дополнительная поверхность, называемая «эргоповерхностью», определяемая формулой

$(r-M)^{2}=M^{2}-J^{2}\cos ^{2}\theta$

в координатах Бойера – Линдквиста , которые можно интуитивно охарактеризовать как сферу, в которой «скорость вращения окружающего пространства» увлекается вместе со скоростью света. Внутри этой сферы сопротивление превышает скорость света, и любой наблюдатель/частица вынужден вращаться вместе.

Область за пределами горизонта событий, но внутри поверхности, где скорость вращения равна скорости света, называется эргосферой ( от греческого ergon, что означает работа ). Частицы, попадающие в эргосферу, вынуждены вращаться быстрее и тем самым набирать энергию. Поскольку они все еще находятся за горизонтом событий, они могут выбраться из черной дыры. Суть процесса заключается в том, что вращающаяся черная дыра испускает энергичные частицы за счет своей собственной полной энергии. Возможность извлечения энергии вращения из вращающейся черной дыры была впервые предложена математиком Роджером Пенроузом в 1969 году и поэтому названа процессом Пенроуза . Вращающиеся черные дыры в астрофизике являются потенциальным источником большого количества энергии и используются для объяснения энергетических явлений, таких как гамма-всплески .

Особенности геометрии Керра

Геометрия Керра демонстрирует множество примечательных особенностей: максимальное аналитическое расширение включает последовательность асимптотически плоских внешних областей, каждая из которых связана с эргосферой , стационарными предельными поверхностями, горизонтами событий , горизонтами Коши , замкнутыми времениподобными кривыми и кольцеобразной сингулярностью кривизны . Уравнение геодезических можно решить точно в замкнутой форме. Помимо двух векторных полей Киллинга (соответствующих сдвигу времени и осевой симметрии ), геометрия Керра допускает замечательный тензор Киллинга . Существует пара главных нулевых сравнений (одно входящее и одно исходящее ). Тензор Вейля является алгебраически специальным фактически он имеет тип Петрова D. , Глобальная структура известна. Топологически гомотопический тип пространства-времени Керра можно просто охарактеризовать как линию с окружностями, прикрепленными к каждой целочисленной точке.

Заметим, что внутренняя геометрия Керра неустойчива по отношению к возмущениям во внутренней области. Эта нестабильность означает, что, хотя метрика Керра является осесимметричной, черная дыра, созданная в результате гравитационного коллапса, может быть не такой. Эта нестабильность также означает, что многие из описанных выше особенностей геометрии Керра могут отсутствовать внутри такой черной дыры.

Поверхность, по которой свет может вращаться вокруг черной дыры, называется фотонной сферой. Решение Керра имеет бесконечно много фотонных сфер , лежащих между внутренней и внешней. В невращающемся решении Шварцшильда с $a=0$, внутренняя и внешняя фотонные сферы вырождаются, так что на одном радиусе остается только одна фотонная сфера. Чем больше вращение черной дыры, тем дальше друг от друга движутся внутренняя и внешняя фотонные сферы. Луч света, движущийся в направлении, противоположном вращению черной дыры, будет вращаться вокруг дыры во внешней фотонной сфере. Луч света, движущийся в том же направлении, что и вращение черной дыры, будет вращаться вокруг внутренней фотонной сферы. Орбитальные геодезические с некоторым угловым моментом, перпендикулярным оси вращения черной дыры, будут вращаться по фотонным сферам между этими двумя крайностями. Поскольку пространство-время вращается, такие орбиты демонстрируют прецессию, поскольку происходит сдвиг $\phi$ переменная после завершения одного периода в $\theta$ переменная.

траектории

Анимация орбиты тестовой частицы вокруг вращающейся черной дыры. Слева: вид сверху, справа: вид сбоку.

Еще одна траектория пробной массы вокруг вращающейся черной дыры (Керра). В отличие от орбит вокруг черной дыры Шварцшильда, орбита не ограничена одной плоскостью, а эргодически заполняет тороподобную область вокруг экватора.

Уравнения движения пробных частиц в пространстве-времени Керра определяются четырьмя константами движения . Во-первых, это инвариантная масса $\mu$ пробной частицы, определяемой соотношением

$$-\mu ^{2}=p^{\alpha }g_{\alpha \beta }p^{\beta },$$

где $p^{\alpha }$ – четырехимпульс частицы. Кроме того, существуют две константы движения, заданные симметрией временного перевода и вращения керровского пространства-времени: энергия $E$, и составляющая орбитального углового момента, параллельная спине черной дыры $L_{z}$.

$$E=-p_{t},$$

и

$$L_{z}=p_{\phi }$$

Используя теорию Гамильтона-Якоби , Брэндон Картер показал, что существует четвертая константа движения, $Q$, теперь называется постоянной Картера . Он связан с полным угловым моментом частицы и определяется выражением

$$Q=p_{\theta }^{2}+\cos ^{2}\theta \left(a^{2}\left(\mu ^{2}-E^{2}\right)+\left({\frac {L_{z}}{\sin \theta }}\right)^{2}\right).$$

Поскольку существует четыре (независимые) константы движения для степеней свободы, уравнения движения пробной частицы в пространстве-времени Керра интегрируемы .

Используя эти константы движения, можно записать уравнения траектории пробной частицы (используя натуральные единицы измерения). $G=M=c=1$),

$${\begin{aligned}\Sigma {\frac {dr}{d\lambda }}&=\pm {\sqrt {R(r)}}\\\Sigma {\frac {d\theta }{d\lambda }}&=\pm {\sqrt {\Theta (\theta )}}\\\Sigma {\frac {d\phi }{d\lambda }}&=-\left(aE-{\frac {L_{z}}{\sin ^{2}\theta }}\right)+{\frac {a}{\Delta }}P(r)\\\Sigma {\frac {dt}{d\lambda }}&=-a\left(aE\sin ^{2}\theta -L_{z}\right)+{\frac {r^{2}+a^{2}}{\Delta }}P(r)\end{aligned}}$$

с

• $\Theta (\theta )=Q-\cos ^{2}\theta \left(a^{2}\left(\mu ^{2}-E^{2}\right)+{\frac {L_{z}^{2}}{\sin ^{2}\theta }}\right)$
• $P(r)=E\left(r^{2}+a^{2}\right)-aL_{z}$
• $R(r)=P(r)^{2}-\Delta \left(\mu ^{2}r^{2}+(L_{z}-aE)^{2}+Q\right)$

где $\lambda$ – аффинный параметр такой, что ${\frac {dx^{\alpha }}{d\lambda }}=p^{\alpha }$. В частности, когда $\mu >0$ аффинный параметр $\lambda$, связано с собственным временем $\tau$ через $\lambda =\tau /\mu$.

Из-за эффекта перетаскивания системы координат наблюдатель с нулевым угловым моментом (ЗАМО) вращается с угловой скоростью $\Omega$ которое определяется относительно координатного времени бухгалтера $t$. Локальная скорость $v$ тест-частицы измеряется относительно зонда, вращающегося со скоростью $\Omega$. Гравитационное замедление времени между ЗАМО при фиксированной $r$ а неподвижный наблюдатель вдали от массы

$${\frac {t}{\tau }}={\sqrt {\frac {\left(a^{2}+r^{2}\right)^{2}-a^{2}\Delta \sin ^{2}\theta }{\Delta \ \Sigma }}}.$$

В декартовых координатах Керра – Шилда уравнения фотона имеют вид

$${\ddot {x}}+i{\ddot {y}}=4iMa{\frac {r}{\Sigma ^{2}}}W\left[{\dot {x}}+i{\dot {y}}-{\frac {x+iy}{r}}{\dot {r}}\right]-M(x+iy)\left({\frac {4r^{2}}{\Sigma }}-1\right){\frac {C-a^{2}W^{2}}{r\Sigma ^{2}}}$$

$${\ddot {z}}=-Mz\left({\frac {4r^{2}}{\Sigma }}-1\right){\frac {C}{r\Sigma ^{2}}}$$

где $C$ аналогична постоянной Картера и $W$ это полезная величина

$$C=p_{\theta }^{2}+\left(aE\sin {\theta }-{\frac {L_{z}}{\sin {\theta }}}\right)^{2}$$

$$W={\dot {t}}-a\sin ^{2}{\theta }{\dot {\phi }}$$

Если мы установим $a=0$, геодезические Шварцшильда восстановлены.

Симметрии

Группа изометрий метрики Керра — это подгруппа десятимерной группы Пуанкаре, переводящая двумерное локус особенности в себя. Он сохраняет перемещение времени (одно измерение) и вращение вокруг своей оси вращения (одно измерение). Таким образом, оно имеет два измерения. Как и группа Пуанкаре, она имеет четыре связных компонента: компонент тождества; компонент, меняющий время и долготу; компонент, отражающийся через экваториальную плоскость; и компонент, который делает и то, и другое.

В физике симметрии обычно связаны с сохраняющимися константами движения в соответствии с теоремой Нётер . Как показано выше, уравнения геодезических имеют четыре сохраняющихся величины: одна из которых вытекает из определения геодезической, а две из которых возникают из симметрии перевода во времени и вращения геометрии Керра. Четвертая сохраняющаяся величина не возникает из-за симметрии в обычном смысле этого слова и обычно называется скрытой симметрией.

Керра

Расположение горизонта событий определяется большим корнем из $\Delta =0$. Когда $r_{\text{s}}/2<a$ (т.е. $GM^{2}<Jc$), у этого уравнения нет (действительнозначных) решений и нет горизонта событий. Не имея горизонтов событий, которые могли бы скрыть ее от остальной Вселенной, черная дыра перестает быть черной дырой и вместо этого становится голой сингулярностью .

Черные дыры

Хотя решение Керра кажется сингулярным в корнях $\Delta =0$, это на самом деле координатные особенности , и при соответствующем выборе новых координат решение Керра можно плавно продолжить через значения $r$ соответствующие этим корням. Больший из этих корней определяет расположение горизонта событий, а меньший — горизонта Коши . Кривая (направленная в будущее, подобная времени) может начинаться снаружи и проходить через горизонт событий. Пройдя через горизонт событий, $r$ координата теперь ведет себя как координата времени, поэтому она должна уменьшаться до тех пор, пока кривая не пройдет через горизонт Коши.

Область за горизонтом Коши имеет несколько удивительных особенностей. $r$ координата снова ведет себя как пространственная координата и может свободно изменяться. Внутренняя область имеет симметрию отражения, так что кривая (направленная в будущее, подобная времени) может продолжаться по симметричному пути, который продолжается через второй горизонт Коши, через второй горизонт событий и выходит в новую внешнюю область, которая изометрична исходной внешней области решения Керра. Затем кривая может уйти в бесконечность в новом регионе или войти в будущий горизонт событий нового внешнего региона и повторить процесс. Эту вторую внешность иногда считают другой вселенной. С другой стороны, в решении Керра особенность представляет собой кольцо и кривая может проходить через центр этого кольца. В области за пределами возможны замкнутые времяподобные кривые. Поскольку траектории наблюдателей и частиц в общей теории относительности описываются времяподобными кривыми, наблюдатели в этой области могут вернуться в свое прошлое. Это внутреннее решение вряд ли является физическим и рассматривается как чисто математический артефакт.

Хотя ожидается, что внешняя область решения Керра стабильна и что все вращающиеся черные дыры в конечном итоге приблизятся к метрике Керра, внутренняя область решения кажется нестабильной, во многом подобно карандашу, балансирующему на острие. Это связано с идеей космической цензуры .

с другими

Геометрия Керра является частным примером стационарного аксиально-симметричного вакуумного решения уравнения поля Эйнштейна . Семейство всех стационарных аксиально-симметричных вакуумных решений уравнения поля Эйнштейна представляет собой вакуум Эрнста .

Решение Керра также связано с различными невакуумными решениями, моделирующими черные дыры. Например, электровакуум Керра-Ньюмана моделирует (вращающуюся) черную дыру, наделенную электрическим зарядом, а нулевая пыль Керра-Вайдьи моделирует (вращающуюся) дыру с падающим электромагнитным излучением.

Особый случай $a=0$ метрики Керра дает метрику Шварцшильда , которая моделирует невращающуюся черную дыру, статическую и сферически симметричную , в координатах Шварцшильда . (В этом случае каждый момент Героха, кроме массы, исчезает.)

Внутренняя часть геометрии Керра, или, скорее, ее часть, локально изометрична вакууму Чандрасекара-Феррари CPW , примеру модели сталкивающихся плоских волн . Это особенно интересно, поскольку глобальная структура этого решения CPW сильно отличается от структуры геометрии Керра, и в принципе экспериментатор мог бы надеяться изучить геометрию (внешней части) внутренней части Керра, организовав столкновение две подходящие гравитационные плоские волны .

Многополюсные моменты

Каждый асимптотически плоский вакуум Эрнста можно охарактеризовать бесконечной последовательностью релятивистских мультипольных моментов , первые два из которых можно интерпретировать как массу и угловой момент источника поля. Существуют альтернативные формулировки релятивистских мультипольных моментов Хансена, Торна и Героха, которые, как оказалось, согласуются друг с другом. Релятивистские мультипольные моменты геометрии Керра были вычислены Хансеном; они оказываются

$M_{n}=M[ia]^{n}$

Таким образом, частный случай вакуума Шварцшильда ( $a=0$) дает «монопольный точечный источник » общей теории относительности.

Мультипольные моменты Вейля возникают в результате обработки определенной метрической функции (формально соответствующей ньютоновскому гравитационному потенциалу), которая представляет собой диаграмму Вейля – Папапетру для семейства Эрнста всех стационарных осесимметричных вакуумных решений с использованием стандартных евклидовых скалярных мультипольных моментов . Они отличаются от моментов, вычисленных Хансеном выше. В каком-то смысле моменты Вейля лишь (косвенно) характеризуют «распределение масс» изолированного источника и оказываются зависящими только от релятивистских моментов четного порядка . В случае решений, симметричных относительно экваториальной плоскости, моменты Вейля нечетного порядка исчезают. Для вакуумных решений Керра первые несколько моментов Вейля определяются выражением

$a_{0}=M,\qquad a_{1}=0,\qquad a_{2}=M\left({\frac {M^{2}}{3}}-a^{2}\right)$

В частности, мы видим, что вакуум Шварцшильда имеет ненулевой момент Вейля второго порядка, что соответствует тому факту, что «монополь Вейля» представляет собой вакуумное решение Чази – Керзона , а не вакуумное решение Шварцшильда, которое возникает из ньютоновского потенциала некоторой конечной длина, равномерная плотность, тонкий стержень .

В общей теории относительности слабого поля удобно рассматривать изолированные источники, используя другой тип мультиполя, который обобщает моменты Вейля до моментов мультиполя массы и моментов мультиполя импульса , характеризующих соответственно распределение массы и импульса источника. Это многоиндексные величины, чьи соответствующим образом симметризованные и антисимметризованные части могут быть связаны с действительными и мнимыми частями релятивистских моментов для полной нелинейной теории довольно сложным образом.

Перес и Морески дали альтернативное понятие «монопольных решений», расширив стандартную NP-тетраду вакуума Эрнста по степеням $r$ (радиальная координата на карте Вейля – Папапетру). Согласно этой формулировке:

• изолированный источник монополя массы с нулевым угловым моментом представляет собой семейство вакуумов Шварцшильда (один параметр),
• изолированный источник монополя массы с радиальным угловым моментом представляет собой семейство вакуумов Тауба – НУТ (два параметра; не совсем асимптотически плоский),
• изолированный источник монополя массы с осевым угловым моментом представляет собой семейство вакуумов Керра (два параметра).

В этом смысле вакуум Керра представляет собой простейшее стационарное осесимметричное асимптотически плоское вакуумное решение в общей теории относительности.

Открытые проблемы

Геометрия Керра часто используется в качестве модели вращающейся черной дыры , но если решение считается справедливым только за пределами некоторой компактной области (с некоторыми ограничениями), в принципе, ее можно использовать в качестве внешнего решения для моделировать гравитационное поле вокруг вращающегося массивного объекта, отличного от черной дыры, такого как нейтронная звезда или Земля. Это очень хорошо работает для невращающегося случая, когда внешний вакуум Шварцшильда может быть сопоставлен с внутренней частью шварцшильдовской жидкости и, более того, с более общими идеальной жидкости статическими сферически-симметричными решениями . Однако проблема поиска вращающейся внутренней идеальной жидкости, которая могла бы быть согласована с экстерьером Керра или даже с любым асимптотически плоским вакуумным внешним решением, оказалась очень сложной. В частности, теперь известно, что жидкость Уолквиста , которая когда-то считалась кандидатом на сопоставление с экстерьером Керра, не допускает такого сопоставления. В настоящее время, по-видимому, известны лишь приближенные решения, моделирующие медленно вращающиеся жидкие шары (это релятивистский аналог сплюснутых сфероидальных шаров с ненулевой массой и угловым моментом, но исчезающими высшими мультипольными моментами). Однако внешний вид Диск Нойгебауэра – Мейнеля , точное пылевое решение , моделирующее вращающийся тонкий диск, в предельном случае приближается к $GM^{2}=cJ$ Керровская геометрия. Известны также физические решения тонкого диска, полученные путем идентификации частей керровского пространства-времени.

См. также

• Метрика Шварцшильда
• Метрика Керра – Ньюмана
• Метрика Рейсснера – Нордстрема
• Метрика Хартла – Торна
• Спин-флип
• Вращающаяся черная дыра

Дальнейшее чтение

• Уилтшир, Дэвид Л.; Виссер, Мэтт; Скотт, Сьюзен М. , ред. (2009). Пространство-время Керра: вращающиеся черные дыры в общей теории относительности . Кембридж: Издательство Кембриджского университета. ISBN  978-0-521-88512-6 .
• Стефани, Ганс; Крамер, Дитрих; МакКаллум, Малькольм; Хоэнселерс, Корнелиус; Херлт, Эдуард (2003). Точные решения уравнений поля Эйнштейна . Кембридж: Издательство Кембриджского университета. ISBN  978-0-521-46136-8 .
• Мейнель, Рейнхард ; Ансорг, Маркус; Кляйнвахтер, Андреас; Нойгебауэр, Гернот; Петров, Дэвид (2008). Релятивистские фигуры равновесия . Кембридж: Издательство Кембриджского университета. ISBN  978-0-521-86383-4 .
• О'Нил, Барретт (1995). Геометрия керровских черных дыр . Уэлсли, Массачусетс: АК Питерс. ISBN  978-1-56881-019-5 .
• Д'Инверно, Рэй (1992). Знакомство с теорией относительности Эйнштейна . Оксфорд: Кларендон Пресс. ISBN  978-0-19-859686-8 . См. главу 19 для ознакомления с введением на продвинутом уровне бакалавриата.
• Чандрасекхар, С. (1992). Математическая теория черных дыр . Оксфорд: Кларендон Пресс. ISBN  978-0-19-850370-5 . См. главы 6-10 для более тщательного изучения на продвинутом уровне магистратуры.
• Гриффитс, Дж. Б. (1991). Столкновение плоских волн в общей теории относительности . Оксфорд: Издательство Оксфордского университета. ISBN  978-0-19-853209-5 . См. главу 13 для модели Chandrasekhar/Ferrari CPW.
• Адлер, Рональд; Базен, Морис; Шиффер, Менахем (1975). Введение в общую теорию относительности (второе изд.). Нью-Йорк: МакГроу-Хилл. ISBN  978-0-07-000423-8 . См. главу 7 .
• Пенроуз, Р. (1968). под ред. К. де Витта и Дж. Уиллера (ред.). Баттель Реконтр . У.А. Бенджамин, Нью-Йорк. п. 222.
• Перес, Алехандро; Морески, Освальдо М. (2000). «Характеризация точных решений из асимптотических физических понятий». arXiv : gr-qc/0012100v1 . Характеристика трех стандартных семейств вакуумных растворов, как отмечалось выше.
• Сотириу, Томас П.; Апостолатос, Теохарис А. (2004). «Исправления и комментарии к мультипольным моментам осесимметричного электровакуумного пространства-времени». Сорт. Квантовая гравитация . 21 (24): 5727–5733. arXiv : gr-qc/0407064 . Бибкод : 2004CQGra..21.5727S . дои : 10.1088/0264-9381/21/24/003 . S2CID   16858122 . Дает релятивистские мультипольные моменты для вакуума Эрнста (плюс электромагнитный и гравитационно-релятивистский мультипольные моменты для заряженного обобщения).
• Картер, Б. (1971). «Осесимметричная черная дыра имеет только две степени свободы». Письма о физических отзывах . 26 (6): 331–333. Бибкод : 1971PhRvL..26..331C . doi : 10.1103/PhysRevLett.26.331 .
• Уолд, Р.М. (1984). Общая теория относительности . Чикаго: Издательство Чикагского университета. стр. 312–324. ISBN  978-0-226-87032-8 .
• Керр, Р.П.; Шильд, А. (2009). «Републикация: новый класс вакуумных решений уравнений поля Эйнштейна». Общая теория относительности и гравитация . 41 (10): 2485–2499. Бибкод : 2009GReGr..41.2485K . дои : 10.1007/s10714-009-0857-z . S2CID   361088 .
• Красинский, Анджей; Вердагер, Энрик; Керр, Рой Патрик (2009). «Примечание редакции: Р. П. Керр и А. Шилд, Новый класс вакуумных решений уравнений поля Эйнштейна» . Общая теория относительности и гравитация . 41 (10): 2469–2484. Бибкод : 2009GReGr..41.2469K . дои : 10.1007/s10714-009-0856-0 . "...Эта заметка призвана служить руководством для тех читателей, которые желают проверить все детали [вывода решения Керра]..."