Шварцшильдовская геодезия

В общей теории относительности геодезические Шварцшильда описывают движение пробных частиц в гравитационном поле центральной фиксированной массы. ${\textstyle M,}$ то есть движение в метрике Шварцшильда. Геодезические Шварцшильда сыграли решающую роль в подтверждении Эйнштейна общей теории относительности . Например, они обеспечивают точные предсказания аномальной прецессии планет Солнечной системы и отклонения света под действием гравитации.

Геодезические Шварцшильда относятся только к движению частиц столь малых масс, что они мало вносят вклад в гравитационное поле. Однако они очень точны во многих астрофизических сценариях при условии, что ${\textstyle m}$ во много раз меньше центральной массы ${\textstyle M}$, например, для планет, вращающихся вокруг своей звезды. Геодезические Шварцшильда также являются хорошим приближением относительного движения двух тел произвольной массы при условии, что масса Шварцшильда ${\textstyle M}$ устанавливается равным сумме двух отдельных масс ${\textstyle m_{1}}$ и ${\textstyle m_{2}}$. Это важно для предсказания движения двойных звезд в общей теории относительности.

Исторический контекст

Метрика Шварцшильда названа в честь своего первооткрывателя Карла Шварцшильда , который нашел решение в 1915 году, всего примерно через месяц после публикации общей теории относительности Эйнштейна. Это было первое точное решение уравнений поля Эйнштейна, отличное от тривиального решения в плоском пространстве .

В 1931 году Юсуке Хагихара опубликовал работу, показывающую, что траектория пробной частицы в метрике Шварцшильда может быть выражена через эллиптические функции .

Сэмюил Каплан в 1949 году показал, что существует минимальный радиус стабильной круговой орбиты в метрике Шварцшильда.

Метрика Шварцшильда

См. также: Метрика Шварцшильда и Получение решения Шварцшильда.

Точным решением уравнений поля Эйнштейна является метрика Шварцшильда , которая соответствует внешнему гравитационному полю незаряженного, невращающегося, сферически-симметричного тела массы. ${\textstyle M}$. Решение Шварцшильда можно записать как

$ds^{2}=c^{2}{d\tau }^{2}=\left(1-{\frac {r_{\text{s}}}{r}}\right)c^{2}dt^{2}-{\frac {dr^{2}}{1-{\frac {r_{\text{s}}}{r}}}}-r^{2}(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2})$

где

$\tau$, в случае пробной частицы небольшой положительной массы, — это собственное время (время, измеряемое часами, движущимися вместе с частицей) в секундах,

$c$ скорость света в метрах в секунду,

$t$ это для $r>r_{\text{s}}$, координата времени (время, измеряемое стационарными часами, находящимися на бесконечности) в секундах,

$r$ это для $r>r_{\text{s}}$, радиальная координата (окружность круга с центром в звезде, разделенная на $2\pi$) в метрах,

$\theta$ - широта (угол от севера) в радианах,

$\varphi$ - долгота в радианах, а

$r_{\text{s}}$ - радиус Шварцшильда массивного тела (в метрах), связанный с его массой ${\textstyle M}$ к

$r_{\text{s}}={\frac {2GM}{c^{2}}},$

где ${\textstyle G}$ является гравитационной постоянной . Классическая ньютоновская теория гравитации восстанавливается в пределе как соотношение ${\textstyle {\frac {r_{\text{s}}}{r}}}$ уходит в ноль. В этом пределе метрика возвращается к метрике, определенной специальной теорией относительности .

На практике это соотношение почти всегда крайне мало. Например, радиус Шварцшильда ${\textstyle r_{\text{s}}}$ Земли составляет примерно 9 мм ( 3/8 ; дюйма ) на поверхности Земли поправки к ньютоновской гравитации составляют лишь одну миллиардную часть. Радиус Шварцшильда Солнца гораздо больше, примерно 2953 метра, но на его поверхности соотношение ${\textstyle {\frac {r_{\text{s}}}{r}}}$ составляет примерно 4 части на миллион. Белый карлик гораздо плотнее, но даже здесь это соотношение на его поверхности составляет примерно 250 частей на миллион. Это соотношение становится большим только вблизи сверхплотных объектов, таких как нейтронные звезды (где соотношение составляет примерно 50%) и черные дыры .

Орбиты тестовых частиц

Сравнение орбиты пробной частицы в ньютоновском (слева) и шварцшильдовском (справа) пространстве-времени; обратите внимание на апсидальную прецессию справа.

Мы можем упростить проблему, используя симметрию и исключив из рассмотрения одну переменную. Поскольку метрика Шварцшильда симметрична относительно ${\textstyle \theta ={\frac {\pi }{2}}}$, любая геодезическая, которая начинает двигаться в этой плоскости, останется в этой плоскости на неопределенный срок (плоскость полностью геодезическая ). Поэтому ориентируем систему координат так, чтобы орбита частицы лежала в этой плоскости, и фиксируем ${\textstyle \theta }$ координировать, чтобы быть ${\textstyle {\frac {\pi }{2}}}$ так что метрика (этой плоскости) упрощается до

$c^{2}d\tau ^{2}=\left(1-{\frac {r_{\text{s}}}{r}}\right)c^{2}dt^{2}-{\frac {dr^{2}}{1-{\frac {r_{\text{s}}}{r}}}}-r^{2}d\varphi ^{2}.$

Две константы движения (значения, не меняющиеся с течением времени) $\tau$) можно идентифицировать (см. вывод, приведенный ниже ). Одна из них — полная энергия ${\textstyle E}$:

$\left(1-{\frac {r_{\text{s}}}{r}}\right){\frac {dt}{d\tau }}={\frac {E}{mc^{2}}}.$

а другой — удельный угловой момент :

$h={\frac {L}{\mu }}=r^{2}{\frac {d\varphi }{d\tau }},$

где ${\textstyle L}$ - общий угловой момент двух тел, и ${\textstyle \mu }$ это приведенная масса . Когда ${\textstyle M\gg m}$, приведенная масса примерно равна ${\textstyle m}$. Иногда предполагается, что ${\textstyle m=\mu }$. В случае планеты Меркурий это упрощение вносит ошибку, более чем в два раза превышающую релятивистский эффект. Говоря о геодезии, ${\textstyle m}$ можно считать фиктивным, и дело в константах ${\textstyle {\frac {E}{m}}}$ и ${\textstyle h}$. Чтобы охватить все возможные геодезические, нам необходимо рассмотреть случаи, когда ${\textstyle {\frac {E}{m}}}$ является бесконечной (дающей траектории фотонов ) или мнимой (для тахионной геодезической). Для фотонного случая нам также необходимо указать число, соответствующее отношению двух констант, а именно ${\textstyle {\frac {mh}{E}}}$, которое может быть нулем или ненулевым действительным числом.

Подставляя эти константы в определение метрики Шварцшильда

$c^{2}=\left(1-{\frac {r_{\text{s}}}{r}}\right)c^{2}\left({\frac {dt}{d\tau }}\right)^{2}-{\frac {1}{1-{\frac {r_{\text{s}}}{r}}}}\left({\frac {dr}{d\tau }}\right)^{2}-r^{2}\left({\frac {d\varphi }{d\tau }}\right)^{2},$

дает уравнение движения радиуса как функции собственного времени ${\textstyle \tau }$:

$\left({\frac {dr}{d\tau }}\right)^{2}={\frac {E^{2}}{m^{2}c^{2}}}-\left(1-{\frac {r_{\text{s}}}{r}}\right)\left(c^{2}+{\frac {h^{2}}{r^{2}}}\right).$

Формальное решение этой проблемы:

$\tau =\int {\frac {dr}{\pm {\sqrt {{\frac {E^{2}}{m^{2}c^{2}}}-\left(1-{\frac {r_{\text{s}}}{r}}\right)\left(c^{2}+{\frac {h^{2}}{r^{2}}}\right)}}}}.$

Обратите внимание, что квадратный корень для тахионных геодезических будет мнимым.

Используя вышеприведенное соотношение между ${\textstyle {\frac {dt}{d\tau }}}$ и ${\textstyle E}$, мы также можем написать

$t=\int {\frac {dr}{\pm c\left(1-{\frac {r_{\text{s}}}{r}}\right){\sqrt {1-\left(1-{\frac {r_{\text{s}}}{r}}\right)\left(c^{2}+{\frac {h^{2}}{r^{2}}}\right){\frac {m^{2}c^{2}}{E^{2}}}}}}}.$

Поскольку асимптотически подынтегральная функция обратно пропорциональна ${\textstyle r-r_{\text{s}}}$, это показывает, что в ${\textstyle r,\theta ,\varphi ,t}$ система отсчета, если ${\textstyle r}$ подходы ${\textstyle r_{\text{s}}}$ он делает это экспоненциально, даже не достигая этого. Однако в зависимости от ${\textstyle \tau }$, ${\textstyle r}$ достигает ${\textstyle r_{\text{s}}}$.

Вышеупомянутые решения действительны, пока подынтегральная функция конечна, но полное решение может включать в себя две или бесконечное количество частей, каждая из которых описывается интегралом, но с чередующимися знаками квадратного корня.

Когда ${\textstyle E=mc^{2}}$ и ${\textstyle h=0}$, мы можем решить ${\textstyle t}$ и ${\textstyle \tau }$ явно:

${\begin{aligned}t&={\text{constant}}\pm {\frac {r_{\text{s}}}{c}}\left({\frac {2}{3}}\left({\frac {r}{r_{\text{s}}}}\right)^{\frac {3}{2}}+2{\sqrt {\frac {r}{r_{\text{s}}}}}+\ln {\frac {\left|{\sqrt {\frac {r}{r_{\text{s}}}}}-1\right|}{{\sqrt {\frac {r}{r_{\text{s}}}}}+1}}\right)\\\tau &={\text{constant}}\pm {\frac {2}{3}}{\frac {r_{\text{s}}}{c}}\left({\frac {r}{r_{\text{s}}}}\right)^{\frac {3}{2}}\end{aligned}}$

и для фотонной геодезии ( ${\textstyle m=0}$) с нулевым угловым моментом

${\begin{aligned}t&={\text{constant}}\pm {\frac {1}{c}}\left(r+r_{\text{s}}\ln \left|{\frac {r}{r_{\text{s}}}}-1\right|\right)\\\tau &={\text{constant}}.\end{aligned}}$

(Хотя собственное время в фотонном случае тривиально, можно определить аффинный параметр ${\textstyle \lambda }$, и тогда решение уравнения геодезических будет ${\textstyle r=c_{1}\lambda +c_{2}}$.)

Другой разрешимый случай — это случай, когда ${\textstyle E=0}$ и ${\textstyle t}$ и ${\textstyle \varphi }$ постоянны. В томе, где ${\textstyle r<r_{\text{s}}}$ это дает в нужное время

$\tau ={\text{constant}}\pm {\frac {r_{\text{s}}}{c}}\left(\arcsin {\sqrt {\frac {r}{r_{\text{s}}}}}-{\sqrt {{\frac {r}{r_{\text{s}}}}\left(1-{\frac {r}{r_{\text{s}}}}\right)}}\right).$

Это близко к решениям с ${\textstyle {\frac {E^{2}}{m^{2}}}}$ маленький и позитивный. За пределами ${\textstyle r_{\text{s}}}$ тот ${\textstyle E=0}$ решение тахионное, а «собственное время» пространственноподобно:

$\tau ={\text{constant}}\pm i{\frac {r_{\text{s}}}{c}}\left(\ln \left({\sqrt {\frac {r}{r_{\text{s}}}}}+{\sqrt {{\frac {r}{r_{\text{s}}}}-1}}\right)+{\sqrt {{\frac {r}{r_{\text{s}}}}\left({\frac {r}{r_{\text{s}}}}-1\right)}}\right).$

Это близко к другим тахионным решениям с ${\textstyle {\frac {E^{2}}{m^{2}}}}$ маленький и отрицательный. Константа ${\textstyle t}$ тахионная геодезическая снаружи ${\textstyle r_{\text{s}}}$ не продолжается константой ${\textstyle t}$ геодезический внутри ${\textstyle r_{\text{s}}}$, а скорее продолжается в «параллельную внешнюю область» (см. координаты Крускала – Секереса ). Другие тахионные решения могут войти в черную дыру и выйти в параллельную внешнюю область. Константа ${\textstyle t}$ решение внутри горизонта событий ( ${\textstyle r_{\text{s}}}$) продолжается константой ${\textstyle t}$ Решение в белой дыре .

Когда угловой момент не равен нулю, мы можем заменить зависимость от собственного времени зависимостью от угла ${\textstyle \varphi }$ используя определение ${\textstyle h}$

$\left({\frac {dr}{d\varphi }}\right)^{2}=\left({\frac {dr}{d\tau }}\right)^{2}\left({\frac {d\tau }{d\varphi }}\right)^{2}=\left({\frac {dr}{d\tau }}\right)^{2}\left({\frac {r^{2}}{h}}\right)^{2},$

что дает уравнение для орбиты

$\left({\frac {dr}{d\varphi }}\right)^{2}={\frac {r^{4}}{b^{2}}}-\left(1-{\frac {r_{\text{s}}}{r}}\right)\left({\frac {r^{4}}{a^{2}}}+r^{2}\right)$

где для краткости две шкалы длин, ${\textstyle a}$ и ${\textstyle b}$, были определены

${\begin{aligned}a&={\frac {h}{c}},\\b&={\frac {cL}{E}}={\frac {hmc}{E}}.\end{aligned}}$

Отметим, что в тахионном случае ${\textstyle a}$ будет воображаемым и ${\textstyle b}$ реальный или бесконечный.

То же уравнение можно вывести, используя лагранжев подход. или уравнение Гамильтона – Якоби (см. ниже ). Решение уравнения орбиты есть

$\varphi =\int {\frac {dr}{\pm r^{2}{\sqrt {{\frac {1}{b^{2}}}-\left(1-{\frac {r_{\text{s}}}{r}}\right)\left({\frac {1}{a^{2}}}+{\frac {1}{r^{2}}}\right)}}}}.$

Это можно выразить через эллиптическую функцию Вейерштрасса ${\textstyle \wp }$.

Локальные и запаздывающие скорости

В отличие от классической механики, в координатах Шварцшильда ${\textstyle {\frac {{\rm {d}}r}{{\rm {d}}\tau }}}$ и ${\textstyle r\ {\frac {{\rm {d}}\varphi }{{\rm {d}}\tau }}}$ не являются радиальными ${\textstyle v_{\parallel }}$ и поперечный ${\textstyle v_{\perp }}$ компоненты местной скорости ${\textstyle v}$ (относительно неподвижного наблюдателя), вместо этого они дают компоненты скорости , связанные с ${\textstyle v}$ к

${\frac {{\rm {d}}r}{{\rm {d}}\tau }}=v_{\parallel }{\sqrt {1-{\frac {r_{\text{s}}}{r}}}}\ \gamma$

для радиального и

${\frac {{\rm {d}}\varphi }{{\rm {d}}\tau }}={\frac {v_{\perp }}{r}}\ \gamma$

для поперечной составляющей движения, при этом ${\textstyle v^{2}=v_{\parallel }^{2}+v_{\perp }^{2}}$. Координатный бухгалтер вдали от места происшествия наблюдает за задержкой по шапиро скорости. ${\textstyle {\hat {v}}}$, что определяется соотношением

${\hat {v}}_{\perp }=v_{\perp }{\sqrt {1-{\frac {r_{\text{s}}}{r}}}}$ и ${\hat {v}}_{\parallel }=v_{\parallel }\left(1-{\frac {r_{\text{s}}}{r}}\right)$.

Коэффициент замедления времени между бухгалтером и движущейся пробной частицей также можно представить в виде

${\frac {{\rm {d}}\tau }{{\rm {d}}t}}={\frac {\sqrt {1-{\frac {r_{\text{s}}}{r}}}}{\gamma }}$

где числитель — гравитационная, а знаменатель — кинематическая составляющая замедления времени. Для частицы, падающей из бесконечности, левый множитель равен правому множителю, поскольку скорость падения ${\textstyle v}$ соответствует скорости убегания ${\textstyle c{\sqrt {\frac {r_{\text{s}}}{r}}}}$ в этом случае.

Две константы углового момента ${\textstyle L}$ и полная энергия ${\textstyle E}$ пробной частицы с массой ${\textstyle m}$ с точки зрения ${\textstyle v}$

$L=m\ v_{\perp }\ r\ \gamma$

и

$E=mc^{2}\ {\sqrt {1-{\frac {r_{\text{s}}}{r}}}}\ \gamma$

где

$E=E_{\rm {rest}}+E_{\rm {kin}}+E_{\rm {pot}}$

и

$E_{\rm {rest}}=mc^{2}\ ,\ \ E_{\rm {kin}}=(\gamma -1)mc^{2}\ ,\ \ E_{\rm {pot}}=\left({\sqrt {1-{\frac {r_{\text{s}}}{r}}}}-1\right)\ \gamma \ mc^{2}$

Для массивных тестовых частиц ${\textstyle \gamma }$ это фактор Лоренца ${\textstyle \gamma =1/{\sqrt {1-v^{2}/c^{2}}}}$ и ${\textstyle \tau }$ — собственное время, а для безмассовых частиц, таких как фотоны ${\textstyle \gamma }$ установлено на ${\textstyle 1}$ и ${\textstyle \tau }$ играет роль аффинного параметра. Если частица безмассовая ${\textstyle E_{\rm {rest}}}$ заменяется на ${\textstyle E_{\rm {kin}}}$ и ${\textstyle mc^{2}}$ с ${\textstyle hf}$, где ${\textstyle h}$ Планка постоянная и ${\textstyle f}$ локально наблюдаемая частота.

Точное решение с использованием эллиптических функций

Основное уравнение орбиты легче решить если оно выражено через обратный радиус ${\textstyle u={\frac {1}{r}}}$

$\left({\frac {du}{d\varphi }}\right)^{2}={\frac {1}{b^{2}}}-\left(1-ur_{\text{s}}\right)\left({\frac {1}{a^{2}}}+u^{2}\right)$

Правая часть этого уравнения представляет собой кубический многочлен , имеющий три корня , обозначенный здесь как ${\textstyle u_{1}}$, ${\textstyle u_{2}}$, и ${\textstyle u_{3}}$

$\left({\frac {du}{d\varphi }}\right)^{2}=r_{\text{s}}\left(u-u_{1}\right)\left(u-u_{2}\right)\left(u-u_{3}\right)$

Сумма трех корней равна коэффициенту ${\textstyle u^{2}}$ срок

$u_{1}+u_{2}+u_{3}={\frac {1}{r_{\text{s}}}}$

Кубический многочлен с действительными коэффициентами может иметь либо три действительных корня, либо один действительный корень и два комплексно-сопряженных корня. Если все три корня — действительные числа , то корни помечаются так, что ${\textstyle u_{1}<u_{2}<u_{3}}$. Если вместо этого существует только один действительный корень, то это обозначается как ${\textstyle u_{3}}$; комплексно-сопряженные корни обозначены ${\textstyle u_{1}}$ и ${\textstyle u_{2}}$. Согласно правилу знаков Декарта , может быть не более одного отрицательного корня; ${\textstyle u_{1}}$ отрицательно тогда и только тогда, когда ${\textstyle b<a}$. Как обсуждается ниже, корни полезны при определении типов возможных орбит.

Учитывая такую ​​маркировку корней, решение фундаментального орбитального уравнения имеет вид

$u=u_{1}+\left(u_{2}-u_{1}\right)\,\mathrm {sn} ^{2}\left({\frac {1}{2}}\varphi {\sqrt {r_{\text{s}}\left(u_{3}-u_{1}\right)}}+\delta \right)$

где ${\textstyle \mathrm {sn} }$ представляет собой синусовую амплитудную функцию (одну из эллиптических функций Якоби ) и ${\textstyle \delta }$ – константа интегрирования, отражающая исходное положение. Эллиптический модуль ${\textstyle k}$ этой эллиптической функции задается формулой

$k={\sqrt {\frac {u_{2}-u_{1}}{u_{3}-u_{1}}}}$

Ньютоновский предел

Чтобы восстановить ньютоновское решение для планетарных орбит, за предел принимают радиус Шварцшильда. ${\textstyle r_{\text{s}}}$ уходит в ноль. В этом случае третий корень ${\textstyle u_{3}}$ становится примерно ${\textstyle {\frac {1}{r_{\text{s}}}}}$и намного больше, чем ${\textstyle u_{1}}$ или ${\textstyle u_{2}}$. Следовательно, модуль ${\textstyle k}$ стремится к нулю; в этом пределе, ${\textstyle \mathrm {sn} }$ становится тригонометрической синусоидальной функцией

$u=u_{1}+\left(u_{2}-u_{1}\right)\,\sin ^{2}\left({\frac {1}{2}}\varphi +\delta \right)$

В соответствии с решениями Ньютона для движения планет эта формула описывает фокальную конику эксцентриситета. ${\textstyle e}$

$e={\frac {u_{2}-u_{1}}{u_{2}+u_{1}}}$

Если ${\textstyle u_{1}}$ является положительным действительным числом, то орбита представляет собой эллипс , где ${\textstyle u_{1}}$ и ${\textstyle u_{2}}$ представляют собой расстояния самого дальнего и самого близкого сближения соответственно. Если ${\textstyle u_{1}}$ — ноль или отрицательное действительное число, орбита — парабола или гипербола соответственно. В этих последних двух случаях ${\textstyle u_{2}}$ представляет собой расстояние наибольшего сближения; так как орбита уходит в бесконечность ( ${\textstyle u=0}$), нет расстояния самого дальнего приближения.

Корни и обзор возможных орбит

Корень представляет собой точку орбиты, в которой производная обращается в нуль, т. е. где ${\textstyle {\frac {du}{d\phi }}=0}$. В такой поворотный момент, ${\textstyle u}$ достигает максимума, минимума или точки перегиба в зависимости от значения второй производной, которое определяется формулой

${\frac {d^{2}u}{d\varphi ^{2}}}={\frac {r_{\text{s}}}{2}}\left[\left(u-u_{2}\right)\left(u-u_{3}\right)+\left(u-u_{1}\right)\left(u-u_{3}\right)+\left(u-u_{1}\right)\left(u-u_{2}\right)\right]$

все три корня являются различными действительными числами, вторая производная положительна, отрицательна и положительна в , _u1 u2 и _Если u3 соответственно _точках . Отсюда следует, что график зависимости u от φ может либо колебаться между u ₁ и u ₂ , либо двигаться от u ₃ к бесконечности (что соответствует стремлению r к нулю). Если u ₁ отрицательно, фактически произойдет только часть «колебаний». Это соответствует частице, исходящей из бесконечности, приближающейся к центральной массе, а затем снова удаляющейся к бесконечности, как гиперболическая траектория в классическом решении.

Если частица имеет ровно столько энергии, сколько соответствует ее угловому моменту, u ₂ и u ₃ сольются. В этом случае есть три решения. Орбита может свернуть по спирали ${\textstyle r={\frac {1}{u_{2}}}={\frac {1}{u_{3}}}}$, приближаясь к этому радиусу как (асимптотически) к убывающей экспоненте по φ, ${\textstyle \tau }$, или ${\textstyle t}$. Или можно иметь круговую орбиту такого радиуса. Или можно иметь орбиту, спускающуюся по спирали от этого радиуса к центральной точке. Рассматриваемый радиус называется внутренним радиусом и находится между ${\textstyle {\frac {3}{2}}}$ и 3 раза р _с . Круговая орбита также возникает, когда ${\textstyle u_{2}}$ равно ${\textstyle u_{1}}$, и это называется внешним радиусом. Эти различные типы орбит обсуждаются ниже.

Если частица приближается к центральной массе с достаточной энергией и достаточно малым угловым моментом, то только ${\textstyle u_{1}}$ будет реальным. Это соответствует падению частицы в черную дыру. Орбита движется по спирали с конечным изменением φ.

Прецессия орбит

Функция sn и ее квадрат sn ² имеют периоды 4 К и 2 К соответственно, где К определяется уравнением

$K=\int _{0}^{1}{\frac {dy}{\sqrt {\left(1-y^{2}\right)\left(1-k^{2}y^{2}\right)}}}$

Следовательно, изменение φ за одно колебание ${\textstyle u}$ (или, что то же самое, одно колебание ${\textstyle r}$) равно

$\Delta \varphi ={\frac {4K}{\sqrt {r_{\text{s}}\left(u_{3}-u_{1}\right)}}}$

В классическом пределе u ₃ приближается ${\textstyle {\frac {1}{r_{\text{s}}}}}$ и намного больше, чем ${\textstyle u_{1}}$ или ${\textstyle u_{2}}$. Следовательно, ${\textstyle k^{2}}$ примерно

$k^{2}={\frac {u_{2}-u_{1}}{u_{3}-u_{1}}}\approx r_{\text{s}}\left(u_{2}-u_{1}\right)\ll 1$

По тем же причинам знаменатель Δφ примерно равен

${\frac {1}{\sqrt {r_{\text{s}}\left(u_{3}-u_{1}\right)}}}={\frac {1}{\sqrt {1-r_{\text{s}}\left(2u_{1}+u_{2}\right)}}}\approx 1+{\frac {1}{2}}r_{\text{s}}\left(2u_{1}+u_{2}\right)$

Поскольку модуль ${\textstyle k}$ близок к нулю, период K можно разложить по степеням ${\textstyle k}$; в низший порядок это разложение дает

$K\approx \int _{0}^{1}{\frac {dy}{\sqrt {1-y^{2}}}}\left(1+{\frac {1}{2}}k^{2}y^{2}\right)={\frac {\pi }{2}}\left(1+{\frac {k^{2}}{4}}\right)$

Подстановка этих приближений в формулу для Δφ дает формулу углового опережения на одно радиальное колебание.

$\delta \varphi =\Delta \varphi -2\pi \approx {\frac {3}{2}}\pi r_{\text{s}}\left(u_{1}+u_{2}\right)$

Для эллиптической орбиты ${\textstyle u_{1}}$ и ${\textstyle u_{2}}$ представляют собой обратные значения самого длинного и самого короткого расстояний соответственно. Их можно выразить через большую полуось эллипса. ${\textstyle A}$ и его орбитальный эксцентриситет ${\textstyle e}$,

${\begin{aligned}r_{\text{max}}&={\frac {1}{u_{1}}}=A(1+e)\\r_{\text{min}}&={\frac {1}{u_{2}}}=A(1-e)\end{aligned}}$

предоставление

$u_{1}+u_{2}={\frac {2}{A\left(1-e^{2}\right)}}$

Подставив определение ${\textstyle r_{\text{s}}}$ дает окончательное уравнение

$\delta \varphi \approx {\frac {6\pi GM}{c^{2}A\left(1-e^{2}\right)}}$

Искривление света под действием силы тяжести

См. Также: Гравитационная линза и задержка Шапиро.

Схема гравитационного линзирования компактным телом

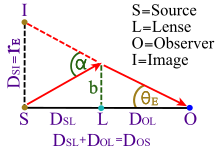
В пределе, когда масса частицы m стремится к нулю (или, что то же самое, если свет движется прямо к центральной массе, когда масштаб длины a стремится к бесконечности), уравнение орбиты принимает вид

$\varphi =\int {\frac {dr}{r^{2}{\sqrt {{\frac {1}{b^{2}}}-\left(1-{\frac {r_{\text{s}}}{r}}\right){\frac {1}{r^{2}}}}}}}$

Расширение полномочий ${\textstyle {\frac {r_{\text{s}}}{r}}}$, главный член этой формулы дает приблизительное угловое отклонение δ φ для безмассовой частицы, приходящей из бесконечности и возвращающейся обратно в бесконечность:

$\delta \varphi \approx {\frac {2r_{\text{s}}}{b}}={\frac {4GM}{c^{2}b}}.$

Здесь, ${\textstyle b}$ - прицельный параметр , несколько превышающий расстояние наибольшего сближения , ${\textstyle r_{3}}$:

$b=r_{3}{\sqrt {\frac {r_{3}}{r_{3}-r_{\text{s}}}}}$

Хотя эта формула приблизительна, она точна для большинства измерений гравитационного линзирования из-за малости отношения ${\textstyle {\frac {r_{\text{s}}}{r}}}$. Для света, падающего на поверхность Солнца, приблизительное угловое отклонение составляет примерно 1,75 угловых секунды , примерно одну миллионную часть окружности.

В более общем смысле, геодезические фотона, испускаемого источником света, расположенным в радиальной координате. $r={1 \over u}\in [r_{s},\infty [$ можно рассчитать следующим образом, применив уравнение

${\left({du \over d\varphi }\right)^{2}}=r_{s}\ u^{3}-u^{2}+{\frac {1}{b^{2}}}$

Геодезическая фотона, излучаемого источником света, расположенного на горизонте событий черной дыры и обратно к ней, с прицельным параметром $b>b_{crit}={\frac {3{\sqrt {3}}}{2}}r_{s}$.

Геодезическая фотона, испускаемого источником света, расположенным на горизонте событий черной дыры, с прицельным параметром $b=b_{crit}={\frac {3{\sqrt {3}}}{2}}r_{s}$ а затем переход на нестабильную орбиту $r_{crit}={3 \over 2}r_{s}$. Если $b<b_{crit}$ фотон высвобождается в бесконечность.

Уравнение можно вывести как

$2\ {\frac {du}{d\varphi }}{\frac {d^{2}u}{d\varphi ^{2}}}=3\ r_{s}u^{2}{\frac {du}{d\varphi }}-2\ u{\frac {du}{d\varphi }}$

что приводит к

${d^{2}u \over d\varphi ^{2}}={\frac {3}{2}}\ r_{s}\ u^{2}-\ u$

Это уравнение со второй производной можно численно проинтегрировать следующим образом с помощью 4 ^й заказать метод Рунге-Кутты, учитывая размер шага $\Delta \varphi$ и с:

$k_{1}={d^{2}u \over d\varphi ^{2}}(u)$,

$k_{2}={d^{2}u \over d\varphi ^{2}}{\bigl (}u+{\frac {\Delta \varphi }{2}}{du \over d\varphi }{\bigr )}$,

$k_{3}={d^{2}u \over d\varphi ^{2}}{\Bigl (}u+{\frac {\Delta \varphi }{2}}{du \over d\varphi }+{\frac {\Delta \varphi ^{2}}{4}}k_{1}{\Bigr )}$ и

$k_{4}={d^{2}u \over d\varphi ^{2}}{\Bigl (}u+\Delta \varphi {du \over d\varphi }+{\frac {\Delta \varphi ^{2}}{2}}k_{2}{\Bigr )}$.

Значение на следующем шаге ${du \over d\varphi }(\varphi +\Delta \varphi )$ является

${du \over d\varphi }(\varphi )+{\frac {\Delta \varphi }{6}}(k_{1}+2k_{2}+2k_{3}+k_{4})$

и значение на следующем шаге $u(\varphi +\Delta \varphi )$ является

$u(\varphi )+\Delta \varphi {du \over d\varphi }(\varphi )+{\frac {\Delta \varphi ^{2}}{6}}(k_{1}+k_{2}+k_{3})$

Шаг $\Delta \varphi$ может быть выбран постоянным или адаптивным, в зависимости от требуемой точности. $r={1 \over u}$.

Связь с ньютоновской физикой

Эффективная радиальная потенциальная энергия

Уравнение движения частицы, полученное выше

$\left({\frac {dr}{d\tau }}\right)^{2}={\frac {E^{2}}{m^{2}c^{2}}}-c^{2}+{\frac {r_{\text{s}}c^{2}}{r}}-{\frac {L^{2}}{m\mu r^{2}}}+{\frac {r_{\text{s}}L^{2}}{m\mu r^{3}}}$

можно переписать, используя определение радиуса Шварцшильда r _s, как

${\frac {1}{2}}m\left({\frac {dr}{d\tau }}\right)^{2}=\left[{\frac {E^{2}}{2mc^{2}}}-{\frac {1}{2}}mc^{2}\right]+{\frac {GMm}{r}}-{\frac {L^{2}}{2\mu r^{2}}}+{\frac {G(M+m)L^{2}}{c^{2}\mu r^{3}}},$

что эквивалентно движению частицы в одномерном эффективном потенциале

$V(r)=-{\frac {GMm}{r}}+{\frac {L^{2}}{2\mu r^{2}}}-{\frac {G(M+m)L^{2}}{c^{2}\mu r^{3}}}$

Первые два члена представляют собой хорошо известные классические энергии, первый из которых представляет собой притягивающую ньютоновскую гравитационную потенциальную энергию, а второй соответствует отталкивающей «центробежной» потенциальной энергии ; однако третий член представляет собой энергию притяжения, уникальную для общей теории относительности . Как показано ниже и в других местах , эта обратно-кубическая энергия заставляет эллиптические орбиты постепенно прецессировать на угол δφ за оборот.

$\delta \varphi \approx {\frac {6\pi G(M+m)}{c^{2}A\left(1-e^{2}\right)}}$

где ${\textstyle A}$ - большая полуось и ${\textstyle e}$ это эксцентриситет.

Третий член привлекателен и доминирует при малых ${\textstyle r}$ значения, определяющие критический внутренний радиус rinner _, при котором частица неумолимо втягивается внутрь к ${\textstyle r=0}$; этот внутренний радиус является функцией углового момента частицы на единицу массы или, что то же самое, ${\textstyle a}$ масштаб длины, определенный выше.

Круговые орбиты и их устойчивость

Эффективный радиальный потенциал для различных угловых моментов. На малых радиусах энергия резко падает, заставляя частицу неумолимо притягиваться внутрь, чтобы ${\textstyle r=0}$. Однако когда нормированный угловой момент ${\textstyle {\frac {a}{r_{\text{s}}}}={\frac {L}{mcr_{\text{s}}}}}$ равна квадратному корню из трех, метастабильная круговая орбита возможна на радиусе, выделенном зеленым кружком. При более высоких угловых моментах существует значительный центробежный барьер (оранжевая кривая) и нестабильный внутренний радиус, выделенный красным.

Эффективный потенциал ${\textstyle V}$ можно переписать через длину ${\textstyle a={\frac {h}{c}}}$.

$V(r)={\frac {\mu c^{2}}{2}}\left[-{\frac {r_{\text{s}}}{r}}+{\frac {a^{2}}{r^{2}}}-{\frac {r_{\text{s}}a^{2}}{r^{3}}}\right]$

Круговые орбиты возможны, когда эффективная сила равна нулю.

$F=-{\frac {dV}{dr}}=-{\frac {\mu c^{2}}{2r^{4}}}\left[r_{\text{s}}r^{2}-2a^{2}r+3r_{\text{s}}a^{2}\right]=0$

т. е. когда две силы притяжения — ньютоновская гравитация (первый член) и притяжение, уникальное для общей теории относительности (третий член), — точно уравновешиваются отталкивающей центробежной силой (второй член). Существует два радиуса, при которых может происходить такая балансировка, обозначенных здесь как r _{внутренний} и r _{внешний.}

${\begin{aligned}r_{\text{outer}}&={\frac {a^{2}}{r_{\text{s}}}}\left(1+{\sqrt {1-{\frac {3r_{\text{s}}^{2}}{a^{2}}}}}\right)\\[3pt]r_{\text{inner}}&={\frac {a^{2}}{r_{\text{s}}}}\left(1-{\sqrt {1-{\frac {3r_{\text{s}}^{2}}{a^{2}}}}}\right)={\frac {3a^{2}}{r_{\text{outer}}}}\end{aligned}}$

которые получаются по квадратичной формуле . Внутренний радиус rinner _{нестабилен} , потому что третья сила притяжения усиливается гораздо быстрее, чем две другие силы, когда r становится малым; если частица слегка скользит внутрь от r _{внутреннего} (где все три силы находятся в равновесии), третья сила доминирует над двумя другими и неумолимо тянет частицу внутрь до r = 0. Однако на внешнем радиусе круговые орбиты стабильны; третий член менее важен, и система ведет себя больше как нерелятивистская проблема Кеплера .

Когда ${\textstyle a}$ намного больше, чем ${\textstyle r_{\text{s}}}$ (классический случай) эти формулы принимают приближенный вид

${\begin{aligned}r_{\text{outer}}&\approx {\frac {2a^{2}}{r_{\text{s}}}}\\[3pt]r_{\text{inner}}&\approx {\frac {3}{2}}r_{\text{s}}\end{aligned}}$

Стабильный и нестабильный радиусы построены в зависимости от нормированного углового момента. ${\textstyle {\frac {a}{r_{\text{s}}}}={\frac {L}{mcr_{\text{s}}}}}$ синего и красного цвета соответственно. Эти кривые встречаются на уникальной круговой орбите (зеленый кружок), когда нормированный угловой момент равен квадратному корню из трех. Для сравнения классический радиус, предсказанный на основе центростремительного ускорения и закона гравитации Ньютона, показан черным цветом.

Подставляя определения ${\textstyle a}$ и r _s в r _{внешний} дает классическую формулу для частицы массы ${\textstyle m}$ вращающийся вокруг тела массы ${\textstyle M}$.

$r_{\mathrm {outer} }^{3}={\frac {G(M+m)}{\omega _{\varphi }^{2}}}$

где ω _φ — орбитальная угловая скорость частицы. Эта формула получается в нерелятивистской механике, если поставить центробежную силу равной ньютоновской силе гравитации:

${\frac {GMm}{r^{2}}}=\mu \omega _{\varphi }^{2}r$

Где ${\textstyle \mu }$ это приведенная масса .

В наших обозначениях классическая орбитальная угловая скорость равна

$\omega _{\varphi }^{2}\approx {\frac {GM}{r_{\mathrm {outer} }^{3}}}=\left({\frac {r_{\text{s}}c^{2}}{2r_{\mathrm {outer} }^{3}}}\right)=\left({\frac {r_{\text{s}}c^{2}}{2}}\right)\left({\frac {r_{\text{s}}^{3}}{8a^{6}}}\right)={\frac {c^{2}r_{\text{s}}^{4}}{16a^{6}}}$

Другая крайность, когда ² подходы 3 р _с ² сверху два радиуса сходятся к одному значению

$r_{\mathrm {outer} }\approx r_{\mathrm {inner} }\approx 3r_{\text{s}}$

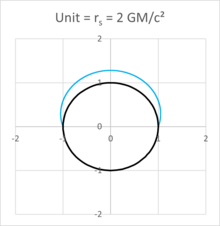
Квадратичные решения, приведенные выше, гарантируют, что r _external всегда больше 3 r _s , тогда как r _inner находится между 3 ⁄ 2   р _​ 3 р _. и Круговые орбиты меньше 3 ⁄ 2   р _. невозможны Для безмассовых частиц а стремится к бесконечности, подразумевая, что существует круговая орбита для фотонов при r _{внутренний} = 3 ⁄ 2   р _с . Сферу этого радиуса иногда называют фотонной сферой .

Прецессия эллиптических орбит

В нерелятивистской задаче Кеплера частица вечно движется по одному и тому же идеальному эллипсу (красной орбите). Общая теория относительности вводит третью силу, которая притягивает частицу немного сильнее, чем ньютоновская гравитация, особенно при малых радиусах. Эта третья сила заставляет эллиптическую орбиту частицы прецессировать ( голубая орбита) в направлении ее вращения; этот эффект был измерен на Меркурии , Венере и Земле. Желтая точка внутри орбит представляет центр притяжения, например Солнце .

Скорость орбитальной прецессии может быть получена с использованием этого радиального эффективного потенциала V . Небольшое радиальное отклонение от круговой орбиты радиуса r _{внешнего} будет стабильно колебаться с угловой частотой

$\omega _{r}^{2}={\frac {1}{m}}\left[{\frac {d^{2}V}{dr^{2}}}\right]_{r=r_{\mathrm {outer} }}$

что равно

$\omega _{r}^{2}=\left({\frac {c^{2}r_{\text{s}}}{2r_{\mathrm {outer} }^{4}}}\right)\left(r_{\mathrm {outer} }-r_{\mathrm {inner} }\right)=\omega _{\varphi }^{2}{\sqrt {1-{\frac {3r_{\text{s}}^{2}}{a^{2}}}}}$

Извлечение квадратного корня из обеих частей и выполнение разложения в ряд Тейлора дает результат.

$\omega _{r}=\omega _{\varphi }\left[1-{\frac {3r_{\text{s}}^{2}}{4a^{2}}}+{\mathcal {O}}\left({\frac {r_{\text{s}}^{4}}{a^{4}}}\right)\right]$

Умножение на период Т одного оборота дает прецессию орбиты за один оборот.

$\delta \varphi =T\left(\omega _{\varphi }-\omega _{r}\right)\approx 2\pi \left({\frac {3r_{\text{s}}^{2}}{4a^{2}}}\right)={\frac {3\pi m^{2}c^{2}}{2L^{2}}}r_{\text{s}}^{2}$

где мы использовали ω _φ T = 2 п и определение масштаба a . Подстановка определения радиуса Шварцшильда r _s дает

$\delta \varphi \approx {\frac {3\pi m^{2}c^{2}}{2L^{2}}}\left({\frac {4G^{2}M^{2}}{c^{4}}}\right)={\frac {6\pi G^{2}M^{2}m^{2}}{c^{2}L^{2}}}$

эллиптической орбиты Это можно упростить, используя полуось A и эксцентриситет e, связанные формулой

${\frac {h^{2}}{G(M+m)}}=A\left(1-e^{2}\right)$

чтобы задать угол прецессии

$\delta \varphi \approx {\frac {6\pi G(M+m)}{c^{2}A\left(1-e^{2}\right)}}$

Математический вывод орбитального уравнения

Символы Кристофера

Неисчезающие символы Кристоффеля для метрики Шварцшильда:

${\begin{aligned}\Gamma _{rt}^{t}=-\Gamma _{rr}^{r}&={\frac {r_{\text{s}}}{2r(r-r_{\text{s}})}}\\[3pt]\Gamma _{tt}^{r}&={\frac {r_{\text{s}}(r-r_{\text{s}})}{2r^{3}}}\\[3pt]\Gamma _{\phi \phi }^{r}&=(r_{\text{s}}-r)\sin ^{2}(\theta )\\[3pt]\Gamma _{\theta \theta }^{r}&=r_{\text{s}}-r\\[3pt]\Gamma _{r\theta }^{\theta }=\Gamma _{r\phi }^{\phi }&={\frac {1}{r}}\\[3pt]\Gamma _{\phi \phi }^{\theta }&=-\sin(\theta )\cos(\theta )\\[3pt]\Gamma _{\theta \phi }^{\phi }&=\cot(\theta )\end{aligned}}$

Геодезическое уравнение

Согласно общей теории относительности Эйнштейна, частицы незначительной массы перемещаются по геодезическим линиям в пространстве-времени. В плоском пространстве-времени, вдали от источника гравитации, эти геодезические соответствуют прямым линиям; однако они могут отклоняться от прямых линий, когда пространство-время искривлено. Уравнение геодезических линий имеет вид

${\frac {d^{2}x^{\lambda }}{dq^{2}}}+\Gamma _{\mu \nu }^{\lambda }{\frac {dx^{\mu }}{dq}}{\frac {dx^{\nu }}{dq}}=0$

где Γ представляет символ Кристоффеля и переменную ${\textstyle q}$ параметризует путь частицы в пространстве-времени , ее так называемую мировую линию . Символ Кристоффеля зависит только от метрического тензора ${\textstyle g_{\mu \nu }}$, или, скорее, от того, как оно меняется в зависимости от положения. Переменная ${\textstyle q}$ является постоянной кратной собственному времени ${\textstyle \tau }$ для времениподобных орбит (по которым перемещаются массивные частицы) и обычно принимается равным ему. Для светоподобных (или нулевых) орбит (по которым перемещаются безмассовые частицы, такие как фотон ) собственное время равно нулю и, строго говоря, не может использоваться в качестве переменной ${\textstyle q}$. Тем не менее, светоподобные орбиты можно вывести как ультрарелятивистский предел времениподобных орбит, то есть предел, при котором масса частицы m стремится к нулю при фиксированной ее полной энергии .

Следовательно, чтобы определить движение частицы, самым простым способом является решение уравнения геодезических - подход, принятый Эйнштейном. и другие. Метрику Шварцшильда можно записать как

$c^{2}d\tau ^{2}=w(r)c^{2}dt^{2}-v(r)dr^{2}-r^{2}d\theta ^{2}-r^{2}\sin ^{2}\theta d\phi ^{2}\,$

где две функции ${\textstyle w(r)=1-{\frac {r_{\text{s}}}{r}}}$и его взаимность ${\textstyle v(r)={\frac {1}{w(r)}}}$определены для краткости. Из этой метрики символы Кристоффеля ${\textstyle \Gamma _{\mu \nu }^{\lambda }}$можно рассчитать, а результаты подставить в уравнения геодезических

${\begin{aligned}0&={\frac {d^{2}\theta }{dq^{2}}}+{\frac {2}{r}}{\frac {d\theta }{dq}}{\frac {dr}{dq}}-\sin \theta \cos \theta \left({\frac {d\phi }{dq}}\right)^{2}\\[3pt]0&={\frac {d^{2}\phi }{dq^{2}}}+{\frac {2}{r}}{\frac {d\phi }{dq}}{\frac {dr}{dq}}+2\cot \theta {\frac {d\phi }{dq}}{\frac {d\theta }{dq}}\\[3pt]0&={\frac {d^{2}t}{dq^{2}}}+{\frac {1}{w}}{\frac {dw}{dr}}{\frac {dt}{dq}}{\frac {dr}{dq}}\\[3pt]0&={\frac {d^{2}r}{dq^{2}}}-{\frac {1}{v}}{\frac {dv}{dr}}\left({\frac {dr}{dq}}\right)^{2}-{\frac {r}{v}}\left({\frac {d\theta }{dq}}\right)^{2}-{\frac {r\sin ^{2}\theta }{v}}\left({\frac {d\phi }{dq}}\right)^{2}+{\frac {c^{2}}{2v}}{\frac {dw}{dr}}\left({\frac {dt}{dq}}\right)^{2}\end{aligned}}$

Можно убедиться, что ${\textstyle \theta ={\frac {\pi }{2}}}$ является допустимым решением путем подстановки в первое из этих четырех уравнений. По симметрии орбита должна быть плоской, и мы можем расположить систему координат так, чтобы экваториальная плоскость была плоскостью орбиты. Этот ${\textstyle \theta }$ Решение упрощает второе и четвертое уравнения.

Для решения второго и третьего уравнений достаточно разделить их на ${\textstyle {\frac {d\phi }{dq}}}$ и ${\textstyle {\frac {dt}{dq}}}$, соответственно.

${\begin{aligned}0&={\frac {d}{dq}}\left[\ln {\frac {d\phi }{dq}}+\ln r^{2}\right]\\[3pt]0&={\frac {d}{dq}}\left[\ln {\frac {dt}{dq}}+\ln w\right],\end{aligned}}$

что дает две константы движения.

Лагранжев подход

Поскольку пробные частицы следуют геодезическим линиям в фиксированной метрике, орбиты этих частиц можно определить с помощью вариационного исчисления, также называемого лагранжевым подходом. Геодезические в пространстве-времени определяются как кривые, для которых небольшие локальные изменения в их координатах (при фиксированных событиях в конечных точках) не приводят к существенному изменению их общей длины s . Это можно выразить математически с помощью вариационного исчисления.

$0=\delta s=\delta \int ds=\delta \int {\sqrt {g_{\mu \nu }{\frac {dx^{\mu }}{d\tau }}{\frac {dx^{\nu }}{d\tau }}}}d\tau =\delta \int {\sqrt {2T}}d\tau$

где τ — собственное время , s = cτ — длина дуги в пространстве-времени , а T определяется как

$2T=c^{2}=\left({\frac {ds}{d\tau }}\right)^{2}=g_{\mu \nu }{\frac {dx^{\mu }}{d\tau }}{\frac {dx^{\nu }}{d\tau }}=\left(1-{\frac {r_{\text{s}}}{r}}\right)c^{2}\left({\frac {dt}{d\tau }}\right)^{2}-{\frac {1}{1-{\frac {r_{\text{s}}}{r}}}}\left({\frac {dr}{d\tau }}\right)^{2}-r^{2}\left({\frac {d\varphi }{d\tau }}\right)^{2}$

по аналогии с кинетической энергией . Если производная по собственному времени для краткости обозначена точкой

${\dot {x}}^{\mu }={\frac {dx^{\mu }}{d\tau }}$

Т можно записать как

$2T=c^{2}=\left(1-{\frac {r_{\text{s}}}{r}}\right)c^{2}\left({\dot {t}}\right)^{2}-{\frac {1}{1-{\frac {r_{\text{s}}}{r}}}}\left({\dot {r}}\right)^{2}-r^{2}\left({\dot {\varphi }}\right)^{2}$

Постоянные факторы (такие как c или квадратный корень из двух) не влияют на ответ вариационной задачи; следовательно, взятие вариации внутри интеграла дает принцип Гамильтона

$0=\delta \int {\sqrt {2T}}d\tau =\int {\frac {\delta T}{\sqrt {2T}}}d\tau ={\frac {1}{c}}\delta \int Td\tau .$

Решение вариационной задачи дают уравнения Лагранжа

${\frac {d}{d\tau }}\left({\frac {\partial T}{\partial {\dot {x}}^{\sigma }}}\right)={\frac {\partial T}{\partial x^{\sigma }}}.$

Применительно к t и φ эти уравнения обнаруживают две константы движения:

${\begin{aligned}{\frac {d}{d\tau }}\left[r^{2}{\frac {d\varphi }{d\tau }}\right]&=0,\\{\frac {d}{d\tau }}\left[\left(1-{\frac {r_{\text{s}}}{r}}\right){\frac {dt}{d\tau }}\right]&=0,\end{aligned}}$

что может быть выражено через два постоянных масштаба длины, ${\textstyle a}$ и ${\textstyle b}$

${\begin{aligned}r^{2}{\frac {d\varphi }{d\tau }}&=ac,\\\left(1-{\frac {r_{\text{s}}}{r}}\right){\frac {dt}{d\tau }}&={\frac {a}{b}}.\end{aligned}}$

Как показано выше , подстановка этих уравнений в определение метрики Шварцшильда дает уравнение орбиты.

гамильтонов подход

Лагранжево решение можно преобразовать в эквивалентную гамильтонову форму. В этом случае гамильтониан $H$ дается

$2H=c^{2}={\frac {p_{t}^{2}}{c^{2}\left(1-{\frac {r_{\text{s}}}{r}}\right)}}-\left(1-{\frac {r_{\text{s}}}{r}}\right)p_{r}^{2}-{\frac {p_{\theta }^{2}}{r^{2}}}-{\frac {p_{\varphi }^{2}}{r^{2}\sin ^{2}\theta }}$

И снова орбита может быть ограничена ${\textstyle \theta ={\frac {\pi }{2}}}$по симметрии. С ${\textstyle t}$ и ${\textstyle \varphi }$ не появляются в гамильтониане, их сопряженные импульсы постоянны; их можно выразить через скорость света ${\textstyle c}$ и две постоянные шкалы длины ${\textstyle a}$ и ${\textstyle b}$

${\begin{aligned}p_{\varphi }&=-ac\\p_{\theta }&=0\\p_{t}&={\frac {ac^{2}}{b}}\end{aligned}}$

Производные по собственному времени имеют вид

${\begin{aligned}{\frac {dr}{d\tau }}&={\frac {\partial H}{\partial p_{r}}}=-\left(1-{\frac {r_{\text{s}}}{r}}\right)p_{r}\\{\frac {d\varphi }{d\tau }}&={\frac {\partial H}{\partial p_{\varphi }}}={\frac {-p_{\varphi }}{r^{2}}}={\frac {ac}{r^{2}}}\\{\frac {dt}{d\tau }}&={\frac {\partial H}{\partial p_{t}}}={\frac {p_{t}}{c^{2}\left(1-{\frac {r_{\text{s}}}{r}}\right)}}={\frac {a}{b\left(1-{\frac {r_{\text{s}}}{r}}\right)}}\end{aligned}}$

Разделив первое уравнение на второе, получим орбитальное уравнение

${\frac {dr}{d\varphi }}=-{\frac {r^{2}}{ac}}\left(1-{\frac {r_{\text{s}}}{r}}\right)p_{r}$

Радиальный импульс p _r можно выразить через r, используя постоянство гамильтониана ${\textstyle H={\frac {c^{2}}{2}}}$; это дает фундаментальное орбитальное уравнение

$\left({\frac {dr}{d\varphi }}\right)^{2}={\frac {r^{4}}{b^{2}}}-\left(1-{\frac {r_{\text{s}}}{r}}\right)\left({\frac {r^{4}}{a^{2}}}+r^{2}\right)$

Подход Гамильтона – Якоби

Искривление волн в гравитационном поле. Из-за гравитации время внизу течет медленнее, чем вверху, в результате чего волновые фронты (показаны черным) постепенно изгибаются вниз. Зеленая стрелка показывает направление кажущегося «гравитационного притяжения».

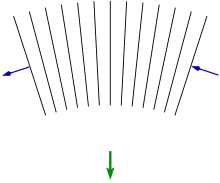
Орбитальное уравнение может быть получено из уравнения Гамильтона – Якоби . Преимущество этого подхода состоит в том, что он приравнивает движение частицы к распространению волны и аккуратно ведет к выводу отклонения света под действием гравитации в общей теории относительности через принцип Ферма . Основная идея заключается в том, что из-за гравитационного замедления времени части волнового фронта, расположенные ближе к гравитирующей массе, движутся медленнее, чем те, которые находятся дальше, изменяя таким образом направление распространения волнового фронта.

Используя общую ковариацию, уравнение Гамильтона – Якоби для одной частицы единичной массы можно выразить в произвольных координатах как

$g^{\mu \nu }{\frac {\partial S}{\partial x^{\mu }}}{\frac {\partial S}{\partial x^{\nu }}}=c^{2}.$

Это эквивалентно приведенной выше гамильтоновой формулировке, в которой частные производные действия заменяют обобщенные импульсы. Используя метрику Шварцшильда g ^{примечание} , это уравнение принимает вид

${\frac {1}{c^{2}\left(1-{\frac {r_{\text{s}}}{r}}\right)}}\left({\frac {\partial S}{\partial t}}\right)^{2}-\left(1-{\frac {r_{\text{s}}}{r}}\right)\left({\frac {\partial S}{\partial r}}\right)^{2}-{\frac {1}{r^{2}}}\left({\frac {\partial S}{\partial \varphi }}\right)^{2}=c^{2}$

где мы снова ориентируем сферическую систему координат с плоскостью орбиты. Время t и азимутальный угол φ являются циклическими координатами, так что решение для главной функции Гамильтона S можно записать

$S=-p_{t}t+p_{\varphi }\varphi +S_{r}(r)\,$

где $p_{t}$ и $p_{\varphi }$ — постоянные обобщенные импульсы. Уравнение Гамильтона–Якоби дает интегральное решение для радиальной части $S_{r}(r)$

$S_{r}(r)=\int ^{r}{\frac {dr}{1-{\frac {r_{\text{s}}}{r}}}}{\sqrt {{\frac {p_{t}^{2}}{c^{2}}}-\left(1-{\frac {r_{\text{s}}}{r}}\right)\left(c^{2}+{\frac {p_{\varphi }^{2}}{r^{2}}}\right)}}.$

Взяв производную главной функции Гамильтона S по сохраняющемуся импульсу p _φ, получим

${\frac {\partial S}{\partial p_{\varphi }}}=\varphi +{\frac {\partial S_{r}}{\partial p_{\varphi }}}=\mathrm {constant}$

что равно

$\varphi -\int ^{r}{\frac {p_{\varphi }dr}{r^{2}{\sqrt {{\frac {p_{t}^{2}}{c^{2}}}-\left(1-{\frac {r_{\text{s}}}{r}}\right)\left(c^{2}+{\frac {p_{\varphi }^{2}}{r^{2}}}\right)}}}}=\mathrm {constant}$

Если принять бесконечно малое изменение φ и r, получим фундаментальное орбитальное уравнение

$\left({\frac {dr}{d\varphi }}\right)^{2}={\frac {r^{4}}{b^{2}}}-\left(1-{\frac {r_{\text{s}}}{r}}\right)\left({\frac {r^{4}}{a^{2}}}+r^{2}\right).$

где сохраняющиеся масштабы длин a и b определяются сохраняющимися импульсами уравнениями

${\begin{aligned}{\frac {\partial S}{\partial \varphi }}=p_{\varphi }&=-ac\\{\frac {\partial S}{\partial t}}=p_{t}&={\frac {ac^{2}}{b}}\end{aligned}}$

Принцип Гамильтона

Интеграл действия для частицы, на которую действует только гравитация, равен

$S=\int {-mc^{2}d\tau }=-mc\int {c{\frac {d\tau }{dq}}dq}=-mc\int {{\sqrt {-g_{\mu \nu }{\frac {dx^{\mu }}{dq}}{\frac {dx^{\nu }}{dq}}}}dq}$

где ${\textstyle \tau }$ самое подходящее время и ${\textstyle q}$ — любая гладкая параметризация мировой линии частицы. Если применить к этому вариационное исчисление , то снова получим уравнения геодезической. Для упрощения вычислений сначала берут вариацию квадрата подынтегральной функции. Для метрики и координат этого случая и в предположении, что частица движется в экваториальной плоскости ${\textstyle \theta ={\frac {\pi }{2}}}$, этот квадрат

$\left(c{\frac {d\tau }{dq}}\right)^{2}=-g_{\mu \nu }{\frac {dx^{\mu }}{dq}}{\frac {dx^{\nu }}{dq}}=\left(1-{\frac {r_{\text{s}}}{r}}\right)c^{2}\left({\frac {dt}{dq}}\right)^{2}-{\frac {1}{1-{\frac {r_{\text{s}}}{r}}}}\left({\frac {dr}{dq}}\right)^{2}-r^{2}\left({\frac {d\varphi }{dq}}\right)^{2}\,.$

Вариация этого дает

$\delta \left(c{\frac {d\tau }{dq}}\right)^{2}=2c^{2}{\frac {d\tau }{dq}}\delta {\frac {d\tau }{dq}}=\delta \left[\left(1-{\frac {r_{\text{s}}}{r}}\right)c^{2}\left({\frac {dt}{dq}}\right)^{2}-{\frac {1}{1-{\frac {r_{\text{s}}}{r}}}}\left({\frac {dr}{dq}}\right)^{2}-r^{2}\left({\frac {d\varphi }{dq}}\right)^{2}\right]\,.$

Движение по долготе

Меняются по долготе ${\textstyle \varphi }$ только чтобы получить

$2c^{2}{\frac {d\tau }{dq}}\delta {\frac {d\tau }{dq}}=-2r^{2}{\frac {d\varphi }{dq}}\delta {\frac {d\varphi }{dq}}\,.$

Разделить на ${\textstyle 2c{\frac {d\tau }{dq}}}$ чтобы получить вариацию самого подынтегрального выражения

$c\,\delta {\frac {d\tau }{dq}}=-{\frac {r^{2}}{c}}{\frac {d\varphi }{d\tau }}\delta {\frac {d\varphi }{dq}}=-{\frac {r^{2}}{c}}{\frac {d\varphi }{d\tau }}{\frac {d\delta \varphi }{dq}}\,.$

Таким образом

$0=\delta \int {c{\frac {d\tau }{dq}}dq}=\int {c\delta {\frac {d\tau }{dq}}dq}=\int {-{\frac {r^{2}}{c}}{\frac {d\varphi }{d\tau }}{\frac {d\delta \varphi }{dq}}dq}\,.$

Интегрирование по частям дает

$0=-{\frac {r^{2}}{c}}{\frac {d\varphi }{d\tau }}\delta \varphi -\int {{\frac {d}{dq}}\left[-{\frac {r^{2}}{c}}{\frac {d\varphi }{d\tau }}\right]\delta \varphi dq}\,.$

Предполагается, что изменение долготы в конечных точках равно нулю, поэтому первый член исчезает. Интеграл можно сделать отличным от нуля ошибочным выбором ${\textstyle \delta \varphi }$ если только другой фактор внутри не равен нулю везде. Итак, уравнение движения

${\frac {d}{dq}}\left[-{\frac {r^{2}}{c}}{\frac {d\varphi }{d\tau }}\right]=0\,.$

Движение во времени

Меняться во времени ${\textstyle t}$ только чтобы получить

$2c^{2}{\frac {d\tau }{dq}}\delta {\frac {d\tau }{dq}}=2\left(1-{\frac {r_{\text{s}}}{r}}\right)c^{2}{\frac {dt}{dq}}\delta {\frac {dt}{dq}}\,.$

Разделить на ${\textstyle 2c{\frac {d\tau }{dq}}}$ чтобы получить вариацию самого подынтегрального выражения

$c\delta {\frac {d\tau }{dq}}=c\left(1-{\frac {r_{\text{s}}}{r}}\right){\frac {dt}{d\tau }}\delta {\frac {dt}{dq}}=c\left(1-{\frac {r_{\text{s}}}{r}}\right){\frac {dt}{d\tau }}{\frac {d\delta t}{dq}}\,.$

Таким образом

$0=\delta \int {c{\frac {d\tau }{dq}}dq}=\int {c\left(1-{\frac {r_{\text{s}}}{r}}\right){\frac {dt}{d\tau }}{\frac {d\delta t}{dq}}dq}\,.$

Интегрирование по частям дает

$0=c\left(1-{\frac {r_{\text{s}}}{r}}\right){\frac {dt}{d\tau }}\delta t-\int {{\frac {d}{dq}}\left[c\left(1-{\frac {r_{\text{s}}}{r}}\right){\frac {dt}{d\tau }}\right]\delta tdq}\,.$

Итак, уравнение движения

${\frac {d}{dq}}\left[c\left(1-{\frac {r_{\text{s}}}{r}}\right){\frac {dt}{d\tau }}\right]=0\,.$

Сохраняющиеся импульсы

Проинтегрируйте эти уравнения движения, чтобы определить константы интегрирования, получив

${\begin{aligned}L=p_{\phi }&=mr^{2}{\frac {d\varphi }{d\tau }}\,,\\E=-p_{t}&=mc^{2}\left(1-{\frac {r_{\text{s}}}{r}}\right){\frac {dt}{d\tau }}\,.\end{aligned}}$

Эти два уравнения для констант движения ${\textstyle L}$ (угловой момент) и ${\textstyle E}$ (энергию) можно объединить в одно уравнение, которое верно даже для фотонов и других безмассовых частиц, для которых собственное время вдоль геодезической равно нулю.

${\frac {d\varphi }{dt}}=\left(1-{\frac {r_{\text{s}}}{r}}\right){\frac {L\,c^{2}}{E\,r^{2}}}\,.$

Радиальное движение

Замена

${\frac {d\varphi }{d\tau }}={\frac {L}{m\,r^{2}}}\,$

и

${\frac {dt}{d\tau }}={\frac {E}{\left(1-{\frac {r_{\text{s}}}{r}}\right)m\,c^{2}}}\,$

в метрическое уравнение (и используя ${\textstyle \theta ={\frac {\pi }{2}}}$) дает

$c^{2}={\frac {1}{1-{\frac {r_{\text{s}}}{r}}}}\,{\frac {E^{2}}{m^{2}c^{2}}}-{\frac {1}{1-{\frac {r_{\text{s}}}{r}}}}\left({\frac {dr}{d\tau }}\right)^{2}-{\frac {1}{r^{2}}}\,{\frac {L^{2}}{m^{2}}}\,,$

из чего можно вывести

${\left({\frac {dr}{d\tau }}\right)}^{2}={\frac {E^{2}}{m^{2}c^{2}}}-\left(1-{\frac {r_{\text{s}}}{r}}\right)\left(c^{2}+{\frac {L^{2}}{m^{2}r^{2}}}\right)\,,$

что представляет собой уравнение движения для ${\textstyle r}$. Зависимость ${\textstyle r}$ на ${\textstyle \varphi }$ можно найти, разделив это на

${\left({\frac {d\varphi }{d\tau }}\right)}^{2}={\frac {L^{2}}{m^{2}r^{4}}}$

получить

${\left({\frac {dr}{d\varphi }}\right)}^{2}={\frac {E^{2}r^{4}}{L^{2}c^{2}}}-\left(1-{\frac {r_{\text{s}}}{r}}\right)\left({\frac {m^{2}c^{2}r^{4}}{L^{2}}}+r^{2}\right)\,$

что верно даже для частиц без массы. Если масштабы длины определяются

$a={\frac {L}{m\,c}}$

и

$b={\frac {L\,c}{E}}\,,$

тогда зависимость ${\textstyle r}$ на ${\textstyle \varphi }$ упрощается до

${\left({\frac {dr}{d\varphi }}\right)}^{2}={\frac {r^{4}}{b^{2}}}-\left(1-{\frac {r_{\text{s}}}{r}}\right)\left({\frac {r^{4}}{a^{2}}}+r^{2}\right)\,.$

См. также

• Классическая проблема центральной силы
• Поля кадра в общей теории относительности
• проблема Кеплера
• Задача двух тел в общей теории относительности

Библиография

• Шварцшильд, К. (1916). О гравитационном поле массовой точки по теории Эйнштейна. Труды Королевской прусской академии наук 1 , 189–196.
  • скан оригинальной бумаги
  • текст оригинальной статьи в Wikisource
  • перевод Анточи и Лойнгера
  • комментарий к статье, дающий более простой вывод
• Шварцшильд, К. (1916). О гравитационном поле сферы из несжимаемой жидкости. Труды Королевской прусской академии наук 1 , 424-?.
• Фламм, Л. (1916). «Вклад в теорию гравитации Эйнштейна». Физический журнал . 17 : 448–?.
• Адлер, Р; Базин М; Шиффер М. (1965). Введение в общую теорию относительности . Нью-Йорк: Книжная компания McGraw-Hill. стр. 177–193 . ISBN  978-0-07-000420-7 .
• Эйнштейн, А (1956). Значение теории относительности (5-е изд.). Принстон, Нью-Джерси: Издательство Принстонского университета. стр. 92–97 . ISBN  978-0-691-02352-6 .
• Хагихара, Ю (1931). «Теория релятивистских траекторий в гравитационном поле Шварцшильда». Японский журнал астрономии и геофизики . 8 : 67–176. Бибкод : 1931АОТок..31...67Н . ISSN   0368-346X .
• Ланчос, К. (1986). Вариационные принципы механики (4-е изд.). Нью-Йорк: Dover Publications. стр. 330–338. ISBN  978-0-486-65067-8 .
• Ландау, LD ; Лифшиц, Э.М. (1975). Классическая теория полей . Курс теоретической физики . Том. 2 (переработанное 4-е изд. на английском языке). Нью-Йорк: Пергамон Пресс. стр. 299–309. ISBN  978-0-08-018176-9 .
• Миснер, CW ; Торн, К. и Уилер, Дж. А. (1973). Гравитация . Сан-Франциско: WH Freeman. стр. Глава 25 (стр. 636–687), §33.5 (стр. 897–901) и §40.5 (стр. 1110–1116). ISBN  978-0-7167-0344-0 . (См. «Гравитация» (книга) .)
• Паис, А. (1982). Тонок Господь: Наука и жизнь Альберта Эйнштейна . Издательство Оксфордского университета. стр. 253–256 . ISBN  0-19-520438-7 .
• Паули, В. (1958). Теория относительности . Перевод Г. Филда. Нью-Йорк: Dover Publications. стр. 40–41 , 166–169. ISBN  978-0-486-64152-2 .
• Риндлер, В. (1977). Основная теория относительности: специальная, общая и космологическая (переработанное 2-е изд.). Нью-Йорк: Springer Verlag. стр. 143–149 . ISBN  978-0-387-10090-6 .
• Роузвир, Северная Каролина (1982). Перигелий Меркурия от Леверье до Эйнштейна . Оксфорд: Университетское издательство. ISBN  0-19-858174-2 .

• Синг, Дж. Л. (1960). Теория относительности: Общая теория . Амстердам: Издательство Северной Голландии. стр. 289–298 . ISBN  978-0-7204-0066-3 .
• Уолд, Р.М. (1984). Общая теория относительности . Чикаго: Издательство Чикагского университета. стр. 136–146 . ISBN  978-0-226-87032-8 .
• Уолтер, С. (2007). «Прорыв в 4-векторы: четырехмерное движение в гравитации, 1905–1910» . В Ренне, Дж. (ред.). Генезис общей теории относительности . Том. 3. Берлин: Шпрингер. стр. 193–252. Архивировано из оригинала 30 января 2009 г. Проверено 13 июля 2010 г.

• Вайнберг, С. (1972). Гравитация и космология . Нью-Йорк: Джон Уайли и сыновья. стр. 185–201 . ISBN  978-0-471-92567-5 .
• Уиттакер, ET (1937). Трактат об аналитической динамике частиц и твердых тел с введением в проблему трех тел (4-е изд.). Нью-Йорк: Dover Publications. стр. 389–393 . ISBN  978-1-114-28944-4 .

Внешние ссылки

• Отрывок из «Размышления об относительности» . книги Кевина Брауна