Правильная скорость

Не путать с правильным движением .

Логарифмический график зависимости γ (синий), v / c (голубой) и η (желтый) от собственной скорости w / c (т.е. импульса p / mc ). Обратите внимание, что w / c отслеживается по v / c на низких скоростях и по γ на высоких скоростях. Штриховая красная кривая — γ − 1 ( кинетическая энергия K / mc ² ), а пунктирная пурпурная кривая — релятивистский доплеровский фактор .

В относительности теории собственная скорость (также известная как скорость ) w объекта относительно наблюдателя представляет собой отношение вектора смещения , измеренного наблюдателем ${\textbf {x}}$ и собственное время τ, прошедшее на часах движущегося объекта:

${\textbf {w}}={\frac {d{\textbf {x}}}{d\tau }}$

Это альтернатива обычной скорости — расстоянию в единицу времени, при котором наблюдатель измеряет и расстояние, и время.

Два типа скорости, обычная и собственная, почти равны на низких скоростях. Однако при высоких скоростях собственная скорость сохраняет многие свойства, которые скорость теряет в теории относительности по сравнению с теорией Ньютона .Например, собственная скорость равна импульсу единицы массы при любой скорости и, следовательно, не имеет верхнего предела. На высоких скоростях, как показано на рисунке справа, она также пропорциональна энергии объекта.

Собственную скорость w можно связать с обычной скоростью v через фактор Лоренца γ :

${\textbf {w}}={\frac {d{\textbf {x}}}{dt}}{\frac {dt}{d\tau }}={\textbf {v}}\,\gamma (v)$

где t - координатное время или «время карты». движущегося объекта Для однонаправленного движения каждый из них также просто связан с углом гиперболической скорости или скоростью η соотношением

$\eta =\sinh ^{-1}{\frac {w}{c}}=\tanh ^{-1}{\frac {v}{c}}=\pm \cosh ^{-1}\gamma$.

Введение

В плоском пространстве-времени собственная скорость — это соотношение пройденного расстояния относительно рамки эталонной карты (используется для определения одновременности) и собственного времени τ, прошедшего на часах движущегося объекта. Он равен импульсу объекта p, разделенному на его массу покоя m , и состоит из пространственноподобных компонентов четырехвекторной скорости объекта . Уильяма Шерклиффа Монография упомянул его раннее использование в тексте Сирса и Бреме. Фраундорф исследовал его педагогическую ценность. в то время как Унгар, Бэйлис и лошади исследовали его актуальность с точки зрения теории групп и геометрической алгебры . Правильную скорость иногда называют стремительностью.

Крейсер выпадает из гиперпространства...

В отличие от более знакомой координатной скорости v , собственная скорость не синхронизирована. (не требует синхронизированных часов) и полезен для описания как суперрелятивистского, так и субрелятивистского движения. Подобно координатной скорости и в отличие от четырехвекторной скорости, она находится в трехмерном срезе пространства-времени, определенном фреймом карты. Как показано ниже и на рисунке справа, собственные скорости даже складываются в три вектора с изменением масштаба компонента вне кадра. Это делает их более полезными для картографических (например, инженерных) приложений и менее полезными для получения информации без координат. Собственная скорость, деленная на скорость света c, представляет собой гиперболический синус быстроты η , точно так же, как коэффициент Лоренца γ представляет собой гиперболический косинус быстроты, а координатная скорость v относительно скорости света представляет собой гиперболический тангенс быстроты.

Представьте себе объект, путешествующий через область пространства-времени, локально описываемую Германа Минковского метрическим уравнением плоского пространства ( cd τ ). ² = ( кд т) ² - ( d Икс ) ² . Здесь эталонная система координат и синхронизированные часы определяют положение карты x и время карты t соответственно, а d , предшествующий координате, означает бесконечно малое изменение. Небольшие манипуляции позволяют показать, что собственная скорость w = d x / d τ = γ v, где, как обычно, координатная скорость v = d x / dt . Таким образом, конечное значение w гарантирует, что v меньше скорости света c . Группируя γ с v в выражении для релятивистского импульса p , собственная скорость также расширяет ньютоновскую форму импульса как массу, умноженную на скорость, до высоких скоростей без необходимости использования релятивистской массы .

Правильная формула сложения скоростей

Правильная формула сложения скоростей:

$\mathbf {u} \oplus \mathbf {v} =\mathbf {u} +\mathbf {v} +\left\{{\frac {\beta _{\mathbf {u} }}{1+\beta _{\mathbf {u} }}}{\frac {\mathbf {u} \cdot \mathbf {v} }{c^{2}}}+{\frac {1-\beta _{\mathbf {v} }}{\beta _{\mathbf {v} }}}\right\}\mathbf {u}$

где $\beta _{\mathbf {w} }$ бета-фактор, определяемый выражением $\beta _{\mathbf {w} }={\frac {1}{\sqrt {1+{\frac {|\mathbf {w} |^{2}}{c^{2}}}}}}$.

Эта формула обеспечивает правильную пространства гировектора модель скорости гиперболической геометрии , которая использует все пространство по сравнению с другими моделями гиперболической геометрии, которые используют диски или полуплоскости.

В однонаправленном случае это становится коммутативным и упрощается до произведения фактора Лоренца, умноженного на сумму координатных скоростей, например, до w _AC = γ _AB γ _BC ( v _AB + v _BC ) , как обсуждается в разделе приложений ниже.

Связь с другими параметрами скорости

Таблица скоростей

Таблица ниже показывает, как собственная скорость w = c или «один картографический световой год на год путешествия» является естественным ориентиром для перехода от субрелятивистского движения к суперрелятивистскому.

Сравнение контрольных значений, нескольких вблизи релятивистского изменения наклона KE в зависимости от импульса.

Условие/Параметр	Координатная скорость v dx/dt в единицах c	Угол скорости η в я- радианах	Собственная скорость w dx / dτ в единицах c	Лоренц-фактор γ dt / dτ = E / mc 2
Путешественник остановился в рамке карты ⇔ 1 год карты/год путешественника	0	0	0	1
Импульс = ⁠ 1 / 2 ⁠ mc ⇔ 0,5 карто-светового года/год путешественника	1/ √ 5 ≅ 0.447	ln[(1 + √ 5 )/2] ≅ 0,481	⁠ 1 / 2 ⁠	√ 5 /2 ≅ 1.118
Скорость 0,5 гиперболического радиана.	( е - 1)/( е + 1) ≅ 0,462	⁠ 1 / 2 ⁠	⁠ 1 / 2 ⁠ ( √ e − 1/ √ e ) ≅ 0.521	⁠ 1 / 2 ⁠ ( √ e + 1/ √ e ) ≅ 1.128
Координатная скорость = ⁠ 1 / 2 ⁠ c ⇔ 0,5 карто-светового года/карто-года	⁠ 1 / 2 ⁠	⁠ 1 / 2 ⁠ ln[3] ≅ 0.549	1/ √ 3 ≅ 0.577	2/ √ 3 ≅ 1.155
Импульс = mc ⇔ 1 карта-световой год/год путешественника	1/ √ 2 ≅ 0.707	ln[1 + √ 2 ] ≅ 0,881	1	√ 2 ≅ 1.414
Скорость 1 гиперболический радиан	( и 2 − 1)/( и 2 + 1) ≅ 0.761	1	⁠ 1 / 2 ⁠ ( е - 1/ е ) ≅ 1,175	⁠ 1/2 ≅ ) ⁠ ( е + 1/ е 1,543
Кинетическая энергия = mc 2 ⇔ 2 карто-года/год путешественника	√ 3 /2 ≅ 0.866	ln[ √ 3 + 2] ≅ 1,317	√ 3 ≅ 1.732	2
Импульс = 2 мс ⇔ 2 карты-световых года/год путешественника	2/ √ 5 ≅ 0.894	ln[2 + √ 5 ] ≅ 1,444	2	√ 5 ≅ 2.236
Скорость 2 гиперболических радиана	( и 4 −1)/( и 4 +1) ≅ 0.964	2	⁠ 1/2 ​ ⁠ ​ ( и 2 − 1/ и 2 ) ≅ 3.627	⁠ 1/2 ​ ⁠ ​ ( и 2 + 1/ и 2 ) ≅ 3.762
Координатная скорость = c ⇔ 1 карто-световой год/карто-год	1	∞	∞	∞

Обратите внимание, что угол скорости η и собственная скорость w изменяются от 0 до бесконечности и отслеживают координатную скорость, когда w << c . С другой стороны, когда w >> c , собственная скорость соответствует коэффициенту Лоренца, тогда как угол скорости логарифмический и, следовательно, увеличивается гораздо медленнее.

Уравнения взаимного преобразования

Следующие уравнения преобразуют четыре альтернативные меры скорости (или однонаправленной скорости), которые вытекают из метрического уравнения Минковского для плоского пространства:

$(c\delta \tau )^{2}=(c\delta t)^{2}-(\delta x)^{2}.\,$.

Фактор Лоренца γ: энергия по mc ² ≥ 1

$\gamma \equiv {\frac {dt}{d\tau }}={\sqrt {1+\left({\frac {w}{c}}\right)^{2}}}={\frac {1}{\sqrt {1-({\frac {v}{c}})^{2}}}}=\cosh(\eta )\equiv {\frac {e^{\eta }+e^{-\eta }}{2}}$

Собственная скорость w : импульс на единицу массы.

${\frac {w}{c}}\equiv {\frac {1}{c}}{\frac {dx}{d\tau }}={\frac {v}{c}}{\frac {1}{\sqrt {1-({\frac {v}{c}})^{2}}}}=\sinh(\eta )\equiv {\frac {e^{\eta }-e^{-\eta }}{2}}=\pm {\sqrt {\gamma ^{2}-1}}$

Координатная скорость: v ≤ c

${\frac {v}{c}}\equiv {\frac {1}{c}}{\frac {dx}{dt}}={\frac {w}{c}}{\frac {1}{\sqrt {1+({\frac {w}{c}})^{2}}}}=\tanh(\eta )\equiv {\frac {e^{2\eta }-1}{e^{2\eta }+1}}=\pm {\sqrt {1-\left({\frac {1}{\gamma }}\right)^{2}}}$

Гиперболический угол скорости или быстрота

$\eta =\sinh ^{-1}\left({\frac {w}{c}}\right)=\tanh ^{-1}\left({\frac {v}{c}}\right)=\pm \cosh ^{-1}\left(\gamma \right)$

или в логарифмах:

$\eta =\ln \left({\frac {w}{c}}+{\sqrt {\left({\frac {w}{c}}\right)^{2}+1}}\right)={\frac {1}{2}}\ln \left({\frac {1+{\frac {v}{c}}}{1-{\frac {v}{c}}}}\right)=\pm \ln \left(\gamma +{\sqrt {\gamma ^{2}-1}}\right)$.

Приложения

Сравнение скоростей на высокой скорости.

Однонаправленное сложение скоростей: правильная сумма изгибается вверх.

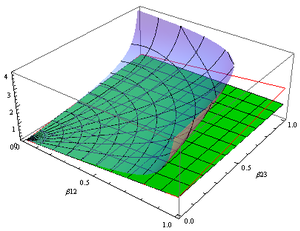
Правильная скорость полезна для сравнения скорости объектов с импульсом на единицу массы покоя ( w ), превышающим скорость света c . Координатная скорость таких объектов обычно близка к скорости света, тогда как собственная скорость показывает, насколько быстро они преодолевают землю по часам движущихся объектов . Это важно, например, если, подобно некоторым частицам космических лучей, движущиеся объекты имеют ограниченное время жизни. Правильная скорость также подсказывает нам импульс объекта, который не имеет верхней границы.

Например, электрон с энергией 45 ГэВ, ускоренный Большим электрон-позитронным коллайдером (LEP) в ЦЕРН в 1989 году, имел бы фактор Лоренца γ около 88 000 (45 ГэВ, разделенный на массу покоя электрона 511 кэВ). Его координатная скорость v была бы примерно на шестьдесят четыре триллионных долей скорости света c (1 световая секунда на секунду карты ). С другой стороны, его собственная скорость составляла бы w = γv ~ 88 000 световых секунд на секунду путешественника . Для сравнения: координатная скорость электрона с энергией 250 ГэВ в предлагаемом Международном линейном коллайдере. (ILC) останется около c , а ее собственная скорость значительно увеличится до ~489 000 световых секунд на секунду путешественника.

Правильная скорость также полезна для сравнения относительных скоростей вдоль линии на высокой скорости. В этом случае

${\frac {p_{AC}}{m_{1}}}=w_{AC}=\gamma _{AC}v_{AC}=\gamma _{AB}\gamma _{BC}\left(v_{AB}+v_{BC}\right)=\gamma _{AB}w_{BC}+w_{AB}\gamma _{BC}\,$

где A, B и C относятся к разным объектам или системам отсчета. Например, w _AC относится к правильной скорости объекта A относительно объекта C. Таким образом, при вычислении относительной собственной скорости коэффициенты Лоренца умножаются при суммировании координатных скоростей.

Следовательно, каждый из двух электронов (A и C) при лобовом столкновении при энергии 45 ГэВ в лабораторной системе координат (B) увидит, как другой приближается к ним при v _AC ~ c и w _AC = 88 000. ² (1 + 1) ~ 1.55×10 ¹⁰ световых секунд на секунду путешественника. Таким образом, с точки зрения цели, коллайдеры могут исследовать столкновения с гораздо более высокой энергией и импульсом снаряда на единицу массы.

Правильные дисперсионные соотношения на основе скорости

Графики ( γ − 1) c ² × масса в зависимости от собственной скорости × массы для диапазона значений массы вдоль обеих осей.

График зависимости «( γ − 1) от собственной скорости» после умножения первой на mc ² а последний по массе m для различных значений m дает семейство кривых зависимости кинетической энергии от импульса, которое включает большинство движущихся объектов, встречающихся в повседневной жизни. Такие графики можно, например, использовать, чтобы показать, где скорость света, постоянная Планка и энергия Больцмана kT фигурируют .

Для иллюстрации на рисунке справа с логарифмическими осями показаны объекты с одинаковой кинетической энергией (относящиеся по горизонтали), которые несут разное количество импульса, а также то, как скорость объекта малой массы сравнивается (путем вертикальной экстраполяции) со скоростью скорость после совершенно неупругого столкновения с покоящимся крупным объектом. Линии с сильным наклоном (подъем/пробег = 2) обозначают контуры постоянной массы, а линии с единичным наклоном обозначают контуры постоянной скорости.

Объекты, которые хорошо вписываются в этот сюжет, — это люди, управляющие автомобилями, частицы пыли в броуновском движении , космический корабль на орбите вокруг Солнца, молекулы при комнатной температуре, истребитель со скоростью 3 Маха, один радиоволновой фотон , человек, движущийся со скоростью один световой год в год. год путешественника, импульс лазера мощностью 1,8 мегаджоуля , электрон с энергией 250 ГэВ и наша наблюдаемая Вселенная с кинетической энергией черного тела, ожидаемой от одиночной частицы при температуре 3 кельвина.

Однонаправленное ускорение за счет правильной скорости

Правильное ускорение на любой скорости — это физическое ускорение, испытываемое объектом локально . В пространстве-времени это трехвекторное ускорение по отношению к мгновенно меняющейся системе координат свободного плавания объекта. этого объекта Его величина α — это инвариантная к кадру величина четырехкратного ускорения . Правильное ускорение также полезно с точки зрения (или среза пространства-времени) внешних наблюдателей. Наблюдатели во всех кадрах не только могут прийти к единому мнению относительно его величины, но он также измеряет степень, в которой ускоряющаяся ракета «вжимает педаль в пол».

В однонаправленном случае, т. е. когда ускорение объекта параллельно или антипараллельно его скорости в пространственно-временном срезе наблюдателя, изменение собственной скорости представляет собой интеграл от собственного ускорения по времени отображения, т. е. Δ w = α Δ t для постоянного α . На низких скоростях это сводится к хорошо известному соотношению между координатной скоростью и ускорения временем отображения времени координат, т.е. Δ v = a Δ t . Для постоянного однонаправленного собственного ускорения аналогичные зависимости существуют между быстротой η и затраченным собственным временем Δ τ , а также между фактором Лоренца γ и пройденным расстоянием Δ x . Чтобы быть конкретным:

$\alpha ={\frac {\Delta w}{\Delta t}}=c{\frac {\Delta \eta }{\Delta \tau }}=c^{2}{\frac {\Delta \gamma }{\Delta x}}$,

где, как отмечалось выше, различные параметры скорости связаны соотношением

$\eta =\sinh ^{-1}\left({\frac {w}{c}}\right)=\tanh ^{-1}\left({\frac {v}{c}}\right)=\pm \cosh ^{-1}\left(\gamma \right)$.

Эти уравнения описывают некоторые последствия ускоренного движения на высокой скорости. Например, представьте себе космический корабль, который может ускорять своих пассажиров на 1 g (или 1,03 светового года в год). ² ) на полпути к месту назначения, а затем замедлите их на 1 g на оставшуюся половину, чтобы обеспечить искусственную гравитацию земного типа из точки A в точку B за максимально короткое время. Для расстояния по карте Δx _AB первое уравнение, приведенное выше, предсказывает коэффициент Лоренца в средней точке (вверх от ее единичного значения покоя) γmid ₌ 1+α(Δx _AB /2)/c ² . Следовательно, время прохождения туда и обратно на путевых часах будет Δτ = 4(c/α)cosh. ⁻¹ [γmid _] , в течение которого время, прошедшее на часах карты, будет Δt = 4(c/α)sinh[cosh ⁻¹ [γ _{середина} ]].

График параметров скорости и времени на горизонтальной оси в зависимости от положения на вертикальной оси для ускоренного двойного полета туда и обратно до пункта назначения с Δx _AB = 10c. ² /α ~10 световых лет, если α~9,8 м/с. ² .

Этот воображаемый космический корабль мог бы совершать полеты к Проксиме Центавра туда и обратно продолжительностью около 7,1 лет (около 12 лет по земным часам), путешествия туда и обратно к Млечного Пути центральной черной дыре продолжительностью около 40 лет (прошло около 54 000 лет по земным часам) и Путешествие туда и обратно к Галактике Андромеды продолжительностью около 57 лет (более 5 миллионов лет по земным часам). К сожалению, хотя ускорение ракеты в 1 g может быть легко достигнуто, оно не может поддерживаться в течение длительного периода времени.

См. также

• Кинематика : для изучения способов изменения положения со временем.
• Фактор Лоренца : γ = dt / d τ или кинетическая энергия по mc. ²
• Быстрота : угол гиперболической скорости в мнимых радианах.
• Четыре скорости : объединение путешествий во времени и пространстве.
• Равномерное ускорение : фиксированное ускорение координат.
• Координаты Гулстранда – Пенлеве : свободно плавающие рамки в искривленном пространстве-времени.

Внешние ссылки

• Физика пространства-времени Эдвина Ф. Тейлора и Джона Арчибальда Уиллера