Координаты Гулстранд – Пенлеве

Координаты Гулстранда – Пенлеве представляют собой особый набор координат для метрики Шварцшильда – решения уравнений поля Эйнштейна , которое описывает черную дыру . Входные координаты таковы, что временная координата соответствует собственному времени свободно падающего наблюдателя, который стартует издалека с нулевой скоростью, а пространственные срезы плоские. На радиусе Шварцшильда (горизонте событий) сингулярности координат нет. Исходящие — это просто время, обратное входящим координатам (время — это собственное время вдоль исходящих частиц, которые достигают бесконечности с нулевой скоростью).

Решение было независимо предложено Полем Пенлеве в 1921 году. и Аллвар Галлстранд было явно показано, что эти решения были просто координатными преобразованиями обычного решения Шварцшильда : не в 1922 году. До 1933 года в статье Леметра хотя Эйнштейн сразу поверил, что это правда.

Вывод

Получение координат GP требует определения следующих систем координат и понимания того, как данные, измеренные для событий в одной системе координат, интерпретируются в другой системе координат.

Соглашение: все единицы измерения геометризированы . Время и масса имеют единицы измерения в метрах. Скорость света в плоском пространстве-времени имеет значение 1. Гравитационная постоянная имеет значение 1. Метрика выражается в соглашении о знаках +--- .

Координаты Шварцшильда

Свободнопадающие мировые линии в классических координатах Шварцшильда-Дросте

Наблюдатель Шварцшильда — это дальний наблюдатель или бухгалтер. Он не производит непосредственно измерений событий, происходящих в разных местах. Вместо этого он находится далеко от черной дыры и событий. Для проведения измерений и отправки ему результатов привлекаются местные наблюдатели. Бухгалтер собирает и объединяет отчеты из разных мест. Цифры в отчетах переводятся в данные в координатах Шварцшильда, которые обеспечивают систематические средства оценки и описания событий в глобальном масштабе. Таким образом, физик может разумно сравнивать и интерпретировать данные. Он может найти значимую информацию из этих данных. Шварцшильдовая форма метрики Шварцшильда с использованием координат Шварцшильда имеет вид

$g=\left(1-{\frac {2M}{r}}\right)\,dt^{2}-{\frac {dr^{2}}{\left(1-{\frac {2M}{r}}\right)}}-r^{2}\,d\theta ^{2}-r^{2}\sin ^{2}\theta \,d\phi ^{2}\,$

где

Г=1=с

t , r , θ , φ — координаты Шварцшильда,

М — масса черной дыры.

Координаты терапевта

Мировые линии свободного падения в координатах капли дождя Гулстранда – Пенлеве

Определите новую координату времени с помощью

$t_{r}=t+a(r)$

для некоторой произвольной функции $a(r)$. Подставляя в метрику Шварцшильда, получаем

$g=\left(1-{\frac {2M}{r}}\right)\,dt_{r}^{2}+2\left(1-{\frac {2M}{r}}\right)\,a'dt_{r}dr-\left({\frac {1}{1-{\frac {2M}{r}}}}-\left(1-{\frac {2M}{r}}\right)\,{a'}^{2}\right)dr^{2}-r^{2}\,d\theta ^{2}-r^{2}\sin ^{2}\theta \,d\phi ^{2}\,$

где $a'(r)={\frac {da}{dr}}$. Если мы сейчас выберем $a(r)$ такой, что член, умножающий $dr^{2}$ есть единица, мы получаем

$a'=-{\frac {1}{1-{\frac {2M}{r}}}}{\sqrt {\frac {2M}{r}}}$

и метрика становится

$g=\left(1-{\frac {2M}{r}}\right)\,dt_{r}^{2}-2{\sqrt {\frac {2M}{r}}}dt_{r}dr-dr^{2}-r^{2}\,d\theta ^{2}-r^{2}\sin ^{2}\theta \,d\phi ^{2}\,$

Пространственная метрика (т.е. ограничение метрики $g|_{t=t_{r}}$ на поверхности, где $t_{r}$ постоянна) — это просто плоская метрика, выраженная в сферических полярных координатах. Эта метрика является регулярной вдоль горизонта, где r=2M , поскольку, хотя временной член стремится к нулю, недиагональный член в метрике все еще отличен от нуля и гарантирует, что метрика по-прежнему обратима (определитель метрики равен $-r^{4}\sin(\theta )^{2}$).

Функция $a(r)$ дается

$a(r)=-\int {\frac {\sqrt {\frac {2M}{r}}}{1-{\frac {2M}{r}}}}dr=2M\left(-2y+\ln \left({\frac {y+1}{y-1}}\right)\right)$

где $y={\sqrt {\frac {r}{2M}}}$. Функция $a(r)$ явно сингулярна при r = 2M, поскольку так должно быть, если убрать эту сингулярность в метрике Шварцшильда.

Другие варианты для $a(r)$ привести к другим картам координат вакуума Шварцшильда; общее лечение проводится у Фрэнсиса и Косовского.

Движение капли дождя

Определите каплю дождя как объект, который падает радиально к черной дыре из состояния покоя на бесконечности.

В координатах Шварцшильда скорость капли дождя определяется выражением

${\frac {dr}{dt}}=-\left(1-{\frac {2M}{r}}\right){\sqrt {\frac {2M}{r}}}.\,$

• Скорость стремится к 0 по мере приближения r к горизонту событий. Капля дождя, похоже, замедлилась по мере приближения к горизонту событий и остановилась на горизонте событий, как показал бухгалтер. Действительно, наблюдатель за горизонтом событий увидел бы, как капля дождя падает все медленнее и медленнее. Его изображение бесконечно смещается в красную сторону и никогда не пересекает горизонт событий. Однако бухгалтер физически не измеряет скорость напрямую. Он переводит данные, передаваемые наблюдателем оболочки, в значения Шварцшильда и вычисляет скорость. Результатом является только бухгалтерская проводка.

В координатах GP скорость определяется выражением

${\frac {dr}{dt_{r}}}=-\beta =-{\sqrt {\frac {2M}{r}}}.\,$

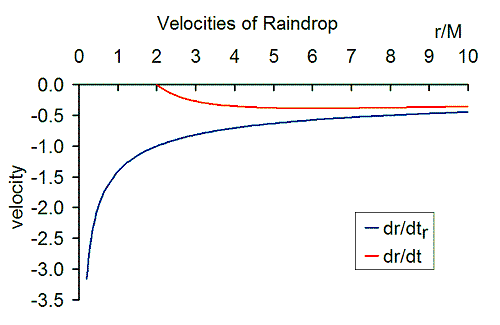
• Скорость дождевой капли обратно пропорциональна квадратному корню из радиуса и равна отрицательной ньютоновской скорости убегания . В точках, очень удаленных от черной дыры, скорость чрезвычайно мала. Когда капля дождя падает к черной дыре, скорость увеличивается. На горизонте событий скорость имеет значение 1. На горизонте событий нет разрыва или сингулярности.
• Внутри горизонта событий, $r<2M\,\!$ скорость увеличивается по мере приближения капли дождя к сингулярности. В конце концов, скорость становится бесконечной в сингулярности. Как показано ниже, скорость всегда меньше скорости света. Результаты не могут быть правильно предсказаны уравнением в сингулярности и очень близко к ней, поскольку истинное решение может быть совершенно другим, если включить квантовую механику.
• Несмотря на проблему с сингулярностью, все еще возможно математически вычислить время путешествия капли дождя от горизонта до центра черной дыры.

Интегрируем уравнение движения:

$\int _{0}^{T_{r}}\,dt=-\int _{2M}^{0}\left({\sqrt {\frac {2M}{r}}}\right)^{-1}\,dr.\,$ Результат $T_{r}={\frac {4}{3}}M.\,$

Используя этот результат для скорости капли дождя, мы можем найти собственное время на траектории капли дождя через время $t_{r}$. У нас есть

$d\tau ^{2}=g|_{\text{trajectory}}=dt_{r}^{2}\left[1-{\frac {2M}{r}}+2{\sqrt {\frac {2M}{r}}}{\sqrt {\frac {2M}{r}}}-{\sqrt {\frac {2M}{r}}}^{2}\right]=dt_{r}^{2}$

Т.е. по траектории капель дождя, по времени $t_{r}$ это в точности собственное время на траектории. Можно было бы определить координаты ВП исходя из этого требования, а не требуя, чтобы пространственные поверхности были плоскими.

Близкий набор координат — это координаты Леметра , в которых «радиальная» координата выбрана постоянной на пути капель дождя. Поскольку r изменяется по мере падения капель дождя, эта метрика зависит от времени, тогда как метрика GP не зависит от времени.

Метрика, полученная, если в приведенном выше примере мы возьмем функцию f (r) отрицательной по сравнению с тем, что мы выбрали выше, также называется системой координат GP. Единственное изменение в метрике заключается в том, что перекрестный член меняет знак. Эта метрика является регулярной для исходящих капель дождя, то есть частиц, которые покидают черную дыру и летят наружу со скоростью, достаточной для убегания, так что их скорость на бесконечности равна нулю. В обычных координатах ГП такие частицы невозможно описать при r<2M . Они имеют нулевое значение для ${\frac {dr}{dt_{r}}}$ при г=2М . Это указывает на то, что черная дыра Шварцшильда имеет два горизонта: горизонт прошлого и горизонт будущего. Исходная форма координат GP является регулярной на горизонте будущего (куда попадают частицы, когда они падают в черную дыру), тогда как альтернативная отрицательная версия является регулярной на горизонте прошлого (из которого частицы выходят из черной дыры, если они это делают). так).

Координаты Крускала – Секереса являются регулярными на обоих горизонтах за счет того, что метрика сильно зависит от временной координаты.

Скорость света

Предположим радиальное движение. Для света, $d\tau =0.$ Поэтому,

$0=\left(dr+\left(1+{\sqrt {\frac {2M}{r}}}\ \right)dt_{r}\right)\left(dr-\left(1-{\sqrt {\frac {2M}{r}}}\ \right)\,dt_{r}\right),$

${\frac {dr}{dt_{r}}}=\pm 1-{\sqrt {\frac {2M}{r}}}.$

• В местах, очень далеких от черной дыры, $r\to \infty ,{\tfrac {dr}{dt_{r}}}=\pm 1.$ Скорость света равна 1, как и в специальной теории относительности.
• На горизонте событий, $r=2M,$ Скорость света, исходящего из центра черной дыры, равна ${\tfrac {dr}{dt_{r}}}=0.$ Оно не может уйти за горизонт событий. Вместо этого он застревает на горизонте событий. Поскольку свет движется быстрее всех остальных, материя может двигаться только внутрь, к горизонту событий. Все, что находится внутри горизонта событий, скрыто от внешнего мира.
• Внутри горизонта событий, $r<2M,$ наблюдатель за дождем измеряет, что свет движется к центру со скоростью, большей 2. Это правдоподобно. Даже в специальной теории относительности собственная скорость движущегося объекта равна

  ${\frac {dr_{ff}}{d\tau }}={\frac {v}{\sqrt {1-v^{2}}}}\geq 1.$

Есть два важных момента, которые следует учитывать:

1. Ни один объект не должен иметь скорость, превышающую скорость света, измеренную в той же системе отсчета. Таким образом, принцип причинности сохраняется. Действительно, скорость капли дождя меньше скорости света: ${\frac {\left({\dfrac {dr}{dt_{r}}}\right)_{\text{raindrop}}}{\left({\dfrac {dr}{dt_{r}}}\right)_{\text{light}}}}={\frac {\sqrt {\dfrac {2M}{r}}}{1+{\sqrt {\dfrac {2M}{r}}}}}<1.$
2. Время прохождения света, падающего внутрь от горизонта событий до центра черной дыры, можно получить путем интегрирования уравнения для скорости света:

$\int _{0}^{T_{r}}\,dt=-\int _{2M}^{0}\left({\sqrt {\frac {2M}{r}}}+1\right)^{-1}\,dr.$

Результат $T_{r}=4M\ln 2-2M\approx 0.77M.$

1. Время прохождения света для звездной черной дыры с типичным размером в 3 солнечных массы составляет около 11 микросекунд.
2. Если не учитывать эффекты вращения, для Стрельца А* , сверхмассивной черной дыры , находящейся в центре Млечного Пути , с массой 3,7 миллиона солнечных масс, время прохождения света составляет около 14 секунд.
3. Сверхмассивная черная дыра в центре Мессье 87 , гигантской эллиптической галактики в скоплении Девы , является самой большой известной черной дырой. Его масса составляет около 3 миллиардов солнечных масс. Свету потребуется около 3 часов, чтобы добраться до центральной сингулярности такой сверхмассивной черной дыры, а дождевой капле — 5 часов.

Взгляд на Вселенную со стороны наблюдателя дождя

Как выглядит Вселенная, как ее видит наблюдатель за дождем, погружающийся в черную дыру? Представление можно описать следующими уравнениями:

$\cos {\boldsymbol {\Phi }}_{r}={\frac {dr_{r}}{dt_{r}}}={\frac {{\sqrt {\dfrac {2M}{r}}}+\cos {\boldsymbol {\Phi }}_{s}}{1+{\sqrt {\dfrac {2M}{r}}}\ \cos {\boldsymbol {\Phi }}_{s}}},\,$

$\cos {\boldsymbol {\Phi }}_{s}={\frac {dr_{s}}{dt_{s}}}=\pm {\sqrt {1-\left(1-{\frac {2M}{r}}\right){\frac {{\mathit {I}}^{2}}{r^{2}}}}},\,\!$

$\phi ={\mathit {I}}\int _{r_{0}}^{\infty }{\frac {dr}{r^{2}\ \cos {\boldsymbol {\Phi }}_{s}}},\,\!$

где

${\boldsymbol {\Phi }}_{r},\ {\boldsymbol {\Phi }}_{s}\,\!$ — углы обзора наблюдателя за дождем и наблюдателя за оболочкой по отношению к радиальному направлению наружу.

$\ \phi \,\!$ - это угол между далекой звездой и радиально внешним направлением.

${\mathit {I}}\,\!$ является ударным параметром. Каждый входящий луч света можно проследить до соответствующего луча на бесконечности. Параметр удара для падающего светового луча — это расстояние между соответствующим лучом на бесконечности и параллельным ему лучом, который падает прямо в черную дыру.

Из-за сферической симметрии траектория света всегда лежит в плоскости, проходящей через центр сферы. Можно упростить метрику, предположив $\theta ={\frac {\pi }{2}}\,\!$ .

Ударный параметр ${\mathit {I}}\,\!$ можно вычислить, зная r-координату наблюдателя за дождем $r_{0}\,\!$ и угол обзора $\ {\boldsymbol {\Phi }}_{r0}\,\!$ . Тогда реальный угол $\ \phi \,\!$ далекой звезды, определяется путем численного интегрирования $dr\,\!$ от $r_{0}\,\!$ до бесконечности. Диаграмма результатов выборки показана справа.

• При r / M = 500 черная дыра еще очень далеко. Он образует на небе диаметральный угол ~ 1 градус. Звезды не сильно искажаются присутствием черной дыры, за исключением звезд, находящихся непосредственно за ней. Из-за гравитационного линзирования эти закрытые звезды теперь отклонены на 5 градусов назад. Между этими звездами и черной дырой находится круглая полоса вторичных изображений звезд. Дублированные изображения помогают идентифицировать черную дыру.
• При r/M = 30 черная дыра стала намного больше, занимая на небе диаметральный угол ~15 градусов. Полоса вторичного изображения также выросла до 10 градусов. Теперь в полосе можно найти слабые третичные изображения, создаваемые световыми лучами, уже однажды обогнувшими черную дыру. Первичные изображения более плотно распределены на остальной части неба. Схема распределения аналогична той, что была показана ранее.
• При r/M = 2, горизонте событий, черная дыра теперь занимает значительную часть неба. Наблюдатель за дождем увидит область под углом до 42 градусов по радиальному направлению внутрь, где кромешная тьма. Полоса вторичного и третичного изображений не увеличилась, а уменьшилась в размерах до 5 градусов. Эффект аберрации теперь довольно доминирует. Скорость погружения достигла скорости света. Кардинально меняется характер распространения первичных изображений. Первичные изображения смещаются к границе полосы. Край возле полосы теперь заполнен звездами. Из-за эффекта Доплера первичное изображение звезд, которые изначально располагались за наблюдателем дождя, имеет заметное красное смещение, тогда как изображения тех, что были впереди, смещены в синее и кажутся очень яркими.
• При r/M=0,001 кривая зависимости угла обзора от далекой звезды от угла обзора образует прямой угол при угле обзора 90 градусов. Почти все изображения звезд собраны в узкое кольцо под углом 90 градусов к радиальному направлению. Между кольцом и радиально внутренним направлением находится огромная черная дыра. На противоположной стороне слабо светятся лишь несколько звезд.
• Когда наблюдатель дождя приближается к сингулярности, $r\rightarrow 0\,\!$, и $\cos {\boldsymbol {\Phi }}_{r}\rightarrow {\sqrt {\frac {r}{2M}}}\,\!$ . Большинство звезд и их изображения, вызванные множественными орбитами света вокруг черной дыры, сжимаются в узкую полосу под углом обзора 90°. Наблюдатель видит великолепное яркое кольцо звезд, делящее темное небо пополам.

История

Хотя публикация статьи Галлстранда последовала за статьей Пенлеве, статья Галлстранда была датирована 25 мая 1921 года, тогда как публикация Пенлеве представляла собой рецензию его выступления перед Академией наук в Париже 24 октября 1921 года. Таким образом, работа Галстранда, похоже, имеет приоритет.

И Пенлеве, и Галлстранд использовали это решение, чтобы доказать, что теория Эйнштейна была неполной, поскольку она давала несколько решений для гравитационного поля сферического тела и, более того, давала разную физику (они утверждали, что длина стержней иногда может быть длиннее, а иногда короче). радиальное, чем тангенциальное направления). «Хитрость» предложения Пенлеве заключалась в том, что он больше не придерживался полной квадратичной (статической) формы, а вместо этого допускал перекрестное произведение времени и пространства, делая метрическую форму больше не статичной, а стационарной и не симметричной по направлению, а предпочтительно ориентированной.

Во второй, более длинной статье (14 ноября 1921 г.) Пенлеве объясняет, как он получил свое решение путем прямого решения уравнений Эйнштейна для общей сферически-симметричной формы метрики. Результат, уравнение (4) его статьи, зависел от двух произвольных функций координаты r, что давало двойную бесконечность решений. Теперь мы знаем, что они просто представляют собой различные варианты выбора как времени, так и радиальных координат.

Пенлеве написал Эйнштейну, чтобы представить свое решение, и пригласил Эйнштейна в Париж для обсуждения. В ответном письме Эйнштейна (7 декабря): он извинился за то, что не сможет приехать в ближайшее время, и объяснил, почему его не устраивают аргументы Пенлеве, подчеркнув, что сами координаты не имеют значения. Наконец, Эйнштейн приехал в Париж в начале апреля. 5 апреля 1922 года на дебатах в Коллеж де Франс. вместе с Пенлеве, Беккерелем, Бриллюэном, Картаном, Де Дондером, Адамаром, Ланжевеном и Нордманом о «бесконечных потенциалах», Эйнштейн, сбитый с толку неквадратичным перекрестным членом в линейном элементе, отверг решение Пенлеве.

См. также

• Изотропные координаты
• Координаты Эддингтона – Финкельштейна
• Координаты Крускала – Секереса
• Подробности о Леметре

Ссылки

• Миснер, Торн, Уиллер (1973). Гравитация . WH Фриман и компания. ISBN  0-7167-0344-0 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )

Внешние ссылки

• Речная модель черных дыр
• Видео доктора Эндрю Дж. С. Гамильтона «Внутри черных дыр»
• Моделирование орбиты черной дыры в координатах GP.