Скорость

Скорость
Скорость
	Поскольку изменение направления происходит во время поворота гоночных автомобилей на изогнутой трассе, их скорость не является постоянной, даже если их скорость постоянна.
Общие символы	v , v , v → , v
Другие подразделения	миль в час , фут/с
В базовых единицах СИ	РС
Измерение	Л Т −1

Скорость — это в сочетании с направлением движения объекта . скорость Скорость — фундаментальное понятие кинематики , раздела классической механики , описывающего движение тел.

Скорость — это физическая векторная величина : для ее определения необходимы как величина, так и направление. Скалярное . абсолютное значение ( величина ) скорости называется скоростью и представляет собой последовательную производную единицу, величина которой измеряется в СИ ( метрической системе ) в метрах в секунду (м/с или м⋅с) ⁻¹). Например, «5 метров в секунду» — это скаляр, тогда как «5 метров в секунду на восток» — это вектор. Если происходит изменение скорости, направления или того и другого, то говорят, что объект испытывает ускорение .

Определение

Средняя скорость

Средняя скорость объекта за период времени – это изменение его положения , $\Delta s$ , разделенный на продолжительность периода, $\Delta t$ , заданный математически как ^[1]

{\bar {v}}={\frac {\Delta s}{\Delta t}}.

Мгновенная скорость

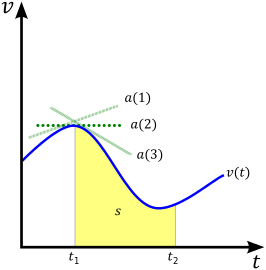
Мгновенная . скорость объекта — это предельная средняя скорость на промежутке времени, приближающемся к нулю В любой конкретный момент времени $t$ его можно рассчитать как производную положения по времени: ^[2]

{\boldsymbol {v}}=\lim _{{\Delta t}\to 0}{\frac {\Delta {\boldsymbol {s}}}{\Delta t}}={\frac {d{\boldsymbol {s}}}{dt}}.

Из этого производного уравнения в одномерном случае видно, что площадь под зависимостью скорости от времени ( $график v$ от $t$ ) представляет собой смещение, $s$ . В терминах исчисления интеграл функции скорости $v (t)$ представляет собой функцию смещения $s (t)$ . На рисунке это соответствует желтой области под кривой.

{\boldsymbol {s}}=\int {\boldsymbol {v}}\ dt.

Хотя концепция мгновенной скорости может на первый взгляд показаться нелогичной, ее можно рассматривать как скорость, с которой объект продолжал бы двигаться, если бы в этот момент он прекратил ускоряться.

Разница между скоростью и скоростью

Кинематические величины классической частицы: масса m , положение r , скорость v , ускорение a .

Хотя термины «скорость» и «скорость» в разговорной речи часто используются как синонимы, обозначая, насколько быстро движется объект, с научной точки зрения они разные. Скорость, скалярная величина вектора скорости, обозначает только то, насколько быстро движется объект, тогда как скорость указывает как скорость, так и направление объекта. ^[3]^[4]^[5]

Чтобы иметь постоянную скорость , объект должен иметь постоянную скорость в постоянном направлении. Постоянное направление вынуждает объект двигаться по прямой траектории, поэтому постоянная скорость означает движение по прямой линии с постоянной скоростью.

Например, автомобиль, движущийся по круговой траектории с постоянной скоростью 20 километров в час, имеет постоянную скорость, но не имеет постоянной скорости, поскольку его направление меняется. Следовательно, считается, что автомобиль испытывает ускорение.

Единицы

Поскольку производная положения по времени дает изменение положения (в метрах ), деленное на изменение во времени (в секундах ), скорость измеряется в метрах в секунду (м/с).

Уравнение движения

Средняя скорость

Скорость определяется как скорость изменения положения во времени, которую также можно называть мгновенной скоростью, чтобы подчеркнуть отличие от средней скорости. В некоторых приложениях может потребоваться средняя скорость объекта, то есть постоянная скорость, которая обеспечит то же результирующее смещение, что и переменная скорость, в том же интервале времени $v (t)$ в течение некоторого периода времени $Δ t$ . Среднюю скорость можно рассчитать как: ^[6]^[7]

\mathbf {\bar {v}} ={\frac {\Delta \mathbf {x} }{\Delta t}}={\frac {\int _{t_{0}}^{t_{1}}\mathbf {v} (t)dt}{t_{1}-t_{0}}}.

Средняя скорость всегда меньше или равна средней скорости объекта. В этом можно убедиться, осознав, что хотя расстояние всегда строго увеличивается, смещение может увеличиваться или уменьшаться по величине, а также изменять направление.

На графике зависимости времени перемещения ( $x$ от $t$ ) мгновенную скорость (или просто скорость) можно рассматривать как наклон касательной к кривой в любой точке , а среднюю скорость — как наклон секущей линии между двумя точками с $координатами t$ , равными границам периода времени для средней скорости.

Особые случаи

Когда частица движется с разными равномерными скоростями v ₁ , v ₂ , v ₃ , ..., v _n в разные промежутки времени t ₁ , t ₂ , t ₃ , ..., t _n соответственно, то средняя скорость по всей сумме время в пути указано как ${\bar {v}}={v_{1}t_{1}+v_{2}t_{2}+v_{3}t_{3}+\dots +v_{n}t_{n} \over t_{1}+t_{2}+t_{3}+\dots +t_{n}}$

Если $t 1 = t 2 = t 3 = ... = t$ , то средняя скорость определяется как среднее арифметическое скоростей

{\bar {v}}={v_{1}+v_{2}+v_{3}+\dots +v_{n} \over n}={\frac {1}{n}}\sum _{i=1}^{n}{v_{i}}

Когда частица перемещается на разные расстояния со _{скоростями} v 1 _, v 2 _, v 3 _{s 1 , s 2 , s 3 ,..., sn} , ... _, v n _{соответственно} , то _{средняя} скорость частицы _за всю расстояние дано как ^[8]

{\bar {v}}={s_{1}+s_{2}+s_{3}+\dots +s_{n} \over t_{1}+t_{2}+t_{3}+\dots +t_{n}}={{s_{1}+s_{2}+s_{3}+\dots +s_{n}} \over {{s_{1} \over v_{1}}+{s_{2} \over v_{2}}+{s_{3} \over v_{3}}+\dots +{s_{n} \over v_{n}}}}

Если

s 1 = s 2 = s 3 = ... = s

, то средняя скорость определяется средним гармоническим значением скоростей. ^[8]

{\bar {v}}=n\left({1 \over v_{1}}+{1 \over v_{2}}+{1 \over v_{3}}+\dots +{1 \over v_{n}}\right)^{-1}=n\left(\sum _{i=1}^{n}{\frac {1}{v_{i}}}\right)^{-1}.

Связь с ускорением

объекта Хотя скорость определяется как скорость изменения положения, часто принято начинать с выражения для ускорения . Как видно по трем зеленым касательным линиям на рисунке, мгновенное ускорение объекта в определенный момент времени представляет собой наклон линии, касательной к кривой $графика v (t)$ в этой точке. Другими словами, мгновенное ускорение определяется как производная скорости по времени: ^[9]

{\boldsymbol {a}}={\frac {d{\boldsymbol {v}}}{dt}}.

Отсюда мы можем получить выражение для скорости как площадь под $графиком зависимости ускорения a (t)$ от времени. Как и выше, это делается с помощью понятия интеграла:

{\boldsymbol {v}}=\int {\boldsymbol {a}}\ dt.

Постоянное ускорение

В частном случае постоянного ускорения скорость можно изучить с помощью уравнений Сувата . Рассматривая a как равное некоторому произвольному постоянному вектору, легко показать, что

{\boldsymbol {v}}={\boldsymbol {u}}+{\boldsymbol {a}}t

где

v

— скорость в момент времени

t

, а

u

— скорость в момент времени

t = 0

. Объединив это уравнение с уравнением Сувата

x = u t + a t 2 /2

можно связать перемещение и среднюю скорость соотношением

{\boldsymbol {x}}={\frac {({\boldsymbol {u}}+{\boldsymbol {v}})}{2}}t={\boldsymbol {\bar {v}}}t.

Также возможно вывести выражение для скорости, не зависящее от времени, известное как уравнение Торричелли , следующим образом:

v^{2}={\boldsymbol {v}}\cdot {\boldsymbol {v}}=({\boldsymbol {u}}+{\boldsymbol {a}}t)\cdot ({\boldsymbol {u}}+{\boldsymbol {a}}t)=u^{2}+2t({\boldsymbol {a}}\cdot {\boldsymbol {u}})+a^{2}t^{2}

(2{\boldsymbol {a}})\cdot {\boldsymbol {x}}=(2{\boldsymbol {a}})\cdot ({\boldsymbol {u}}t+{\tfrac {1}{2}}{\boldsymbol {a}}t^{2})=2t({\boldsymbol {a}}\cdot {\boldsymbol {u}})+a^{2}t^{2}=v^{2}-u^{2}

\therefore v^{2}=u^{2}+2({\boldsymbol {a}}\cdot {\boldsymbol {x}})

где

v = | в |

и т. д.

Приведенные выше уравнения справедливы как для механики Ньютона, так и для специальной теории относительности . Механика Ньютона и специальная теория относительности различаются тем, как разные наблюдатели описывают одну и ту же ситуацию. В частности, в механике Ньютона все наблюдатели соглашаются со значением t, а правила преобразования положения создают ситуацию, в которой все неускоряющиеся наблюдатели описывали бы ускорение объекта с одинаковыми значениями. Ни то, ни другое не верно для специальной теории относительности. Другими словами, можно рассчитать только относительную скорость.

Величины, зависящие от скорости

Импульс

В классической механике второй закон Ньютона определяет импульс p как вектор, который является произведением массы и скорости объекта, математически определяемого как

{\boldsymbol {p}}=m{\boldsymbol {v}}

где m — масса объекта.

Кинетическая энергия

Кинетическая энергия движущегося объекта зависит от его скорости и определяется уравнением ^[10]

E_{\text{k}}={\tfrac {1}{2}}mv^{2}

где E _k – кинетическая энергия. Кинетическая энергия является скалярной величиной, поскольку зависит от квадрата скорости.

Перетаскивание (сопротивление жидкости)

В гидродинамике сопротивление — это сила , действующая противоположно относительному движению любого объекта, движущегося относительно окружающей жидкости. Сила сопротивления, $F_{D}$ , зависит от квадрата скорости и определяется как

F_{D}\,=\,{\tfrac {1}{2}}\,\rho \,v^{2}\,C_{D}\,A

где

$\rho$ - плотность жидкости, ^[11]
$v$ - скорость объекта относительно жидкости,
$A$ - площадь поперечного сечения , а
$C_{D}$ – коэффициент аэродинамического сопротивления – безразмерное число .

Скорость убегания

Скорость убегания — это минимальная скорость, необходимая баллистическому объекту для отрыва от массивного тела, такого как Земля. объекта Она представляет собой кинетическую энергию, которая при добавлении к гравитационной потенциальной энергии (которая всегда отрицательна) равна нулю. Общая формула скорости убегания объекта на расстоянии r от центра планеты с массой M : ^[12]

v_{\text{e}}={\sqrt {\frac {2GM}{r}}}={\sqrt {2gr}},

где G — гравитационная постоянная , а g — гравитационное ускорение . Скорость отрыва от поверхности Земли составляет около 11 200 м/с и не зависит от направления объекта. Это делает термин «скорость убегания» в некоторой степени неправильным, поскольку более правильным термином было бы «скорость убегания»: любой объект, достигающий скорости этой величины, независимо от атмосферы, покинет окрестности основного тела до тех пор, пока он не пересекаться с чем-либо на своем пути.

Фактор Лоренца специальной теории относительности

В специальной теории относительности часто появляется безразмерный фактор Лоренца и определяется выражением ^[13]

\gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}

где γ — фактор Лоренца, а c — скорость света.

Относительная скорость

Относительная скорость — это измерение скорости между двумя объектами, определенной в одной системе координат. Относительная скорость имеет фундаментальное значение как в классической, так и в современной физике, поскольку многие физические системы имеют дело с относительным движением двух или более частиц.

Рассмотрим объект A, движущийся с вектором скорости v, и объект B с вектором скорости w ; эти абсолютные скорости обычно выражаются в одной и той же инерциальной системе отсчета . Тогда скорость объекта A относительно объекта B определяется как разность двух векторов скорости:

{\boldsymbol {v}}_{A{\text{ relative to }}B}={\boldsymbol {v}}-{\boldsymbol {w}}

Аналогично, относительная скорость объекта B, движущегося со скоростью w , относительно объекта A, движущегося со скоростью v , равна:

{\boldsymbol {v}}_{B{\text{ relative to }}A}={\boldsymbol {w}}-{\boldsymbol {v}}

Обычно в качестве инерциальной системы отсчета выбирают ту, в которой покоится последний из двух упомянутых объектов.

В механике Ньютона относительная скорость не зависит от выбранной инерциальной системы отсчета. Это уже не относится к специальной теории относительности , в которой скорости зависят от выбора системы отсчета.

Скалярные скорости

В одномерном случае ^[14] скорости являются скалярами, и уравнение имеет вид:

v_{\text{rel}}=v-(-w),

если два объекта движутся в противоположных направлениях, или:

v_{\text{rel}}=v-(+w),

если два объекта движутся в одном направлении.

Системы координат

Декартовы координаты

В многомерных декартовых системах координат скорость разбивается на компоненты, соответствующие каждой размерной оси системы координат. В двумерной системе, где есть оси x и y, соответствующие компоненты скорости определяются как ^[15]

v_{x}=dx/dt,

v_{y}=dy/dt.

Тогда двумерный вектор скорости определяется как ${\textbf {v}}=<v_{x},v_{y}>$ . Величина этого вектора представляет скорость и находится по формуле расстояния как

|v|={\sqrt {v_{x}^{2}+v_{y}^{2}}}.

В трехмерных системах, где имеется дополнительная ось z, соответствующая компонента скорости определяется как

v_{z}=dz/dt.

Трехмерный вектор скорости определяется как ${\textbf {v}}=<v_{x},v_{y},v_{z}>$ причем его величина также представляет скорость и определяется

|v|={\sqrt {v_{x}^{2}+v_{y}^{2}+v_{z}^{2}}}.

В то время как в некоторых учебниках для определения декартовых компонентов скорости используется индексная запись, в других используются $u$ , $v$ , и $w$ для $x$ -, $y$ -, и $z$ -оси соответственно. ^[16]

Полярные координаты

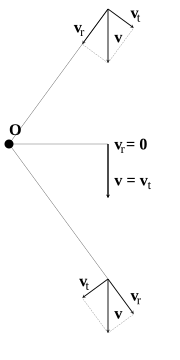
В полярных координатах двумерная скорость описывается радиальной скоростью , определяемой как составляющая скорости от начала координат или к началу координат, и поперечной скоростью , перпендикулярной радиальной. ^[17]^[18] Оба возникают из-за угловой скорости , которая представляет собой скорость вращения вокруг начала координат (положительные величины представляют вращение против часовой стрелки, а отрицательные величины представляют вращение по часовой стрелке в правосторонней системе координат).

Радиальная и поперечная скорости могут быть получены из декартовых векторов скорости и смещения путем разложения вектора скорости на радиальную и поперечную составляющие. Поперечная . скорость — это составляющая скорости вдоль окружности с центром в начале координат

{\boldsymbol {v}}={\boldsymbol {v}}_{T}+{\boldsymbol {v}}_{R}

где

${\boldsymbol {v}}_{T}$ поперечная скорость
${\boldsymbol {v}}_{R}$ – лучевая скорость.

Радиальная скорость (или величина радиальной скорости) представляет собой скалярное произведение вектора скорости и единичного вектора в радиальном направлении.

v_{R}={\frac {{\boldsymbol {v}}\cdot {\boldsymbol {r}}}{\left|{\boldsymbol {r}}\right|}}={\boldsymbol {v}}\cdot {\hat {\boldsymbol {r}}}

где

{\boldsymbol {r}}

это позиция и

{\hat {\boldsymbol {r}}}

является радиальным направлением.

Поперечная скорость (или величина поперечной скорости) представляет собой величину векторного произведения единичного вектора в радиальном направлении и вектора скорости. Это также скалярное произведение скорости и поперечного направления или произведение угловой скорости . $\omega$ и радиус (величина положения).

v_{T}={\frac {|{\boldsymbol {r}}\times {\boldsymbol {v}}|}{|{\boldsymbol {r}}|}}={\boldsymbol {v}}\cdot {\hat {\boldsymbol {t}}}=\omega |{\boldsymbol {r}}|

такой, что

\omega ={\frac {|{\boldsymbol {r}}\times {\boldsymbol {v}}|}{|{\boldsymbol {r}}|^{2}}}.

Угловой момент в скалярной форме равен массе, умноженной на расстояние до начала координат, умноженной на поперечную скорость, или, что эквивалентно, массе, умноженной на квадрат расстояния, умноженной на угловую скорость. Соглашение о знаках для углового момента такое же, как и для угловой скорости.

L=mrv_{T}=mr^{2}\omega

где

$m$ масса
$r=|{\boldsymbol {r}}|.$

Выражение $mr^{2}$ известен как момент инерции . Если силы действуют в радиальном направлении только с обратной квадратичной зависимостью, как в случае гравитационной орбиты , угловой момент постоянен, а поперечная скорость обратно пропорциональна расстоянию, угловая скорость обратно пропорциональна квадрату расстояния, а Скорость выметания территории постоянна. Эти соотношения известны как законы движения планет Кеплера .

Смотрите также

Четырехскоростная (релятивистская версия скорости для пространства-времени Минковского )
Групповая скорость
Гиперскорость
Фазовая скорость
Правильная скорость (в теории относительности используется время путешественника вместо времени наблюдателя)
Быстрота (вариант добавки скорости на релятивистских скоростях)
Предельная скорость
Поле скорости
График зависимости скорости от времени

Примечания

Роберт Резник и Джерл Уокер, «Основы физики» , Wiley; 7 Подвыпуск (16 июня 2004 г.). ISBN 0-471-23231-9 .

Внешние ссылки

[1] «Фейнмановские лекции по физике, том I, глава 8: Движение» . www.feynmanlectures.caltech.edu . Проверено 5 января 2024 г.

[2] Дэвид Холлидей; Роберт Резник; Джерл Уокер (2021). Основы физики, расширенное (12-е изд.). Джон Уайли и сыновья. п. 71. ИСБН 978-1-119-77351-1 . Выдержка со страницы 71

[3] Ричард П. Оленик; Том М. Апостол; Дэвид Л. Гудштейн (2008). Механическая Вселенная: Введение в механику и тепло (иллюстрировано, переиздано под ред.). Издательство Кембриджского университета. п. 84. ИСБН 978-0-521-71592-8 . Выдержка со страницы 84

[4] Майкл Дж. Кардамон (2007). Фундаментальные понятия физики . Универсал-Издательство. п. 5. ISBN 978-1-59942-433-0 . Выдержка из страницы 5

[5] Джерри Д. Уилсон; Энтони Дж. Буффа; Бо Лу (2022). Основы физики для колледжа, восьмое издание (двухтомный набор) (иллюстрированное издание). ЦРК Пресс. п. 40. ИСБН 978-1-351-12991-6 . Выдержка со страницы 40

[6] Дэвид Холлидей; Роберт Резник; Джерл Уокер (2021). Основы физики, расширенное (12-е изд.). Джон Уайли и сыновья. п. 70. ИСБН 978-1-119-77351-1 . Выдержка со страницы 70

[7] Адриан Баннер (2007). Спасатель исчисления: все инструменты, необходимые для достижения успеха в исчислении (иллюстрированное издание). Издательство Принстонского университета. п. 350. ИСБН 978-0-691-13088-0 . Выдержка со страницы 350

[giba-8] Перейти обратно: ^а ^б Гири и Баннерджи (2002). Статистические инструменты и методы . Академические издательства. п. 4. ISBN 978-81-87504-39-9 . Выдержка со страницы 4

[9] Бекир Караоглу (2020). Классическая физика: Учебник для двух семестров . Спрингер Природа. п. 41. ИСБН 978-3-030-38456-2 . Выдержка со страницы 41

[10] Дэвид Холлидей; Роберт Резник; Джерл Уокер (2010). Основы физики, главы 33-37 . Джон Уайли и сыновья. п. 1080. ИСБН 978-0-470-54794-6 . Выдержка из страницы 1080

[11] Для атмосферы Земли плотность воздуха можно найти по барометрической формуле . Это 1,293 кг/м. ³ при 0°С и 1 атмосфере .

[12] Джим Брейтаупт (2000). Новое понимание физики для продвинутого уровня (иллюстрированное издание). Нельсон Торнс. п. 231. ИСБН 978-0-7487-4314-8 . Выдержка со страницы 231

[13] Эккехард В. Мильке (2022). Современные аспекты теории относительности . Всемирная научная. п. 98. ИСБН 978-981-12-4406-3 . Выдержка со страницы 98

[14] Основной принцип

[15] «Лекции Фейнмана по физике, том I, глава 9: Законы динамики Ньютона» . www.feynmanlectures.caltech.edu . Проверено 4 января 2024 г.

[16] Уайт, FM (2008). Механика жидкости . Компании МакГроу Хилл.

[17] Э. Грэм; Эйдан Берроуз; Брайан Голтер (2002). Механика, Том 6 (иллюстрированное изд.). Хайнеманн. п. 77. ИСБН 978-0-435-51311-5 . Выдержка со страницы 77

[18] Ануп Гоэль; Х. Дж. Савант (2021). Инженерная механика . Технические публикации. п. 8. ISBN 978-93-332-2190-0 . Выдержка со страницы 8

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

Определение

Средняя скорость

Мгновенная скорость

Разница между скоростью и скоростью

Единицы

Уравнение движения

Средняя скорость

Особые случаи

Связь с ускорением

Постоянное ускорение

Величины, зависящие от скорости

Импульс

Кинетическая энергия

Перетаскивание (сопротивление жидкости)

Скорость убегания

Фактор Лоренца специальной теории относительности

Относительная скорость

Скалярные скорости

Системы координат

Декартовы координаты

Полярные координаты

Смотрите также

Примечания

Рекомендации

Внешние ссылки