Система отсчета
| Часть серии о |
| Классическая механика |
|---|
В физике и астрономии система отсчета (или система отсчета ) — это абстрактная система координат которой начало координат , , ориентация и масштаб задаются набором опорных точек — геометрических точек которых , положение определяется как математически (с помощью числовых значений координат), так и физически (обозначается обычными маркерами). [1]
Для n измерений n + 1 опорных точек достаточно, чтобы полностью определить систему отсчета. Используя прямоугольные декартовы координаты , система отсчета может быть определена с опорной точкой в начале координат и опорной точкой на расстоянии одной единицы вдоль каждой из n координатных осей . [ нужна ссылка ]
В теории относительности Эйнштейна системы отсчета используются для определения связи между движущимся наблюдателем и наблюдаемым явлением. В этом контексте термин часто становится системой отсчета наблюдения (или системой отсчета наблюдения ), что подразумевает, что наблюдатель покоится в системе отсчета, хотя и не обязательно находится в ее начале . Релятивистская система отсчета включает (или подразумевает) координатное время , которое не уравнивает различные системы отсчета, движущиеся относительно друг друга. Таким образом, ситуация отличается от теории относительности Галилея , в которой все возможные координатные времена по существу эквивалентны. [ нужна ссылка ]
Определение [ править ]
Необходимость различать различные значения «системы отсчета» привела к появлению множества терминов. Например, иногда тип системы координат присоединяется как модификатор, как в декартовой системе отсчета . Иногда подчеркивается состояние движения, как, например, во вращающейся системе отсчета . Иногда подчеркивается, как он преобразуется в системы отсчета, считающиеся связанными, как в системе отсчета Галилея . Иногда системы отсчета различаются по масштабу наблюдений, как в макроскопических и микроскопических системах отсчета . [2]
В этой статье термин « система отсчета наблюдения» используется, когда акцент делается на состоянии движения, а не на выборе координат или характере наблюдений или наблюдательного аппарата. В этом смысле наблюдательная система отсчета позволяет изучать влияние движения на целое семейство систем координат, которые могут быть привязаны к этой системе отсчета. С другой стороны, система координат может использоваться для многих целей, где состояние движения не является основной проблемой. Например, может быть принята система координат, позволяющая воспользоваться преимуществами симметрии системы. В еще более широкой перспективе при формулировке многих задач физики используются обобщенные координаты , нормальные моды или собственные векторы , которые лишь косвенно связаны с пространством и временем. Представляется полезным разделить различные аспекты системы отсчета для обсуждения ниже. Поэтому мы принимаем системы отсчета наблюдения, системы координат и оборудование для наблюдений как независимые понятия, разделенные следующим образом:
- Система наблюдения (например, инерциальная система отсчета или неинерциальная система отсчета ) — это физическое понятие, связанное с состоянием движения.
- Система координат — это математическое понятие, определяющее выбор языка, используемого для описания наблюдений. [3] Следовательно, наблюдатель в системе отсчета наблюдения может использовать любую систему координат (декартову, полярную, криволинейную, обобщенную и т. д.) для описания наблюдений, сделанных из этой системы отсчета. Изменение выбора этой системы координат не меняет состояния движения наблюдателя и, следовательно, не влечет за собой изменения системы отсчета наблюдателя . Эту точку зрения можно найти и в других местах. [4] Нельзя оспаривать тот факт, что некоторые системы координат могут быть лучшим выбором для одних наблюдений, чем другие.
- Выбор того, что измерять и с помощью какой наблюдательной аппаратуры, — дело отдельное от состояния движения наблюдателя и выбора системы координат.
Системы координат [ править ]
Хотя термин «система координат» часто используется (особенно физиками) в нетехническом смысле, термин «система координат» имеет точное значение в математике, а иногда именно это имеют в виду и физики.
Система координат в математике — это аспект геометрии или алгебры . [9] [10] в частности, свойство многообразий ( например, в физике, конфигурационных пространствах или фазовых пространствах ). [11] [12] Координаты -мерном пространстве представляют собой точки r в n просто упорядоченный набор из n чисел: [13] [14]
В общем банаховом пространстве эти числа могут быть (например) коэффициентами функционального разложения, такого как ряд Фурье . В физической задаче это могут быть координаты пространства-времени или амплитуды нормальной моды . В конструкции робота это могут быть углы относительных поворотов, линейные перемещения или деформации суставов . [15] Здесь мы предположим, что эти координаты могут быть связаны с декартовой системой координат набором функций:
где x , y , z и т . д. — n декартовых координат точки. Учитывая эти функции, координатные поверхности определяются соотношениями:
Пересечение этих поверхностей определяют координатные линии . В любой выбранной точке касательные к пересекающимся координатным линиям в этой точке определяют набор базисных векторов { e 1 , e 2 , ..., } en в этой точке. То есть: [16]
который можно нормализовать до единичной длины. Подробнее см. криволинейные координаты .
Координатные поверхности, координатные линии и базисные векторы являются компонентами системы координат . [17] Если базисные векторы ортогональны в каждой точке, система координат является ортогональной системой координат .
Важным аспектом системы координат является ее метрический тензор g ik , определяющий длину дуги ds в системе координат через ее координаты: [18]
где повторяющиеся индексы суммируются.
Как видно из этих замечаний, система координат — это математическая конструкция , часть аксиоматической системы . Между системами координат и физическим движением (или любым другим аспектом реальности) нет необходимой связи. Однако системы координат могут включать время в качестве координаты и использоваться для описания движения. Таким образом, преобразования Лоренца и преобразования Галилея можно рассматривать как преобразования координат .
Система наблюдений [ править ]

Система отсчета наблюдения , часто называемая физической системой отсчета , системой отсчета или просто рамкой , представляет собой физическую концепцию, связанную с наблюдателем и состоянием движения наблюдателя. Здесь мы принимаем точку зрения, высказанную Кумаром и Барве: система отсчета наблюдения характеризуется только состоянием ее движения . [19] Однако единогласия по этому вопросу нет. В специальной теории относительности иногда проводится различие между наблюдателем и системой отсчета . Согласно этой точке зрения, рамка представляет собой наблюдателя плюс координатную решетку, построенную как ортонормированный правый набор пространственноподобных векторов, перпендикулярных времениподобному вектору. См. Дорана. [20] Эта ограниченная точка зрения здесь не используется и не принимается повсеместно даже при обсуждении теории относительности. [21] [22] В общей теории относительности распространено использование общих систем координат (см., например, решение Шварцшильда для гравитационного поля вне изолированной сферы [23] ).
Существует два типа систем отсчета наблюдения: инерциальная и неинерциальная . Инерциальная система отсчета определяется как система, в которой все законы физики принимают простейшую форму. В специальной теории относительности эти системы связаны преобразованиями Лоренца , которые параметризуются быстротой . В ньютоновской механике более ограниченное определение требует только первого закона Ньютона соблюдения ; то есть ньютоновская инерциальная система отсчета — это система, в которой свободная частица движется по прямой с постоянной скоростью или находится в состоянии покоя. Эти рамки связаны преобразованиями Галилея . Эти релятивистские и ньютоновские преобразования выражаются в пространствах общей размерности через представления группы Пуанкаре и группы Галилея .
В отличие от инерциальной системы отсчета, неинерциальная система отсчета — это система, в которой фиктивные силы для объяснения наблюдений необходимо использовать . Примером может служить система отсчета наблюдения с центром в точке на поверхности Земли. Эта система отсчета вращается вокруг центра Земли, что вводит фиктивные силы, известные как сила Кориолиса , центробежная сила и гравитационная сила . (Все эти силы, включая гравитацию, исчезают в истинно инерциальной системе отсчета, которая представляет собой систему свободного падения.)
Измерительная аппаратура [ править ]
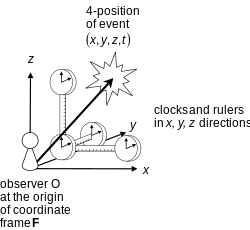
Еще одним аспектом системы отсчета является роль измерительного прибора (например, часов и стержней), прикрепленного к системе (см. цитату Нортона выше). Этот вопрос не рассматривается в этой статье и представляет особый интерес для квантовой механики , где связь между наблюдателем и измерением все еще обсуждается (см. Проблема измерения ).
В физических экспериментах систему отсчета, в которой покоятся лабораторные измерительные приборы, обычно называют лабораторной системой отсчета или просто «лабораторной системой отсчета». Примером может служить кадр, в котором детекторы ускорителя частиц покоятся. Лабораторная система координат в некоторых экспериментах является инерциальной системой отсчета, но это не обязательно (например, лаборатория на поверхности Земли во многих физических экспериментах не является инерциальной). В экспериментах по физике элементарных частиц часто бывает полезно преобразовать энергии и импульсы частиц из лабораторной системы координат, где они измеряются, в центр системы импульсов «кадр COM», в котором расчеты иногда упрощаются, поскольку потенциально вся кинетическая энергия все еще присутствует в кадр COM может использоваться для создания новых частиц.
В этой связи можно отметить, что часы и стержни, часто используемые в мыслях для описания измерительного оборудования наблюдателей, на практике заменяются гораздо более сложной и косвенной метрологией , связанной с природой вакуума и использующей атомные часы , которые работают в соответствии со стандартной моделью , и это необходимо скорректировать с учетом гравитационного замедления времени . [24] (См. секунда , метр и килограмм ).
Фактически Эйнштейн считал, что часы и стержни — это всего лишь удобные измерительные приборы, и их следует заменить более фундаментальными объектами, основанными, например, на атомах и молекулах. [25]
Обобщение [ править ]
Обсуждение выходит за рамки простых систем координат пространства-времени Брэйдинга и Кастеллани. [26] Расширение систем координат с использованием обобщенных координат лежит в основе гамильтоновой и лагранжевой формулировок. [27] квантовой теории поля , классической релятивистской механики и квантовой гравитации . [28] [29] [30] [31] [32]
Экземпляры [ править ]
- Международная наземная система отсчета
- Международная небесная система отсчета
- В механике жидкости лагранжева и эйлерова спецификация поля потока.
- Другие кадры
См. также [ править ]
- Аналитическая механика
- Прикладная механика
- Декартова система координат
- Рамка центра импульса
- Центробежная сила
- Центростремительная сила
- Классическая механика
- сила Кориолиса
- Криволинейные координаты
- Ссылка на датум
- Динамика (физика)
- Формулы Френе – Серре
- Галилеева инвариантность
- Общая теория относительности
- Обобщенные координаты
- Обобщенные силы
- Геодезическая система отсчета
- Инерциальная система отсчета
- Местные координаты
- Материальный каркас-безразличие
- Испытание стержня и рамы
- Кинематика
- Лабораторная система координат
- Преобразование Лоренца
- Принцип Маха
- Ортогональные координаты
- Принцип относительности
- Квантовая система отсчета
Примечания [ править ]
- ^ Вот цитата, применимая к движущимся системам наблюдения. и различные связанные с ними евклидовы трехпространственные системы координат [ R , R ' и т. д. ]: [5]
Сначала мы введем понятие системы отсчета , которое само по себе связано с идеей наблюдателя : система отсчета — это в некотором смысле «евклидово пространство, переносимое наблюдателем». Дадим более математическое определение:… система отсчета – это… совокупность всех точек евклидова пространства при твердотельном движении наблюдателя. Рамка, обозначенная Говорят, что , движется вместе с наблюдателем.… Пространственные положения частиц помечены относительно рамки установив координат R с началом координат O. систему Соответствующий набор осей, разделяющий движение твердого тела рамы. , можно считать дающим физическую реализацию . В рамке , координаты изменяются с R на R' путем выполнения в каждый момент времени одного и того же преобразования координат компонентов внутренних объектов (векторов и тензоров), введенных для представления физических величин в этой системе отсчета .
и это касается полезности разделения понятий и [ R , R′ и т. д. ]: [6]
Как отмечал Бриллюэн, необходимо проводить различие между математическими наборами координат и физическими системами отсчета. Незнание такого различия является источником большой путаницы… зависимые функции, такие как скорость, например, измеряются относительно физической системы отсчета, но каждый волен выбирать любую математическую систему координат, в которой заданы уравнения.
и это также касается различия между и [ R , R′ и т. д. ]: [7]
Идея системы отсчета на самом деле сильно отличается от идеи системы координат. Фреймы различаются только тогда, когда они определяют разные пространства (наборы точек отдыха ) или времена (наборы одновременных событий). Таким образом, идеи пространства, времени, покоя и одновременности неразрывно связаны с идеями кадра. Однако простой сдвиг начала координат или чисто пространственный поворот пространственных координат приводит к появлению новой системы координат. Таким образом, кадры в лучшем случае соответствуют классам систем координат.
и от Джей Ди Нортона: [8]
В традиционных разработках специальной и общей теории относительности было принято не различать две совершенно разные идеи. Первое — это понятие системы координат, понимаемое просто как плавное, обратимое присвоение четырех чисел событиям в окрестностях пространства-времени. Вторая, система отсчета, относится к идеализированной системе, используемой для присвоения таких чисел […] Чтобы избежать ненужных ограничений, мы можем отделить эту систему от метрических понятий. […] Для наших целей особое значение имеет то, что каждая система отсчета имеет определенное состояние движения в каждом событии пространства-времени. […] В контексте специальной теории относительности и до тех пор, пока мы ограничиваемся системами отсчета в инерциальном движении, малое значение имеет разница между инерциальной системой отсчета и инерциальной системой координат, которую она порождает. Это удобное обстоятельство немедленно исчезает, как только мы начинаем рассматривать системы отсчета в неравномерном движении даже в рамках специальной теории относительности.… Совсем недавно, чтобы преодолеть очевидную двусмысленность трактовки Эйнштейна, понятие системы отсчета вновь появилось как структура, отличная от системы координат. .
Ссылки [ править ]
- ^ Ковалевский Ю. ; Мюллер, Иван И. (1989). "Введение". Эталонные кадры . Библиотека астрофизики и космических наук. Том. 154. Дордрехт: Springer Нидерланды. стр. 1–12. дои : 10.1007/978-94-009-0933-5_1 . ISBN 978-94-010-6909-0 . ISSN 0067-0057 .
- ^ Различие между макроскопическими и микроскопическими системами отсчета проявляется, например, в электромагнетизме, где определяющие соотношения различных масштабов времени и длины используются для определения плотности тока и заряда, входящих в уравнения Максвелла . См., например, Курт Эдмунд Огстун (2006). Распространение электромагнитных и оптических импульсов 1: Спектральные представления в средах с дисперсией во времени . Спрингер. п. 165. ИСБН 0-387-34599-Х . . Эти различия проявляются и в термодинамике. Видеть Пол МакЭвой (2002). Классическая теория . МикроАналитикс. п. 205. ИСБН 1-930832-02-8 . .
- ^ В самых общих чертах система координат — это набор дуг x я = х я ( t ) в комплексной группе Ли ; видеть Лев Семенович Понтрягин (1986). Л. С. Понтрягин: Избранные сочинения. 2: Топологические группы (3-е изд.). Гордон и Брич. п. 429. ИСБН 2-88124-133-6 . . Менее абстрактно, система координат в пространстве n-мерностей определяется в терминах базисного набора векторов { e 1 , e 2 ,... e n }; видеть Эдоардо Сернеси; Дж. Монтальди (1993). Линейная алгебра: геометрический подход . ЦРК Пресс. п. 95. ИСБН 0-412-40680-2 . По сути, система координат представляет собой математическую конструкцию, язык, который может быть связан с движением, но не имеет необходимой связи с движением.
- ^ JX Чжэн-Йоханссон; Пер-Ивар Йоханссон (2006). Объединение классической, квантовой и релятивистской механики и четырех сил . Издательство Нова. п. 13. ISBN 1-59454-260-0 .
- ^ Жан Салансон; Стивен Лайл (2001). Справочник по механике сплошных сред: общие понятия, термоупругость . Спрингер. п. 9. ISBN 3-540-41443-6 .
- ^ Патрик Корниль (Ахлеш Лахтакиа, редактор) (1993). Очерки формальных аспектов электромагнитной теории . Всемирная научная. п. 149. ИСБН 981-02-0854-5 .
{{cite book}}:|author=имеет общее имя ( справка ) - ^ Нерлих, Грэм (1994). Что объясняет пространство-время: Метафизические очерки о пространстве и времени . Издательство Кембриджского университета. п. 64. ИСБН 0-521-45261-9 .
- ^ Джон Д. Нортон (1993). Общая ковариация и основы общей теории относительности: восемь десятилетий споров , Rep. Prog. Физ. , 56 , стр. 835-7.
- ^ Уильям Баркер; Роджер Хоу (2008). Непрерывная симметрия: от Евклида до Клейна . Американское математическое общество. п. 18 и далее. ISBN 978-0-8218-3900-3 .
- ^ Арлан Рамзи; Роберт Д. Рихтмайер (1995). Введение в гиперболическую геометрию . Спрингер. п. 11 . ISBN 0-387-94339-0 .
система координат аксиомы геометрии.
- ^ По словам Хокинга и Эллиса: «Многообразие - это пространство, локально похожее на евклидово пространство в том смысле, что оно может быть покрыто координатными участками. Эта структура позволяет определять дифференциацию, но не различает разные системы координат. Таким образом, единственные концепции определяемыми структурой многообразия, являются те, которые не зависят от выбора системы координат». Стивен В. Хокинг; Джордж Фрэнсис Рейнер Эллис (1973). Крупномасштабная структура пространства-времени . Издательство Кембриджского университета. п. 11. ISBN 0-521-09906-4 . Математическое определение: Связное хаусдорфово пространство M называется n -мерным многообразием, если каждая точка M содержится в открытом множестве, гомеоморфном открытому множеству в евклидовом n -мерном пространстве.
- ^ Сигэюки Морита; Теруко Нагасе; Кацуми Номидзу (2001). Геометрия дифференциальных форм . Книжный магазин Американского математического общества. п. 12 . ISBN 0-8218-1045-6 .
система координат аксиомы геометрии.
- ^ Гранино Артур Корн; Тереза М. Корн (2000). Математический справочник для ученых и инженеров: определения, теоремы и формулы для справки и обзора . Публикации Courier Dover. п. 169. ИСБН 0-486-41147-8 .
- ^ См . определение Энкарты . Архивировано 31 октября 2009 г.
- ^ Кацу Ямане (2004). Моделирование и создание движений человеческих фигур . Спрингер. стр. 12–13. ISBN 3-540-20317-6 .
- ^ Ахиллеус Папапетру (1974). Лекции по общей теории относительности . Спрингер. п. 5. ISBN 90-277-0540-2 .
- ^ Уилфорд Здуньковски; Андреас Ботт (2003). Динамика атмосферы . Издательство Кембриджского университета. п. 84. ИСБН 0-521-00666-Х .
- ^ А.И. Борисенко; ИП Тарапов; Ричард А. Сильверман (1979). Векторный и тензорный анализ с приложениями . Публикации Courier Dover. п. 86. ИСБН 0-486-63833-2 .
- ^ См. Арвинд Кумар; Шриш Барв (2003). Как и почему в базовой механике . Ориент Лонгман. п. 115. ИСБН 81-7371-420-7 .
- ^ Крис Доран; Энтони Ласенби (2003). Геометрическая алгебра для физиков . Издательство Кембриджского университета. п. §5.2.2, с. 133. ИСБН 978-0-521-71595-9 . .
- ^ Например, Мёллер утверждает: «Вместо декартовых координат мы, очевидно, можем с тем же успехом использовать общие криволинейные координаты для фиксации точек в физическом пространстве.… теперь мы введем общие «криволинейные» координаты x. я в четырехмерном пространстве…». К. Мёллер (1952). Теория относительности . Издательство Оксфордского университета. п. 222 и с. 233.
- ^ А. П. Лайтман; ВХ Пресс; РХ Цена; С. А. Теукольский (1975). Задача по теории относительности и гравитации . Издательство Принстонского университета. п. 15 . ISBN 0-691-08162-Х .
релятивистские общие координаты.
- ^ Ричард Л. Фабер (1983). Дифференциальная геометрия и теория относительности: введение . ЦРК Пресс. п. 211. ИСБН 0-8247-1749-Х .
- ^ Ричард Вольфсон (2003). Просто Эйнштейн . WW Norton & Co. p. 216. ИСБН 0-393-05154-4 .
- ^ См. Гвидо Рицци; Маттео Лука Руджеро (2003). Относительность во вращающихся системах отсчета . Спрингер. п. 33. ISBN 1-4020-1805-3 . .
- ^ Кэтрин Брэдинг; Елена Кастеллани (2003). Симметрии в физике: философские размышления . Издательство Кембриджского университета. п. 417. ИСБН 0-521-82137-1 .
- ^ Оливер Дэвис Джонс (2005). Аналитическая механика для теории относительности и квантовой механики . Издательство Оксфордского университета. Глава 16. ISBN 0-19-856726-Х .
- ^ Дональд Т. Гринвуд (1997). Классическая динамика (перепечатка издания 1977 года под ред. Прентис-Холла). Публикации Courier Dover. п. 313. ИСБН 0-486-69690-1 .
- ^ Мэтью А. Трамп; В. К. Шив (1999). Классическая релятивистская динамика многих тел . Спрингер. п. 99. ИСБН 0-7923-5737-Х .
- ^ Александр Соломонович Компанеец (2003). Теоретическая физика (перепечатка 2-го изд. 1962 г.). Публикации Courier Dover. п. 118. ИСБН 0-486-49532-9 .
- ^ М. Средницкий (2007). Квантовая теория поля . Издательство Кембриджского университета. Глава 4. ISBN 978-0-521-86449-7 .
- ^ Карло Ровелли (2004). Квантовая гравитация . Издательство Кембриджского университета. п. 98 и далее. ISBN 0-521-83733-2 .

![{\displaystyle \mathbf {r} =[x^{1},\ x^{2},\ \dots,\ x^{n}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7dd8270c4f5fa053e35aeab704c2d09b59e3275)




