Гравитационная сингулярность

Анимированная симуляция гравитационного линзирования , вызванного черной дырой Шварцшильда, проходящей на луче зрения в плоскости фоновой галактики. Вокруг и во время точного выравнивания ( сизигии ) наблюдается экстремальное линзирование света.

Гравитационная сингулярность , сингулярность пространства-времени или просто сингулярность — это состояние, при котором гравитация , по прогнозам, будет настолько интенсивной, что само пространство-время разрушится катастрофически. Таким образом, сингулярность по определению больше не является частью обычного пространства-времени и не может определяться «где» или «когда». Гравитационные сингулярности существуют на стыке общей теории относительности и квантовой механики ; следовательно, свойства особенности не могут быть описаны без устоявшейся теории квантовой гравитации . Попытка найти полное и точное определение сингулярностей в общей теории относительности, лучшей на данный момент теории гравитации, остается сложной проблемой. Сингулярность в общей теории относительности может быть определена тем, что скалярная инвариантная кривизна становится бесконечной. или, лучше, из- геодезической неполноты за .

Гравитационные сингулярности в основном рассматриваются в контексте общей теории относительности, где плотность стала бы бесконечной в центре черной дыры без поправок со стороны квантовой механики , а также в астрофизике и космологии как самое раннее состояние Вселенной во время Большого взрыва . Физики не пришли к единому мнению о том, что на самом деле происходит при экстремальных плотностях, предсказанных сингулярностями (в том числе в начале Большого взрыва).

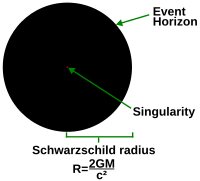
Общая теория относительности предсказывает, что любой объект, коллапсирующий за пределами определенной точки (для звезд это радиус Шварцшильда сингулярность (покрытая горизонтом событий ). ), образует черную дыру, внутри которой образуется Теоремы Пенроуза – Хокинга об особенностях определяют особенность, имеющую геодезические , которые не могут быть продолжены плавным образом . Окончание такой геодезической считается сингулярностью.

Современная теория утверждает, что начальное состояние Вселенной в начале Большого взрыва было сингулярностью. В этом случае Вселенная не коллапсировала в черную дыру, поскольку известные в настоящее время расчеты и пределы плотности гравитационного коллапса обычно основаны на объектах относительно постоянного размера, таких как звезды, и не обязательно применимы таким же образом к быстрому коллапсу. расширение пространства, такое как Большой взрыв. Ни общая теория относительности, ни квантовая механика в настоящее время не могут описать самые ранние моменты Большого взрыва . но в целом квантовая механика не позволяет частицам обитать в пространстве, меньшем, чем их длина волны .

Интерпретация

Многие теории в физике имеют математические особенности те или иные . Уравнения этих физических теорий предсказывают, что шар массы некоторой величины становится бесконечным или неограниченно увеличивается. Обычно это признак недостающего звена в теории, как, например, в случае ультрафиолетовой катастрофы , перенормировки и нестабильности атома водорода, предсказанных формулой Лармора .

В классических теориях поля, включая специальную теорию относительности, но не общую теорию относительности, можно сказать, что решение имеет сингулярность в определенной точке пространства-времени, где определенные физические свойства становятся плохо определенными, при этом пространство-время служит фоновым полем для обнаружения сингулярности. С другой стороны, сингулярность в общей теории относительности является более сложной, потому что само пространство-время становится плохо определенным, и сингулярность больше не является частью регулярного пространственно-временного многообразия. В общей теории относительности сингулярность не может быть определена посредством «где» или «когда».

Некоторые теории, такие как теория петлевой квантовой гравитации , предполагают, что сингулярности могут не существовать. Это справедливо и для таких классических единых теорий поля, как уравнения Эйнштейна–Максвелла–Дирака. Идею можно сформулировать в такой форме, что из-за эффектов квантовой гравитации существует минимальное расстояние, за пределами которого сила гравитации больше не продолжает увеличиваться по мере того, как расстояние между массами становится короче, или, альтернативно, волны взаимопроникающих частиц маскируют гравитационные эффекты. это будет ощущаться на расстоянии.

Руководствуясь такой философией петлевой квантовой гравитации, недавно было показано, что что подобные представления могут быть реализованы посредством некоторых элементарных конструкций, основанных на уточнении первой аксиомы геометрии, а именно понятия точки учитывая предписание Кляйна об учете расширения небольшого пятна, которое представляет или демонстрирует точку, это был программный вызов, который он назвал слиянием арифметики и геометрии. Программа Кляйн, согласно Борну, на самом деле представляла собой математический путь, позволяющий учитывать «естественную неопределенность во всех наблюдениях» при описании «физической ситуации» посредством «реальных величин».цифры».

Типы

Существует только один тип сингулярностей, каждый из которых имеет разные физические особенности, имеющие характеристики, соответствующие теориям, из которых они первоначально возникли, например, различные формы сингулярностей, конические и изогнутые . Также предполагалось, что они происходят без горизонтов событий, структур, которые отделяют один раздел пространства-времени от другого, в котором события не могут влиять за горизонт; их называют голыми.

Коническая

Коническая особенность возникает, когда существует точка, в которой предел некоторой инвариантной к диффеоморфизму величины не существует или бесконечен, и в этом случае пространство-время не является гладким в точке самого предела. Таким образом, вокруг этой точки пространство-время выглядит как конус , причем сингулярность находится на вершине конуса. Метрика может быть конечной везде, где система координат используется .

Примером такой конической сингулярности являются космическая струна и черная дыра Шварцшильда .

Кривизна

Простая иллюстрация невращающейся черной дыры и ее сингулярности.

Решения уравнений общей теории относительности или другой теории гравитации (например, супергравитации ) часто приводят к появлению точек, в которых метрика стремится к бесконечности. Однако многие из этих точек совершенно правильные , а бесконечности — всего лишь результат использования в этой точке неподходящей системы координат . Чтобы проверить, существует ли особенность в определенной точке, нужно проверить, становятся ли в этой точке инвариантные к диффеоморфизму величины (т.е. скаляры ) бесконечными. Такие величины одинаковы во всех системах координат, поэтому эти бесконечности не «уйдут» при изменении координат.

Примером может служить решение Шварцшильда , описывающее невращающуюся незаряженную черную дыру. часть метрики становится бесконечной В системах координат, удобных для работы в регионах, удаленных от черной дыры, на горизонте событий . Однако пространство-время на горизонте событий регулярно . Закономерность становится очевидной при переходе на другую систему координат (например, координаты Краскала ), где метрика совершенно гладкая . С другой стороны, в центре черной дыры, где метрика также становится бесконечной, решения предполагают существование сингулярности. Существование особенности можно проверить, заметив, что скаляр Кречмана представляет собой квадрат тензора Римана, т.е. $R_{\mu \nu \rho \sigma }R^{\mu \nu \rho \sigma }$, инвариантный к диффеоморфизму, бесконечен.

В то время как во вращающейся черной дыре сингулярность возникает в одной точке координат модели, называемой «точечной сингулярностью», во вращающейся черной дыре, также известной как черная дыра Керра , сингулярность возникает в кольце (круговом линия), известная как « кольцевая особенность ». Такая сингулярность теоретически также может стать червоточиной .

В более общем смысле, пространство-время считается сингулярным, если оно геодезически неполно , что означает, что существуют свободно падающие частицы, движение которых не может быть определено за пределами конечного времени, поскольку они находятся после точки достижения сингулярности. Например, любой наблюдатель внутри горизонта событий невращающейся черной дыры упадет в ее центр за конечный период времени. Классическая версия Большого взрыва космологической модели Вселенной ( содержит причинную сингулярность в начале времени =0 ) t , где все времяподобные геодезические не имеют продолжения в прошлое. Экстраполяция назад к этому гипотетическому времени 0 приводит к появлению Вселенной со всеми пространственными измерениями нулевого размера, бесконечной плотностью, бесконечной температурой и бесконечной кривизной пространства-времени.

Голая сингулярность

Основная статья: Голая сингулярность

До начала 1990-х годов широко распространено мнение, что общая теория относительности скрывает каждую сингулярность за горизонтом событий , делая невозможными голые сингулярности. Это называется гипотезой космической цензуры . Однако в 1991 году физики Стюарт Шапиро и Сол Теукольский выполнили компьютерное моделирование вращающейся плоскости пыли, которое показало, что общая теория относительности может учитывать «голые» сингулярности. Как на самом деле будут выглядеть эти объекты в такой модели, неизвестно. Неизвестно также, будут ли по-прежнему возникать сингулярности, если убрать упрощающие допущения, использованные при моделировании. Однако предполагается, что свет, попадающий в сингулярность, аналогичным образом обрывает геодезические линии, в результате чего голая сингулярность будет выглядеть как черная дыра.

Исчезающие горизонты событий существуют в метрике Керра , которая представляет собой вращающуюся черную дыру в вакууме, если угловой момент ( $J$) достаточно высока. Преобразуя метрику Керра в координаты Бойера – Линдквиста , можно показать что координата (которая не является радиусом) горизонта событий равна $r_{\pm }=\mu \pm \left(\mu ^{2}-a^{2}\right)^{1/2}$, где $\mu =GM/c^{2}$, и $a=J/Mc$. В данном случае «горизонты событий исчезают» означает, что решения сложны для $r_{\pm }$, или $\mu ^{2}<a^{2}$. Однако это соответствует случаю, когда $J$ превышает $GM^{2}/c$ (или в планковских единицах , $J>M^{2}$) ; т.е. спин превышает то, что обычно считается верхним пределом его физически возможных значений.

Аналогичным образом, исчезающие горизонты событий также можно увидеть в геометрии Рейсснера – Нордстрема заряженной черной дыры, если заряд ( $Q$) достаточно высока. В этом показателе можно показать что особенности возникают при $r_{\pm }=\mu \pm \left(\mu ^{2}-q^{2}\right)^{1/2}$, где $\mu =GM/c^{2}$, и $q^{2}=GQ^{2}/\left(4\pi \epsilon _{0}c^{4}\right)$. Из трех возможных случаев относительных значений $\mu$ и $q$, случай, когда $\mu ^{2}<q^{2}$ вызывает оба $r_{\pm }$ быть сложным. Это означает, что метрика регулярна для всех положительных значений $r$или, другими словами, сингулярность не имеет горизонта событий. Однако это соответствует случаю, когда $Q/{\sqrt {4\pi \epsilon _{0}}}$ превышает $M{\sqrt {G}}$ (или в планковских единицах, $Q>M$) ; т.е. заряд превышает то, что обычно считается верхним пределом его физически возможных значений. Кроме того, не ожидается, что настоящие астрофизические черные дыры будут обладать каким-либо заметным зарядом.

Черная дыра, обладающая самой низкой $M$ ценность, соответствующая его $J$ и $Q$ значения и пределы, указанные выше; то есть тот, кто находится на грани потери горизонта событий, называется экстремальным .

Энтропия

Дополнительная информация: Черная дыра , излучение Хокинга и энтропия.

До того, как Стивен Хокинг придумал концепцию излучения Хокинга , вопрос о том, обладают ли черные дыры энтропией, избегался. Однако эта концепция демонстрирует, что черные дыры излучают энергию, которая сохраняет энтропию и решает проблемы несовместимости со вторым законом термодинамики . Однако энтропия подразумевает тепло и, следовательно, температуру. Потеря энергии также означает, что черные дыры не существуют вечно, а скорее испаряются или медленно распадаются. Температура черной дыры обратно пропорциональна массе . Все известные кандидаты в черные дыры настолько велики, что их температура намного ниже температуры космического фонового излучения, а это означает, что они будут получать чистую энергию, поглощая это излучение. Они не могут начать терять энергию в сети, пока фоновая температура не упадет ниже их собственной температуры. Это произойдет при космологическом красном смещении , превышающем один миллион, а не тысячу или около того с момента образования фонового излучения.

См. также

• 0-мерная сингулярность: магнитный монополь
• Одномерная сингулярность: космическая струна
• Двумерная сингулярность: доменная стенка
• Фаззбол (теория струн)
• Теоремы Пенроуза – Хокинга об особенностях
• Белая дыра
• БКЛ сингулярность
• Начальная сингулярность

Библиография

• Эрман, Джон (1995). Удары, хруст, хныканье и визги: сингулярности и акаузалии в релятивистском пространстве-времени . Издательство Оксфордского университета. ISBN  019509591X .
• Джоши, Панкадж С. (2007). Гравитационный коллапс и сингулярности пространства-времени . Нью-Йорк: Издательство Кембриджского университета. ISBN  9781107405363 .
• Миснер, Чарльз В .; Торн, Кип ; Уилер, Джон Арчибальд (1973). Гравитация . У. Х. Фриман . ISBN  0-7167-0344-0 . §31.2 Несингулярность гравитационного радиуса и последующие разделы; §34 Глобальные методы, горизонты и теоремы о сингулярности
• Уолд, Роберт М. (1984). Общая теория относительности . Издательство Чикагского университета . ISBN  0-226-87033-2 .

• Хокинг, Юго-Запад ; Пенроуз, Р. (1970), «Особенности гравитационного коллапса и космологии», Proc. Р. Сок. А , 314 (1519): 529–548, Бибкод : 1970RSPSA.314..529H , doi : 10.1098/rspa.1970.0021 (Доступ свободный.)
• Шапиро, Стюарт Л.; Теукольский, Саул А. (1991). «Формирование голых сингулярностей: нарушение космической цензуры» (PDF) . Письма о физических отзывах . 66 (8): 994–997. Бибкод : 1991PhRvL..66..994S . doi : 10.1103/PhysRevLett.66.994 . ПМИД   10043968 . S2CID   7830407 .
• Пенроуз, Роджер (1996). «Чандрасекар, черные дыры и особенности» . ias.ac.in. ​
• Пенроуз, Роджер (1999). «Вопрос космической цензуры» . ias.ac.in. ​
• Сингх, Т.П. (1999) «Гравитационный коллапс, черные дыры и обнаженные особенности» . ias.ac.in. ​

Дальнейшее чтение

• Элегантная вселенная Брайана Грина . Эта книга представляет собой введение в теорию струн для непрофессионала , хотя некоторые из высказанных взглядов уже устарели. Использование им общих терминов и примеры по всему тексту помогают непрофессионалу понять основы теории струн.