Спагеттификация

В астрофизике спагеттификация ) называемая эффектом лапши ( иногда [1] — это вертикальное растяжение и горизонтальное сжатие объектов в длинные тонкие формы (похожие на спагетти ) в очень сильном неоднородном гравитационном поле . Это вызвано чрезвычайными приливными силами . В самых крайних случаях вблизи черной дыры растяжение и сжатие настолько сильны, что ни один объект не может им противостоять. В пределах небольшой области горизонтальное сжатие уравновешивает вертикальное растяжение, так что спагеттируемый небольшой объект не испытывает общего изменения в объеме.
Стивен Хокинг описал полет вымышленного астронавта черной дыры , который, проходя в пределах горизонта событий , «растягивается, как спагетти» гравитационным градиентом (разницей в гравитационных силах) с головы до ног. [2] Причина, по которой это происходит, заключается в том, что гравитационная сила, действующая на сингулярность, будет намного сильнее на одном конце тела, чем на другом. Если бы кто-то упал в черную дыру ногами вперед, гравитация в ногах была бы намного сильнее, чем в голове, в результате чего человек растянулся бы по вертикали. При этом правая часть тела будет тянуться влево, а левая — вправо, сжимая человека по горизонтали. [3] Однако термин «спагеттификация» появился задолго до этого. [4] Спагеттификация звезды была впервые получена в 2018 году исследователями, наблюдавшими за парой сталкивающихся галактик примерно в 150 миллионах световых лет от Земли. [5]
Простой пример
[ редактировать ]
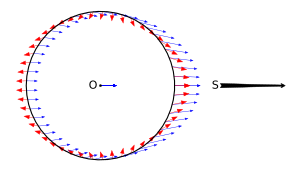
В этом примере четыре отдельных объекта находятся в пространстве над планетой и расположены в виде ромба. Четыре объекта следуют линиям гравитоэлектрического поля . [6] направлена к центру небесного тела. В соответствии с законом обратных квадратов самый нижний из четырех объектов испытывает наибольшее гравитационное ускорение, так что все образование вытягивается в линию.
Эти четыре объекта являются соединенными частями более крупного объекта. Твердое тело будет сопротивляться деформации, и по мере деформации тела развиваются внутренние силы упругости, чтобы уравновесить приливные силы и таким образом достичь механического равновесия . Если приливные силы слишком велики, тело может поддаться и пластически течь до того, как приливные силы смогут уравновеситься, или сломаться, образуя либо нить, либо вертикальную линию из разбитых частей.
Примеры слабых и сильных приливных сил
[ редактировать ]В этом разделе есть несколько проблем. Пожалуйста, помогите улучшить его или обсудите эти проблемы на странице обсуждения . ( Узнайте, как и когда удалять эти шаблонные сообщения )
|
В поле силы тяжести, обусловленном точечной массой или сферической массой, для однородного стержня, ориентированного в направлении силы тяжести, растягивающая сила в центре находится путем интегрирования приливной силы от центра к одному из концов. Это дает F = мкм лм / 4 года 3 , где μ — стандартный гравитационный параметр массивного тела, l — длина стержня, m — масса стержня, а r — расстояние до массивного тела. Для неоднородных объектов растягивающая сила меньше, если больше массы находится вблизи центра, и в два раза больше, если больше массы находится на концах. Кроме того, к центру действует горизонтальная сила сжатия.
Для массивных тел, имеющих поверхность, растягивающая сила наибольшая вблизи поверхности, и это максимальное значение зависит только от объекта и средней плотности массивного тела (пока объект мал по отношению к массивному телу). Например, для стержня массой 1 кг и длиной 1 м и массивного тела средней плотности Земли эта максимальная растягивающая сила, обусловленная приливной силой, составляет всего 0,4 мкН.
Из-за высокой плотности приливная сила у поверхности белого карлика гораздо сильнее, вызывая в примере максимальную растягивающую силу до 0,24 Н. Вблизи нейтронной звезды приливные силы снова гораздо сильнее: если стержень имеет предел прочности 10 000 Н и падает вертикально на нейтронную звезду массой 2,1 солнечной массы, если не считать того, что она расплавится, она сломается на расстоянии 190 км от центра, значительно над поверхностью (нейтронная звезда обычно имеет радиус всего около 12 км). [примечание 1]
В предыдущем случае объекты фактически были бы уничтожены, а люди погибли бы от жары, а не от приливных сил, но вблизи черной дыры (при условии, что поблизости нет материи) объекты фактически были бы уничтожены, а люди погибли бы от приливных сил, потому что излучения нет (кроме теоретического излучения Хокинга). Более того, у черной дыры нет поверхности, которая могла бы остановить падение. Таким образом, падающий объект растягивается в тонкую полоску материи.
Внутри или за пределами горизонта событий
[ редактировать ]
Момент, когда приливные силы уничтожат объект или убьют человека, будет зависеть от размера черной дыры. Для сверхмассивной черной дыры , такой как обнаруженная в центре галактики, эта точка лежит в пределах горизонта событий , поэтому астронавт может пересечь горизонт событий, не заметив никакого сдавливания и притяжения, хотя это остается лишь вопросом времени, как и попадание внутрь горизонт событий, падение к центру неизбежно. [8] Для небольших черных дыр, чей радиус Шварцшильда намного ближе к сингулярности , приливные силы убьют еще до того, как астронавт достигнет горизонта событий. [9] [10] Например, для черной дыры массой 10 масс Солнца [примечание 2] вышеупомянутый стержень ломается на расстоянии 320 км, что далеко за пределами радиуса Шварцшильда в 30 км. Для сверхмассивной черной дыры массой 10 000 масс Солнца она разрушится на расстоянии 3 200 км, что находится в пределах радиуса Шварцшильда в 30 000 км.
Примечания
[ редактировать ]- ^ 8-метровый стержень той же силы и массой 8 кг ломается на расстоянии в 4 раза большем. [ нужна ссылка ]
- ^ Самая маленькая непервичная черная дыра , которая может образоваться в результате естественных процессов, по оценкам, имеет массу в 3–4 раза больше массы Солнца. [11]
Ссылки
[ редактировать ]- Встроенные цитаты
- ^ Уилер, Дж. Крейг (2007), Космические катастрофы: взрывающиеся звезды, черные дыры и составление карты Вселенной (2-е изд.), Cambridge University Press , стр. 182, ISBN 978-0-521-85714-7
- ^ Хокинг, Стивен (1988). Краткая история времени . Издательская группа Bantam Dell. п. 256. ИСБН 978-0-553-10953-5 .
- ^ Астрономия . ОпенСтакс. 2016. с. 862. ИСБН 978-1938168284 .
- ^ Колдер, Найджел (1977). Ключ к Вселенной: доклад о новой физике . Викинг Пресс . п. 143. ИСБН 978-0-67041270-9 . Проверено 10 июля 2022 г. Опубликовано вместе с BBC документальным фильмом «Ключ к Вселенной» .
- ^ «Астрономы видят отдаленное извержение, поскольку черная дыра уничтожает звезду» (пресс-релиз). Национальная радиоастрономическая обсерватория. Физика.орг. 14 июня 2018 г. Проверено 15 июня 2018 г.
- ^ Торн, Кип С. (1988). «Гравитомагнетизм, струи в квазарах и Стэнфордский эксперимент с гироскопом» (PDF) . В Фэрбанке, JD; Дивер-младший, бакалавр наук; Эверитт, CF; Мисельсон, П.Ф. (ред.). Около нуля: новые рубежи физики . Нью-Йорк : WH Freeman and Company . стр. 3, 4 (575, 576).
что любое вращающееся сферическое тело (например, Солнце или Земля) будет окружено радиальным гравитоэлектрическим (ньютоновским) полем g и диполярным гравитомагнитным полем H. Из нашего электродинамического опыта мы можем сразу заключить , Гравитоэлектрический монопольный момент — это масса тела М; гравитомагнитный дипольный момент — это его спиновый угловой момент S.
- ^ «Вращающаяся черная дыра, поглощающая звезду, объясняет сверхяркое событие – телескопы ESO помогают по-новому интерпретировать яркий взрыв» . www.eso.org . Проверено 15 декабря 2016 г.
- ^ Хоули, Джон Ф.; Холкомб, Кэтрин А. (2005). Основы современной космологии (иллюстрированное изд.). Издательство Оксфордского университета. п. 253. ИСБН 978-0-19-853096-1 . Выдержка со страницы 253
- ^ Хобсон, Майкл Пол; Эфстатиу, Джордж; Ласенби, Энтони Н. (2006). «11. Шварцшильдовские черные дыры» . Общая теория относительности: введение для физиков . Издательство Кембриджского университета. п. 265. ИСБН 0-521-82951-8 .
- ^ Катнер, Марк Лесли (2003). «8. Общая теория относительности» . Астрономия: физическая перспектива (2-е изд.). Издательство Кембриджского университета. п. 150. ИСБН 0-521-52927-1 .
- ^ Томпсон, штат Техас; Кочанек, CS; Станек, Казахстан; и др. (2019). «Невзаимодействующая двойная система черная дыра малой массы – звезда-гигант». Наука . 366 (6465): 637–640. arXiv : 1806.02751 . Бибкод : 2019Sci...366..637T . дои : 10.1126/science.aau4005 . ПМИД 31672898 . S2CID 207815062 .
- Общие ссылки
- Мелия, Фульвио (2003). Черная дыра в центре нашей Галактики . Издательство Принстонского университета . ISBN 0-691-09505-1 .
