Приливная сила

Рисунок 1: Приливное взаимодействие между спиральной галактикой с перемычкой NGC 169 и меньшим спутником.

Приливная сила или сила, порождающая прилив, представляет собой гравитационный эффект, который растягивает тело вдоль линии к центру масс другого тела и от него из-за пространственных изменений силы гравитационного поля другого тела. Он отвечает за приливы и связанные с ними явления, в том числе твердоземные приливы , приливные блокировки , разрыв небесных тел и образование кольцевых систем в пределах предела Роша , а в крайних случаях — спагеттификацию объектов. Оно возникает потому, что гравитационное поле, действующее на одно тело со стороны другого, не является постоянным в его частях: ближняя сторона притягивается сильнее, чем дальняя. Разница положительна на ближней стороне и отрицательна на дальней стороне, что приводит к растяжению тела. Таким образом, приливная сила также известна как дифференциальная сила, остаточная сила или вторичный эффект гравитационного поля.

В небесной механике выражение приливная сила может относиться к ситуации, в которой тело или материал (например, приливная вода) находится в основном под гравитационным воздействием второго тела (например, Земли), но также возмущается гравитационное воздействие третьего тела (например, Луны). Возмущающую силу в таких случаях иногда называют приливной силой. (например, возмущающая сила на Луне ): это разница между силой, действующей третьим телом на второе, и силой, действующей третьим телом на первое.

Было также показано, что приливные силы фундаментально связаны с гравитационными волнами .

Объяснение

гравитационное поле Луны Рисунок 2: Показано красным, остаточное на поверхности Земли известно (наряду с другим, более слабым дифференциальным эффектом, обусловленным Солнцем) как сила, порождающая приливы . Это основной механизм, вызывающий приливные действия, объясняющий два одновременных приливных выступа.

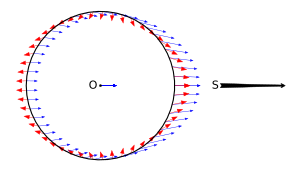
Вращение Земли также является причиной возникновения двух приливов в день в одном и том же месте. На этом рисунке Земля представляет собой центральный черный круг, а Луна находится далеко справа. На нем показано как приливное поле (толстые красные стрелки), так и гравитационное поле (тонкие синие стрелки), действующие на поверхность и центр Земли (метка O) со стороны Луны (метка S). Направление наружу стрелок справа и слева от Земли указывает на то, где Луна находится в зените или в надире .

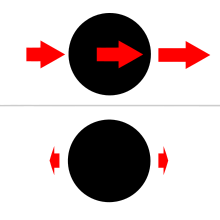
Когда на тело (тело 1) действует сила тяжести другого тела (тела 2), поле на теле 1 может значительно различаться между стороной тела, обращенной к телу 2, и стороной, обращенной от тела 2. На рисунке 2 показано дифференциальная сила тяжести, действующая на сферическое тело (тело 1), действующая на другое тело (тело 2).

Эти приливные силы вызывают напряжения обоих тел и могут их деформировать или даже, в крайних случаях, разорвать одно или другое на части. Предел Роша — это расстояние от планеты, на котором приливные эффекты могут привести к распаду объекта, поскольку дифференциальная сила гравитации планеты преодолевает притяжение частей объекта друг к другу. Эти деформации не возникли бы, если бы гравитационное поле было однородным, потому что однородное поле заставляет все тело ускоряться только в одном направлении и с одинаковой скоростью.

Размер и расстояние

Отношение размера астрономического тела к его расстоянию от другого тела сильно влияет на величину приливной силы. Приливная сила, действующая на астрономическое тело, например Землю, прямо пропорциональна диаметру Земли и обратно пропорциональна кубу расстояния от другого тела, создающего гравитационное притяжение, например Луны или Солнца. Приливное воздействие на ванны, бассейны, озера и другие небольшие водоемы незначительно.

Рисунок 3. График, показывающий, как гравитационное притяжение падает с увеличением расстояния от тела.

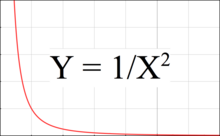
Рисунок 3 представляет собой график, показывающий, как сила гравитации уменьшается с расстоянием. На этом графике сила притяжения уменьшается пропорционально квадрату расстояния ( Y = 1/ X ² ), а наклон ( Y ′ = −2/ X ³ ) обратно пропорциональна кубу расстояния.

Приливная сила соответствует разнице Y между двумя точками на графике: одна точка находится на ближней стороне тела, а другая - на дальней стороне. Приливная сила становится больше, когда две точки находятся либо дальше друг от друга, либо когда они находятся левее на графике, то есть ближе к притягивающему телу.

Например, хотя Солнце имеет более сильное общее гравитационное притяжение к Земле, Луна создает большую приливную выпуклость, потому что Луна находится ближе. Эта разница связана с тем, как гравитация ослабевает с расстоянием: более близкая близость Луны приводит к более резкому снижению ее гравитационного притяжения при движении по Земле (по сравнению с очень постепенным снижением Солнца с его огромного расстояния). Этот более крутой градиент притяжения Луны приводит к большей разнице в силе между ближней и дальней сторонами Земли, что и создает большую приливную выпуклость.

Гравитационное притяжение обратно пропорционально квадрату расстояния от источника. Притяжение будет сильнее на стороне тела, обращенной к источнику, и слабее на стороне, противоположной источнику. Приливная сила пропорциональна разнице.

Солнце, Земля и Луна

Земля в 81 раз массивнее Луны, а радиус Земли примерно в 4 раза больше Луны. В результате на одном и том же расстоянии приливная сила Земли у поверхности Луны примерно в 20 раз сильнее, чем у Луны у поверхности Земли.

Гравитационное тело, вызывающее приливную силу		Тело, подверженное приливной силе			Приливное ускорение
Тело	Масса ( $m$)	Тело	Радиус ( $r$)	Расстояние ( $d$)	$Gm~{\frac {2r}{d^{3}}}$
Солнце	1.99 × 10 30 кг	Земля	6.37 × 10 6 м	1.50 × 10 11 м	5.05 × 10 −7  m⋅s −2
Луна	7.34 × 10 22 кг	Земля	6.37 × 10 6 м	3.84 × 10 8 м	1.10 × 10 −6  m⋅s −2
Земля	5.97 × 10 24 кг	Луна	1.74 × 10 6 м	3.84 × 10 8 м	2.44 × 10 −5  m⋅s −2
G — гравитационная постоянная = 6,674 × 10. −11 м 3 ⋅kg −1 ⋅s −2

Эффекты

Рисунок 4. Сатурна Кольца находятся внутри орбит его главных спутников. Приливные силы противодействуют гравитационному слиянию материала колец с образованием спутников.

В случае бесконечно малого упругого шара действие приливной силы заключается в искажении формы тела без какого-либо изменения объема. Сфера становится эллипсоидом с двумя выпуклостями, направленными к другому телу и от него. Более крупные объекты искажаются в яйцевидную форму и слегка сжимаются, что и происходит с земными океанами под действием Луны. Все части Земли подвержены гравитационным силам Луны, в результате чего вода в океанах перераспределяется, образуя выпуклости по бокам вблизи Луны и вдали от Луны.

Когда тело вращается под действием приливных сил, внутреннее трение приводит к постепенному рассеиванию его кинетической энергии вращения в виде тепла. В случае Земли и Луны потеря кинетической энергии вращения приводит к выигрышу примерно в 2 миллисекунды за столетие. Если тело находится достаточно близко к своему основному телу, это может привести к вращению, которое приливно привязано к орбитальному движению, как в случае с Луной Земли. Приливное нагревание вызывает драматические вулканические последствия на спутнике Юпитера Ио . Напряжения, вызванные приливными силами, также вызывают регулярные ежемесячные лунные землетрясения на Луне.

Приливные силы способствуют возникновению океанских течений, которые смягчают глобальные температуры, перенося тепловую энергию к полюсам. Было высказано предположение, что изменения приливных сил коррелируют с прохладными периодами глобальных температурных рекордов с интервалом от 6 до 10 лет. и что гармонические изменения ритма приливных воздействий могут способствовать тысячелетним изменениям климата. На сегодняшний день не обнаружено сильной связи с изменениями климата в тысячелетии.

Рисунок 5: Комета Шумейкера-Леви 9 в 1994 году после распада под воздействием приливных сил Юпитера во время предыдущего прохода в 1992 году.

Приливные эффекты становятся особенно выраженными вблизи небольших тел большой массы, таких как нейтронные звезды или черные дыры , где они ответственны за « спагеттификацию » падающей материи. Приливные силы создают океанический прилив океанов Земли , где притягивающими телами являются Луна и, в меньшей степени, Солнце . Приливные силы также ответственны за приливную блокировку , приливное ускорение и приливный нагрев. Приливы также могут вызывать сейсмичность .

Создавая проводящие жидкости внутри Земли, приливные силы также влияют на магнитное поле Земли .

Рисунок 6: Эта симуляция показывает, как звезда разрывается на части гравитационными приливами сверхмассивной черной дыры .

Формулировка

Рисунок 7: Приливная сила ответственна за слияние галактической пары MRK 1034 .

Рисунок 8: График приливных сил. На верхнем рисунке показано гравитационное поле тела справа (не показано); нижний показывает их остаточную гравитацию после вычитания поля в центре сферы; это приливная сила. Для наглядности верхние стрелки можно принять равными 1 Н, 2 Н и 3 Н (слева направо); результирующие нижние стрелки будут равны соответственно -1 Н (отрицательное значение, т.е. повернуто на 180 градусов), 0 Н (невидимое) и 1 Н. Более подробную версию см. на рисунке 2.

Для данного (внешне генерируемого) гравитационного поля приливное ускорение в точке относительно тела получается векторным вычитанием гравитационного ускорения в центре тела (обусловленного данным внешне генерируемым полем) из гравитационного ускорения ( за счет того же поля) в данной точке. Соответственно, термин « приливная сила» используется для описания сил, возникающих вследствие приливного ускорения. Заметим, что для этих целей рассматривается только внешнее гравитационное поле; гравитационное поле тела (как показано на рисунке) не имеет значения. (Другими словами, сравнение происходит с условиями в данной точке такими, какими они были бы, если бы не было внешнего поля, действующего неодинаково в данной точке и в центре тела отсчета. Внешне созданным полем обычно является поле, создаваемое возмущающее третье тело, часто Солнце или Луна в частых примерах точек на поверхности Земли или над ней в геоцентрической системе отсчета.)

Приливное ускорение не требует вращения или вращения тел; например, тело может свободно падать по прямой под действием гравитационного поля, при этом все еще находясь под влиянием (меняющегося) приливного ускорения.

По закону всемирного тяготения Ньютона и законам движения тело массы m , находящееся на расстоянии R от центра сферы массы M, испытывает силу ${\vec {F}}_{g}$,

${\vec {F}}_{g}=-{\hat {r}}~G~{\frac {Mm}{R^{2}}}$

эквивалент ускорения ${\vec {a}}_{g}$,

${\vec {a}}_{g}=-{\hat {r}}~G~{\frac {M}{R^{2}}}$

где ${\hat {r}}$ — единичный вектор , направленный от тела M к телу m (здесь ускорение от m в сторону M имеет отрицательный знак).

Рассмотрим теперь ускорение сферы массы M, испытываемое частицей вблизи тела массы m . Если R — это расстояние от центра M до центра m , то пусть ∆ r — это (относительно небольшое) расстояние частицы от центра тела массы m . Для простоты расстояния сначала рассматриваются только в направлении, направленном к сфере массы M или от нее . Если тело массы m само является сферой радиуса ∆r , то рассматриваемая новая частица может располагаться на его поверхности на расстоянии ( R ± ∆r ) от центра сферы массы M , а ∆r может считать положительным, если расстояние частицы от M больше, чем R . Оставляя в стороне любое гравитационное ускорение, которое может испытывать частица по направлению к m из-за массы m собственной , мы имеем ускорение частицы, вызванное силой гравитации по направлению к M, как:

${\vec {a}}_{g}=-{\hat {r}}~G~{\frac {M}{(R\pm \Delta r)^{2}}}$

Вытаскивание буквы Р. ² член из знаменателя дает:

${\vec {a}}_{g}=-{\hat {r}}~G~{\frac {M}{R^{2}}}~{\frac {1}{\left(1\pm {\frac {\Delta r}{R}}\right)^{2}}}$

Серия Маклоренов . $1/(1\pm x)^{2}$ является $1\mp 2x+3x^{2}\mp \cdots$ что дает разложение в ряд:

${\vec {a}}_{g}=-{\hat {r}}~G~{\frac {M}{R^{2}}}\pm {\hat {r}}~G~{\frac {2M}{R^{2}}}~{\frac {\Delta r}{R}}+\cdots$

Первый член — это гравитационное ускорение, вызванное силой M в центре тела сравнения. $m$, то есть в точке, где $\Delta r$ равен нулю. Этот член не влияет на наблюдаемое ускорение частиц на поверхности m, относительно M поскольку m (и все на его поверхности) находится в свободном падении. Когда сила, действующая на дальнюю частицу, вычитается из силы, действующей на ближнюю частицу, этот первый член сокращается, как и все остальные члены четного порядка. Остальные (остаточные) члены представляют собой разницу, упомянутую выше, и являются членами приливной силы (ускорения). Когда ∆ r мало по сравнению с R , члены после первого остаточного члена очень малы, и ими можно пренебречь, что дает приблизительное приливное ускорение ${\vec {a}}_{t,{\text{axial}}}$ для рассматриваемых расстояний ∆r вдоль оси, соединяющей центры m и M :

${\vec {a}}_{t,{\text{axial}}}\approx \pm {\hat {r}}~2\Delta r~G~{\frac {M}{R^{3}}}$

При таком расчете для случая, когда ∆ r — расстояние вдоль оси, соединяющей центры m и M , ${\vec {a}}_{t}$ направлена ​​наружу из к центру m (где ∆ r равно нулю).

Приливные ускорения также можно рассчитать вдали от оси, соединяющей тела m и M , что требует векторного расчета. В плоскости, перпендикулярной этой оси, приливное ускорение направлено внутрь (к центру, где ∆ r равно нулю), и его величина равна ${\textstyle {\frac {1}{2}}\left|{\vec {a}}_{t,{\text{axial}}}\right|}$ в линейном приближении, как на рисунке 2.

Приливные ускорения на поверхности планет Солнечной системы обычно очень малы. Например, лунное приливное ускорение у поверхности Земли вдоль оси Луна-Земля составляет около 1,1 × 10 ⁻⁷  g , а солнечное приливное ускорение у поверхности Земли вдоль оси Солнце–Земля составляет около 0,52 × 10 ⁻⁷  g , где g — ускорение свободного падения на поверхности Земли. Следовательно, приливная сила (ускорение), вызываемая Солнцем, составляет около 45% от силы, создаваемой Луной. Солнечное приливное ускорение на поверхности Земли было впервые дано Ньютоном в « Началах» .

См. также

• Амфидромная точка
• Разрушенная планета
• Галактический прилив
• Приливный резонанс
• Приливная зачистка
• Приливный тензор
• Кривизна пространства-времени

Внешние ссылки

• Анализ и прогноз приливов: GeoTide
• «Гравитационные приливы» , Дж. Кристофер Михос из Университета Кейс Вестерн Резерв
• Аудио: Каин/Гей – Астрономия, приливные силы – июль 2007 г.
• Грей, Меган; Меррифилд, Майкл. «Приливные силы» . Шестьдесят символов . Брэди Харан из Ноттингемского университета .
• Пау Амаро Сеоане. «Звездные столкновения: приливное разрушение звезды массивной черной дырой» . Проверено 28 декабря 2018 г.
• «Мифы о гравитации и приливах» , Миколай Савицкий из Колледжа Джона А. Логана и Университета Колорадо.
• Приливные заблуждения Дональда Э. Симанека
• Приливы и центробежная сила Паоло Сиртоли